基于果蝇优化支持向量机的风机故障诊断研究

洪文鹏 廖明俊/东北电力大学能源与动力工程学院

0 引言

离心式风机是火电厂中的主要辅助设备[1-2]，也是火电厂中厂用电耗量较大的设备，其地位很重要，但常常由于出现各种不同形式的振动故障而影响其正常工作[3]，有时会发生严重的事故，造成重大的经济损失。

由于支持向量机中的核函数的参数选择问题直接影响到支持向量机模型的推广能力，所以，为了提高离心式风机故障分类的精确性，本文基于流形学习原理，研究应用局部线性嵌入法对汽轮发电机组振动信号进行有效降维的方法，从而实现在复杂的噪声信号中提取有效的识别机组轴系振动故障的特征信息[4-5]。尝试支持向量机(Support vector machine，SVM)[6]进行模式识别,同时运用果蝇算法(Fruit Fly Optimization Algorithm，FOA)[7]对支持向量机所选择的核函数进行参数优化。

因此FOA-SVM故障诊断模型可以很好地解决参数优化问题同时能提高诊断的速度。运用FOA-SVM 模型对故障进行了诊断，同时与粒子群优化[8]最小二乘支持向量机和蚁群算法[9-10]优化最小二乘支持向量机的诊断进行了比较。

1 流形学习原理和局部线性嵌入法

1.1 流形学习原理

1.2 局部线性嵌入法

自流形学习原理提出以后，出现了各种流形学习方法。一种典型的流形学习方法是局部线性嵌入法(Locally Linear Embedding,LLE)。LLE法是一种典型的非线性降维方法，它主要是从局部入手，将非线性数据分割成具有局部线性结构的数据，通过欧氏距离以局部线形来保持整体拓扑结构，因此，对非线性数据有很好的降维效果。

LLE法的主要过程如下[13]：

1）寻找每个样本点xi的k 个近邻。定义样本集矩阵X={x1,x2,…,xN}中样本点xi与xj的距离dij为

式中，通常取p=2，即采用欧氏距离。根据式(1)计算得到样本点xi的k个距离最近的点作为gj的k个近邻点。

2）计算样本点局部重构的权值矩阵wi。为此，首先定义误差函数

式中：gj(j=1,2,…,k)为xi的k 个近邻点；wij为xi与gj之间的权值系数，且满足

将式(3)代入式(2)得到

3）将所有样本点映射嵌入到低维空间中。映射嵌入满足

式中：φ（Y）是损失函数；yi是xi的输出向量；hj(j=1，2，…，k)是yi的k个近邻点，且满足

式中：I 为d×d 的单位矩阵。这里，wij(i=1,2,…,N)可以存储在N×N的稀疏矩阵W中。当{xj}是{xi}的近邻点时，Wij=wij；否则Wij=0。用Wi表示W矩阵的第i列，Ii表示单位矩阵的第i列，Y表示输出向量，即Y=[y1,y2,…,yN]，则式（5）可写为

为使损失函数L（Y）最小，则

将M 的特征值按从小到大顺序排列，Y 取M的最小d 个非零特征值所对应的特征向量。一般地，M 的第一个特征值几乎等于零。因此，取2～(d+1)个特征值所对应的特征向量作为低维嵌入Y。

由上述过程可以看出，LLE法的主要参数是近邻数k和嵌入维数d。

2 SVM算法基本原理及果蝇算法

2.1 SVM算法基本原理

支持向量的基本思想是：通过非线性映射函数把数据样本映射到高维特征空间，再在高维特征空间中求得最优分类面来分离训练样本点，使得训练样本点与最优分离面距离最大化。

给定样本集T={xi,yi│i=1,2,…,m}，其中xi∈Rn表示输入矢量；yi∈{+1,-1}表示对应的期望输出矢量；m 为样本数。通过非线性映射函数，将输入数据从原空间映射到高维特征空间，在高维特征空间中构造最优分类超平面

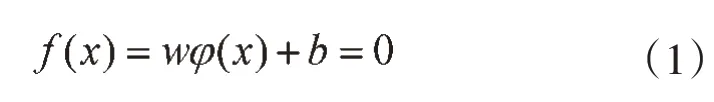
式中：w 表示权值矢量；b 为阈值。w 和b 确定了分类面的位置。分类面必须满足以下约束：

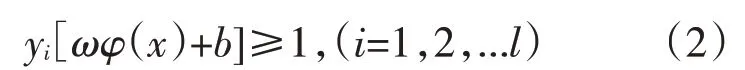
引入松弛变量ξi，ξi用于衡量实际指标值yi与支持向量机输出之间的距离。数据分离面的优化问题转变为以下优化问题：

式中：C 为惩罚参数，用于实现对错分样本惩罚程度的控制。

引入Lagrangian 乘子αi，上述优化问题转化为二次规划的优化问题：小二乘线性系统，降低了计算复杂性，提高了求解速度。

根据KKT条件，优化系数必须满足：

求解上述问题，于是得到最优分类函数：

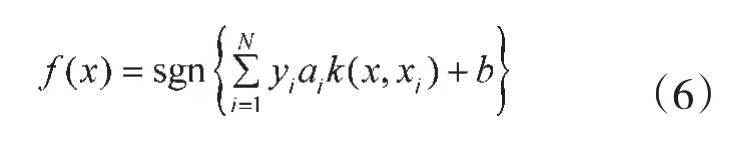
其中，K(xi,x)=Φ(xi)Φ(x)为核函数。采用不同的核函数可以实现多种从输入空间到特征空间的非线性映射形式，典型的核函数形式有以下3种。

多项式核函数：K(x,y)=[(x y)+1]d

径向基核函数：K(x,y)=exp{-γ‖x-y‖2}

Sigmoid核函数：K(x,y)=S[(xy)+c]

研究表明，在SVM 核函数的选取中，径向机核函数具有良好的非线性[11]，因此本文亦采用径向基核函数。

2.2 果蝇算法优化参数

FOA是台湾学者潘文超于2011 年提出的一种基于果蝇觅食行为推演出的寻求全局优化的方法[14]。果蝇嗅觉器官非常发达，可以很好地利用嗅觉和视觉上的优势搜集飘浮在空气中的各种气味并获食物源方向，然后飞近食物位置后亦可使用敏锐的视觉发现食物与同伴聚集的位置，并且向该方向飞去。

用果蝇优化算法系统来选择风机故障特征实现步骤如下。

步骤1：初始果蝇群体位置，随机设置果蝇群体的初始位置。

步骤2：赋予果蝇个体利用嗅觉搜寻食物的随机方向和距离(x0,y0)。

步骤3：估计果蝇与原点的距离（Dist），然后计算味道浓度的判定值(S)，此值为距离的倒数。

步骤4：将味道浓度判定值(S)带入味道浓度判定函数求出各果蝇个体位置的味道浓度（Smell）。

步骤5：找出此果蝇群体当中味道浓度最高的果蝇。

步骤6：找出此果蝇群体当中味道浓度最高的果蝇及其对应的果蝇群位置坐标，此时果蝇群内各个体果蝇利用视觉往该位置飞去。

步骤7：迭代寻优。重复执行步骤2～5，并判断味道浓度是否优于前一迭代味道浓度，若是则执行步骤(6)。

2.3 基于FOA的SVM参数优化

SVM 对非线性问题分类性能取决于相结合的几个因素，首先应该选择合适的径向基参数σ2将数据映射到高维的特征空间，然后对此特征空间寻找合适的惩罚因子C，使学习机的置信范围和经验风险具有最佳比例。因此对σ2和C 的联合优化具有重大的意义。为了便于编程，对SVM中核函数参数σ2做简单变换：1/σ2=g，把g作为径向基核函数参数进行研究，在此，使用FOA 算法对其进行优化，具体步骤如下：

1）初始果蝇群体的位置和参数的初始化。初始化果蝇群体位置区间为[1,2]，种群规模30，迭代次数为100，设定SVM的初始参数。

2）果蝇寻优开始。利用FOA调整参数C和g。

3）利用味道浓度判定函数求出味道浓度。

4）根据味道浓度值寻找极值，保留最佳位置。

5）检查结束条件。若满足,则结束寻优;否则转至(2)。结束条件为寻优达到最大进化代数或味道浓度是否优于前一个迭代味道浓度。

3 机组轴系振动及其故障特征提取

3.1 机组典型故障的振动

实验数据来自于东北电力大学流体机械实验室离心式风机实验台，试验采用的离心风机的型号为Y5-47-315D，主轴转速2 900r/min，风量1 890m3/h，风压8.09Pa，电机型号Y-90-Z，功率1.5kW，进口风温20℃，出口方向右0°。对风机动故障中较为常见的5种故障进行识别，故障类型为：转子不平衡，转子不对中，基座松动，动静摩擦，轴承内圈损坏。所采用故障信号通过风机故障试验台测取，数据采集选用INV306F 数据采集器，采样频率设为800Hz，采样时间为5s，数据存储及处理由与采集器连接的台式计算机完成。离心通风机试验的故障原始信号见图1。

图1 故障的振动信号图

为了提高信号频谱分析的幅值和相位精度，采用了多通道同步采集方式，并对采集的信号进行整周期截取。通过小波去噪后进行时域和频域分析，获得所有信号的时域特征参数和频域特征参数，并由此构成诊断所需的观测空间。其中，时域特征参数包括：波形指标、脉冲指标、峰值指标、裕度指标、歪度指标、峭度指标等6个无量纲参数；频域特征参数包括[15]：(0.01～0.49)X，0.5X，1X，2X，3X，(3～5)X，(5～10)X，odd X 等8 个频率或频段的频谱幅值或频谱幅值和。这里，X表示谐波，odd X 表示奇数倍谐波。这样，每个样本空间都由这14个特征参数构成。

每一样本都是一个14 维的向量，包含有14个特征属性。此时，用于识别的特征属性较多，为了简化判断识别过程，就要对多个识别特征属性所包含的信息进行浓缩，在保存样本整体信息的基础上，对特征属性的数量进行压缩。流形学习算法能够在保存样本的非线性信息的情况下对特征信息进行压缩，将振动故障样本矩阵作为流形学习算法的输入，选取d=6，以故障诊断精度为目标，选取最佳邻域值k=10，输出即为经过特征提取后的学习特征样本和测试特征样本。经过流形学习特征提取之后，每一特征样本由原来的14 个特征属性变成了由8 个特征属性组成的特征样本，其中这8个特征属性代表了每一样本的特征信息，并将每一样本的特征属性作为神经网络的输入征兆，用来诊断振动故障。首先每种算法都对每类故障各30 组特征向量共150 组样本进行训练。训练完成后，从训练样本以外的数据中每类故障随机抽取20组典型数据进行测试。

3.2 诊断结果及分析

SVM 分类器各核函数的参数均采用交叉验证的优化方法来确定，分别选用蚁群和粒子群两种智能算法与果蝇优化算法进行比较，本文分别采用ACO-SVM、PSO-SVM和FOA-SVM3种算法对上述样本进行识别，其中ACO-SVM，PSO-SVM，FOA-SVM 分别表示蚁群优化支持向量机，粒子群优化支持向量机和果蝇优化支持向量机。由于3 种算法都是全局寻优的概率搜索算法，因此参数均为如下设置：种群最大数量均为30，最大进化代数均为100，SVM参数C变化范围均为[10-1,10-2]，g 变化范围均为[10-2,10-3]。每种算法都对每类故障的30组训练集数据进行训练，用其余的20 组测试集数据进行测试。测试结果如下：

图2 测试结果图

图2中的accuracy为测试集识别的正确率，1为转子不平衡，2为转子不对中，3为基座松动，4为动静摩擦，5为轴承内圈损坏，对测试集的识别结果见表1。

表1 不同算法下的识别结果表

表1 可以看出，FOA-SVM 与PSO-SVM 在时间上相当，但在识别率上FOA-SVM 比PSO-LSSVM 高出6%。FOA-SVM 与ACO-SVM在识别率上分别达到99%和96%，都具有较高的识别率，但运行时间前者比后者快了接近一倍。所以经过FOA 算法优化过的SVM，无论在准确度上还是在运行时间上都优越于其余的两种算法，因此在风机振动故障类型识别上有很大的应用前景。

4 结论

1）在SVM参数优化方面。FOA算法比PSO算法更稳定，比ACO算法进化的更快。

2）在故障的识别率上。FOA 算法达到了99%，而PSO与ACO分别为93%和96%。

3）在运行时间上FOA 算法仅用了2.102s，PSO与ACO分别用了2.572s和3.406s。

相比之下，FOA-SVM 在参数优化上快速稳定，在识别率上最高、识别速度最快。

[1]李斌，柴岩.风机异常振动故障的诊断与治理[J].风机技术，2010（3）：80-82.

[2]李嵩，朱之墀.离心风机气动设计方法的发展及其应用[J].风机技术，2012（4）：60-67.

[3]李燕坡，刘广州，杨建.大型机组日常管理与维护[J].风机技术，2012（2）:86-88.

[4]张倩，张志新，王亮.基于振动测试的滚动轴承故障诊断技术进展[J].风机技术，2012（1）:60-70，78.

[5]刘宇，谭伟，闻婧.大型双馈风力发电机振动特性分析与故障诊断[J].风机技术，2012（4）:56-59.

[6]Burges C J C.A tutorial on support vectormachines for pattern recognition[J].DataMining and Knowledge Discovery，1998，2(2)：121-167.

[7]Wen-Tsao Pan.A new Fruit Fly Optimization Algorithm:Taking the financial distress model as an example [J].Knowledge-Based Systems,2012,26:69-74.

[8]赵丽基.基于粒子群算法神经网络的多重化整流电路智能故障诊断[D].中南大学，2008.

[9]Dorigo M，Maniezzo V，Colorni A.Ant system optimization by acolony of cooperating agents[J].IEEE Transactions on System,Man and Cybernetics-Part B：Cybernetics，1996，26(1)：29-41.

[10]陆静.蚁群算法在变压器故障诊断中的应用研究[D].南京航空航天大学，2008.

[11]S T Roweis,L K Saul.Nonlinear dimensionality reduction by locally linear embedding[J].Science,2000,290:2323-2326.

[12]J B Tenenbaum,V D Silva,J C Langford.A global geometric frame-work for nonlinear dimensionality reduction[J].Science,2000,290:2319-2323.

[13]陈高曙,曾庆宁.基于LLE 算法的人脸识别方法[J].计算机应用研究,2007,24(10)：176-178.

[14]潘文超.果蝇优化算法[M].台湾:沧海书局，2011.

[15]钟秉林,黄仁.机械故障诊断学[M].机械工业出版社，1997.