Matlab软件在高等数学教学课堂上的应用
2014-11-25龙松
龙 松
(华中科技大学武昌分校 基础科学部,湖北 武汉 430064)
Matlab软件在高等数学教学课堂上的应用
龙 松
(华中科技大学武昌分校 基础科学部,湖北 武汉 430064)
分别从不同方面举例阐述了Matlab软件在数学课堂教学中的若干应用。通过实例,一方面可以帮助学生更好地理解抽象的概念和复杂的理论知识,另一方面也让学生不再觉得数学枯燥,而是更加实用,生动有趣。
Matlab;高等数学;课堂教学
Matlab软件是目前最流行的科学计算语言,它的优越性体现以下几个方面:1)将数值计算功能、符号运算功能和图形处理功能高度地集成在一起,在数值计算、符号运算和图形处理上做到了无缝的衔接,极大地方便了用户;2)有大量事先定义好的的数学函数,并且有很强的用户自定义函数的能力,同时还提供了在多个应用领域解决难题的工具箱;3)具有与其它语言编写程序相结合的能力以及输入输出格式化数据的能力;4)具有基于HTML的完整的帮助功能;5)是一种“数学形式的语言”,有人称其为“演算纸”式科学算法语言。
如今,在我国的科研院所、大型公司或企业的工程计算部门,Matlab已是最为普遍的计算工具之一。许多高校,特别是重点高校,Matlab课程的开设已不再仅仅局限于选修课,而开始逐渐成为公共基础课。若能在大学数学课堂教学中利用Matlab的优势,势必会产生良好的效果。本文结合教学经历,举例具体说明Matlab在数学教学中的应用,希望能够起到抛砖引玉的效果。
例1 定积分概念的诠释
在绝大数高等数学课本上,都会以求曲边梯形的面积来引入定积分的概念,在求解过程中,大致都是以下4个步骤:1)分割;2)近似;3)求和;4)求极限。在教学过程中,教师大都只能用语言去进行描述,而学生不能从直观上来感觉整个计算过程。为了加强对整个概念的理解,如果能够用计算机进行近似模拟,并辅以直观的图像,则会起到事半功倍的效果。
如计算曲线y=sinx在区间[0,π]上与x轴所围成的图形的面积,此时我们可采用复合梯形积分法的思路编写以下主调用程序Trapezd.m:
程序名称 Trapezd.m[1]
调用格式 I=Trapezd('f_name',a,b,n)
程序功能 用复化梯形公式求定积分值
输入变量 f_name为用户自己编写给定函数y=f(x)的M函数而命名的程序文件名;a为积分下限,b为积分上限,n为积分区间[a,b]划分成小区间的等份数
输出变量 I为定积分值
程 序 function I=Trapezd(f_name,a,b,n)
h=(b-a)/n;x=a+(0:n)*h;f=feval(f_name,x); I=h*(sum(f)-(f(1)+f(length(f)))/2);
hc=(b-a)/100;xc=a+(0:100)*hc;fc=feval(f_name,xc);plot(xc,fc,'r'); hold on;
title('Trapezoidal Rule');xlabel('x');ylabel('y');plot(x,f);plot(x,zeros(size(x)));
for i=1:n;
plot([x(i),x(i)],[0,f(i)]);
end
将以function开头和以end结束的程序在Matlab中保存为以Trapezd命名的函数,并保存在Matlab程序搜索路径之下,然后我们就可以调用该函数来近似求解曲边梯形的面积,进而去诠释定积分的概念。
我们先编制y=sinx的M函数,程序文件命名为sin_x.m。
function y=sin_x(x) y=sin(x);
如果我们将区间分隔4等份,调用格式为figure(1), I=Trapezd('sin_x',0,pi,4)
计算结果为:I=1.8961,见图1
如果我们将区间分隔40等份,调用格式为:figure(2),I=Trapezd('sin_x',0,pi,40)
计算结果为:I= 1.9990,见图2
如果我们将区间分隔100等份,调用格式为:figure(3),I=Trapezd('sin_x',0,pi,100)
计算结果为:I= 1.9998,见图3
如果我们将区间分隔200等份,调用格式为:figure(4),I=Trapezd('sin_x',0,pi,200)
图1、2、3和图4分别表示了分割、近似、求和的过程,同时可以看出划分越细,计算结果就越接近真实值2。从中很清楚地知道定积分的几何意义:对于分割越精细,计算结果也就越接近真实值的道理,这样就更能理解定积分是和式求极限的计算了。

图1 4等分复化梯形图

图2 40等分复化梯形图

图3 100等分复化梯形图

图4 200等分复化梯形图
例2 图形展示[2]
在定积分的应用中,常常会要求计算图形的面积,要求大致绘出图形以确定积分上下限。可是有些图形,特别是极坐标下的平面图形和空间中的立体图形,往往难以绘制。若能利用Matlab的绘图功能,绘制出较精确的图形,给学生以直观的感觉,教学效果就会更加的理想。例如求由曲线r=3cosθ,r=1+cosθ所围成图形的公共部分的面积。
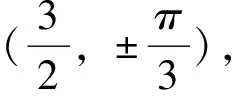
t=0:0.1:2*pi;r1=3*cos(t);r2=1+cos(t);polar(t,r1);hold on;polar(t,r2)
得到如图5所示,根据图5,我们很快得出面积算式为:

图5 极坐标下两曲线相交图

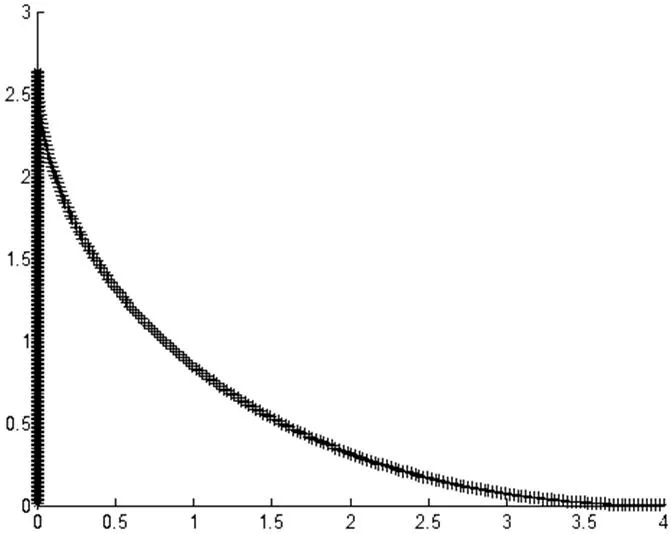
图6 重要极限Ⅰ函数曲线图
在例2中,通过图形的绘制,可以清楚的看出所围成的图形关于横坐标对称,这样所求的面积等于横坐标上方图形的面积的2倍,从而可以减少计算量;另外可以清楚的看出两曲线的相交的位置,从而为积分的上下限的选择带来了极大的方便,从而保证了积分算式的准确性。
x=-10:0.1:10;x=x+eps;y=sin(x)./x;plot(x,y,[0],[1],'or')
例3 方程组求解
Matlab是矩阵实验室Matrix Laboratory的简写,最早也是为了矩阵的计算而应运而生的,如果在教学中,采用Matlab进行计算,将会大大节省繁琐的计算时间,而把更多的精力投入到概念和定理的理解上去。Matlab提供了很多关于矩阵的计算函数,例如逆矩阵函数inv(),方阵的行列式函数det(),方阵的行初等变换函数rref(),方阵的特征值、特征向量函数eig()等等。利用已有的函数,我们可以实现对线性方程组的解的各种情况的判定,这样可以使我们对于线性方程解的定理有更深的理解。可编写出以下程序,在提示下输入系数矩阵A和常数列b,然后程序语言自动给出线性方程组AX=b在各种情况下的求解答案,并同时显示其增广矩阵(A⋮b)的行最简形。
程序如下:
A=input('Please input matrix A:');b=input('Please input matrix b:');
B=[A,b];zuijianxing=rref(B),n=size(A);R_A=rank(A);R_B=rank(B);
format rat
if R_A==R_B&R_A==n(2)
X=A/b
elseif R_A==R_B&R_A X=pinv(A)*b ,C=null(A,'r') else X='equition no solve' end 将以上程序保存名为mm1.m,并放在搜索路径之下,然后在命令窗口输入:mm1,按照屏幕提示分别输入系数矩阵A和常数列b。 情形1: Please input matrix A:[1 2;3 4] % [1 2;3 4]为键盘输入的 Please input matrix b:[1;2] % [1;2]为键盘输入的 zuijianxing = % 从行最简形可知,方程有唯一解 1.0000 0 0 0 1.0000 0.5000 X = % 唯一解 0 1/2 情形2: Please input matrix A:[1 2;2 4] Please input matrix b:[1;3] zuijianxing = 1 2 0 0 0 1 X = equition no solve 可见方程组无解,这从行最简形也能看出:R(A)≠R(A⋮b) 情形3: Please input matrix A:[1 2;2 4] Please input matrix b:[1;2] zuijianxing = % 从行最简形可知,方程组有无穷多解 1 2 1 0 0 0 X = % 方程组的特解 1/5 2/5 C = % 对应齐次方程组解空间的基础解系 -2 1 通过该程序,大大压缩了计算过程和时间,使其非常清晰地看到不同情况下方程组的解的情况,从而能更好地理解方程组的解的判断定理。 例4 动态仿真[3] 当建立方程模型很困难时,我们可以用计算机仿真法对系统进行分析研究,即利用计算机对实际动态系统的结构和行为进行编程、模拟和计算,以此来预测系统的行为效果。例:海上边防缉私艇发现距c公里处有一走私船正以匀速a沿直线行驶,缉私艇立即以最大速度b追赶,在雷达的引导下,缉私艇的方向始终指向走私船。问缉私艇经历多长时间追赶上走私船?并求出缉私艇追赶的路线。 我们设定走私船初始位在点(0,0),方向为y轴正方向,缉私艇的初始位在点(c,0)。我们事先给定一个距离,比如d=0.005 km,如果算出的两船的距离小于0.005 km,则认为缉私艇已经追上了走私船,否则让时间产生一个步长,返回到上一步继续进入下一次循环;当从循环退出以后,我们根据记录的两船坐标,即可绘出轨迹图。我们事先假定c=4km,a=0.4/60(km/s),b=0.8/60(km/s) 主程序如下: c=4; a=0.4/60; b=0.8/60;d=0.005;dt=2;t=0; jstx=c;jsty=0;zscx=0;zscy=0;hold on;axis([0,4,0,3]) while (sqrt((jstx-zscx)^2+(jsty-zscy)^2)>d) t=t+dt; jstx=jstx-b*dt*jstx/sqrt(jstx^2+(a*t-jsty)^2); jsty=jsty+b*dt*(a*t-jsty)/sqrt(jstx^2+(a*t-jsty)^2); zscy=a*t; plot(jstx,jsty,'r+',zscx,zscy,'b*') pause(0.01) end jstx,jsty,zscx,zscy,t 将以上程序保存名为mm2.m,并放在搜索路径之下。然后在命令窗口输入:mm2,可得:jstx = 2.8712e-005,jsty = 2.6382,zscx =0,zscy = 2.6400,t = 396。 即历时:396 s,最后艇的坐标为:(0.000 028 712,2.638 2),船的坐标为:(0,2.640 0)。 图7 缉私艇追击路线图 图7显示了追击的路线图,通过图7展示,能很清楚的了解整个追赶过程,对动态仿真有了直观的感受,同时也极大的鼓舞了对实际问题的分析的兴趣,并拓宽了学习的思维方式。 在数学课堂教学中,如果将Matlab软件应用于其中,一方面可以帮助学生更好地理解抽象的概念和复杂的理论知识,增加直观的印象,以期达到事半功倍的效果,激发其学习的兴趣;另一方面也能摆脱其繁琐的计算,让学生能把更多的精力投入到概念的理解上和模型的建立上,以期达到其提高实践动手能力,培养其学数学、用数学的理念,同时也让数学学习不再枯燥,而是更加实用,生动有趣。 [1] 李林,金先级.数值计算方法[M].北京:高等教育出版社,2006.2:76-77. [2] 李海涛,邓樱.MATLAB程序设计教程[M].北京:高等教育出版社,2002.8:94-105. [3] 李继成.数学实验[M].西安:西安交通大学出版社,2003.8:150-157. (王菊平) G642.0 A 1003-8078(2014)03-0074-05 2014-04-23 doi 10.3969/j.issn.1003-8078.2014.03.18 龙松,男,湖北武汉人,讲师,硕士,研究方向为金融工程、概率统计。