三电平SVPWM 与CBPWM 算法的内在联系研究
2014-11-25宋文胜冯晓云葛兴来丁荣军
方 辉 宋文胜 冯晓云 葛兴来 丁荣军,2
(1.西南交通大学电气工程学院 成都 610031 2.南车株洲电力机车研究所有限公司 株洲 412001)
1 引言
脉宽调制(Pulse Width Modulation,PWM)技术是交流调速系统的关键环节,其设计的好坏直接关系到整个系统的性能。在高速列车牵引传动系统的变频调速系统中,牵引变流器的控制一般采用PWM 技术,常用的调制策略有载波脉宽调制(Carrier-Base PWM,CBPWM)和空间矢量脉宽调制(Space Vector Pulse Width Modulation,SVPWM)两种[1-6]。SVPWM 从电机的角度出发,着眼于让电机获得幅值不变的圆形磁场,其直流电压利用率高,逆变器输出波形的谐波性能好。CBPWM 则从电源出发,目的是生成一个既可以调压又可以调频的三相正弦电源,其直接通过调制波与载波比较的方法实现,运算量较小,易于实现。虽然 SVPWM和CBPWM 的出发点不同,但是两者都是基于一个采样周期内的电压积分等效规则,因此它们的控制本质是相同的。
SVPWM 与CBPWM 的内在联系不仅能为两者的相互转换提供基础,并且能够为产生新的更优的调制器提供一定的条件。因此,国内外很多学者对两者的内在联系展开了研究[7-12]。文献[7,8]推导出了CBPWM 的基波调制函数与SVPWM 的空间矢量之间的关系,文献[9,10]较全面分析了两者在线性范围内的关系,文献[11]则利用此关系提出一种新的简单的SVPWM 算法。文献[12]推导出了过调制范围内两者之间的联系,得出SVPWM 在全调制度内都是一种特殊的CBPWM 的结论。虽然这些文献在研究SVPWM 与CBPWM 之间的关系方面已经取得了很多成果,但是都是基于两电平逆变器,并未涉及三电平。三电平中点钳位(Neutral Point Clamped,NPC)逆变器相对于两电平逆变器具有单管承受电压低,输出电压波形好,等效开关频率高等优点[13-15]。所以其一直是当今电力电子与电力传动领域的研究热点[16-19]。关于三电平SVPWM 与CBPWM的内在联系,文献[20-23]均从零矢量的角度分析了两者的联系,本文则从调制函数的角度出发,旨在找出与SVPWM 等效的CBPWM 的两路调制函数关于调制度的具体表达式,根据此表达式总结出调制函数的变化趋势,为进一步设计出更优的调制器提供一定的参考。
本文首先介绍了三电平逆变器的常规SVPWM算法,然后根据CBPWM 规则采样原理分析了双载波调制的特点,并根据此特点推导出与三电平逆变器SVPWM 算法等效的CBPWM 调制函数形式,最后通过仿真和实验验证了两者的等效性。
2 三电平逆变器SVPWM 算法
2.1 三电平NPC 逆变器电路拓扑与SVPWM 矢量分布
三电平NPC 逆变器的电路拓扑如图1 所示,逆变器每相桥臂均有四个全控开关器件,4 个续流二极管,2 个钳位二极管。由于钳位二极管的作用,每相输出p、o、n 三种电平,定义开关函数为

式中,x代表a、b、c 三相。

图1 三电平NPC 逆变器电路拓扑Fig.1 Topology of three-level NPC inverter
显然,SA,SB,SC共有33=27 种组合。空间电压矢量U定义为
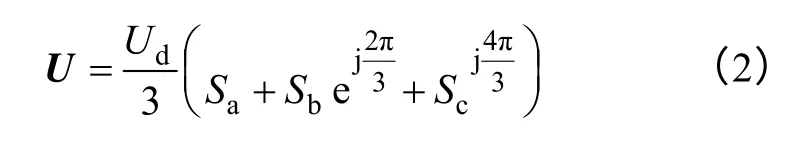
将每种开关状态代入式(2),可以得到电压矢量可分为3 个零矢量,12 个幅值为Ud/3 的小矢量,6 个幅值为的中矢量,以及6 个幅值为2Ud/3的大矢量,如图2 所示。

图2 三电平NPC 逆变器空间电压矢量图Fig.2 Space vector diagram of three-level NPC inverter
当参考电压矢量Uref位于第一扇区的I 区时,如图2 所示,根据相邻三矢量选取原则,其可用U0、U1、U5进行合成,各矢量的作用时间可根据伏秒平衡原理计算出来,即
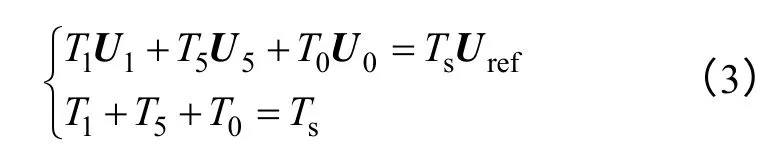
式中,T0、T1、T5分别为矢量U0、U1、U5的作用时间;Uref为目标参考电压矢量;Ts为开关周期。
2.2 开关序列
在同样采取相邻三矢量进行参考电压合成的情况下,3 个基本矢量的作用顺序,冗余矢量的选择,以及首发矢量的选择均会对输出电压的谐波含量以及开关损耗产生一定的影响。常规的三电平逆变器连续调制时,将矢量的合成分为7 个时间段,考虑避免窄脉冲以及减少开关损耗,第一扇区的第Ⅰ、Ⅱ区的矢量作用顺序如图3 所示。其中k是分配因子。其他区域的开关顺序类似。
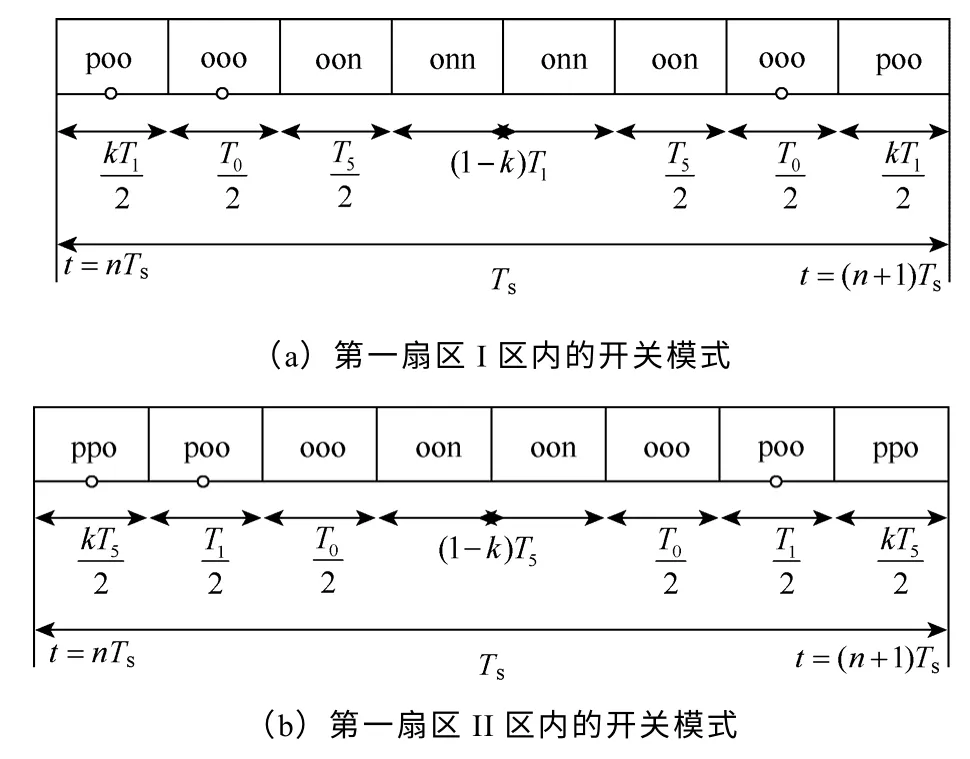
图3 第一扇区的开关模式Fig.3 The switch modes in sector 1
3 双载波PWM 工作特点
CBPWM 通过调制波与载波直接比较来产生PWM 波,其运算量小,易于实现,有利于高速实时运行。为了实现三电平逆变器的调制,需要有2个三角载波,如图4 所示,其中称幅值大于0 的三角载波为正三角载波,否则为负三角载波。图4 同时显示了调制波与两个三角载波大小关系的三种情况。

图4 双载波PWMFig.4 Double carrier signal PWM
在情况①中,调制波的幅值同时大于两三角载波的幅值,此时根据图中的几何关系,存在比例关系

式中,δ1为正脉宽时间;u1(t)为调制函数表达式;td为采样时刻;Um为三角载波的幅值。
设三角载波的幅值Um=1,则根据式(4)得到规则采样下情况①中的调制函数为

情况②中,调制波的幅值处于两个三角载波幅值之间,此时有

情况③时的调制函数可表示为

4 与SVPWM 等效的CBPWM 调制函数
在采用双载波PWM 时,当a 相调制函数处于情况①时,对应图1 中的三电平NPC 逆变器的开关函数Sa=1,也就是VTa1和VTa2导通;当a 相调制函数处于情况③时,对应的开关函数Sa=-1,也就是VTa3和VTa4导通;其他情况下为VTa2和VTa3导通。由此可以推出以下两个结论:
(1)开关VTa1和VTa3的开通与关断状态总是相反,开关VTa2与VTa4相反。
(2)开关VTa1的工作状态只取决于调制函数与正三角载波幅值的大小关系,与负三角载波无关;而 VTa4的工作状态只取决于调制函数与负三角载波幅值的大小关系,与正三角载波无关。
基于前面两点结论,为了方便推导出与SVPWM 等效的CBPWM 调制函数,本文将采用两路独立的调制波,一路正调制波用于和正三角载波比较从而产生VTa1与VTa3的开关控制信号,另外一路负调制波则用于和负三角载波比较来产生VTa2和VTa4的开关控制信号。
首先定义调制度m为

根据图2 的特点,可将整个线性调制区域分为三段。第一段为目标参考电压矢量的幅值小于或等于内六边形的内切圆(图2 中粗实线所示)半径值,根据调制度的定义,此时的调制度。在第一扇区内,第一段内的目标电压矢量的运动轨迹只在小三角形Ⅰ、Ⅱ内。第二段为目标参考电压矢量的幅值位于内六边形的内切圆半径值和外接圆半径值之间,同样根据调制度的定义,此时的调制度m处于范围内。在第一扇区内,第二段的目标参考电压矢量的运动轨迹依次经过小三角形Ⅰ、Ⅳ、Ⅴ、Ⅱ内。第三段的目标参考电压矢量的幅值位于内六边形的外接圆半径值和外六边形的内切圆半径值之间,调制度满足,此时的目标参考电压矢量在第一扇区的运动轨迹将依次经过小三角形Ⅲ、Ⅳ、Ⅴ、Ⅵ。
当调制度很小,处于第一调制段时,根据图3的开关模式,各扇区内a 相的正脉宽时间见表1,其中k为零矢量分配因子。

表1 各开关组合的作用时间Tab.1 Operating time of switch combination s
将以式(3)计算出来的矢量作用时间代入表1,并结合式(5)可以得到一个调制周期内正调制函数的表达式为

同理根据Sa=-1 的作用时间,结合式(7)可得到负调制波表达式为

在常规七段式算法中,零矢量分配因子k=0.5,代入式(9)、式(10)比较可看出负调制波可由正调制波平移π 后将幅值取相反数后得到,即

同时由式(9)、式(10)可以看出,不管k取何值,正负调制波均有半个周期函数值为0,且正调制波等于0 时,负调制波不为0,正调制波不等于0 时,负调制波为0。因此在不违背电压等效原则的情况下,即调制波调制产生的电压应不变的原则,可以将正负调制波相加得到一路调制波,并以此与两路三角载波进行比较产生开关控制信号。
当调制度处于第二调制段时,目标参考电压矢量的运动轨迹依次经过小三角形Ⅰ、Ⅳ、Ⅴ、Ⅱ内,此时第一扇区的正脉宽时间将经历四次变化,如图5 所示,则推导出的调制函数也分为4 段。

图5 第一扇区的目标参考电压矢量Fig.5 The desired reference voltage vector in sector 1
在△OMN中,根据正弦定理有

则解出参考电压矢量的相位角φ为

推导第二调制段内与SVPWM 等效的CBPWM调制函数的过程与第一段类似,第一扇区内正调制波的表达式为

当分配因子k=0.5 时,负调制波可由式(11)、式(14)得到。其他扇区以此类推。
当调制度处于第三调制段时,与第二调制段不同的是目标参考电压矢量在第一扇区内的运动轨迹依次经过区域Ⅲ、Ⅳ、Ⅴ、Ⅵ,因此其Sa=1 的作用时间也不一样,但是此时推导与 SVPWM 等效的CBPWM 调制函数表达式过程与第二调制段类似。正调制函数在第一扇区内表达式为
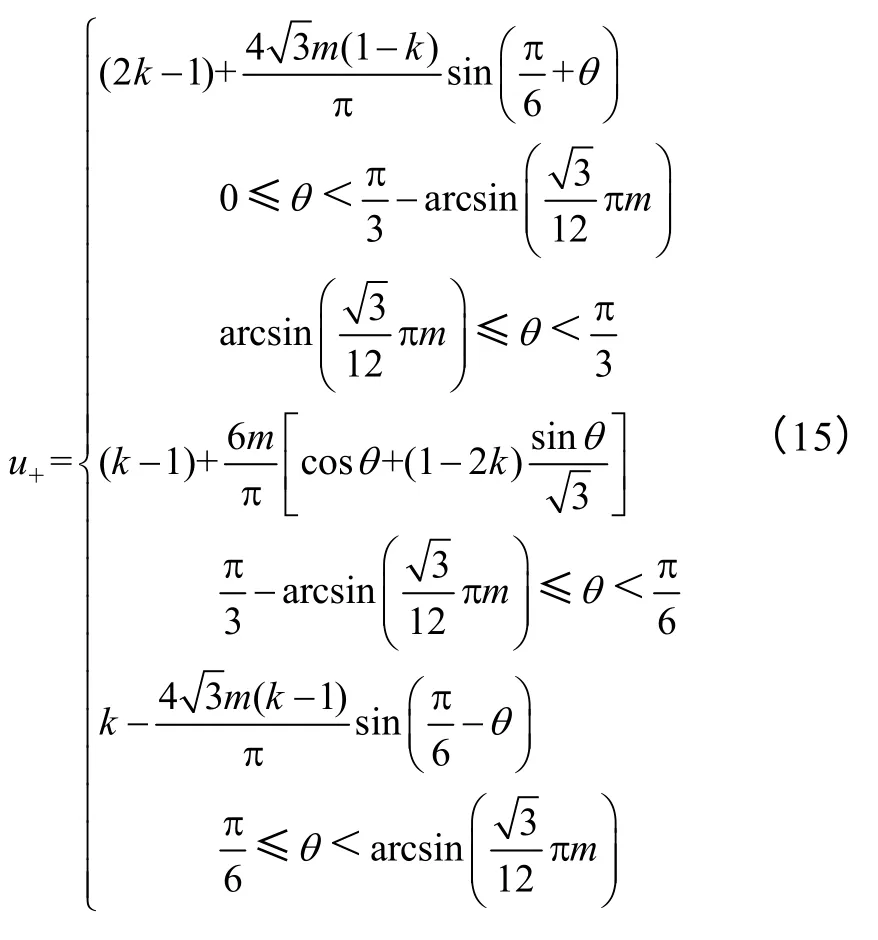
当分配因子k=0.5 时,负调制波可由式(11)、式(15)得到。其他扇区以此类推。
5 仿真研究
为了验证以式(9)、式(10)、式(14)、式(15)为调制函数的CBPWM 分别与SVPWM 第一调制段、第二调制段和第三调制段等效,在 Matlab/Simulink 环境下搭建了SVPWM和CBPWM 算法的模型。模型中直流侧电压取3kV,开关频率1 050Hz,第一调制段内调制度m取0.1,第二调制段内调制度取0.5,第三调制段内调制度取0.8,两者输出的相电压谐波频谱图分别如图6、图7和图8 所示。从频谱图可以看出,两者输出的相电压不仅总谐波畸变率(Total Harmonic Distortion,THD)值近似相等,谐波分布情况也基本一样。同时可以看出高次谐波主要集中在2 倍开关频率附近。
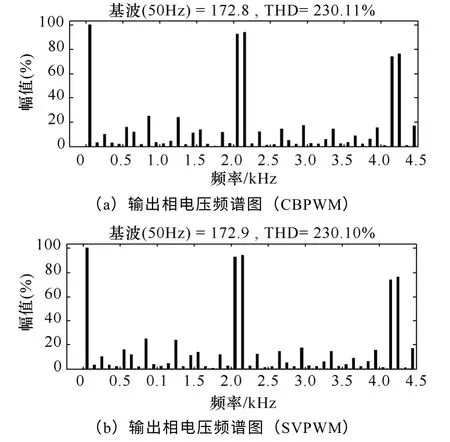
图6 m=0.1 时两者输出的相电压频谱图Fig.6 The FFT of output voltage spectra when m=0.1

图7 m=0.5 时两者输出的相电压频谱图Fig.7 The FFT of output voltage spectra when m=0.5

图8 m=0.8 时两者输出的相电压频谱图Fig.8 The FFT of output voltage spectra when m=0.8
由前面的推导可知,在整个线性调制范围内,与SVPWM 等效的CBPWM 调制函数是关于调制度m和分配因子k的函数,常规的SVPWM 中k=0.5。图9 反映了随着调制度增大调制函数的变化趋势。
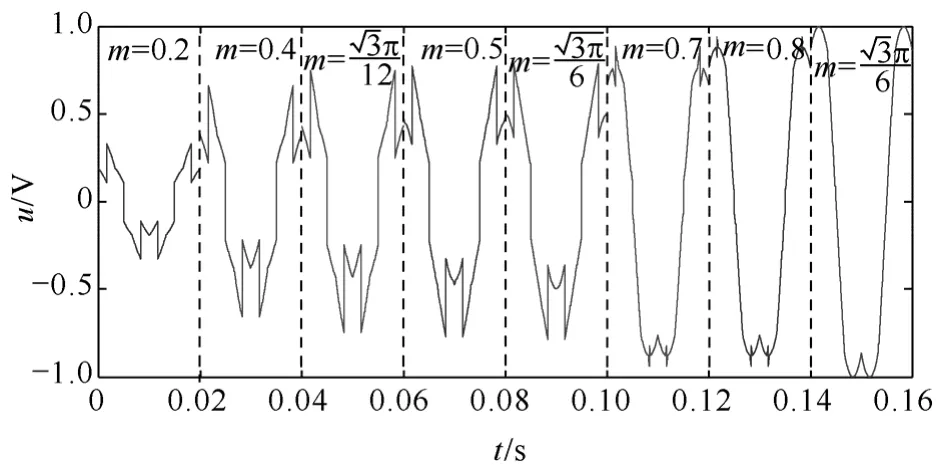
图9 不同调制度下CBPWM 的调制函数Fig.9 Modulating functions of CBPWM with different modulation index m
由图9 可知,当调制度处于第一调制段时,调制函数在π/3 的电角度内改变了一次,这与前面理论分析中目标参考电压矢量运动轨迹经过小三角形I和II 相符。当调制度继续增大,达到调制第二段时,目标参考电压矢量轨迹分为3 段,于是调制函数在π/3 的电角度内改变了两次。当达到线性调制的上限时,与其等效的CBPWM 调制波刚好为鞍形波,此时与两电平SVPWM 完全一样,这是因为目标参考电压矢量的运动轨迹只经过小三角形Ⅲ、Ⅵ,三角形Ⅳ、Ⅴ只处于临界状态。
6 实验研究
为了进一步验证SVPWM 与CBPWM 的等效性,本文基于TMS320F2812 编写出了两者的算法,并进行了半实物测试实验。实验中,直流电压为3kV,开关频率为1 050Hz。由于逆变器调制度比较小时,Uref仅由小矢量和零矢量合成,逆变器不再工作在三电平输出模式,限于篇幅实验部分未考虑这种情况。图10、图11 分别为调制度取0.5和0.8时两者输出的相电压及其谐波分析图,表2 给出了两者输出相电压在两倍开关频率附近的主要谐波含量,经过对比可知,两者的谐波分布及主要谐波含量都相等,充分验证了等效关系。

图10 m=0.5 时两者输出相电压及其频谱图Fig.10 The FFT of output voltage spectra when m=0.5


图11 m=0.8 时两者输出相电压及其频谱图Fig.11 The FFT of output voltage spectra when m=0.8
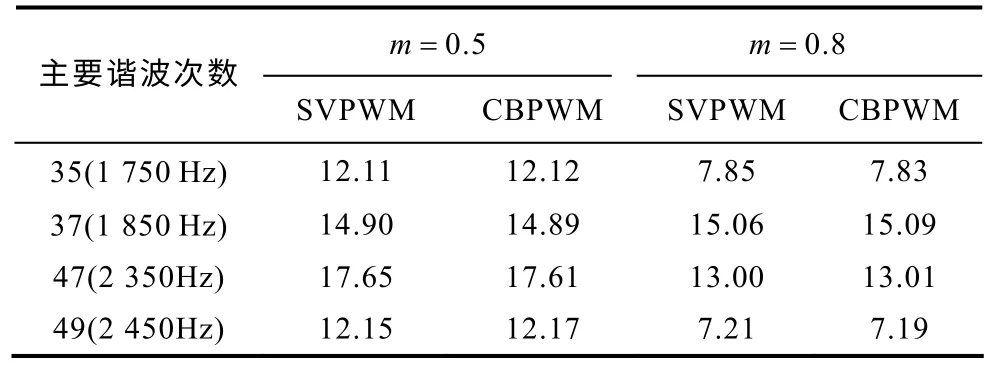
表2 m=0.5和m=0.8 时两者输出相电压主要谐波含量Tab.2 The main harmonic content of output line voltage when m=0.5 and m=0.8(%)
7 结论
为了揭示三电平NPC 逆变器SVPWM 算法与CBPWM 的内在联系,本文首先分析了三电平SVPWM 算法的原理以及双载波PWM 的工作特点,然后从调制函数角度找出了与 SVPWM 等效的CBPWM 调制函数关于调制度的具体表达式,并总结出随着调制度变化调制函数的变化规律。最后,得出三电平SVPWM 也是一种特殊形式的CBPWM算法的结论。对两者关系的深入分析与理解,有利于设计出性能更优的调制器。最后仿真和实验结果验证了理论分析的正确性。
[1]文小玲,尹相根,张哲.三相逆变器统一空间矢量PWM 实现方法[J].电工技术学报,2009,24(10):87-93.Wen Xiaoling,Yin Xianggen,Zhang Zhe.Unified space vector PWM implementation method for three phase inverters[J].Transactions of China Electrotechnical Society,2009,24(10):87-93.
[2]Pou J,Zaragoza J,Ceballos S,et al.A carrier-based pwm strategy with zero-sequence voltage injection for a three-level neutral point clamped converter[J].IEEE Transactions on Power Electronics,2012,27(2):642-651.
[3]Reddy B V,Somasekhar V T,Kalya Y.Decoupled space-vector pwm strategies for a four-level asymmetrical open-end winding induction motor drive with waveform symmetries[J].IEEE Transactions on Industry Electronics,2011,58(11):5130-5141.
[4]周卫平,吴正国,唐劲松,等.SVPWM 的等效算法及SVPWM 与SPWM 的本质联系[J].中国电机工程学报,2006,26(2):133-137.Zhou Weiping,Wu Zhengguo,Tang Jinsong,et al.A novel algorithm of SVPWM and the study on the essential relationship between SVPWM and SPWM[J].Proceedings of the CSEE,2006,26(2):133-137.
[5]Nguyen T D,Lee H H.Modulation strategies to reduce common-mode voltage for indirect matrix converters[J].IEEE Transactions on Industry Applications,2012,59(1):129-140.
[6]Jones M,Dujic D,Levi E,et al.Switching ripple characteristics of space vector PWM schemes for five-phase two-level voltage source inverters—part 2:current ripple[J].IEEE Transactions on Industry Electronics,2011,58(7):2799-2808.
[7]Bowes S R,Lai Y S.The relationship between space-vector modulation and regular-sampled PWM[J].IEEE Transactions on Industry Electronics,1997,44(5):670-679.
[8]Blasko V.Analysis of a hybrid PWM based on modified space-vector and triangle comparison method[J].IEEE Transactions on Industry Applications,1997,33(3):756-764.
[9]Iqbal A,Moinuddin S.Comprehensive relationship between carrier-based PWM and space vector PWM in a five-phase VSI[J].IEEE Transactions on Power Electronics,2009,24(10):2379-2390.
[10]Zhou K L,Wang D W.Relationship between spacevector modulation and three-phase carrier-based PWM a comprehensive analysis three-phase inverters[J].IEEE Transactions on Industry Applications,2002,49(1):186-196.
[11]陆海峰,瞿文龙,张磊,等.基于调制函数的SVPWM 算法[J].电工技术学报,2008,23(2):37-43.Lu Haifeng,Qu Wenlong,Zhang Lei,et al.SVPWM algorithm based on modulation functions[J].Transactions of China Electrotechnical Society,2008,23(2):37-43.
[12]方辉,冯晓云,葛兴来,等.过调制区内两电平SVPWM 与CBPWM 算法的内在联系研究[J].中国电机工程学报,2012,32(18):23-30.Fang Hui,Feng Xiaoyun,Ge Xinglai,et al.Relationship studies between two-level SVPWM and CBPWM in the over-modulation region[J].Proceedings of the CSEE,2012,32(18):23-30.
[13]Teichmann R,Bernet S.A comparison of three level converters versus two-level converters for lowvoltage drives,traction and utility applications[J].IEEE Transactions on Industry Applications,2005,41(3):855-865.
[14]胡存刚,王群京,李国丽,等.基于虚拟空间矢量的三电平 NPC 逆变器中点电压平衡方法[J].电工技术学报,2009,24(5):100-107.Hu Cungang,Wang Qunjing,Li Guoli,et al.A neutralpoint potential balancing algorithm for three-level inverter based on virtual-space-vector[J].Transactions of China Electrotechnical Society,2009,24(5):100-107.
[15]张瑾,齐铂金,张少如.Z 源三电平中点钳位逆变器的空间矢量调制方法[J].电工技术学报,2010,25(9):108-114.Zhang Jin,Qi Bojin,Zhang Shaoru.A space vector PWM algorithm for Z-source three-level NPC inverters[J].Transactions of China Electrotechnical Society,2010,25(9):108-114.
[16]胡海兵,姚文熙,吕征宇.三电平空间矢量调制的FPGA 实现[J].电工技术学报,2010,25(5):116-128.Hu Haibing,Yao Wenxi,Lü Zhengyu.Realization of three level SVPWM using FPGA[J].Transactions of China Electrotechnical Society,2010,25(5):116-128.
[17]金舜,钟彦儒,明正峰,等.一种控制中点电位并消除窄脉冲的三电平PWM 方法[J].中国电机工程学报,2003,23(10):114-118.Jin Shun,Zhong Yanru,Ming Zhengfeng,et al.A three-level PWM method of neutral-point balancing and narroe-pulse elimination[J].Proceedings of the CSEE,2003,23(10):114-118.
[18]姜卫东,王群京,陈权,等.一种完全基于两电平空间矢量调制的三电平空间矢量调制算法[J].电工技术学报,2009,24(1):108-114.Jiang Weidong,Wang Qunjing,Chen Quan,et al.SVPWM strategy for three-level inverter based on SVPWM strategy for two-level inverter[J].Transactions of China Electrotechnical Society,2009,24(1):108-114.
[19]Pou J,Boroyevich D,Pindado R.New feed forward space-vector PWM method to obtain balanced AC output voltages in a three-level neutral-point-clamped converter[J].IEEE Transactions on Industry Electronics,2002,49(5):1026-1034.
[20]吴洪洋,何湘宁.多电平载波PWM 法与SVPWM法之间的本质联系及其应用[J].中国电机工程学报,2002,22(5):11-15.Wu Hongyiang,He Xiangning.Relationship between multilevel carrier-based PWM and SVPWM and its applications[J].Proceedings of the CSEE,2002,22(5):11-15.
[21]宋文祥,艾芊,云伟俊,等.基于矢量分区的三电平 SVPWM 模式零序分量分析[J].电工技术学报,2009,24(12):102-108.Song Wenxiang,Ai Qian,Yun Weijun,et al.Zerosequence signal of space vector modulation for three level neutral-point-clamped inverter based on vector diagram partition[J].Transactions of China Electrotechnical Society,2009,24(12):102-108.
[22]陈娟,何英杰,王新宇,等.三电平空间矢量与载波调制策略统一理论研究[J].中国电机工程学报,2013,33(9):71-78.Chen Juan,He Yingjie,Wang Xinyu,et al.Research of the unity theory between three-level space vector and carrier-based PWM modulation strategy[J].Proceedings of the CSEE,2013,33(9):71-78.
[23]Yao W X.Comparisons of space-vector modulation and carrier-based modulation of multilevel inverte[J].IEEE Transactions on Power Electronics,2008,23(1):45-51.
