动态电压恢复器的谐波补偿数字控制技术

王建伟 胡晓光 陈松松

（北京航空航天大学自动化科学与电气工程学院 北京 100191）

1 引言

动态电压恢复器（Dynamic Voltage Restorer，DVR）是一种新型的动态电能质量串联补偿装置，能够实时检测系统电压，当发生电压跌落时，其逆变单元能够瞬时产生动态补偿电压，在ms 级时间内将跌落电压补偿至额定值，保证了系统敏感负载的正常运行[1-3]。

为了实现快速和精确的电压补偿，国内外相关研究人员对DVR 的控制策略做了大量的研究工作。前馈控制是出现最早、并被广泛应用于实际装置的一种方法，但是由于其为开环控制，无法实现对周期性正弦信号的无静差跟踪，容易出现过补偿或欠补偿的现象，难以实现对电压跌落的精确补偿[4]。文献[5]提出了基于电容电流内环、补偿电压外环反馈以及系统电压前馈的复合控制策略，增大了控制系统的稳定裕度，并提高了其动态响应速度。但是，忽略了三相电压不平衡跌落以及电容电流瞬时值检测困难等问题。文献[6]采用的重复控制方法理论上可以在稳态条件下实现对给定信号的完美跟踪，提高系统的稳态精度，但是控制器结构复杂，并且控制器固有的延时特性也使其不适用于动态响应速度要求较高的DVR 应用场合。除此之外的诸多控制策略[7-10]也都解决了DVR 控制过程中存在的一些问题和难点，但是很少有DVR 控制策略考虑到逆变单元开关器件的死区时间、非线性负载等因素产生的低次谐波电流会造成电压波形畸变[11]，以及数字控制带来的计算延时等对DVR 动态特性的不利影响。

为了提高DVR 逆变单元抑制低次谐波的能力，克服数字控制对系统性能的影响，保证DVR 能有更高质量的电压补偿效果。本文提出一种基波比例谐振（Proportional Resonant，PR）控制电压外环和指定次谐波PR 控制电感电流内环的双闭环数字控制策略。PR 控制器在谐振频率处的开环增益无穷大，理论上可以实现对特定频率给定信号的无静差控制，同时在其他频率处可以提供足够的衰减防止相邻频率间的干扰[12]。由于电压外环带宽较窄，不能在外环采用谐波PR 控制，因此只能通过在电压外环采用基波PR 控制、在电感电流反馈内环采用谐波PR 控制来消除稳态误差和补偿指定次谐波。采用的数字控制方法，避免了采样、计算延时等对稳态误差和动态响应特性的影响。在理论研究的基础上开发了11kV·A 的DVR 样机，并进行了相应的测试，理论研究和测试结果表明了提出的控制策略的有效性和可行性。

2 逆变单元拓扑结构及其数学模型

目前，在DVR 逆变单元中使用较多的拓扑结构是三单相H 桥结构，三相之间没有相互耦合，电路相对独立，控制也相对简单[13,14]。因此，本文DVR样机逆变单元的拓扑结构也采用三单相H 桥结构。由于三单相H 桥逆变单元结构、控制方法相同，因此仅以图1 所示的单相H 桥逆变单元为例进行讨论。其中Ed为直流母线电压，ui为逆变单元输出电压，uo为补偿电压，iL为滤波电感电流，iC为滤波电容电流，io为负载电流，考虑滤波电感L的等效电阻、开关与通态损耗、死区效应等逆变单元的各种阻尼因素，电路中引入综合等效电阻r。

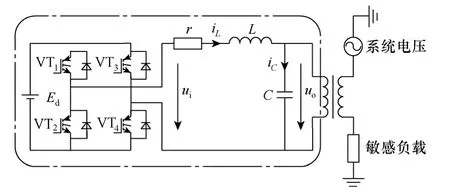
图1 单相H 桥逆变单元电路模型Fig.1 Circuit model of single-phase H-bridge inverter unit

选择补偿电压uo和滤波电感电流iL为状态变量；选择逆变单元输出电压ui和负载电流io为系统输入，可得状态空间表达式为

对应的连续时间模型如图2 所示

图2 单相H 桥逆变单元连续时间模型Fig.2 Continuous time model of single-phase H-bridge inverter unit

3 逆变单元数字比例谐振控制策略

为保证DVR 在非线性负载条件下能有更高质量的电压补偿效果，应设法提高其逆变单元对谐波电压的补偿能力。可以通过采用合理的数字控制方法，增强DVR 逆变单元抑制非线性负载扰动的能力，最大限度的限制非线性负载对输出电压的影响，减小输出波形的畸变。

由于数字处理器采样、计算延时的影响，PWM脉冲的更新一般需要滞后一拍采样时间[15]，对强调动态特性的DVR 来说，此影响不可忽略。数字控制技术的关键是选择合适的离散化方法，采用带零阶保持器（Zero-Order Holder，ZOH）的阶跃响应不变法对DVR 逆变单元的连续时间模型进行离散化，使系统的稳定性和增益保持不变。逆变单元开关器件的开关动作所引起的高次谐波可由LC 滤波器滤除，而非线性负载等因素产生的低次谐波只能通过合理的控制器设计来补偿。目前常见的非线性负载主要是含有滤波电容的整流型负载，此类负载使逆变单元输出的断续负载电流中含有大量的奇次谐波电流，流经输出阻抗造成电压波形畸变。因此，提出的双闭环数字控制策略包含了基波PR 控制电压外环以及含量较高的3 次、5 次和7 次指定谐波PR 控制电感电流内环，控制结构如图3 所示。其中Kp1和R1(z) 表示基波PR 控制器，Kph、R3(z)、R5(z)和R7(z)分别表示3 次、5 次和7 次谐波PR 控制器。

图3 双闭环数字PR 控制器Fig.3 Dual-loop digital PR controller

负载电流io中的低次谐波电流在H 桥逆变单元的连续时间模型中只是一种扰动，它经过1/Cs环节引起输出电压uo波形的畸变。电流内环谐波PR 控制器对逆变单元的控制作用抑制了低次谐波电流对系统的影响，保证了DVR 对电压跌落和谐波电压的快速精确补偿。

4 比例谐振控制器的离散化

PR 控制器是在谐振控制器的基础上增加了一个比例控制环节，在谐振频率处增益无穷大，而在非谐振频率处增益非常小，并且能够直接控制交流量，实现消除稳态误差的目的。

根据文献[16]的原则，PR 控制器的传递函数如式（2）所示。

式中，Kp为比例控制环节的比例系数；Kr为谐振系数；ωn为谐振角频率。

对于特定频率的PR 控制器来说，Kp只是一个常数，根据Z 变换的线性定理，实际上式（2）只需要对第二项谐振控制器进行离散化即可。对PR控制器离散化方法的讨论也就转化为对谐振控制器离散化方法的讨论，式（3）如下所示。

Kr仅仅是谐振系数，在讨论PR 控制器离散化方法的时候，可以将其忽略。对相角滞后进行补偿，式（3）可改写为

式中，θn为相角滞后补偿角。式（4）根据文献[15-17]中的虚拟LC 法来实现，输出方程可表示为

式中，I L(s)和U C(s)分别为虚拟LC 电路的电感电流和电容电压。

由于ωn为谐振频率处的角频率，故可将 1/ωn视为谐振系数Kr的一个因子来考虑，则虚拟LC 电路的输出式（5）可改写为

对式（6）离散化得到的离散输出方程为

式中，C=（cosθn-sinθn）。

虚拟LC 电路的离散时间状态方程为[15-17]

利用式（7）和式（8）得到的z域传递函数为

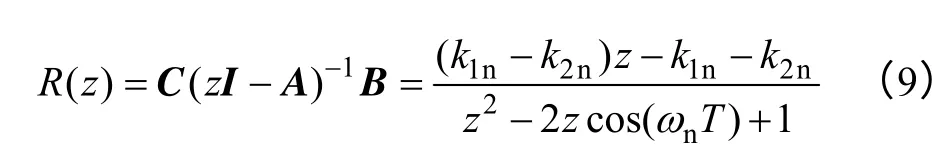
式中，k1n=cosθnsin(ωnT)；k2n=sinθn［1-cos(ωnT)］。

如果直接采用阶跃响应不变法对式（4）进行离散化可得

离散时间传递函数式（9）和式（10）相比，只是相当于扩大了ωn倍，这是因为式（5）中为了方便讨论虚拟LC 离散化方法，将1/ωn视为谐振系数Kr的一个因子造成的。

由以上分析可知，采用虚拟LC 法和阶跃响应不变法对谐振控制器进行离散化的效果是完全相同的，可以利用离散时间传递函数式（9）或式（10）来分析系统的稳定性和进行数字设计。因此，本文采用分析得到的离散化方法对PR 控制器进行设计。

5 控制策略分析及参数设计

5.1 电流内环

电流内环中的一拍延时z-1表示数字控制的采样、计算延时，此延时对着重强调稳态误差的逆变器来说可以忽略，但对动态响应速度要求更高的DVR 则有着至关重要的影响。因此，在分析控制系统性能和设计参数时引入了一拍延时，以求获得更接近于实际DVR 的控制性能和谐波补偿效果。

逆变单元的传递函数G(s) 可由图2 推导出

实验样机具体参数为L=680μ H，C=100μ F，r=0.2Ω，采样周期T=0.1ms，采用带ZOH 的阶跃响应不变法对G(s) 进行离散化，将其变换为z域传递函数G(z)。

电流内环的参数设计采用式（10）的离散化方法，3 次、5 次和7 次谐波经过一拍延时和LC 滤波后相角滞后分别约为42.5°、45°和47.5°，可得θ3=42.5°、θ5=45°以及θ7=47.5°。谐波谐振控制器的z域传递函数R3(z)、R5(z)和R7(z) 分别为

文献[18,19]提出了系统稳定性优先考虑的原则，当取Kph=0.9 时，DVR 控制系统稳定性良好。结合以上分析，可得电流内环的z域开环传递函数Gh(z) 为

电流内环开环传递函数Gh(z) 的伯德图如图4所示。通过分析幅频特性曲线可知电流内环在3 次、5 次和7 次谐振频率处的增益非常大，电流反馈可以有效抑制负载电流中的3 次、5 次和7 次谐波电流对DVR 补偿输出电压的影响。

图4 谐波比例谐振控制器伯德图Fig.4 Bode diagram of harmonic PR controller

5.2 电压外环

与电流内环类似，采用式（10）的虚拟LC 离散化方法对电压外环进行参数设计。基波经过一拍延时和LC 滤波后相角滞后约为40°，可得θ1=40°。基波谐振控制器的z域传递函数R1(z) 为

取Kp1=1.4 时，系统稳定。基波PR 控制器的z域传递函数PR1(z)为

将负载电流io看作电流内环的一种扰动，可得补偿电压uo的传递函数为

式（19）的第二项是电流内环“干扰量”io对补偿电压uo的影响，C(z) 为电容积分环节的z域传递函数。基波PR 控制器PR1(z)在基波频率ω0处的增益趋于无穷大，则第二项趋于0。同理，式（19）的第一项基本等于给定补偿电压ui。因此，基波PR控制器不但可以实现零稳态误差，还可以抑制负载电流对输出的影响。

6 实验结果

6.1 电压跌落及谐波补偿

为了验证提出的数字控制策略的正确性和有效性，开发了一台11kV·A 的DVR 样机，如图5 所示。检测控制单元采用TI 公司的DSP 芯片TMS320F2812和Altera 公司的FPGA 芯片EP1K30TC144。DSP完成PWM 脉冲信号输出和驱动保护等功能，FPGA则负责信号采集以及数字控制等。下表为DVR 样机的实验参数。

图5 DVR 样机Fig.5 DVR experimental prototype

表 DVR 样机的实验参数Tab.Experiment parameters of DVR

DVR 样机除了能补偿电压跌落以外，还可以补偿负载电压的谐波。为此对DVR 样机进行单独补偿谐波实验和补偿电压跌落及谐波的综合实验。图6a是非线性负载投入时的负载电压电流波形，非线性负载的投入使得负载电压发生畸变。由图6b 可知负载电压主要含有3 次、5 次和7 次等低次谐波，总谐波畸变率（Total Harmonic Distortion，THD）为36.28%，其中3 次谐波畸变率为13.25%，5 次谐波畸变率为11.37%，7 次谐波畸变率为7.82%，低次谐波含量较高。

图6 负载投入时的电压电流波形及电压频谱图Fig.6 Voltage current waveform and voltage spectrum under load

负载电压中3 次、5 次和7 次谐波电压的含量最高，因此DVR 样机主要针对3 次、5 次和7 次谐波电压进行补偿。图7是负载电压正常时投入非线性负载，DVR 样机仅对谐波电压进行补偿的效果。经过DVR 样机的补偿后，3 次谐波畸变率由13.25%降低到 0.58%，5 次谐波畸变率由 11.37%降低到0.46%，7 次谐波畸变率由7.82%降低到0.75%，3次、5 次和7 次谐波含量均在合格范围之内，THD也由原来的36.28%降低到4.69%。

图7 谐波电压补偿效果Fig.7 Compensation effect for voltage harmonics

图8是负载电压发生跌落时投入非线性负载，DVR 样机对电压跌落及谐波的补偿效果。此时，负载电压稳定在220V±0.7V，稳态精度为0.32%。3 次谐波畸变率由13.25%降低到0.93%，5 次谐波畸变率由11.37%降低到0.57%，7 次谐波畸变率由7.82%降低到0.83%，经过补偿后的负载电压中3 次、5 次和7 次谐波含量大大减小。由此可见，本文提出的控制策略在稳态时对电压跌落及谐波电压具有良好的补偿效果。

图8 电压跌落及谐波电压补偿效果Fig.8 Compensation effect for voltage sag and harmonics

6.2 动态响应实验

DVR 样机的控制策略不同于只强调稳态响应的电力有源滤波器，不但要有精确的基波电压补偿能力，而且要消除3 次、5 次和7 次等低次谐波电压，不但强调稳态精度更看重动态响应速度。电压跌落和恢复正常时的负载电压波形如图9 所示，可见DVR 样机的动态响应时间约为3ms 左右，可以快速地动态补偿电压跌落和指定次谐波电压。

7 结论

在保证DVR 逆变单元动态响应特性的同时，为了使其能够补偿死区时间及非线性负载等因素产生的低次谐波，提出了一种新型的双闭环数字PR控制策略。在分析现有文献中PR 控制器离散化方法的基础上，得出了虚拟LC 法和阶跃响应不变法的离散效果相同的重要结论，并根据最后计算出的离散时间传递函数直接对基波PR 控制器以及3 次、5 次和7 次谐波PR 控制器进行数字设计。在分析控制系统性能和设计参数时引入了一拍延时，减小了数字处理器采样、计算延时等的影响，获得了更接近于实际DVR 的控制性能和谐波补偿效果。基于本文提出的控制策略及数字设计方法已应用于开发的DVR 样机中，在非线性负载投入时，不仅使负载基波电压保持稳定，而且还可以有效抑制特定次负载谐波电流对DVR 输出电压的影响，使电压质量满足用户要求。

[1]Ho C N,Chung H S.Implementation and performance evaluation of a fast dynamic control scheme for capacitor-supported interline DVR[J].IEEE Transactions on Power Electronics,2010,25(8):1975-1988.

[2]Mostafa I,Ayman B,Ahmed A E.An energy optimized control scheme for a transformerless DVR[J].Electric Power Systems Research,2012,83(1):110-118.

[3]申科,王建赜,蔡兴国,等.动态电压恢复器比例谐振控制[J].电力自动化设备,2010,30(7):65-69.Shen Ke,Wang Jianze,Cai Xingguo,et al.Proportional resonant control for dynamic voltage restorer[J].Electric Power Automation Equipment,2010,30(7):65-69.

[4]王智勇,吴正国,周卫平,等.基于基波特征量提取的DVR 参考电压波形生成算法[J].电工技术学报,2009,24(4):168-174.Wang Zhiyong,Wu Zhengguo,Zhou Weiping,et al.A novel reference wave generating algorithm based on characteristic vector extracted for DVR[J].Transactions of China Electrotechnical Society,2009,24(4):168-174.

[5]Vilathgamuwa M,Ranjith Perera A A D,Choi S S.Performance improvement of the dynamic voltage restorer with closed-loop load voltage and currentmode control[J].IEEE Transactions on Power Electronics,2002,17(5):824-834.

[6]Nielsen J G,Newman M,Nielsen H,et al.Control and testing of a dynamic voltage restorer(DVR) at medium voltage level[J].IEEE Transactions on Power Electronic,2004,19(3):806-813.

[7]王同勋,薛禹胜,Choi S S.动态电压恢复器研究综述[J].电力系统自动化,2007,31(9):101-107.Wang Tongxun,Xue Yusheng,Choi S S.Review of dynamic voltage restorer[J].Automation of Electric Power Systems,2007,31(9):101-107.

[8]Jenopaul P,Deva Prakash T R,Raglend I J.Power quality improvement for matrix converter using unified power quality conditioner[J].Transactions of the Institute of Measurement and Control,2012,34(5):585-593.

[9]Moradlou M,Karshenas H R.Design strategy for optimum rating selection of interline DVR[J].IEEE Transactions on Power Delivery,2011,26(1):242-249.

[10]Roncero Sanchez P,Acha E,Ortega Calderon J E,et al.A versatile control scheme for a dynamic voltage restorer for power-quality improvement[J].IEEE Transactions on Power Delivery,2009,24(1):277-284.

[11]Goharrizi A Y,Hosseini S H,Sabahi M,et al.Three-phase HFL-DVR with independently controlled phases[J].IEEE Transactions on Power Electronics,2012,27(4):1706-1718.

[12]杨秋霞,梁雄国,郭小强,等.准谐振控制器在有源电力滤波器中的应用[J].电工技术学报,2009,24(7):171-176.Yang Qiuxia,Liang Xiongguo,Guo Xiaoqiang,et al.Application of quasi resonant controller for active power filter[J].Transactions of China Electrotechnical Society,2009,24(7):171-176.

[13]黄朝霞,邹旭东,童力,等.基于极点配置和重复控制的电流型单相动态电压调节器[J].电工技术学报,2012,27(6):252-260.Huang Zhaoxia,Zou Xudong,Tong Li,et al.Research on current control mode single-phase dynamic voltage regulator based on pole-assignment and repetitive control[J].Transactions of China Electrotechnical Society,2012,27(6):252-260.

[14]胡磊磊,肖国春,滕国飞,等.基于等效基波及奇次谐波谐振器组的单相动态电压恢复器控制[J].中国电机工程学报,2012,32(22):104-112.Hu Leilei,Xiao Guochun,Teng guofei,et al.An equivalent fundamental and odd harmonic resonators controller for a single-phase dynamic voltage restorer[J].Proceeding of the CSEE,2012,32(22):104-112.

[15]李子欣,王平,李耀华,等.采用数字控制的400Hz大功率逆变电源[J].中国电机工程学报,2009,29(6):36-42.Li Zixin,Wang Ping,Li Yaohua,et al.400Hz highpower voltage source inverter with digital control[J].Proceeding of the CSEE,2009,29(6):36-42.

[16]Mihalache L.Improved load disturbance rejection method for 400 Hz GPU inverters[C].The 19th Annual IEEE Applied Power Electronics Conference and Exposition,USA,2004,1:95-101.

[17]Mihalache L.DSP control of 400 Hz inverters for aircraft applications[C].The 37th IAS Annual Meeting and World Conference on Industrial Applications of Electrical Energy,USA,2002,3:1564-1571.

[18]Bojoi R I,Griva G,Bostan V,et al.Current control strategy for power conditioners using sinusoidal signal integrators in synchronous reference frame[J].IEEE Transactions on Power Electronics,2005,20(6):1402-1412.

[19]Liserre M,Teodorescu R,Blaabjerg F.Double harmonic control for three-phase systems with the use of resonant current controllers in a rotating frame[J].IEEE Transactions on Power Electronics,2006,21(3):836-841.