基于电压崩溃指数的极限传输容量实用计算方法

姜 臻 苗世洪 尚亚男 侯俊贤 于之虹

（1.华中科技大学强电磁工程与新技术国家重点实验室 武汉 430074 2.中国电力科学研究院 北京 100192）

1 引言

随着我国长距离、大容量输电的出现和逐步发展，输电距离长、供电范围大是我国大电网发展过程中的主要特点，这使得我国主干输电线的输送能力主要取决于线路的极限传输容量[1]。在这种环境下，极限传输容量问题已经成为电力系统运行的重要评估指标之一。北美电力可靠性委员会在20 世纪90 年代提出了电网可用输电能力（Available Transfer Capability,ATC）的概念[2]，定义ATC 为在已有的协议基础上，在实际输电网中可用于进一步商业活动的剩余输电能力。而要计算ATC 就必须先计算系统极限传输容量（Total Transfer Capability,TTC）。显然，如何准确地计算TTC，是电力市场环境下电力系统分析中的一个基本任务，同时，如何快速地计算TTC，更是大电网环境下输电系统安全稳定运行环节中迫切需要解决的关键问题。

目前求解系统极限传输容量的主要方法是连续性潮流（Continuation Power Flow,CPF）计算方法[3-8]，它通过在常规潮流方程中添加连续性参数，克服了常规潮流计算方法（如牛顿法等）在潮流解曲线鞍型分叉点处由于常规雅可比矩阵奇异而导致的计算困难，它考虑了系统的电压、无功及其他非线性安全因素影响，具有相当的准确性，非常适合极限传输容量的计算。自从连续潮流问题被提出以来，它在电力系统静态稳定性评估和系统极限传输容量计算等方面得到了广泛的应用。

但是由于CPF 方法需要从当前运行点开始逐渐增加负荷，逐步计算到系统的电压稳定临界点，计算通常比较耗时。而且在CPF 计算过程中，步长的选择是影响计算效率的关键因素之一。步长过小将会使计算效率大大降低，步长过大则有可能影响计算的收敛性[9-12]。此外，在CPF 计算中，常会遇到计算失败的情况，即CPF 的校正环节计算发散，具体表现为此时无论如何减小步长，校正计算都无法收敛。分析表明造成CPF 计算失败的原因是扩展雅可比矩阵奇异，而决定扩展雅可比矩阵性态的关键因素是CPF 所采用的参数化方法[13,14]。

系统极限传输容量是反映大电网环境下输电系统安全稳定的重要指标，由它可以直观地反映当前系统运行状态与稳定极限的接近程度。求解系统极限传输容量并不需要计算出完整的PV 曲线。在求解过程中，当系统薄弱环节到达电压拐点时，整个计算的任务就完成了，通过对此时系统状态的评价即可求得系统的极限传输容量[15-17]。事实上，系统在不同的运行状态或故障状态下将有不同的极限传输容量，在任何状态下都保持适当的负荷裕度才可以保持系统的电压稳定和电网的安全运行[18,19]，因此，系统极限传输容量的快速、实时求解拥有极高的实用价值和意义。

本文针对当前系统极限传输容量计算还存在的若干问题，提出了一种基于电压崩溃指数的极限传输容量计算模型和实用化算法。该方法以原始牛顿法为潮流计算核心，略去参数化方程，从而不会出现连续潮流扩展雅可比矩阵奇异造成CPF 计算失败的现象，同时，根据雅可比矩阵信息计算相应的电压崩溃指数，该参数可以引导整个潮流推演过程，将系统负荷（或发电）状态准确定位至功率极限点，此外，雅可比矩阵信息还可以自动选取合适的潮流推演步长，确保全网负荷（和发电）变化能够快速、准确地向系统极限点逼近。整个推演过程以雅可比矩阵为计算核心，不需要每步推演都有完整的牛顿迭代过程，从而使算法总体计算速度大幅提升。对诸多系统的数值计算表明，该方法在保证计算结果准确性的前提下具有较高的计算效率。

2 计算模型

2.1 潮流计算模型

潮流计算方程为

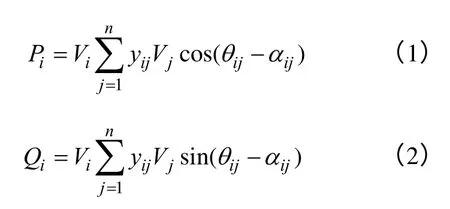
式中，yij和αij为节点导纳矩阵元素的幅值和相角，且Yij=yij∠αij=Gij+jBij。

在有n个节点的系统中，假定第1～m号节点为PQ 节点，第m+1～n-1 号节点为PV 节点，第n号节点为平衡节点。将方程组（1）和（2）线性化后，得到方程组

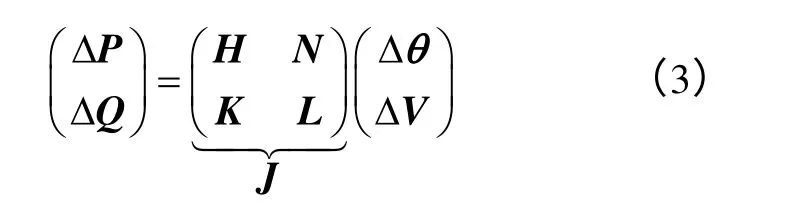
式中，H是(n-1)×(n-1)阶方阵；N是(n-1)×m阶方阵；K是m×(n-1)阶方阵；L是m×m阶方阵；J是(n+m-1)×(n+m-1)阶雅可比矩阵。

2.2 负荷增长模式

负荷的增长方式视功率交换方案而定，其中最简单的负荷增长方式为区域比例负荷增长方式,其定义如下[8,16]：考虑具有NL个节点的负荷变化区，假定各节点负荷为PiL+jQiL（i=1,2,…,NL），负荷变化区各节点负荷总和为

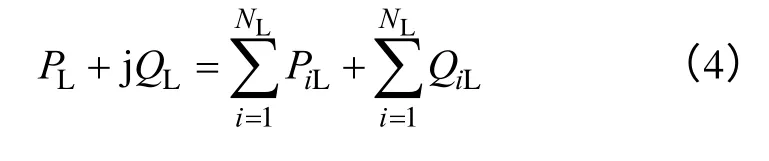
当总有功负荷增量为ΔPL时，各节点负荷的变化规律若按式（5）所定义即为区域比例负荷增长方式

式中，ΔPiL表示各节点有功负荷增量；φi为各节点负荷增长功率因数角。

当系统有功负荷增长时，仅由平衡机提供额外发电功率是不现实的，一般同时需要增大系统中可调节机组的有功功率以平衡需求。为此，考虑发电机有功出力调节方式对于系统极限传输容量的求取具有实际意义。本文考虑按比例分配方式调节发电机的有功出力。比例分配方式下各发电机参与有功调节所分配的功率增量与其当前有功输出成正比，即

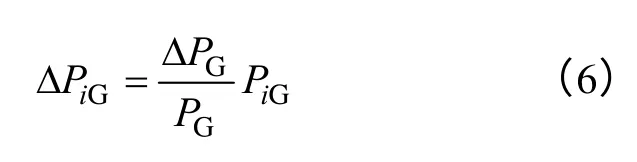
式中，ΔPiG、ΔPG分别表示各发电机以及总的有功输出增量；PiG、PG分别表示各发电机以及总的有功输出；NG为尚有调节能力的发电机数，i=1,2,…,NG。为保持有功平衡，在忽略网损变化的情况下，发电机有功功率的变化量应近似等于负荷变化量，即ΔPG=ΔPL。

区域比例负荷增长方式和发电机有功出力比例分配方式在计算中并不进行发电和负荷功率的优化分布，因而其求解过程简单、迅速，同时按此方式得到的极限传输容量结果也是相对保守的[19]。但是系统在不同的运行状态有不同的极限传输容量，尤其是在故障状态下系统极限传输容量较工况下更小。因此，在任何状态下都应保持适当的传输容量裕度才可以保持电网的安全稳定运行，所以，在保证计算结果准确性的前提下，系统极限传输容量的快速、实时求解更有实用价值和意义。

2.3 状态推演

连续潮流法被应用于电力系统从稳定平衡状态到稳定极限状态的推演过程，它的计算模型如下：

式中，x表示系统状态变量；λ表示系统参数,它主要用于系统状态的动态转变，一般来说，λ可以由负荷/发电机运行水平等系统参数量化而成。连续潮流的计算过程包括两个步骤：预测过程和矫正过程。

在连续潮流计算过程中，常常会遇到计算失败的情况，即CPF 在校正环节计算发散，具体表现为此时无论如何减小步长，校正计算都无法收敛，这一现象在计算穿越临界点前后都可能遇到。如果当计算穿越临界点后，在计算曲线的下半分支遇到计算发散，这时只是无法得到完整的PV 曲线，而并不影响极限传输容量的计算和精确临界点的求取。但如果在曲线的上半分支上计算发散，将无法得到确切的极限传输容量及其临界点。文献[13,14]分析表明造成CPF 计算失败的原因是扩展雅可比矩阵奇异，而决定扩展雅可比矩阵性态的关键因素是CPF所采用的参数化方法。针对这个问题，本文在状态推演中将以原始牛顿法为潮流计算核心，略去参数化方程，从而避免连续潮流扩展雅可比矩阵奇异造成CPF 计算失败的问题，进而减少连续潮流计算过程中鲁棒性控制的时间成本，节约计算时间。

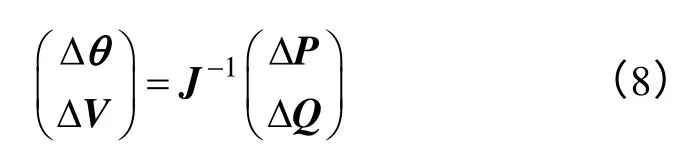
将负荷增长模式量化为λ，λ即是每步状态推演的预测步长Δλ之和，因此，推演状态的节点注入有功、无功向量计算如下：

式中，P0、Q0分别表示基态节点注入有功、无功向量。由式（9）和式（10）可推得有功、无功增量方程如下：

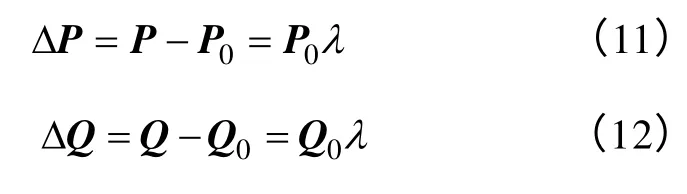
因此，状态推演的正切向量TV定义为

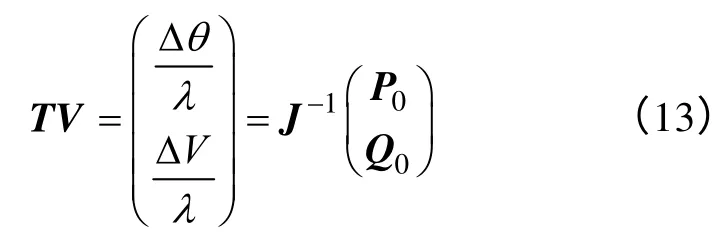
同时，状态推演的预测步长采用形式[20]为

式中，|| ·|| 表示欧几里德范数；k为一个加速或减速步长推演的加速比标量。

由于状态推演过程需要由当前运行点开始逐渐增加负荷，逐步计算到系统的电压稳定临界点，计算通常是比较耗时的，而且在计算过程中，步长的选择是影响计算效率的关键因素之一，步长过小将会使计算效率大大降低，步长过大则有可能影响计算的收敛性。本文所采用的状态推演步长Δλ（见式（14））有自动调节的功能，即在距离稳定临界点较远的系统状态下步长较大，而在距离临界点较近的系统状态下步长较小。随着PV 曲线临近临界点，雅可比矩阵J将出现主特征值为0 的现象，根据式（13）可知，此时正切向量TV的欧几里德范数理论上将趋近无穷大，也就是说，当系统状态临近临界点时，预测步长Δλ将逐渐减小直至为0。因此，该步长推演同时兼顾了计算的时间效率和准确性，仿真分析验证了其这个特点。

3 电压崩溃指数

根据式（13）、式（14）可知，在临界点附近，预测步长较小，此时则可能出现在临界点附近状态推演次数过多的现象。因此，为了更好地反映PV曲线逼近临界点的趋势，同时，也是为了减少在临界点附近状态推演次数，减小式（13）、式（14）中求解J-1和||TV|| 的计算量，需要设计一个参数来引导整个状态推演过程准确、快速地向临界点推进。

对于环境要素(见图1),事件e2的发生地点同时也是事件e3和事件e4的发生地点,这时就要在事件e2的环境要素属性lid中进行标注.

实际上，求解系统极限传输容量并不需要描绘出完整的PV 曲线，PV 曲线的上半支曲线才是有意义的。如图1 所示，当曲线到达临界点的时候，整个状态推演和潮流计算的任务就完成了，通过对此时系统状态（节点电压及功角）进行分析，即可以求得系统极限传输容量。因此，如何准确、快速地将整个状态推演过程及系统负荷（和发电）状态准确引导并定位至功率极限点（临界点）是至关重要的。

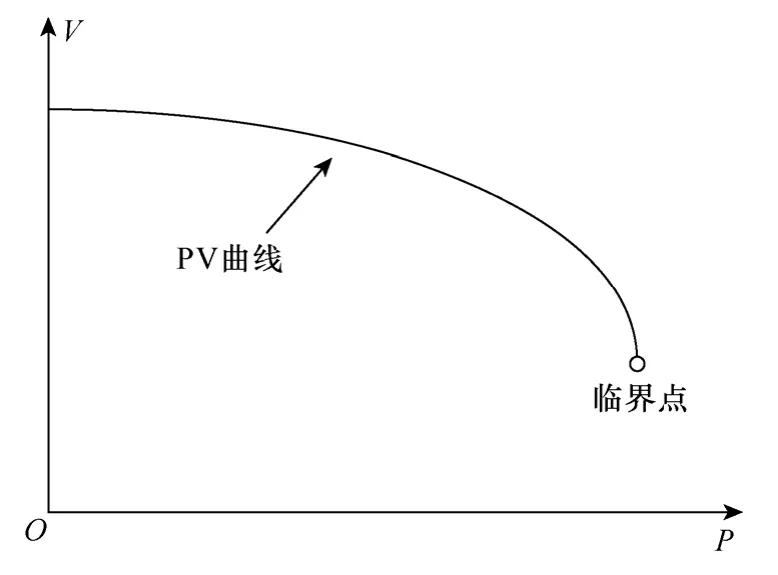
图1 PV 曲线示意图Fig.1 Schematic diagram of PV curve

当PV 曲线接近临界点时，用于评价雅可比矩阵主特征值的电压崩溃指数IC将趋近为0[21]。其中电压崩溃指数IC定义为

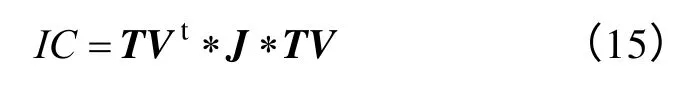
式中，TV表示状态推演的正切向量，上标t 表示相量的转置；J为雅可比矩阵。定义状态推演结束判据如下：

式中，ICset为电压崩溃指数门槛值，当电压崩溃指数IC持续下降并小于该门槛值时，表明当前系统状态可以近似为临界点状态，整个状态推演过程即可结束。设置该判据可以避免因在临界点附近预测步长较小而出现状态推演次数过多的现象，同时，也可以改善因为推演次数过多而造成的求解J-1和||TV|| 的低时间效率问题。

4 流程分析

4.1 系统极限传输容量计算流程

根据前述分析可知，基于电压崩溃指数的极限传输容量计算流程如下：

（1）根据在线数据计算系统初始潮流，并依据牛顿法最后一次迭代的雅可比矩阵J求解初始的状态推演正切向量TV、预测步长Δλ以及电压崩溃指数IC。

（2）对潮流解进行静态安全约束校验。如不满足约束校验，则直接进入系统极限传输容量评估模块，如满足约束校验，则进入下一个流程。

（3）对所求解的电压崩溃指数IC按照判据（16）进行评估。当满足判据时，表明所推演的系统状态已经接近系统临界点，即停止推演，进入极限传输容量评估模块，如果不满足判据，则进入下一个流程，继续状态推演计算。

（4）状态推演过程。根据前一步推演所得的预测步长Δλ在前一个推演状态下增加负荷，并根据潮流计算求解出新的推演状态点，同时，更新相应的正切向量TV、预测步长Δλ以及电压崩溃指数IC数值，并进入流程（2）的计算，直至状态推演过程结束。

完整的极限传输容量计算流程如图2 所示。

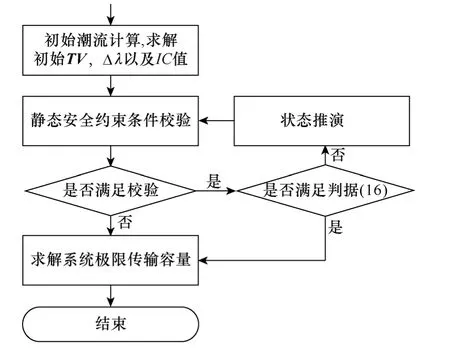
图2 基于电压崩溃指数的极限传输容量计算流程Fig.2 Flow chart of voltage collapse indices based method for computation of total transfer capability

4.2 简化计算流程

根据式（13）～式（15）可知，状态推演过程中正切向量TV、预测步长Δλ以及电压崩溃指数IC的计算都离不开牛顿雅可比矩阵，因此，整个状态推演过程以雅可比矩阵为计算核心。然而，牛顿潮流每次迭代都会生成相应的雅可比矩阵，因此在计算TV、Δλ以及IC时并不需要每步推演都有完整的牛顿迭代过程，理论上只要进行一次牛顿迭代即可评估相应的TV、Δλ和IC值。当电压崩溃指数IC满足状态推演判据（16）后，进行一次完整的牛顿潮流计算即可完成系统极限传输容量的评估。

随着系统状态向临界点推进，完整法牛顿迭代之后的雅可比矩阵J会出现主特征值为0 的现象，也即是说，利用完整法是可以保证电压崩溃指数收敛至0 及系统状态收敛至临界状态点的。由此可见，系统状态本身就包含了雅可比矩阵主特征值的信息，即系统状态向临界点推进的同时，雅可比矩阵主特征值也在向0 收敛。由于简化法在中间系统状态下只进行一次雅可比矩阵计算，雅可比矩阵收敛程度不高，其主特征值向0 收敛的速率较完整法会小一些，尽管如此，由于系统状态向临界点的推进，雅可比矩阵主特征值向 0 收敛的趋势是不会改变的，这就是利用简化法也能保证系统状态收敛至临界状态点的原因。

由于不用在每一步的状态推演中进行繁琐的牛顿迭代，这种简化算法可以大幅提升系统临界点极限传输容量的计算速度，但也正因在中间的状态推演过程中没有完整的牛顿迭代，这种计算是无法保证所有中间推演状态满足系统静态安全约束条件的。尽管如此，由于这种推演计算求解过程简单、迅速，并且能实时、准确反映系统临界点的传输容量，即理论上的系统极限容量，因而这种推演算法在快速、实时评估电网的安全稳定裕度领域依然有极高的实用价值和意义。

基于电压崩溃指数的极限传输容量简化计算流程如图3 所示，仿真分析验证了该方法的有效性。

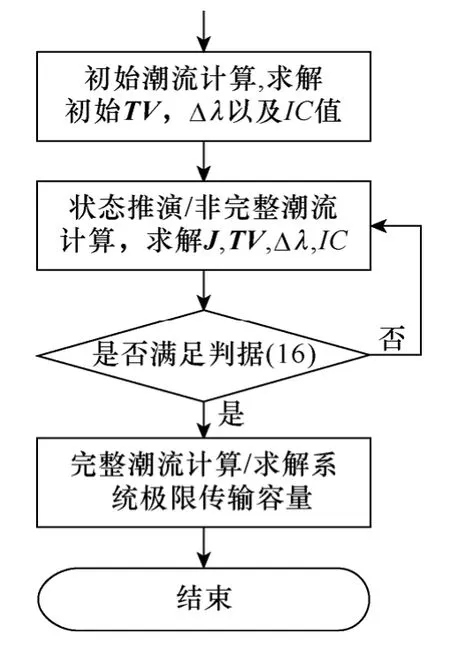
图3 基于电压崩溃指数的极限传输容量简化计算流程Fig.3 Flow chart of voltage collapse indices based simplified method for practical computation of total transfer capability

5 算例分析

5.1 新英格兰机39 节点系统算例分析

为验证本文所提出系统极限传输容量算法的有效性，将本文提出的方法对新英格兰10 机39 节点系统进行了分析计算，该系统基准电压为100kV，基准功率为100MV·A。如图4 所示，取节点17-16，4-14，6-11 之间的联络线进行系统分解，将该系统分为A、B 两个区域。区域A 有5 台发电机和12个负荷节点，区域 A 的总发电量和总负荷分别为3 255MV·A、3 982.5MW；区域B 包括5 台发电机和7 个负荷节点，区域B 的总发电量和总负荷分别为3 097.5MV·A、2 167.6MW。因此，系统基态情况下，区域B 需要向区域A 输送功率。

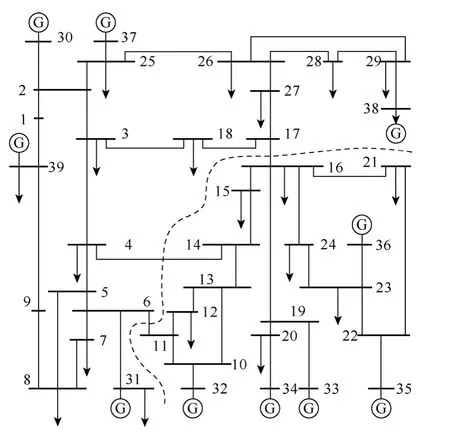
图4 新英格兰39 节点系统Fig.4 New England 39-bus system

当状态推演的预测步长加速比k设置为0.1 时，预测步长较小，按照完整极限传输容量计算流程（下文简称为完整法）、简化极限传输容量计算流程（下文简称为简化法）以及传统连续潮流法（下文简称为传统法）计算所得输电断面7-16，4-14，6-11 的极限传输容量见表1，结果显示完整法、简化法以及传统法所求得的结果非常接近，从而验证了基于电压崩溃指数的极限传输容量算法的有效性。

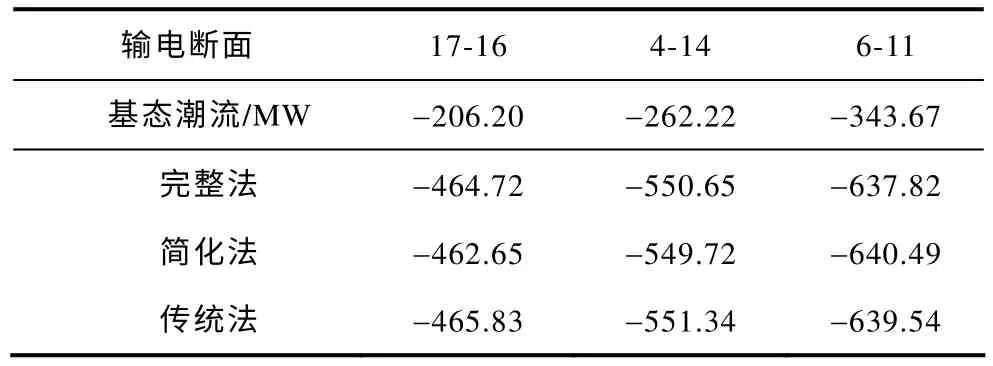
表1 三种方法的极限传输容量结果Tab.1 Total transfer capability results of three method s

利用完整法所求的系统关键站点4 的PV 曲线上半支曲线如图5 所示，系统状态经过31 次推演达到临界点。同时，电压崩溃指数IC随同负荷增长模式量化参数λ变化曲线如图6 所示，由该曲线可以看出，当完整法完成初始潮流计算之后，第一个电压崩溃系数IC才出现，这符合图2 完整法的计算流程。当电压崩溃指数IC满足判据（16）时，即IC接近0 时，状态推演所得的PV 曲线也达到了系统临界点。此外，该曲线还显示状态推演步长在距离稳定临界点较远的系统状态下步长较大，而在距离临界点较近的系统状态下步长较小，具有自适应条件功能，符合前述的理论分析。

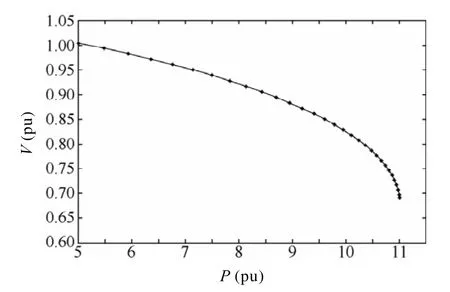
图5 完整法追踪的站点4 PV 曲线Fig.5 PV curve of bus 4 tracked by intact method

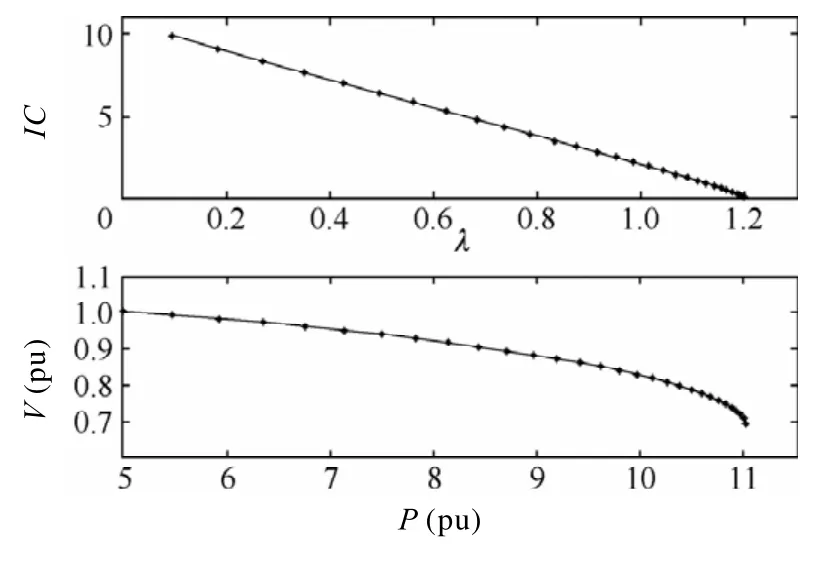
图6 完整法跟踪的站点4 的IC-λ曲线Fig.6 IC-λ curve of bus 4 tracked by intact method

图7 显示了基于电压崩溃指数的极限传输容量完整法与传统算法的PV 曲线计算结果对比图。由于传统法没有依赖电压崩溃指数IC的引导，必须描绘一条完整的PV 曲线才能求取系统的功率极限点，并且其在功率极限点附近不具有状态推演密集的自适应调节功能。本算例中，新算法推演次数为 31次，计算总时间为0.801s，而传统法推演次数为65次，计算总时间为5.377s，因此，新算法在计算速度上优势明显。同时，图7 也显示了新算法与传统算法所求解的功率极限点结果非常接近。

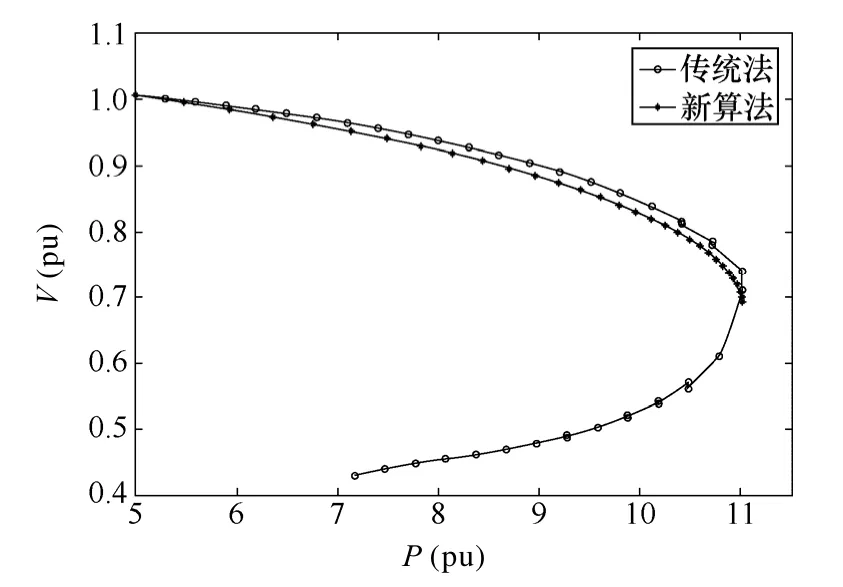
图7 传统法与新算法的结果对比Fig.7 Results comparison of the traditional method and the novel algorithm

由于简化法不用在每一步的状态推演中进行繁琐的牛顿迭代，所以简化法是无法描绘状态推演过程中的PV 曲线的。图8 显示的是预测步长加速比k为0.1 时的系统关键站点4 的IC-λ曲线。由于状态推演在中间状态的牛顿计算中没有进行充分的迭代，所以提取用于求取正切相量TV、预测步长Δλ以及电压崩溃指数IC的雅可比矩阵J中的主特征值相对较大，进而造成状态推演过程中电压崩溃指数IC衰减的速率也会相应降低，因此，相较于完整法，简化法的状态推演次数更多。以输电断面4-14为例，分别采用完整法和简化法对不同预测步长加速比k所求极限传输容量及状态推演次数的结果进行对比，其结果见表2。表2 的结果显示：①同种加速比下，简化法推演次数较完整法更多，符合前述分析；②预测步长加速比越大，推演次数越少，符合实际情况；③预测步长加速比越大，相应的极限传输容量结果越趋于保守，但总体上计算精度较高。

图8 简化法跟踪的IC-λ曲线Fig.8 IC-λ curve of bus 4 tracked by simplified method

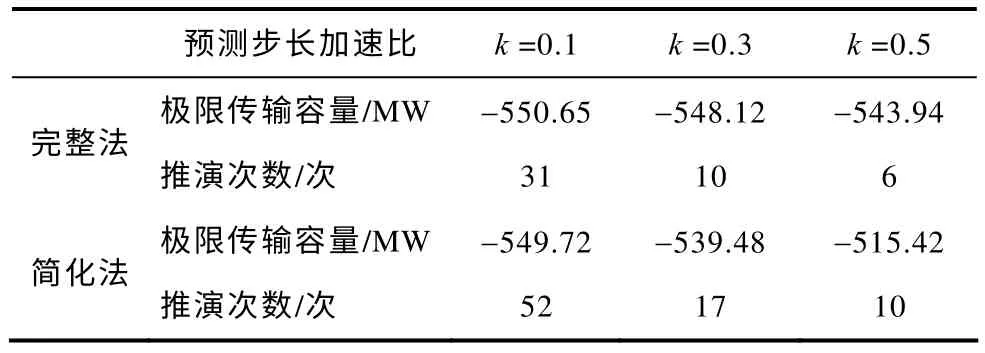
表2 两种方法在不同预测步长加速比下的结果对比Tab.2 Results in different prediction step sizes accelerated ratio two methods

之所以采用简化法，是由于这种推演计算求解过程简单、迅速，并且能实时、准确地反映系统临界点的传输容量。然而简化法表现出比完整法更多的推演次数却并不会增加极限传输容量的总体计算时间，下面一节将详细分析两种算法的计算时间效率。

5.2 计算时间效率分析

为分析本文所提出系统极限传输容量算法（完整法和简化法）的计算时间效率，将本文提出的两种方法以及传统法对IEEE 30、New England 39、IEEE 57、IEEE 118 及IEEE 300 节点系统进行分析计算。表3～表5 分别提供了预测步长加速比为0.1、0.3和0.5 时的完整法和简化法计算时间分析结果。传统法对此五个系统的运算时间分别为 5.261s、5.377s、18.967s、35.734s和114.542s。从该结果中可得出如下结论：

（1）简化法较完整法推演次数更多，但总体计算时间较少，原因是简化法在推演系统中间状态过程中不进行完整的牛顿迭代计算，因此虽然简化法推演次数较多，但总体计算时间较完整法还是减少了。

（2）加速比越大，系统状态推演次数和算法总体计算时间越小。

（3）对于不同的系统模型，通过选择合适的预测步长加速比k，可以达到在确保准确计算的前提下快速求解极限传输容量的目的。

（4）当系统节点较多，拓扑较为复杂的情况下，虽然简化法无法校验静态安全约束条件，但其在反映系统临界点的传输容量上拥有性能优良的时间优势。

（5）新算法，即完整法和简化法在计算速度上较之传统法都更加快速，时间优势明显。

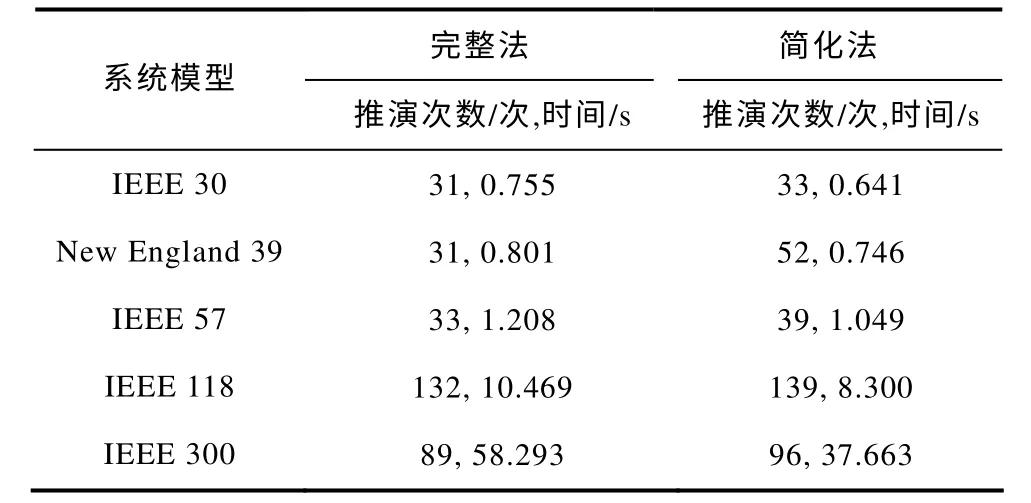
表3 加速比k 为0.1 的时间分析结果Tab.3 Time analysis results when accelerated ratio is set as 0.1

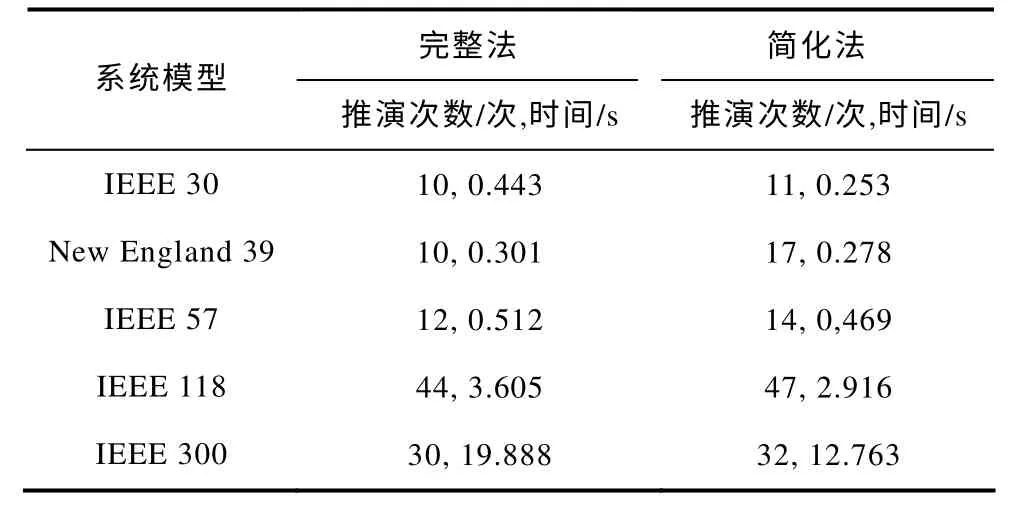
表4 加速比k 为0.3 的时间分析结果Tab.4 Time analysis results when accelerated ratio is set as 0.3

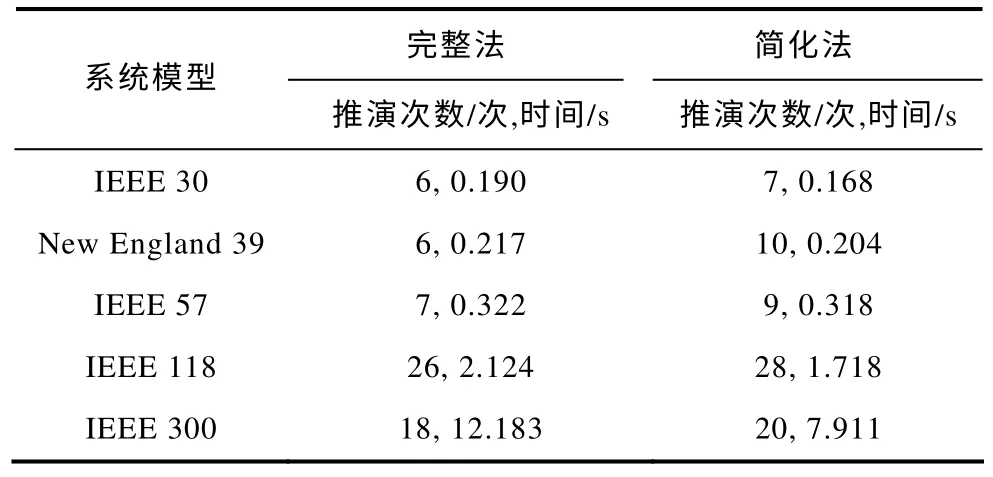
表5 加速比k 为0.5 的时间分析结果Tab.5 Time analysis results when accelerated ratio is set as 0.5

6 结论

本文针对目前系统极限传输容量计算还存在的若干问题，提出了一种基于电压崩溃指数的极限传输容量计算模型和实用化算法。该方法以原始牛顿法为潮流计算核心，略去参数化方程，避免了扩展雅可比矩阵奇异造成连续潮流计算失败的现象，同时，根据雅可比矩阵信息计算相应的电压崩溃指数引导整个状态推演过程，将系统负荷（或发电）状态快速、准确定位至功率极限点，此外，该算法还可以自动选取合适的状态推演步长，确保全网负荷（和发电）变化能够快速、准确地向系统极限点逼近。对诸多系统的数值分析表明，该算法在保证计算结果准确性的前提下具有较高的计算效率，具有极高的实用价值。

[1]周孝信,郭剑波,胡学浩,等.提高交流500 kV 线路输电能力的实用化技术和措施[J].电网技术,2001,25(3):1-6.Zhou Xiaoxin,Guo Jianbo,Hu Xuehao,et al.Engineering technologies and measures for improving the transmitting capability of 500kV transmission lines[J].Power System Technology,2001,25(3):1-6.

[2]North American Electric Reliability Council.Available transfer capability definitions and determination:A reference document prepared by TTC task force[R].New Jersey:North American Electric Reliability Council,1996.

[3]Ilic M D,Yoon Y T,Zobian A.Available transmission capacity(ATC) and its value under open access[J].IEEE Transactions on Power Systems,1997,12(2):636-645.

[4]Li W,Liu H,Yan Z,et al.ATC calculation with steadystate security constraints using Benders decomposition[J].IEE Proceedings-Generation,Transmission and Distribution,2003,150(5):611-615.

[5]吴杰康,周举,吴强,等.基于小干扰稳定约束可用传输容量的计算[J].电工技术学报,2006,21(9):7-12.Wu Jiekang,Zhou Ju,Wu Qiang,et al.Available transfer capability calculation with small signal stability constraints[J].Transactions of China Electrotechnical Society,2006,21(9):7-12.

[6]周明,谌中杰,李庚银,等.基于功率增长优化模式的交直流电网可用输电能力计算[J].中国电机工程学报,2011,31(22):48-55.Zhou Ming,Chen Zhongjie,Li Gengyin,et al.Available transfer capability determination for AC/DC transmission systems based on power increase optimization mode[J].Proceedings of the CSEE,2011,31(22),48-55.

[7]郭琦,赵晋泉,张伯明,等.一种线路极限传输容量的在线计算方法[J].中国电机工程学报,2006,26(5):1-5.Guo Qi,Zhao Jinquan,Zhang Boming,et al.A method for on-line computation of total transfer capability[J].Proceedings of the CSEE,2006,26(5):1-5.

[8]赵晋泉,张伯明.连续潮流及其在电力系统静态稳定分析中的应用[J].电力系统自动化,2005,29(11):91-97.Zhao Jinquan,Zhang Boming.Summarization of continuation power flow and its applications in static analysis of power system[J].Automation of Electric Power Systems,2005,29(11):91-97.

[9]Taylor G,Irving M.Performance analysis of a novel q-limit guided continuation power flow method[J].IET Generation,Transmission &Distribution,2009,3(12):1042-1051.

[10]Mohn F W,de Souza A C Z.On fast decoupled continuation power flows[J].Electric Power Systems Research,2002,63(2):105-111.

[11]王成山,魏炜.一种改进的步长控制连续性潮流计算方法[J].电工技术学报,2004,19(2):58-63.Wang Chengshan,Wei Wei.An improved continuation method with controlled step size[J].Transactions of China Electrotechnical Society,2004,19(2):58-63.

[12]董晓明,梁军,韩学山,等.连续潮流参数选择及步长控制的分析与改进[J].电力系统自动化,2011,35(13):49-53.Dong Xiaoming,Liang Jun,Han Xueshan,et al.Analysis and improvement on parameter selection strategy and step size controlling in continuation power flow[J].Automation of Electric Power Systems,2011,35(13):49-53.

[13]Alves,D.A.,da Silva,L.C.P.,Castro,C.A.,et al.Continuation fast decoupled power flow with secant predictor[J].IEEE Transactions on Power Systems,2003,18(3):1078-1085.

[14]赵晋全,张伯明.改进连续潮流计算鲁棒性的策略研究[J].中国电机工程学报,2005,25(22):7-11.Zhao Jinquan,Zhang Boming.A study on the strategy for improving robustness of continuation power flow computation[J].Proceedings of the CSEE,2005,25(22):7-11.

[15]Ejebe G C,Tong J,Waight J G,et al.Available transfer capability calculations[J].IEEE Transactions on Power Systems,1998,13(4):1521-1527.

[16]江伟,王成山.电力系统输电能力研究中 PV 曲线的求取[J].电力系统自动化,2001,25(1):9-12.Jiang Wei,Wang Chengshan.PV curves tracing in power system transfer capability analysis[J].Automation of Electric Power Systems,2001,25(1):9-12.

[17]彭志炜,胡国根,韩祯祥.电力系统PV 曲线的追踪与极值分叉点的确定[J].电网技术,1997,21(8):13-16.Peng Zhiwei,Hu Guogen,Han Zhenxiang.Tracing power system PV curve and searching for bifurcation points[J].Power System Technology,1997,21(8):13-16.

[18]Liang Min,Abur A.Total transfer capability computation for multi-area power systems.IEEE Transactions on Power Systems,2006,21(3):1141-1147.

[19]潘雄,徐国禹.基于最优潮流并计及静态电压稳定性约束的区域间可用输电能力计算[J].中国电机工程学报,2004,24(12):86-91.Pan Xiong,Xu Guoyu.OPF based ATC calculation with static voltage stability constraints[J].Proceedings of the CSEE,2004,24(12):86-91.

[20]Mohn F W.Tracing PV and QV curves with the help of a CRIC continuation method[J].IEEE Transactions on Power Systems,2006,21(3):1115-1122.

[21]De Souza ACZ.Discussion on some voltage collapse indices[J].Electric Power Systems Research,2000,53(1):53-58.