模块化光伏并网逆变器的线性功率控制

李威辰 陈桂鹏 崔文峰 李武华 何湘宁

（浙江大学电气工程学院 杭州 310027）

1 引言

近年来，光伏发电并网系统倍受关注并日益普及[1-4]。由于初期投资大，发电成本高，为了缩短成本回收周期，更快地创造经济效益，对光伏并网逆变器的效率以及可靠性提出了更高的要求[5-8]。传统的中大功率光伏发电系统主要有集中式和串式两种结构[9,10]，但都无法实现欧洲效率的优化[11]，并且故障时都会导致电能的大量流失。为了优化系统效率，提高可靠性，模块化光伏发电系统是一种更好的选择[12]。该方案可动态调整运行模块的数量实现功率匹配，实现了宽范围效率提升[13]；还可通过并联冗余来大大提高可靠性。基于以上优点，模块化光伏发电系统近年来倍受青睐，成为一个新的发展趋势。

目前模块化光伏发电系统中，基于CAN 总线的主从控制方案应用广泛[14]。主从控制方案易于实现，均流效果较好。但是主模块和从模块地位不均等，一旦主模块出现故障，整个系统需停机，或者通过控制机制遴选替补主模块。另外，主模块一直处于运行状态，增加了故障概率，影响了系统的整体可靠性。为了提高可靠性，文献[15]对主从控制方案进行改进，提出了层次控制方案，如图1 所示。

图1 层次控制方案Fig.1 Hierarchical control strategy

在系统控制层，中央控制器用来优化系统运行以及控制系统输入电压。由MPPT 算法给定电压参考Vref，与电压采样Vsamp比较得到误差信号并送入电压控制环，最终输出电流参考Iref。在模块控制层，各模块电流指令Irefx（x=1～N，下同）相同，并与各自的电流采样Isampx比较得到误差信号，送入电流控制环，最终输出Ioutx实现单一的并网电流控制。因此所有模块的地位均等，任何一个模块故障均不影响整个系统的运行，而中央控制器仅进行采样与控制运算，没有功率变换环节，因此整个系统的可靠性较高。但是，中央控制器通过CAN 总线将电流指令传送给所有模块，而CAN 总线除了传输控制信息外，还要传输各模块的运行状态以及中央控制器的调度指令等信息，导致电压控制环的控制带宽受到很大限制，影响了系统的动态调节特性。当光伏组件输出功率剧烈变化时，母线电压波动严重。而母线电压过大的波动不仅给系统带来额外的电气冲击，还使得光伏组件的工作点偏离了最大功率点，降低了MPPT 效率。特别在光照减弱时，母线电压下跌还会恶化并网电流质量，影响系统的稳定运行。图2 为光伏组件输出功率下降时的仿真波形。仿真平台与最终实验样机相同，采用传统的控制方案[16]，母线电压指令值为500V，其余参数与实验样机使用的参数相同。仿真中CAN 总线传输电流指令的周期为3ms，当光伏组件输出功率由40kW 降至20kW时，母线电压vbus由500V 跌至426V，下跌幅度超过70V。由于逆变器运行性能受制于母线电压利用率，母线电压跌落使并网电流ia出现畸变，严重时还会触发系统的欠电压保护，使整个系统停机。因此，需要研究行之有效的控制方法来抑制母线电压随光照变化的波动。

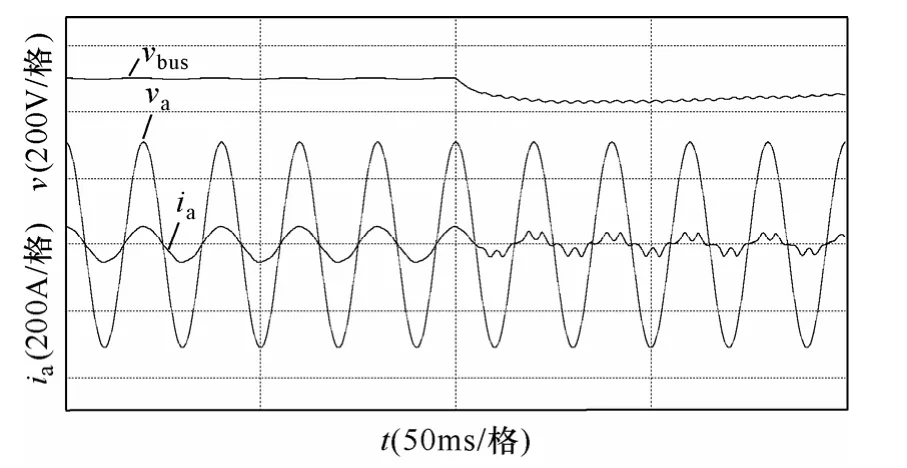
图2 光伏组件输出功率下降仿真波形Fig.2 Simulation waveforms for decrease of PV panel output power

本文采用基于CAN 总线的层次控制架构，提出了“线性功率控制方法”，将母线电压引入模块的并网电流控制指令中，提高了系统的响应速度，使系统能够应对光照强度的快速变化且稳定运行。论文分析了CAN 总线传输速度对系统控制性能的影响，采用提出的线性功率控制方法改变了传统模块的恒功率输出特性，并以三电平逆变器为例通过小信号模型，建立系统控制框图，揭示该方法对系统控制性能的改善机理。最后在40kW 双模块并联系统中，验证了理论分析的正确性和有效性。

2 线性功率控制

通过分析光伏组件和逆变器两者工作时的相互作用关系，可进一步阐明层次控制方案中光伏组件输出功率变化导致母线电压波动的根本原因。图3为光照变化时，光伏组件功率特性曲线的变化趋势。首先，光伏组件的功率特性曲线为PV1。以CAN 总线传送电流指令周期为3ms，开关频率为16kHz 的系统为例，电流控制环带宽一般在1kHz 左右。因此电流控制环的响应速度快于CAN 总线传送电流指令的速度。在下一次传送电流指令之前，所有模块均以前一次接收到的电流指令值控制并网电流。假定电网电压固定不变，并网电流恒定则模块的输出功率不变。因此所有模块共同构成一个恒功率特性的负载，其功率特性曲线为图3 的INV1。最终在MPPT 算法控制下，工作点即PV1与INV1的交点稳定在A 点，对应光伏组件输出电压为VA。

图3 光照变化时光伏组件输出功率特性变化Fig.3 Output power characteristic variation of PV panel under changing illumination

当光照骤然增强，光伏组件的功率特性曲线由PV1变化到PV2。但是由于CAN 总线通信速度的限制，导致模块总功率特性曲线无法快速变化。因此新的工作点为PV2与INV1的交点，即B 点，对应的光伏组件输出电压为VB。由此可得逆变器母线的电压变化为

同理当光照骤然减弱，光伏组件的功率特性曲线由PV1变化到PV3。而PV3与INV1没有交点，此时存在瞬时的功率失配，这将导致如图2 仿真波形所示的母线电压大幅骤降，恶化并网电流质量并降低系统的可靠性。

综上可得，母线电压波动大小与功率特性曲线是否存在交点以及交点位置变化的大小相关。如果控制了交点位置变化范围，即可控制母线电压波动的幅度。如图3 所示，如果模块总功率特性曲线由INV1变化为INV2，则光伏组件的输出功率骤升时，工作点由A 点变化到C 点，对应逆变器母线的电压变化为

从图3 中可以看出

而光伏组件的输出功率骤降时，功率特性曲线存在交点D，对应母线电压下跌幅度得到了控制，为

因此，改变模块的功率特性曲线可以抑制母线电压的波动，而与模块恒功率特性曲线INV1不同，INV2的模块功率特性曲线呈线性，因此本文将使模块功率特性呈现线性的控制方法称为“线性功率控制”。

3 线性功率控制法的实现

为了陈述线性功率控制法的具体实现方式以及关键参数的选取，设计了模块化光伏发电系统，如图4 所示，其中电路参数以及控制参数与实验样机的参数相同。该系统包括两个相同的模块。模块采用LCL 滤波的T 形三电平拓扑。图4b 中，电感L1电流ia1、ib1和ic1用于做并网电流控制，电感L2电流ia2、ib2和ic2三者之和通过PI 控制用于抑制并联模块之间的环流[12]。

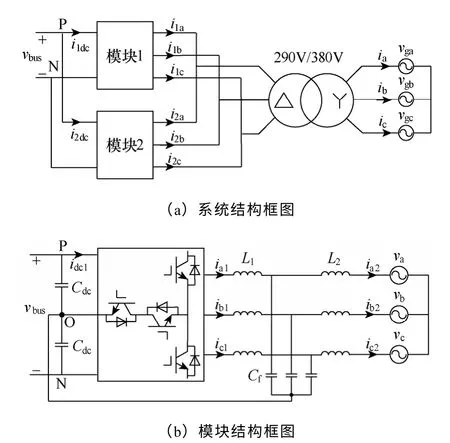
图4 模块化光伏发电系统Fig.4 Modular PV generation system

线性功率控制方案如图5 所示，中央控制器将电压控制环的参考vbusref和输出idref通过CAN 总线传给模块。模块根据母线电压vbus通过式（5）得出d 轴（有功）电流指令值id1ref。

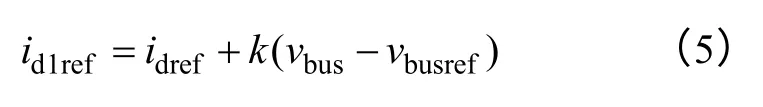
式中，k为线性功率控制的线性斜率。

由式（5）可得，并网电流与母线电压呈线性关系，而电网电压固定不变，模块的输出功率与母线电压也呈线性关系。因此模块呈现图3 中INV2的功率特性曲线。当k=0 时，线性功率控制退化成传统恒功率特性模块控制。稳态下，母线电压vbus与vbusref相等，电压控制环输出仍为电流控制环的指令值。而动态下vbus偏离vbusref，在idref不变时，id1ref仍可以快速变化做出响应，缩短了系统的动态响应时间。线性功率控制中，模块伏安特性呈线性，k表征了母线电压变化时并网电流变化的幅度，为模块的“等效虚拟电导”。

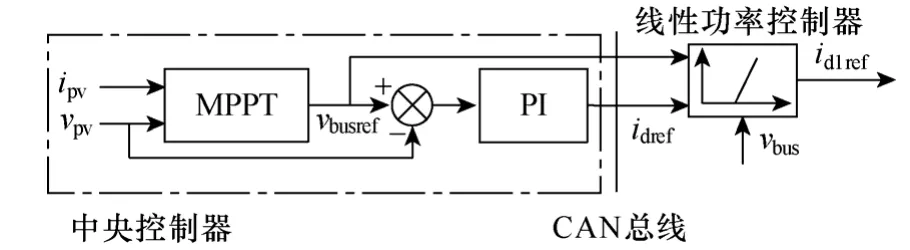
图5 线性功率控制方案Fig.5 Linear power control strategy

4 线性功率控制关键参数设计

在线性功率控制中，式（5）中线性斜率k的大小会影响系统的控制性能。通过三电平并网逆变器小信号模型，得到系统控制框图以及传递函数，从而揭示参数k的大小对系统控制性能的影响。

4.1 电流控制环传递函数

忽略dq 轴之间的耦合关系，在d 轴可得占空比到L1电感电流的传递函数为[16,17]

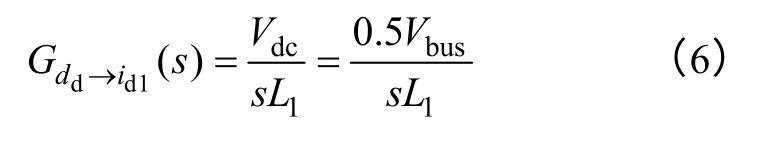
模块电流控制环的控制框图如图6 所示。其他各环节的表达式如式（7）～式（10）所示。

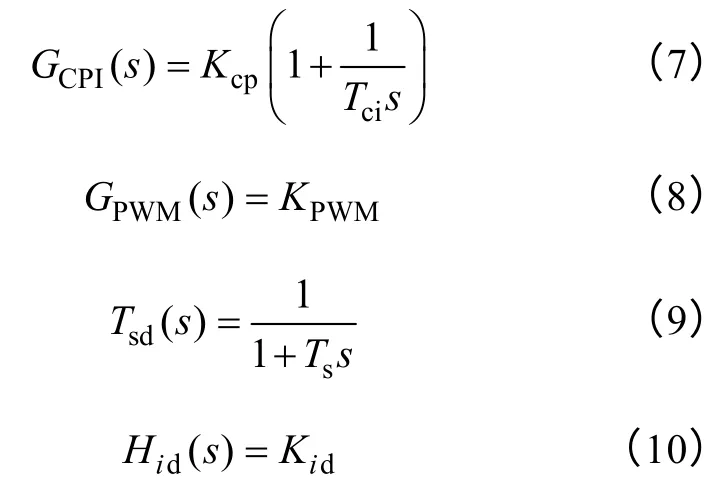
式中，GCPI为电流环PI 调节器；GPWM为PWM 调制环节；Tsd为等效采样延迟环节，由于每个开关周期采样一次，延迟时间等于开关周期Ts；Hid为电流采样环节。

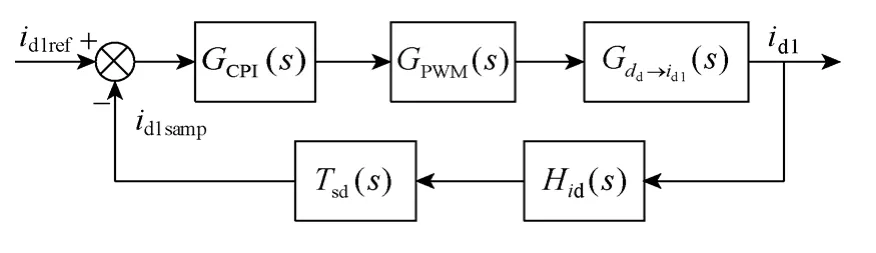
图6 电流控制环框图Fig.6 Block diagram of current control loop

最终可得电流控制环的开环和闭环传递函数表达式分别为

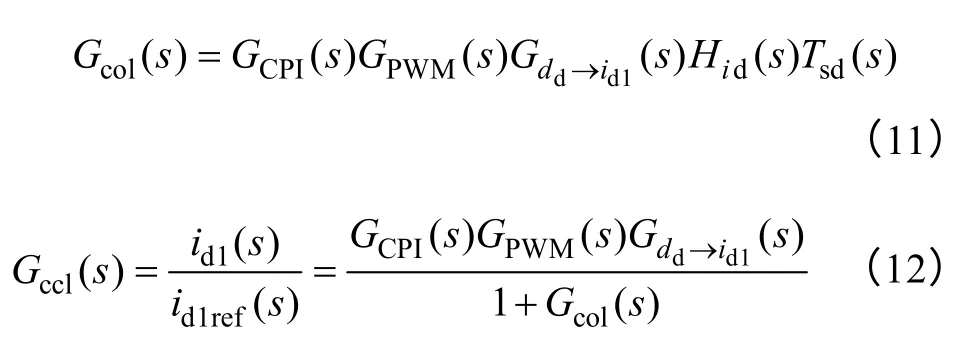
综上所述，图6 所示的电流控制环可等效成由电流指令值到实际电流输出的单一控制环节，该环节的传递函数即闭环传递函数Gccl，并在此基础上进一步建立系统控制框图。

4.2 线性功率控制器的设计

图7 为LCL 滤波三电平并网逆变器直流侧的小信号模型[16,17]。为了简化分析，假设三相完全对称，忽略O 轴分量。图中带“^”符号为在稳态工作点附近的小信号扰动量。Id1和Iq1分别为L1电感电流稳态工作点的d 轴和q 轴分量，分别为对应的小信号扰动量；分别为d 轴和q 轴占空比的小信号扰动量；Ddp和Dqp分别为逆变器桥臂上管占空比稳态工作点的d 轴和q 轴分量；Ddn和Dqn分别为逆变器桥臂下管占空比稳态工作点的d 轴和q 轴分量。

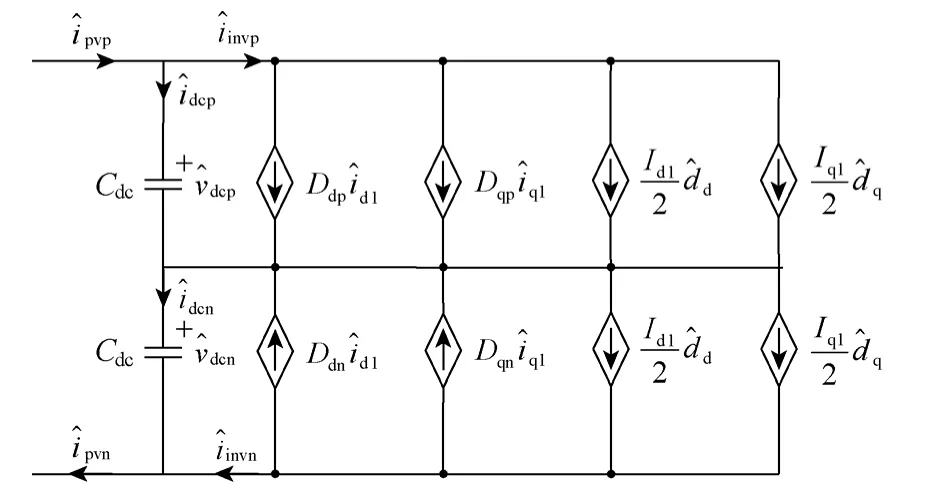
图7 LCL 滤波三电平并网逆变器的直流侧小信号模型Fig.7 DC side small signal model of three level grid-connected inverter with LCL filter

为了考察d 轴电流id1对母线电压的影响，忽略其他扰动项，根据图7 可得

考虑到n个模块并联后，正负母线的电容Cdc以及正负母线上桥臂电流都扩大到原来的n倍，因此流过正负母线电容的电流为

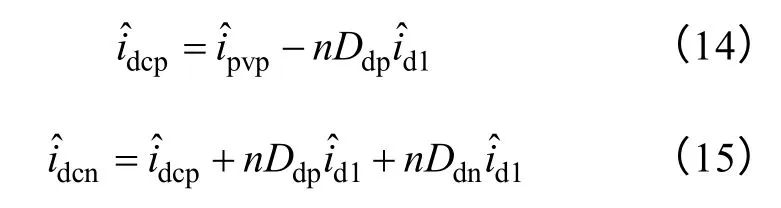
则母线电压为

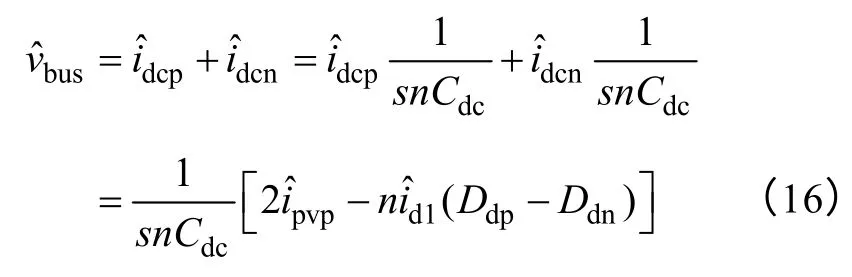
若采用SPWM 调制，则

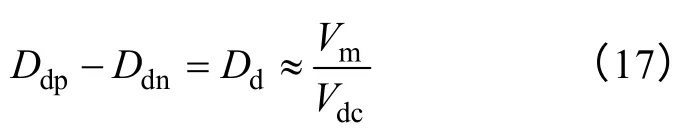
式中，Vm为交流相电压峰值；Vdc为正负母线电容Cdc电压。由此得出d 轴电流id1与母线电压的关系表达式为

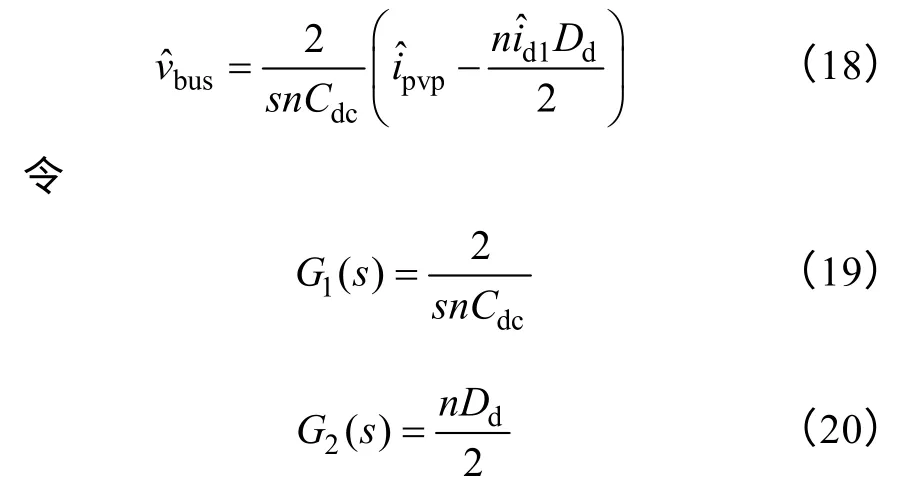
如图5 所示中央控制器将电压环参考值vbusref和电压环输出值idref周期的通过CAN 总线传送给各个模块。考虑到MPPT 周期较长，扰动步长较小，因此电压环参考值vbusref变化较小，受CAN 总线通信的影响较小。为方便分析，设定电压环参考值vbusref恒定不变。最终引入电压环后系统控制框图如图8 所示，控制环节表达式如式（19）～式（23）所示。

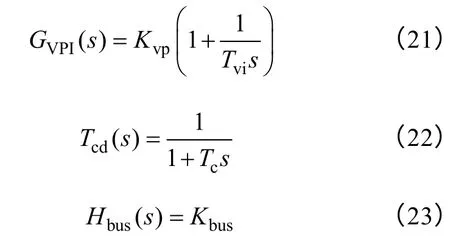
式中，GVPI(s) 为电压环PI 调节器；Tcd(s) 为等效通信延时环节；Hbus(s) 为母线电压采样环节。

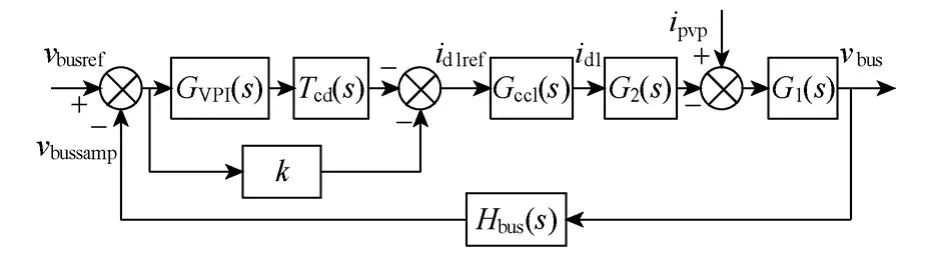
图8 系统控制框图Fig.8 Control block diagram of system

传统控制方案中k=0，根据图8 可得补偿前系统开环传递函数Gsysol1(s) 为

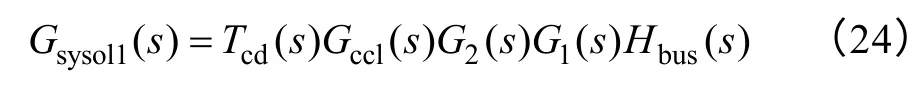
当通信延时Tc取不同值时，绘制Gsysol1(s) 伯德图如图9 所示。从图中可以看出，通信延时会导致相位滞后，延时越大则滞后越严重。因此为了有足够的相位裕量，穿越频率要向低频偏移，使得系统控制环带宽偏低，动态特性变差。因此，传统控制方案中通信速度对系统的控制性能有较大的影响。

图9 不同Tc时Gsysol1(s) 伯德图Fig.9 Bode diagram of Gsysol1(s) with different Tc

采用线性功率控制后，在系统控制框图上相当于在原有电压控制环基础上引入一个比例环节。当母线电压发生变化时，误差信号可以直接调节电流指令值，不再受通信的影响，提高了系统的响应速度。根据图8 可得补偿后系统开环传递函数为

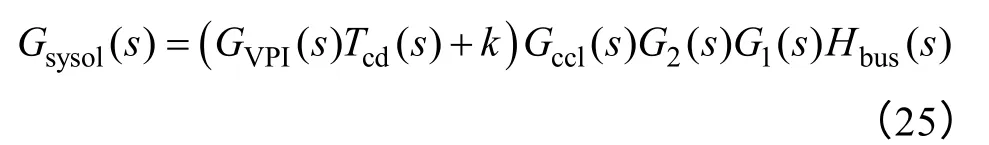
当Tc=0.003s，k取不同值时，系统开环传递函数伯德图如图10 所示。当k=0 时，退化为传统的恒功率特性模块控制。从图中可以看出，当k值增大时，穿越频率提高，相位裕量增加，系统的控制性能得到了改善。

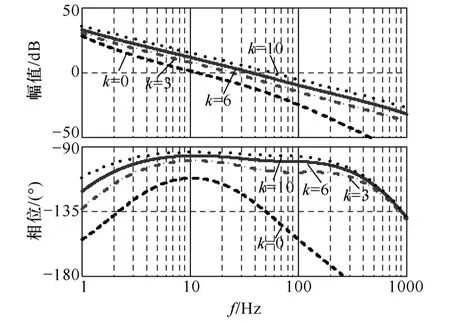
图10 不同k 值时系统开环传递函数伯德图Fig.10 Bode diagram of system open-loop transfer function with different k

为了考察前面所提到的光伏组件输出功率变化对母线电压产生的影响。根据图8 可得光伏组件输出电流ipvp到母线电压vbus的闭环传递函数为

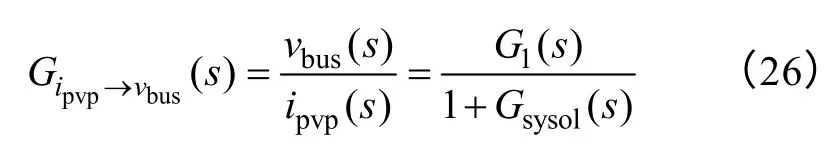
以线性斜率k为参数，根据式（26）绘制系统参数根轨迹图如图11 所示。该系统为典型的高阶系统，可根据闭环主导零极点对其进行分析。式（26）的闭环零点中除原点之外，其余均远离虚轴；从图11b 可知，系统仅有一个闭环主导极点，随着k增大向虚轴靠近，导致系统阻尼增大，调节时间增加。因此k值的选取受调节时间所限。在实际应用中，调节时间选取MPPT 扰动周期的一半为宜。由于系统MPPT 扰动周期为2s，因此调节时间选取1s 左右。采用闭环主导零极点估算系统调节时间，其阶跃响应为指数衰减过程，取调节时间为时间常数T（T为主导极点的倒数）的4 倍，对应计算出k为5.54。实际应用中k取整数值6，对应主导极点为-3.78，调节时间为1.06s，满足设计要求。

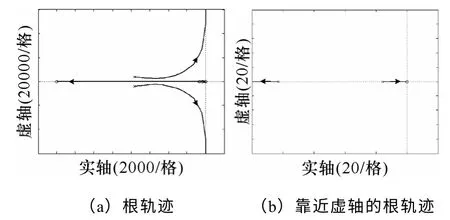
图11 系统根轨迹图Fig.11 Root locus of system

当光照变化时，光伏组件伏安特性曲线发生变化，但变化最大的是短路电流，而开路电压变化很小。此外，光伏组件在最大功率点左侧呈现恒流特性。即使光伏组件的输出电压下跌很多，输出电流也变化很小。因此当光照由强变弱导致输出功率骤降时，可以简单等效成一个恒流源输出电流的变化。

设定光照下降导致光伏组件输出功率由40kW降至20kW，最大功率点电压不变，均为600V，则等效恒流源输出电流变化为33A。由此可得母线电压的阶跃响应为

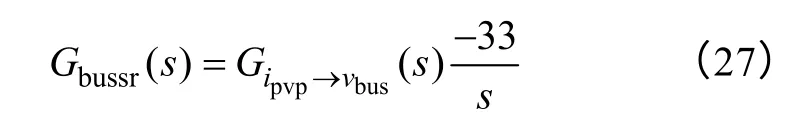
将式（27）进行拉普拉斯反变换，得到时域的表达式并绘制阶跃响应曲线如图12 所示。从图12中可以看出，采用线性功率控制，当系统输入功率变化时，电压下跌幅度明显减小。k值越大，电压波动越小，但是调节时间也越长，与前面理论分析一致。

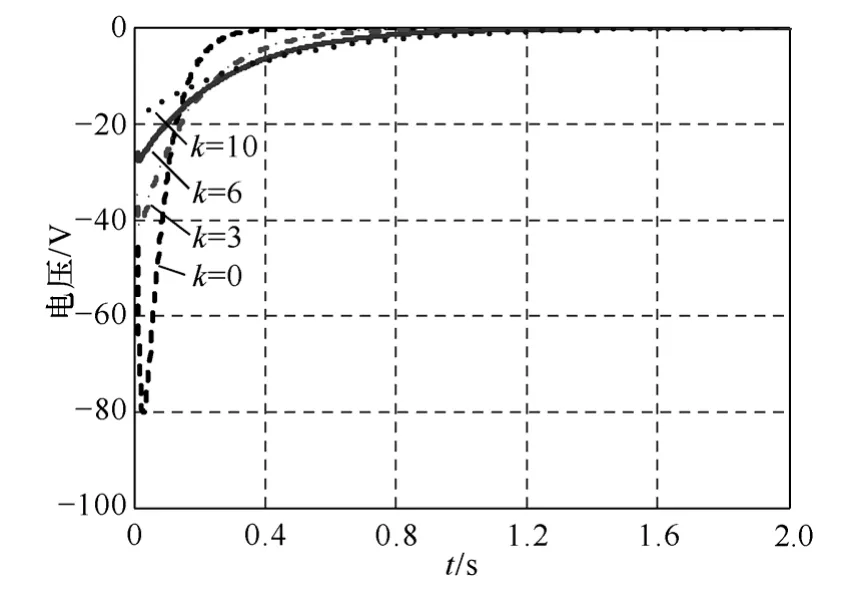
图12 不同k 值下系统阶跃响应曲线Fig.12 Step response curves of system with different k

5 实验分析

为了验证线性功率控制的有效性，根据图4 搭建实验样机，样机参数见下表。实验采用两台型号为TC.P.32.1000.400.PV.HMI 的REGATRON 光伏模拟器并联模拟光伏组件，并预设最大功率分别为20kW和40kW，对应电压均为600V 的两条光伏特性曲线，对系统进行稳态和动态下的测试。

表 实验样机参数Tab.Parameters of prototype

图13 为系统满载运行时，电网A 相电压vga，并网A 相电流ia，模块1和模块2 输出A 相电流i1a、i2a波形。从图13 中可以看出，系统稳态运行良好，并网电压与并网电流同频同相，功率因数接近1。模块1 与模块2 输出电流幅值相同，均流效果良好。

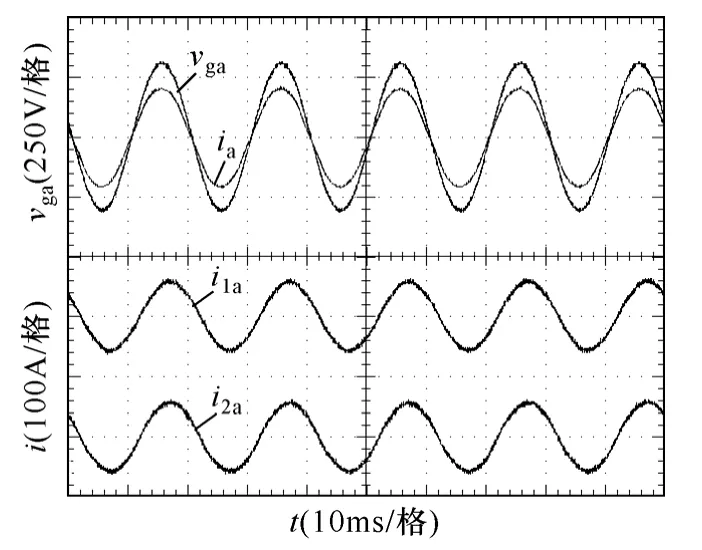
图13 系统稳态波形Fig.13 Steady-state waveforms of system

图14 为采用传统控制方案和线性功率控制方案，在系统由满载降为半载时，母线电压vbus，并网电流ia，模块1和2 的输出电流i1a、i2a的波形。采用传统控制方案，当输入功率变化时，母线电压下跌了75V；而采用线性功率控制，母线电压仅下跌25V。通过对比可得采用线性功率控制，母线电压的波动明显减小。因此，线性功率控制对输入功率变化导致的母线电压波动有良好的抑制效果。

图14 系统动态波形对比Fig.14 Dynamic waveforms comparison of system

图15 为半载和满载下，光伏模拟器模拟的光伏特性曲线和系统实时工作点。MPPT 由中央控制器的MPPT 控制环实现。实验结果显示，采用线性功率控制，功率变化前后，系统均工作在最大功率点，MPPT 性能良好。

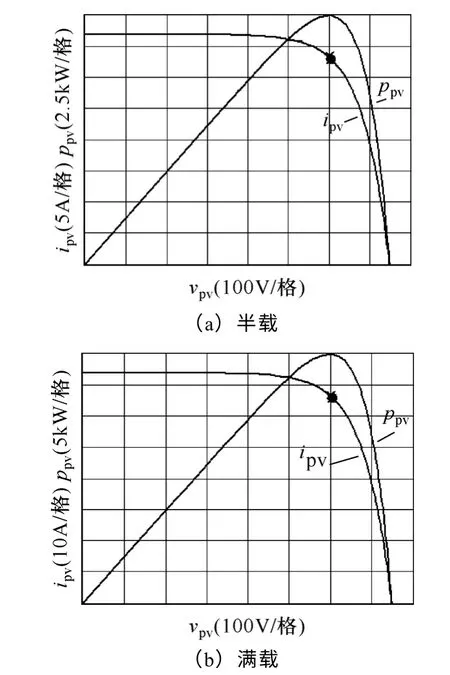
图15 系统MPPT 性能Fig.15 MPPT performance of system

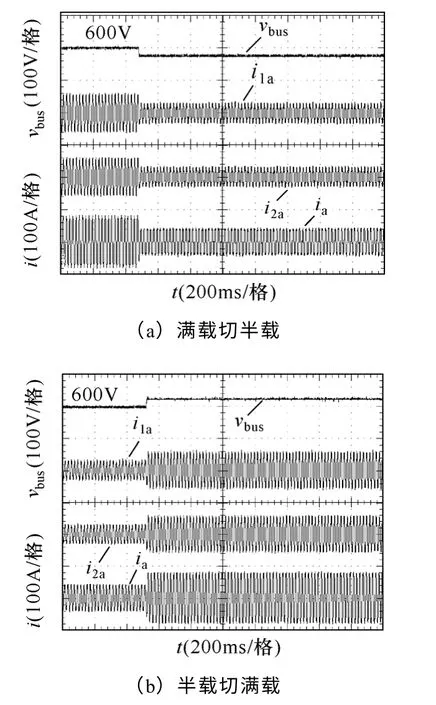
图16 通信中断时系统动态波形Fig.16 Dynamic waveforms of system under communication interrupt

图16 为通信线断开，系统输入功率变化时实验波形。当通信线断开后，各个模块无法接收到中央控制器发送的控制信息，中央控制器的母线电压控制环失效。根据图3 所示，采用线性功率控制，无论功率升高还是下降，光伏组件与模块功率特性曲线均存在交点，并且交点位置变化的范围受到了限制，因此母线电压的变化幅度也受到限制。从图16 可以看出，在通信线故障断开，系统输入功率变化的情况下，并网电流仍可根据功率变化而快速变化。母线电压的波动被限制在一定的小范围内，系统仍可维持运行，增加了系统可靠性，与理论分析一致。

综上所述，和传统的恒功率特性模块控制相比，采用线性功率控制法，系统依然保持良好的稳态性能，提高了动态响应速度，抑制了光照变化导致系统输入功率变化时母线电压的波动，使系统稳定的运行。此外即使在通信中断的情况下，在输入功率变化时系统仍可以控制母线电压在一个小范围变化，提高了系统的可靠性。

6 结论

本文基于采用CAN 总线层次控制的模块化光伏发电系统，提出了线性功率控制方法，提高了系统的响应速度，使系统在光照强度剧烈变化时更稳定的运行。通过分析传统控制中CAN 总线传输速度对系统控制性能的影响，引入线性功率控制，改变了传统模块恒功率的特性，缩短了系统的响应时间，抑制了光伏组件输出功率变化导致的母线电压波动。文中以LCL 滤波T 形三电平电路作为模块拓扑，搭建了双模块并联的模块化光伏发电系统。通过小信号模型，建立系统控制框图，得出采用线性功率控制可以提高系统的穿越频率，增加系统的相位裕量，并分析了线性功率控制中功率特性曲线的斜率大小对系统控制性能的影响，斜率越大，光照变化时母线电压波动越小，但调整时间越长。最后，通过实验验证了理论的分析结论。

[1]刘方锐,段善旭,康勇,等.多机光伏并网逆变器的孤岛检测技术[J].电工技术学报,2010,25(1):167-171.Liu Fangrui,Duan Shanxu,Kang yong,et al.Islanding detection methods for multiple PV converters system[J].Transactions of China Electrotechnical Society,2010,25(1):167-171.

[2]陈昌松,段善旭,殷进军.基于神经网络的光伏阵列发电预测模型的设计[J].电工技术学报,2009,24(9):153-158.Chen Changsong,Duan Shanxu,Yin Jinjun.Design of photovoltaic array power forecasting model based on neutral network[J].Transactions of China Electrotechnical Society,2009,24(9):153-158.

[3]李冬辉,王鹤雄,朱晓丹,等.光伏并网发电系统几个关键问题的研究[J].电力系统保护与控制,2010,38(21):208-214.Li Donghui,Wang Hexiong,Zhu Xiaodan,et al.Research on several critical problems of photovoltaic grid-connected generation system[J].Power System Protection and Control,2010,38(21):208-214.

[4]朱克平,江道灼.一种改进型的光伏并网逆变器[J].电力系统保护与控制,2013,41(6):99-104.Zhu Keping,Jiang Daozhuo.An improved inverter for a grid-connected photovoltaic power system[J].Power System Protection and Control,2013,41(6):99-104.

[5]刘邦银,段善旭,刘飞,等.基于扰动观察法的光伏阵列最大功率点跟踪[J].电工技术学报,2009,24(6):91-94.Liu Bangyin,Duan Shanxu,Liu Fei,et al.Photovoltaic array maximum power point tracking based on improved perturbation and observation method[J].Transactions of China Electrotechnical Society,2009,24(6):91-94.

[6]杨水涛,张帆,丁新平,等.基于输入-输出参数的光伏电池最大功率控制的比较[J].电工技术学报,2009,24(6):95-102.Yang Shuitao,Zhang Fan,Ding Xinping,et al.Comprehensive research on the photovoltaic maximum power point tracking based on input parameters or output parameters[J].Transactions of China Electrotechnical Society,2009,24(6):95-102.

[7]高志强,王建赜,纪延超,等.一种快速的光伏最大功率点跟踪方法[J].电力系统保护与控制,2012,40(8):105-109.Gao Zhiqiang,Wang Jianze,Ji Yanchao,et al.A fast method of maximum power point tracking for PV[J].Power System Protection and Control,2012,40(8):105-109.

[8]高金辉,唐静.一种新型光伏系统最大功率算法的研究[J].电力系统保护与控制,2011,39(23):21-29.Gao Jinhui,Tang Jing.A novel MPPT method foer PV systems[J].Power System Protection and Control,2011,39(23):21-29.

[9]Wu L,Zhao Z,Liu J.A Single-stage three-phase grid-connected photovoltaic system with modified MPPT method and reactive power compensation[J].IEEE Transactions on Energy Conversion,2007,22(4):881-886.

[10]Agorreta J L,Borrega M,Lopez J,et al.Modeling and control of n-paralleled grid-connected inverters with LCL filter coupled due to grid impedance in PV plants[J].IEEE Transactions on Power Electronics,2011,26(3):770-785.

[11]Araujo S V,Zacharias P,Mallwitz R.Highly efficient single-phase transformerless inverters for gridconnected photovoltaic system[J].IEEE Transactions on Industrial Electronics,2010,57(9):3118-3128.

[12]张兴,邵章平,王付胜,等.三相三电平模块化光伏并网系统的零序环流抑制[J].中国电机工程学报,2013,33(9):17-24.Zhang Xing,Shao Zhangping,Wang Fusheng,et al.Zero-sequence circulating current reduction for threephase three-level modular photovoltaic grid-connected systems[J].Proceedings of the CSEE,2013,33(9):17-24.

[13]张犁,胡海兵,冯兰兰,等.模块化光伏并网系统欧洲效率优化控制方法[J].中国电机工程学报,2012,32(9):7-13.Zhang Li,Hu Haibing,Feng Lanlan,et al.European efficiency improvement control for grid-connected modular photovoltaic generation systems[J].Proceedings of the CSEE,2012,32(9):7-13.

[14]汪海宁.光伏并网功率调节系统及其控制的研究[D].合肥:合肥工业大学,2005.

[15]Borrega M,Marroyo L,Gonzalez R,et al.Modeling and control of a master-slave PV inverter with nparallel inverters and three-phase three-limb inductors[J].IEEE Transactions on Power Electronics,2013,28(6):2842-2855.

[16]Figueres E,Garcera G,Sandia J,et al.Sensitivity study of the dynamics of three-phase photovoltaic inverters with an LCL grid filter[J].IEEE Transactions on Industrial Electronics,2009,56(3):706-717.

[17]李霄.质子交换膜燃料电池功率变换系统控制研究[D].杭州:浙江大学,2012.