级联系统中Buck 充电调节器前馈控制方法

贾鹏宇 郑琼林 李 艳 王蓓蓓

（北京交通大学电气工程学院 北京 100044）

1 引言

电源控制器（Power Conditioning Unit,PCU）是航天器一次电源系统中的核心构成部分，广泛应用于卫星、空间站和探测器等航天器产品中。现阶段大部分PCU 产品采用的是太阳电池阵/蓄电池的电源系统结构，其功能是实现将太阳能进行光伏转换为蓄电池充电，为母线负载提供电能，并在光照不足或者负载较重时使蓄电池放电保证母线负载正常工作。通常按照PCU 的母线电压变化范围可分为三类：不调节、半调节以及全调节母线系统。近年来卫星上广泛使用的PCU 系统多采用后两种调节母线方式[1,2]，一般由分流调节器（Shunt Regulator,SR）、蓄电池充电调节器（Battery Charge Regulator,BCR）和蓄电池放电调节器（Battery Discharge Regulator,BDR）三部分构成[2-6]，其对外接口一般包括：太阳电池板、蓄电池、母线负载以及上位机通信接口。

图1 为全调节母线型PCU 系统架构图，其中SA 表示太阳电池板阵列。当PCU 运行在光照区轻载工况时，太阳电池板输出电流ISA较为充足，SR进行分流调节[2-7]，将部分电流IS回流至电池板，以维持母线恒定，此时BCR 模块输入从母线取电，为蓄电池进行充电；当PCU 系统运行在阴影区重载工况时，蓄电池通过BDR 放电以维持母线电压恒定。SR 部分硬件常采用顺序开关分流调节器（Sequential Switching Shunt Regulator，S3R）实现，图2 为其基本原理图，根据功率等级和太阳电池板数量决定其级数n。由于SR 模块多采用滞环控制[7-10]，导致母线上存在一定频率的纹波，这就使得BCR 的输入电压中存在电压扰动，从而使蓄电池电压和充电电流含有同频率的脉动，使得BCR 引入噪声，损耗和器件应力增大，影响PCU 系统的稳定性。因此控制衰减BCR 模块前向通道的闭环输入电压-输出电压传递函数A(s)，即音频敏感率（audio susceptibility），是BCR 设计的重要内容。

文献[11]指出了带有输入滤波器的Buck 型变换器在采用前馈控制时可以消除输入滤波器的输出阻抗对Buck 变换器控制环路的影响，并给出了加入前馈控制后音频敏感率A(s)衰减的效果，但没有对此进行深入分析；文献[12]推导了变换器的一般状态空间方程，并且选定比例控制器对基本的电路拓扑进行前馈控制，得到了在调整音频敏感率A(s)为零时，前馈比例系数需要满足的条件。但当变换器的模型阶次较高时，单独采用比例控制器无法实现全频率范围内音频敏感率的调零，因此需要对前馈控制器的精确形式进行探讨；文献[13,14]基于Buck和Boost 等基本变换器给出了一种变三角波幅值的载波实现电路，能够实现调整音频敏感率A(s)=0，但载波幅值变化容易增加反馈控制电路的设计难度，降低电源系统的可靠性。

本文首先分析了引入输入电压前馈的 DC-DC变换器的控制框图，给出了闭环控制的变换器中音频敏感率A(s)调整为零的一般条件。接着以航天飞行器中降压类BCR 电源拓扑中常用的Buck 电路为例，通过分析其模型表达式，给出一种简单的能够根据输出侧电压变化而自适应改变前馈控制电路增益的控制实现方法。最后通过搭建S3R 与BCR 构成的级联系统实验平台，模拟了PCU 系统中S3R调节母线电压时由于滞环控制引起的母线电压纹波现象。通过比较不同稳定点工况的Buck 电路在加入前馈控制器前后的输出电压的扰动分量，进行对前馈控制电路设计的验证。

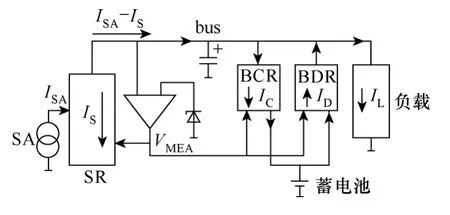
图1 PCU 系统示意图Fig.1 PCU system scheme

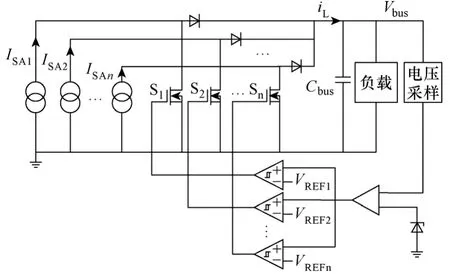
图2 S3R 基本原理图Fig.2 Scheme of S3R

2 引入前馈控制的DC-DC 变换器

图3 表示引入输入电压前馈控制的变换器的一般控制框图。图中Gvg表示开环输入电压-输出电压传递函数，Gvd表示开环占空比-输出电压传递函数，G1表示反馈系统中采用的控制器，G2表示前馈控制器，H表示电压采样系数，Vm表示三角波的幅值，表示输入电压扰动，表示输出电压扰动，表示输出电压指令值扰动，由于一般为直流量给定值，因此为零。

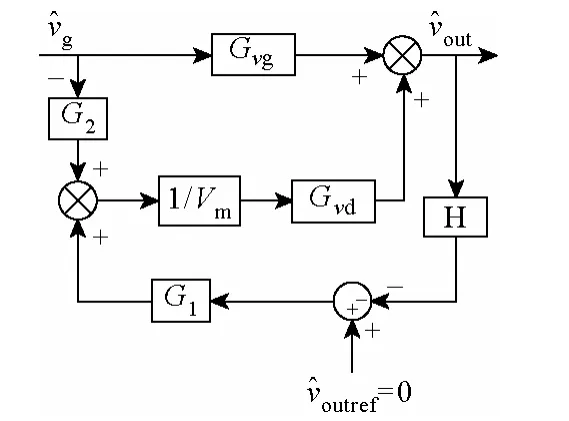
图3 引入输入电压前馈的DC-DC 变换器控制框图Fig.3 Control block diagram of DC-DC converter with feedforward of input voltage

根据图3 所示控制框图，假设采用前馈控制器G2，则可计算得闭环DC-DC 变换器中音频敏感率A(s)的表达式，即

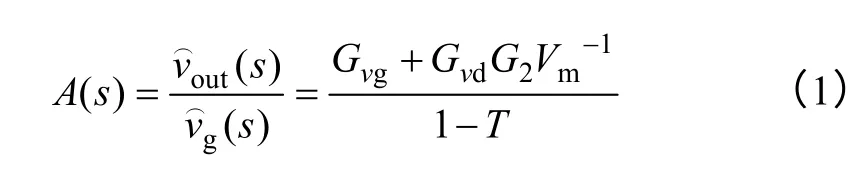
其中，T表示反馈环路增益

可见，若使得等式（1）在全频率范围内为零，则前馈控制器需要满足

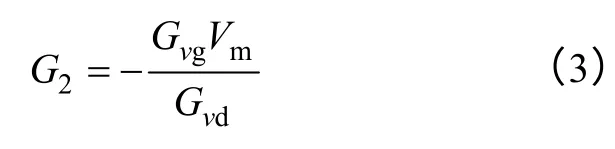
综上所述，当DC-DC 变换器的输入电压前馈控制器满足式（3），则对于任意闭环系统的DC-DC变换器，都会使得其音频敏感率调整为零，实现输出电压对输入电压扰动的解耦。

3 输入电压前馈的Buck 变换器

由于Buck 电路拓扑具有高效，电路结构简单，功率密度大等优点，且其输入滤波器可与主电路分开设计，因此广泛应用于PCU 系统中的降压型BCR拓扑中[15-17]。

以无输入滤波器的Buck 变换器为例，其开环占空比-输出电压传递函数和开环输入电压-输出电压传递函数为

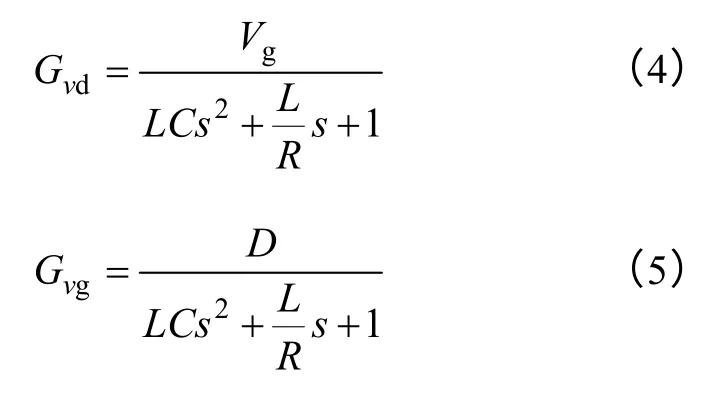
式中，D表示稳态占空比。由此可得，当Buck 电路的前馈控制器G2为

可以实现音频敏感率A(s)=0。

一般为了使Buck 变换器输入电流连续，减小EMI，需要加入LC 阻尼滤波器，如图4 所示。考虑加入LC 阻尼滤波器之后的Buck 电路模型，根据MiddleBrook 阻抗比判据[18]，若滤波器设计的输出阻抗Zout在全频率范围内小于变换器的开环输入阻抗Zin，则可保证LC 滤波器设计的输出阻抗小于Buck 变换器的闭环输入阻抗，并且使得Buck 变换器开环占空比-输出电压传递函数Gvd在加入LC 滤波器前后不受影响。由此可得加入LC 滤波器后，Buck 变换器开环输入电压-输出电压传递函数Gvgo表示为

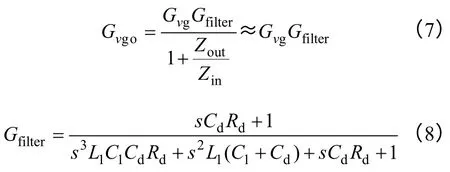
式中，Gfilter表示输入滤波器前向通道传递函数。

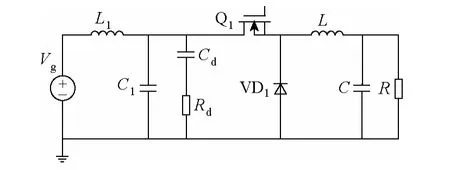
图4 带有输入滤波器的Buck 变换器Fig.4 Buck converter with input filter

综上所述，当输入滤波器参数满足与后级Buck电路输入输出阻抗解耦的条件时，若使得音频敏感率A(s)=0，则前馈控制器需要满足

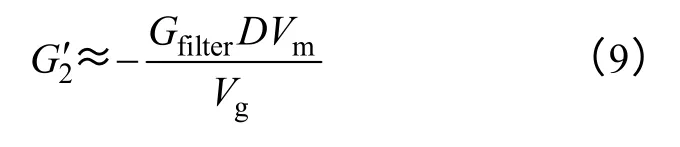
当输入滤波器的输出阻抗Zout与Buck 电路输入阻抗Zin有交截时，则式（7）不再成立，得到的前馈控制器形式将更加复杂。

4 自适应前馈控制器

通过分析可知，式（9）中含有与频率相关的量，无法采用纯比例控制器实现，这在大规模采用高可靠性模拟电路进行控制的PCU 系统中是难以实现的。但是，如果从分离输入滤波器和Buck 电路的角度观察，可以将输入滤波器的电容视为新的母线，则可采用式（6）的比例前馈控制器，实现调整音频敏感率A(s)=0。

式（3）是建立在稳态工作点固定的情况下推导的，即所得到的前馈控制器形式仅针对稳态工作点有效。在PCU 系统中，由于BCR 输出部分连接蓄电池负载，其输出电压随着充电过程的进行而发生变化，因此，固定增益的比例控制器不适用于前馈控制。为此需要改变控制器的实现方法以能够针对不同输出电压自适应调整前馈控制器参数。

以Buck 电路输入滤波器中电容电压vC1作为前馈变量进行控制，则前馈控制器应满足式（6）。当变换器处于稳定工作点时，由于稳态占空比定义为

将式（10）代入式（6），得到

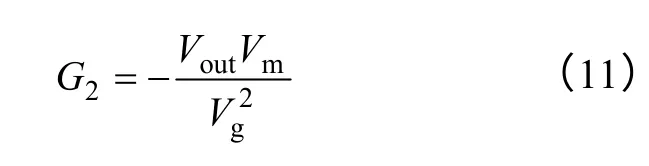
式中，VC1=Vg。

由式（11）可知，前馈控制器的增益与输出电压成正比，与输入电压的平方成反比。换言之，当BCR 输出电压发生变化时，只要Buck 电路的前馈控制器同比例变化，则可保证音频敏感率A(s)为零，比例系数为。由此可得Buck 变换器在作为BCR 时的控制原理图如图5 所示。

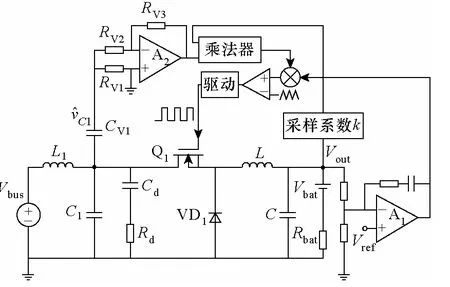
图5 Buck 电路自适应前馈控制环路原理Fig.5 Adaptive feedforward control scheme for Buck circuit

前馈控制电路利用隔直电容CV1以及电阻RV1对输入滤波器电容C1上的电压扰动交流信号进行采样，通过反相比例放大器（增益比为RV3/RV2）给定至乘法器的输入端。通过固定的采样系数k对输出电压进行采样，得到的结果给定至乘法器的输入端，乘法器输出叠加至闭环反馈产生的调制波中，与三角波进行交截，产生脉冲信号控制Buck 电路的开关管。由上述可知，需满足

5 仿真及实验验证

在Buck 电路滤波器的输入电压中加入不同频率扰动量，通过针对不同输出电压和不同功率等级工况进行仿真实验，测试其音频敏感率A(s)。仿真参数见下表，电路采用电压闭环恒压控制，控制器采用比例积分控制器。得到A(s)测试结果如图6 所示。通过仿真结果可知，前馈控制器增加了输出电压对输入电压的抗扰动性，使A(s)≈0。需要说明的是，调整A(s)=0 意味着仿真得到的理论值在对数坐标系中表现为负无穷，但是实际仿真结果会给定一个有限值，其大小与扰动源大小、前馈控制器精度、元器件模型以及步长有关。

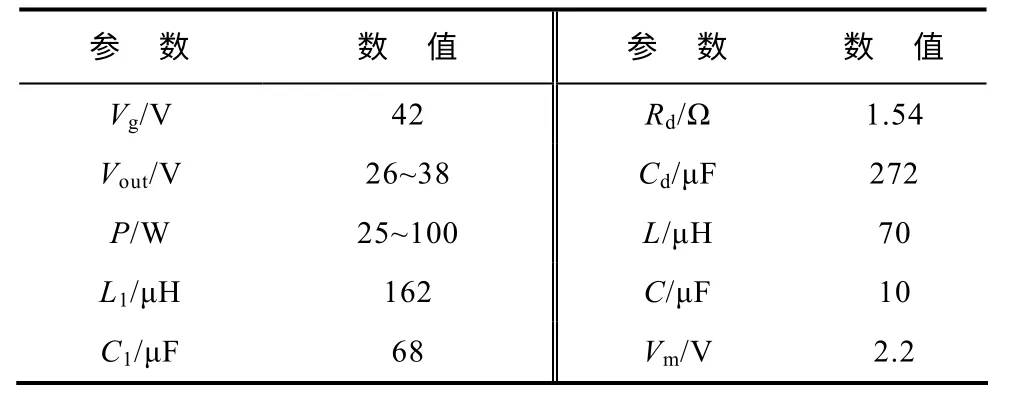
表 仿真参数Tab. Simulation Parameters

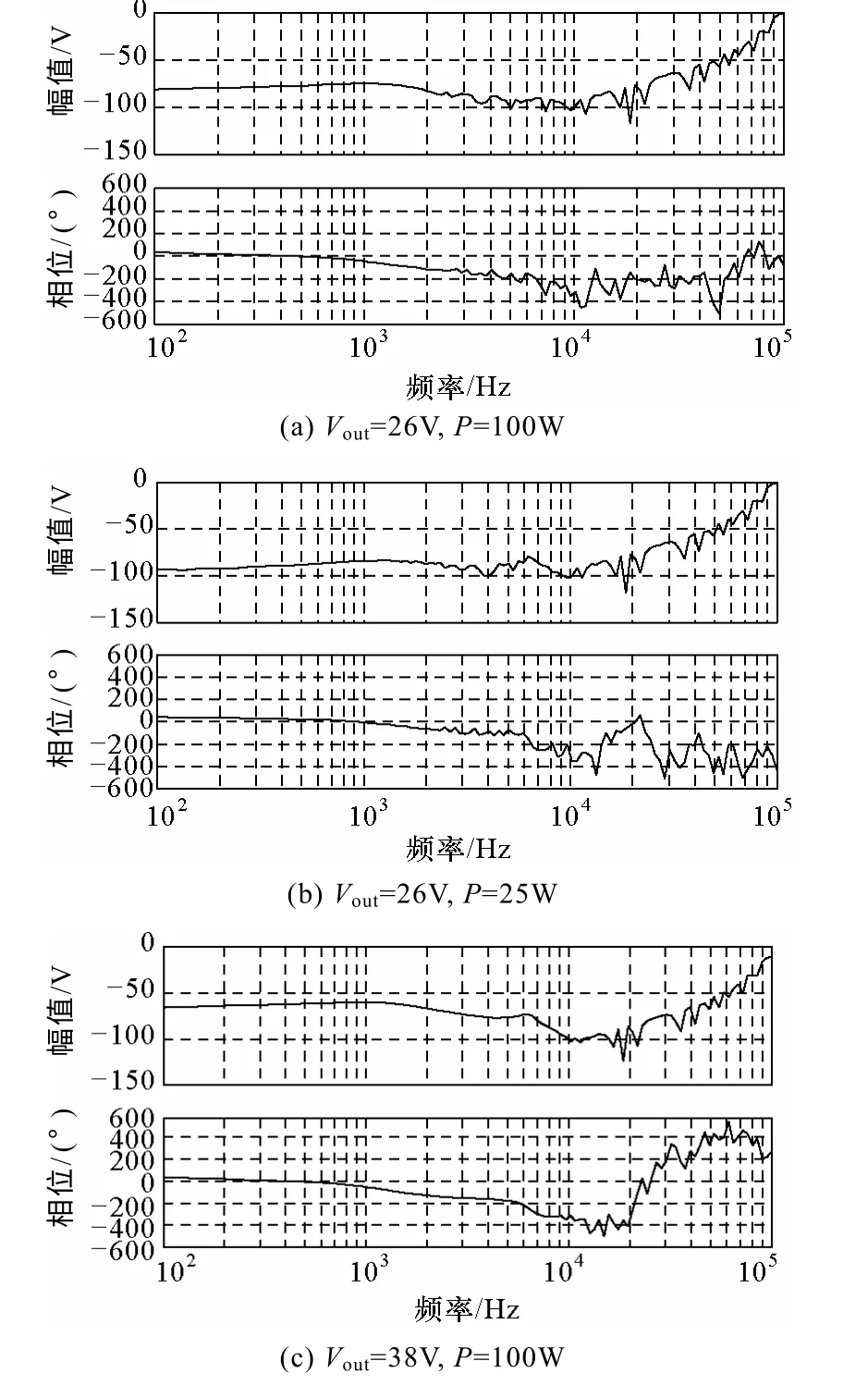
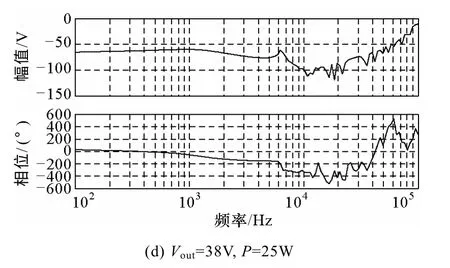
图6 前馈控制下变换器的音频敏感率测试Fig.6 Audio-susceptibility test of converter under feedforward control

搭建系统级联实验平台如图7 所示，以验证前馈控制电路的有效性。实验平台包含一级S3R和Buck 电路构成的BCR，主电路参数见表。其中S3R部分稳定直流母线，采用比例积分得到母线电压误差信号进行滞环控制，因此其纹波频率不固定，随母线负载发生变化，S3R 关键点波形如图8 所示。电流源ISA设定3.5A，母线电压由S3R 稳定在42V，母线电容阵Cbus选择4mF。Buck 电路采用电压环恒压控制，输出电压范围为26～38V。分别对不同稳定工作点的Buck 电路在加入前馈控制前后的输出电压波形进行测试，得到实验结果如图9和图10 所示。

图7 级联系统实验台示意图Fig.7 Cascade system scheme

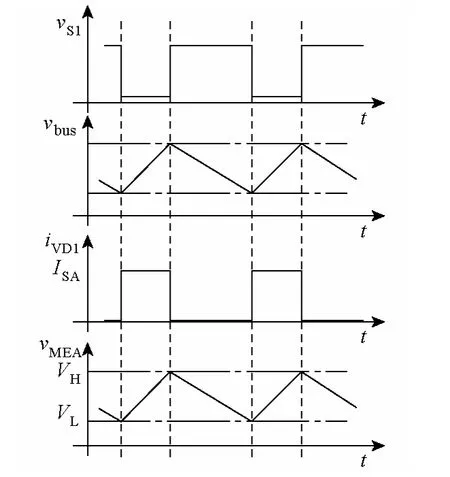
图8 S3R 部分关键点波形Fig.8 Key waveforms of S3R part

图9 无前馈实验波形Fig.9 Waveforms without feedforward

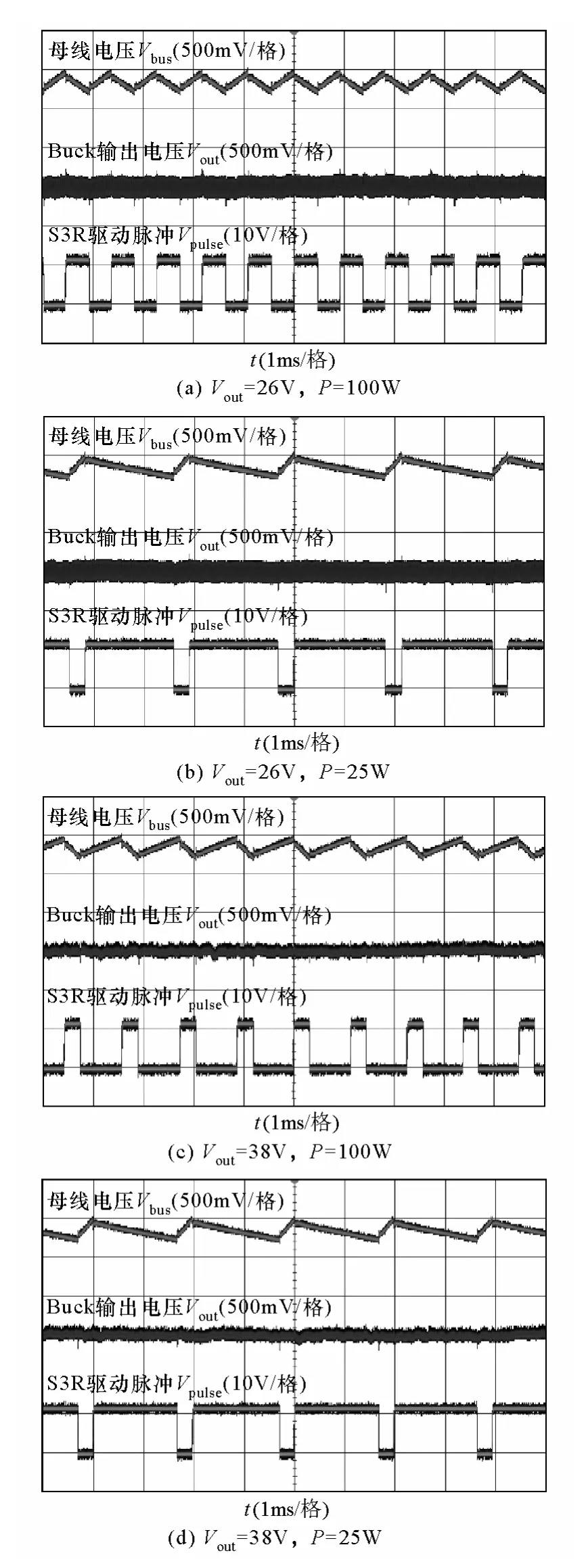
图10 加入前馈实验波形Fig.10 Waveforms with feedforward

由上述实验结果可知，当母线负载功率，即Buck 电路功率发生变化时，S3R 的分流频率变化，因此母线上的纹波频率发生变化，并且由于滞环控制的作用，对于固定功率点，分流频率也不是稳定的，脉冲周期有细微偏差。当Buck 电路无前馈控制时，Buck 电路输出电压中包含由输入电压引起的扰动，而当引入前馈控制器后，输入电压中的扰动对输出电压基本无影响，降低了噪声和损耗，由此验证了前馈控制电路方法设计的有效性。

6 结论

本文给出了DC-DC 变换器引入前馈控制时的系统框图，分析了调整变换器音频敏感率为零时前馈控制器需要满足的一般条件。介绍了航天PCU 系统的基本原理，针对全调节母线中的SR和BCR 级联系统进行了分析，以广泛应用于PCU 系统中BCR模块的Buck 电路拓扑为例，根据其前馈控制器表达式，介绍了一种能够根据输出侧蓄电池电压变化而自适应改变前馈控制器增益的控制方法。该控制方法可适用于Buck 变换器作为蓄电池充电模块时的一般性直流分布系统中。文章通过仿真和实验对理论分析进行了验证，结果表明该控制方法能够在输出侧有效抑制由输入电压纹波引起的扰动，降低了系统噪声和损耗，提高了系统的稳定性。

[1]Patel M R.Spacecraft power systems[M].United States:CRC Press Inc,2005.

[2]Capel A,O'Sullivan D,Marpinard J C.High-power conditioning for space applications[C].Proceedings of the IEEE,1988,76(4):391-408.

[3]Craig C S,Weinberg A H,Hall K W.The design and performance of a power system for the GALILEO system test bed (GSTB-V2/A)[C].Proceedings of Seventh European Space Power Conference (7th ESPC),2005:SP-589.

[4]Maset E,Ferrers A.5kW weinberg converter for battery discharging in high-power communications satellites[C].Proceedings of IEEE Power Electronics Specialist Conference,2005:69-75.

[5]Castiaux J P,Bury P,Liegeois B.A new generation of power conditioning modules for high power telecommunication spacecrafts[C].Proceedings of Fourth European Space Power Conference,1995:61-68.

[6]Picart G,Michoud V.Behavioural modeling of the spacbus 3000 power conditioning unit[C].Proceedings of Fourth European Space Power Conference(4th ESPC),1995:89-94.

[7]O’Sullivan D,Weinberg A H.The sequential switching shunt regulator(S3R)[C].ESTEC Spacecraft Power Conditioning Seminar,1977:123-131.

[8]Garrigos A,Blanes J M,Carrasco J A,et al.Hybrid photovoltaic-hydrogen power conditioning system[C].Proceedings of Ninth European Space Power Conference,2011:SP-690.

[9]Delepaut C.S3R stability margins and design guidelines[C].Proceedings of Eighth European Space Power Conference (8th ESPC),2008:SP-661.

[10]Maset E,Sanchis K E,Weinberg A H,et al.ION drive propulsion mpp power conditioning system without battery[C].Proceedings of Eighth European Space Power Conference (8th ESPC),2008.

[11]Kelkar S S,Lee F C.Adaptive input filter compensation for switching regulators[J].IEEE Transactions on Aerospace and Electronic Systems,1984,20(1):57-66.

[12]Otto D V.Reduction of switching regulator audiosusceptibility to zero[J].Electronics Letters,1986,22(8):441-442.

[13]Calderoni L,Pinola L,Varoli V.Optimal feedforward compensation for PWM DC/DC converters[C].Power Electronics Specialists Conference,1990.

[14]Arbetter B,Maksimovic D.Feedforward pulse width modulators for switching power converters[J].IEEE Transactions on Power Electronics,1997,12(2):361-368.

[15]Luciano C,Paolo D P,Alberto L.maimum power point tracker controller for unregulated bus architecture[C].Proceedings of Seventh European Space Power Conference,2005.

[16]Peter A,Craig C.Non-sequential power bus for LEO applications[C].Proceedings of Seventh European Space Power Conference,2005.

[17]Middlebrook R D.Input filter considerations in design and application of switching regulators[C].Proceedings of IEEE Industry Applications Society Annual Meeting,1976:366-382.