基于电流预测和虚拟过采样的数字滞环控制

刘全伟 邓 焰 胡义华 何湘宁

（浙江大学电气工程学院 杭州 310027）

1 引言

分布式发电单元如太阳能光伏发电、风力发电、燃料电池发电、微型燃气轮机发电等形式是现代微电网的重要组成部分[1]。这些发电形式都需要通过并网变换器将所产生的电能送入微电网。并网变换器的主要控制目标之一就是并网电流波形的质量，即保证并网电流的功率因数为1 且总的谐波畸变率低。

目前常见的并网变换器控制方法有滞环控制、三角载波比较PWM 控制、定时比较控制、无差拍控制、重复控制和单周控制等[2-14]。三角载波比较PWM 控制并网电流跟踪速度较慢；定时比较方法控制精度相对较低；无差拍控制以及重复控制都是基于被控对象精确数学模型建立的，其性能很大程度上依赖于被控对象模型的精度，而逆变器运行的开关特性以及死区时间等因素很难建立逆变器的精确模型；单周控制器由于复位脉冲存在延时，因此逆变器输出端存在直流偏置，而直流分量的存在会导致并网隔离变压器饱和，若加入电压补偿后系统较为复杂，且补偿量的大小和直流输入量有关[15]。

滞环控制不需要变换器的精确模型，且是无条件稳定的，因而比较适合于作为并网逆变器的控制器。然而传统的滞环控制方法也存在明显的缺点，如开关频率不固定，如式（1）所示，以及滤波器设计困难、滞环宽度难以确定等；其半周期开关次数总和如式（2）所示，最大开关频率如式（3）所示。文献[3]提出了三态滞环的控制策略，其最大开关频率和总开关频率只有两态滞环控制的 1/4。文献[16-18]都用不同的方法提出了变滞环宽度的恒频控制策略，其滞环宽度如式（4）所示。文献[15]提出了恒频固定滞环宽度的控制策略。文献[19]在功率因数校正中设计了电流脉动最小化的数字滞环控制策略。文献[20]提出了开通时间预测的数字滞环控制策略，但该方法需要在一个开关周期内过采样才能取得较好的实验波形。

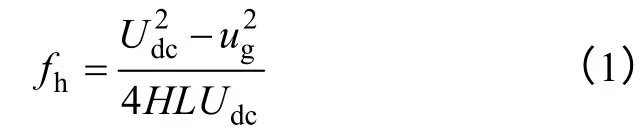
每半个正弦周期开关次数总和为

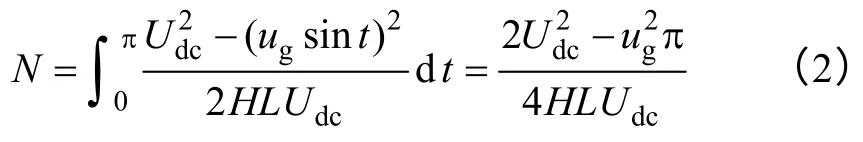
最大开关频率为

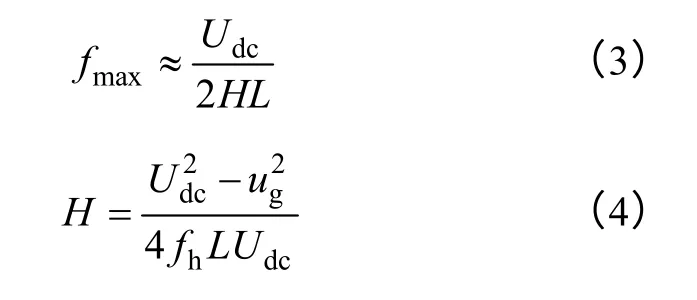
式中，ug为电网交流电压；H为滞环宽度；L为滤波电感；fh为开关频率；Udc为母线电压。

当式（1）中Udc、H、L固定时，网侧电压ug呈现正弦规律变化，在ug瞬时值较小时（即过零点附近）开关频率较高。为降低开关管频率，可以通过降低逆变器输入电压、增大滞环宽度以及增大电感量等方法来实现。但增大电感不仅会增加变换器的体积和成本，还会降低电流跟踪的快速性；增大滞环宽度会增加输出波形谐波含量。此外，在实际利用数字控制器实现滞环控制时，由于受采样频率限制，在采样时间内会出现电流上升或下降过冲，使滞环宽度在一定时间范围内失效，从而导致谐波比预期值大而无法满足工程要求。

为了克服上述普通数字滞环控制方法所存在的不足，本文在普通数字滞环控制的基础上提出了一种基于电流预测的数字滞环控制方式，并采用虚拟过采样的方法来弥补采样频率有限的不足。通过对电流的预测，选取跟随误差最小的开关组合作为下一拍的开关状态，从而提高输出电流波形质量。文中简述了前级为直流三电平结构的并网逆变器的工作原理；阐述了基于电流预测的数字滞环控制的原理；分析了采样频率对数字滞环控制的影响，并将虚拟过采样方法引入到本文所提出的数字滞环控制中，同时用仿真分析进行了验证；最后通过实验验证了本文所提出的控制方法的正确性。

2 直流三电平并网逆变器

直流三电平并网逆变器拓扑如图1a 所示，其中直流电压U1＜U2，通过开通或者关断S1和S2组合可以实现输出0（S1、S2都关断）、U1（S1导通、S2关断）、U2（S1关断、S2导通）、U1+U2（S1、S2都导通）四个电平，如图1b～图1e 所示。由S3、VDs3、S4、VDs4、S5、VDs5、S6、VDs6，构成电流型工频换相桥。

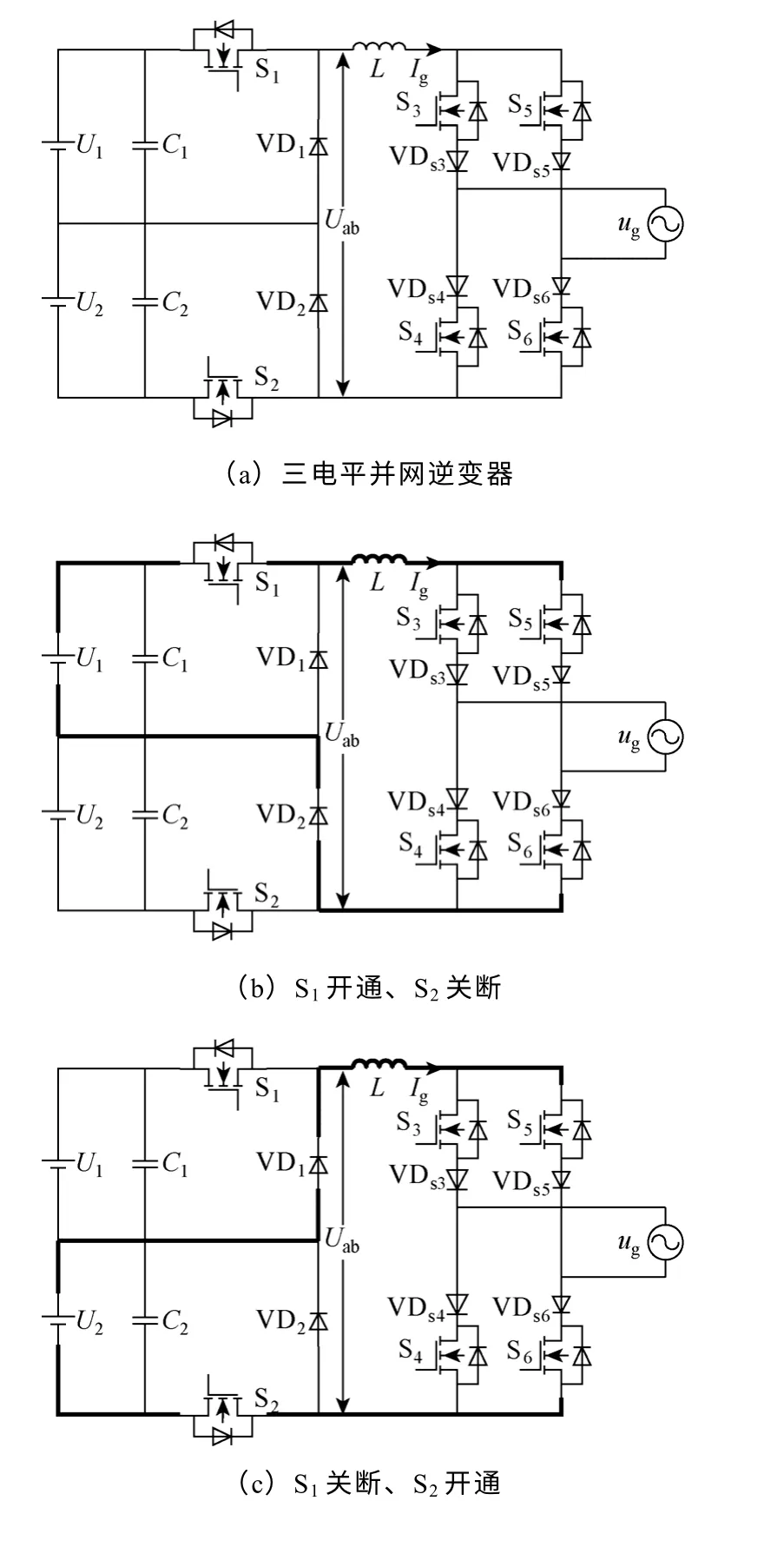
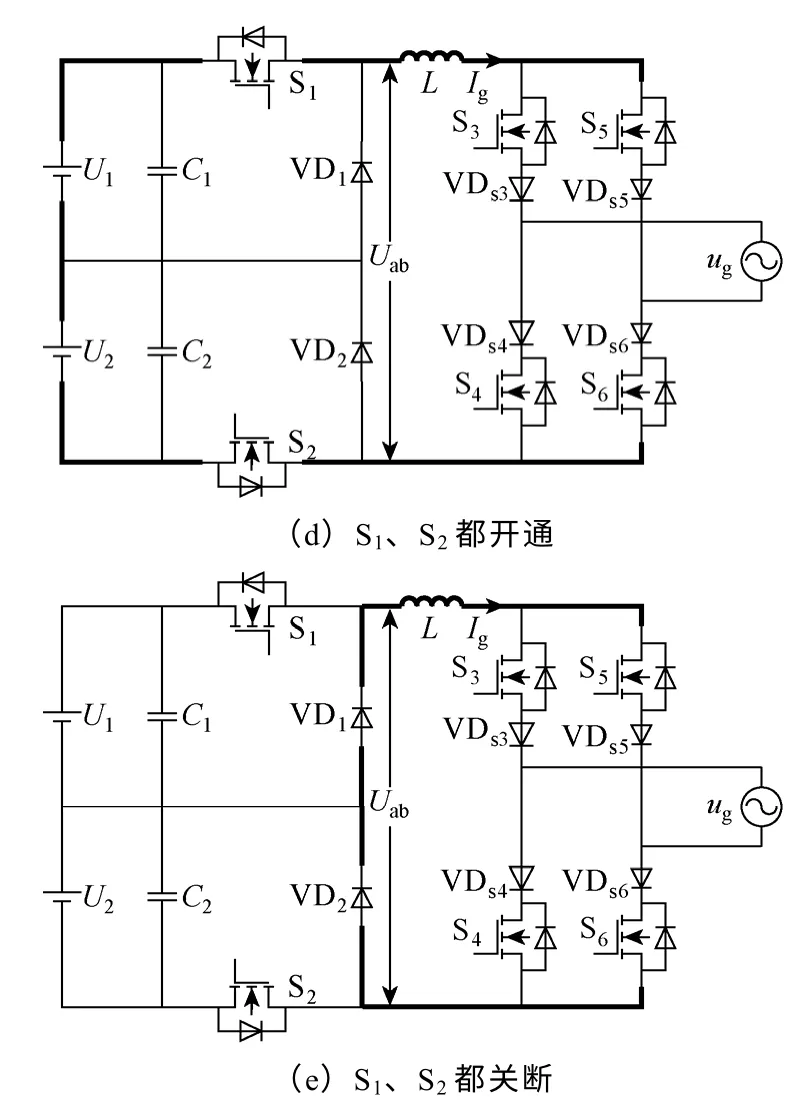
图1 并网拓扑结构Fig.1 Grid-connected inverter topology

3 电流预测滞环控制

在图1 所示的三电平并网逆变器电路中，由开关管S1、S2的不同开通、关断组合，可以给工频换相桥前端滤波电感L施加四种不同的直流电平，分别为0、U1、U2、U1+U2。滤波电感L的另一端通过工频换相桥连接至电网。电感电流的变化率由其两端的电压差所决定，如式（5），即由前端直流三电平结构的输出电平与电网电压共同决定。

当S1与S2组合出四种不同的电平时，电感L的电流变化率有四种不同的值，见表1。

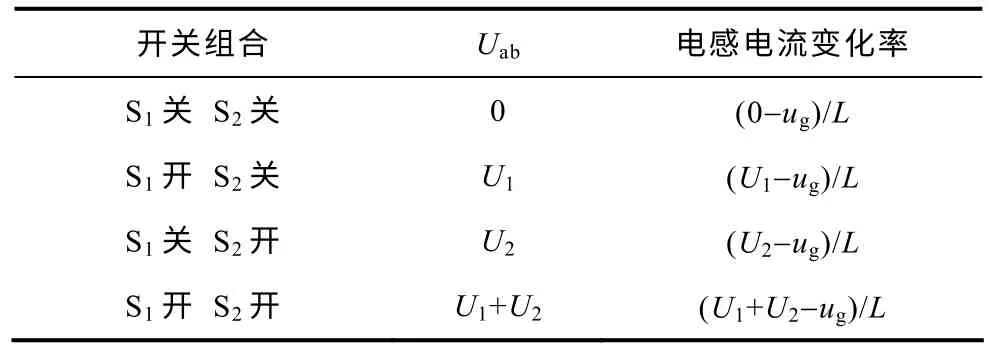
表1 直流三电平不同开关模态组合情况Tab.1 Different switching mode combinations

在第k拍采样点时，根据采样的电感电流Ig(k)、电网电压Ug(k)以及可能出现的四种不同直流电平，可以计算出在第k+1 拍时，电感电流可能的四种值，即图2 中所示的四个预测电流Ip1(k+1)～Ip4(k+1)。如式（6）所示，当Uab(k)分别为0、U1、U2、U1+U2时，第k+1 拍电感电流Ig(k+1)将有四种可能的值。

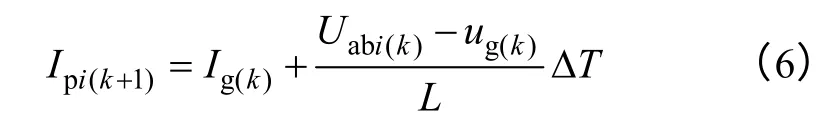
式中，Ig(k)为第k拍电感电流采样值，ug(k)为第k拍的电网电压采样值，Uabi(k)为第k拍第i种开关组合所对应的直流电压，Ipi(k+1)为第k+1 拍第i种电感电流预测值，ΔT为采样周期。

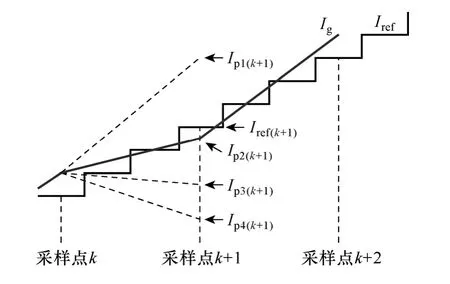
图2 基于电流预测的滞环控制Fig.2 Current prediction hysteresis control

为了使电感电流更精确地跟踪电流参考值Iref，应在第k+1 拍的四种可能的电感电流值中选取最接近Iref(k+1)所对应的开关组合。即选取第i种开关组合，使得式（7）最小，由此可以确定第k拍的S1、S2的开关模态。

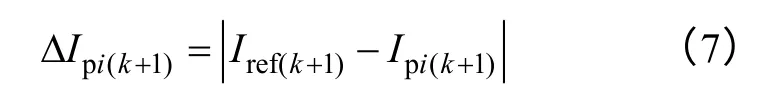
同理，在第k+1 拍采样点时，按照相同的方法，可以计算出最优的开关组合作为第k+1 拍的S1、S2的开关模态。

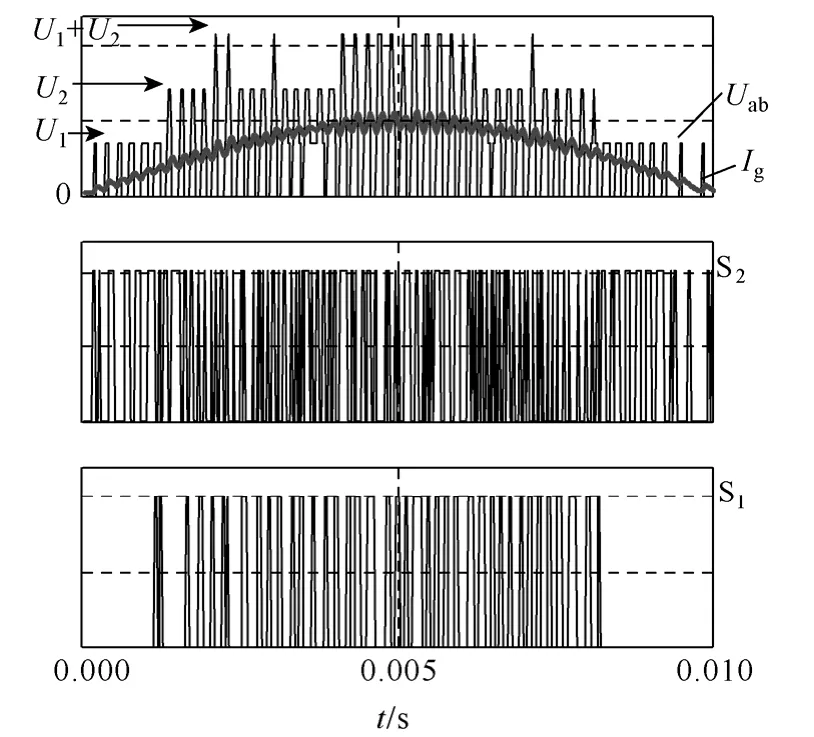
图3 电流预测滞环控制仿真波形Fig.3 Current prediction hysteresis control simulation waveforms

图3 所示为上述基于电流预测的数字滞环控制的仿真波形，其中电感电流指令为工频正弦波半波。可以看到，电感电流为光滑的正弦半波，直流三电平输出电压Uab和前述理论分析一致，共有四个电平值，其分布规律类似于多电平SPWM 调制。

上述仿真分析表明，本文所提出的基于电流预测的数字滞环控制针对有多个电平的变换器是非常有效的，它能根据预测的电流值选择最优的开关组合，从而使得实际电流以误差最小的方式跟踪电流指令值。

4 基于电流预测和虚拟过采样的数字滞环控制

在实际的数字滞环控制中采样频率对控制性能起着重要的作用。针对本文所提出的电流预测滞环控制，每一拍电感电流增量为

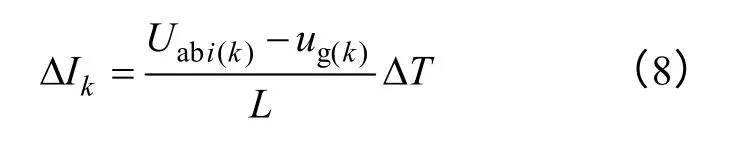
当控制程序根据电流预测算法给出最优开关组合后，Uabi(k)已确定。可以看到，此时电流的波动值仍然受采样周期ΔT的限制。当采样周期较大时，最终使得电感电流纹波仍然较大，难以获得理想的控制性能，后文中实验验证也充分表明了这一点。

为了解决控制性能和采样频率限制这一对矛盾，本文在电流预测滞环控制的基础上，引入了虚拟过采样算法。如图4 所示，在两个真实的采样点之间，插入m个虚拟采样点，在虚拟采样点并不进行反馈信号的采样，而是用式（6）给出的电感电流预测值代替真实的电感电流反馈值，继续进行电流预测滞环控制。到下一个真实采样点时，又按照真实的电流采样值进行电流预测控制，从而可以提高等效采样频率，进一步改善控制性能，提高电感电流波形的质量。

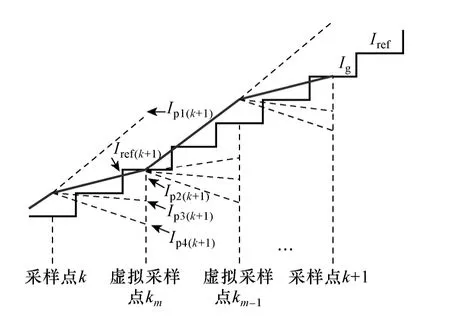
图4 基于电流预测和虚拟过采样的数字滞环控制Fig.4 Current prediction and virtual over-sampling based hysteresis control

从图4 中可以看到，在真实采样点之间插入虚拟采样点后，在不提高采样频率的条件下，电感电流纹波变得更小，能够更加精确地跟踪电流指令值。图5 给出了基于电流预测和虚拟过采样的数字滞环控制仿真分析波形。可以看到，在采样频率不变的前提下，图5 中的等效开关频率较图3 中的高，电感电流开关纹波更小，波形质量改善明显。

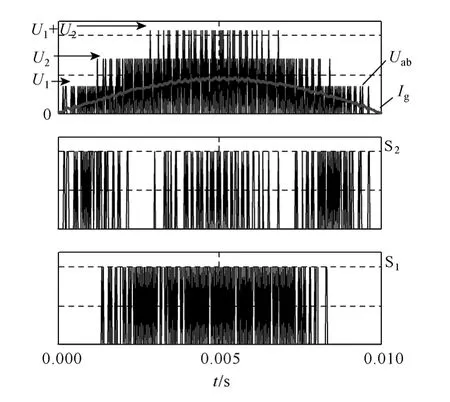
图5 电流预测和虚拟过采样的数字滞环控制仿真波形Fig.5 Current prediction and virtual over-sampling based hysteresis control simulation waveforms

5 实验验证

为了验证本文所提出的控制算法，研制了一台实验样机。电路结构如图1a 所示，以TMS320LF2812为控制器，实现本文提出的控制策略。主电路中S1和S2所用开关管为IRFP460，输入电容C1和C2为400V/450μF，VDs3～VDs6所用二极管为MUR1560，电感L为2.5mH，电压U1、U2分别为120V、240V。以下数字滞环控制采样频率均为33.3kHz。

将S1与S2同时开通关断来实现普通两态数字滞环控制，当S1与S2同时开通时，电压Uab等于母线电压U1+U2，当S1与S2同时关断时电压Uab=0。图6a是传统两态数字滞环控制的并网电流波形，图6b是其放大波形，其中通道1和2 分别是S1和S2的开关信号，通道3是并网电流，图6c是并网电流的谐波频谱。从图中可以看出两态数字滞环控制受采样频率和环宽的限制，电流纹波较大，并网电流THD 较大。

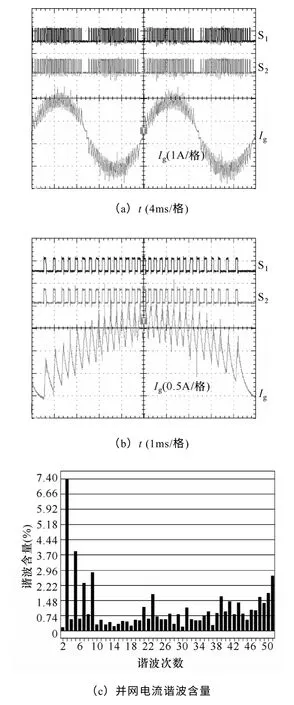
图6 普通两态滞环控制实验结果Fig.6 Hysteresis control experimental waveforms

图7 示出了本文所提出的电流预测滞环控制算法的实验波形。图7a是并网电流波形，图7b是其放大波形，其中通道1和2 分别是S1和S2的开关信号，通道3是并网电流，图7c是并网电流的谐波频谱。可以看到，图7a 中并网电流为比较光滑的正弦波，与图3 中所示的仿真结果较为吻合，表明电流预测滞环控制算法的正确性；从图7b 的放大波形与图6b 的对比中可以看到，本文所提出的电流预测滞环控制算法可以明显改善电流波形。然而受限于采样频率，电感电流仍含有一定量的谐波。

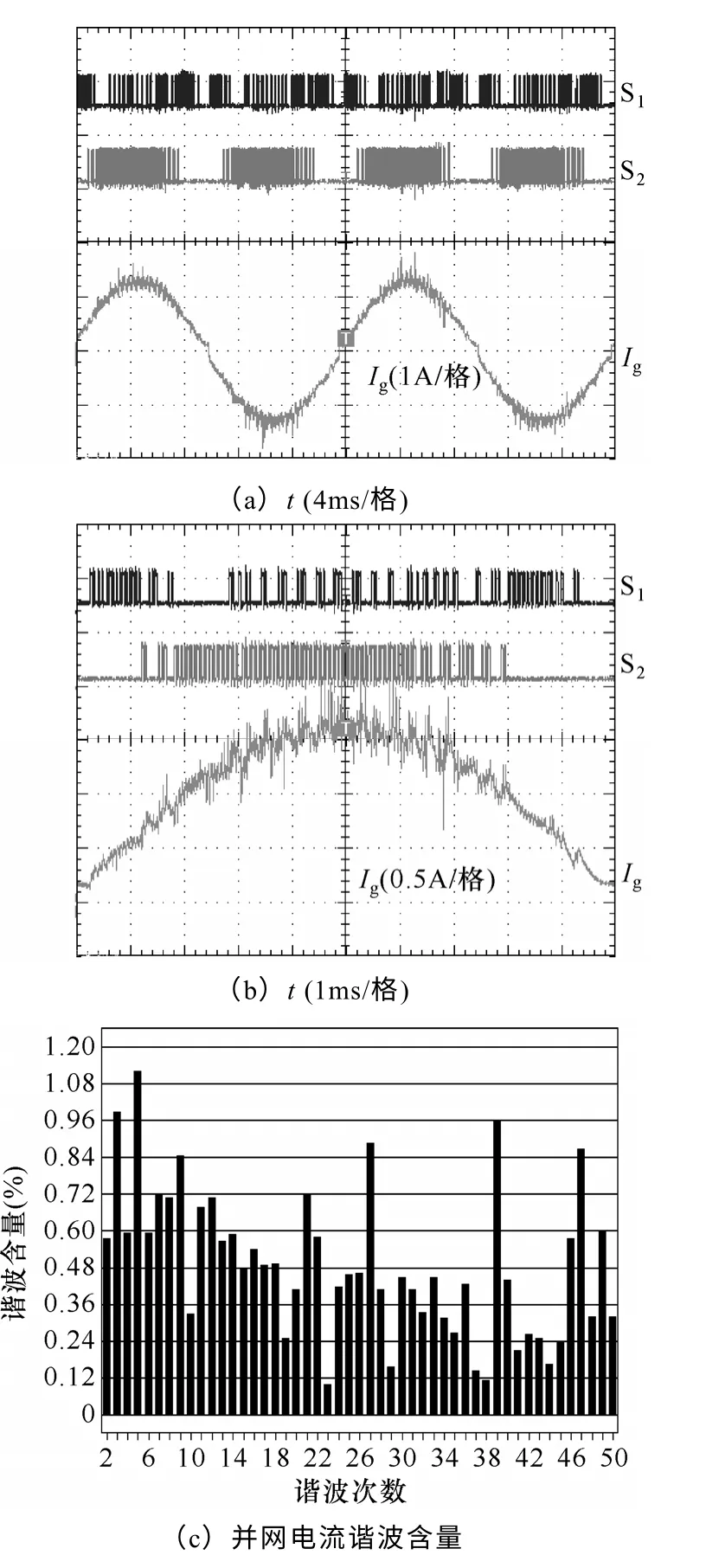
图7 电流预测滞环控制实验结果Fig.7 Current prediction hysteresis control experimental results

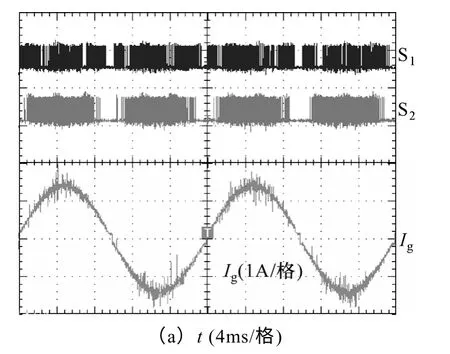
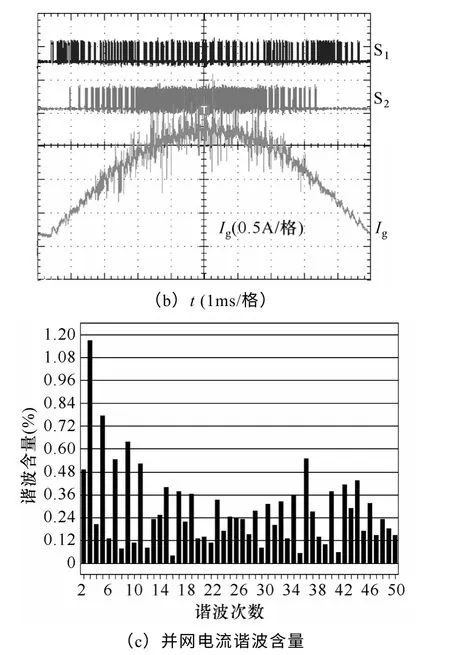
图8 基于电流预测和虚拟过采样的数字滞环控制实验结果Fig.8 Current predict and virtual over-sampling hysteresis control experimental results

图8 示出了基于电流预测和虚拟过采样算法的数字滞环控制的实验波形。实验程序在33.3kHz 采样频率的基础上，每两个真实采样点之间插入一个虚拟过采样点。可以看到，在电流预测滞环控制的基础上，引入虚拟过采样弥补采样频率较低的不足可以有效改善控制器的性能。从图7和图8 的对比中可以明显看出，在相同的采样频率下，加入虚拟过采样后的电流预测滞环控制可以较好的改善电流波形。同时，等效开关频率也有所提高。

表2 为这三种数字滞环控制算法在相同的采样频率下的并网电流THD。可以看到，电流预测滞环算法可以显著减小并网电流THD，加入虚拟过采样算法后，可以进一步减小并网电流THD。

表2 三种滞环算法控制性能Tab.2 Performance of three type of hysteresis control

上述实验结果中，在相同的采样频率下，传统数字滞环控制受限于滞环带宽与电流变化率，等效开关频率较低，且Uab只有两个电平，电流纹波很大，图6c 也显示出该控制策略下并网电流含大量的低次谐波；基于电流预测的数字滞环控制优化了直流级的开关组合，使得并网电流以误差最小的方式跟踪指令电流，且Uab被控制为多电平形式，因而该控制策略下并网电流谐波相对于传统滞环控制有较大的改善，图7c 中的低次谐波大为减小；加入了虚拟过采样算法的数字滞环控制算法使得实际采样频率不变的情况下，等效采样频率得以提高，因而并网电流谐波得到进一步改善，图7c和图8c 的对比可以看到虚拟过采样算法的加入可以进一步降低谐波含量。

6 结论

本文研究了一种基于电流预测和虚拟过采样算法的数字滞环控制策略，并对其进行了仿真分析和实验验证，结论如下：

（1）在具有多个输出电平的变换器控制中，根据预测的电流值选择最优的开关组合，从而使得实际电流以误差最小的方式跟踪电流指令值。该算法无需设置滞环环宽，算法简单易行。

（2）在真实采样频率有限的情况下，根据变换器模型的计算值，在每两个真实采样点之间插入多个虚拟采样点，实现虚拟过采样，可以提高等效采样频率，改善输出波形质量。

本文所提出了基于电流预测和虚拟过采样算法的数字滞环控制方法不仅适用于本文的拓扑结构，对具有多个输出电平的其他类型变换器同样具有普适性。

[1]Lasseter R H.Micro grids[C].IEEE Power Engineering Society Winter Meeting,2002:305-308.

[2]王建华,张方华,龚春英,等.滞环电流控制逆变器建模及分析[J].电工技术学报,2010,25(6):63-69.Wang Jianhua,Zhang Fanghua,Gong Chunying,et al.Modeling and analysis of inverter with hysteretic current control[J].Transactions of China Electrotechnical Society,2010,25(6):63-69.

[3]顾和荣,杨子龙,邬伟扬.并网逆变器输出电流滞环跟踪控制技术研究[J].中国电机工程学报,2006,26(9):108-112.Gu Herong,Yang Zilong,Wu Weiyang.Research on hysteresis-band current tracking control of gridconnected inverter[J].Proceedings of the CSEE,2006,26(9):108-112.

[4]洪峰,刘军.滞环电流控制型双 BUCK 逆变器[J].电工技术学报,2004,19(8):73-77.Hong Feng,Liu Jun.Hysteresis current controled dual buck half bridge inverter[J].Transactions of China Electrotechnical Society,2004,19(8):73-77.

[5]范小波,张代润.光伏并网逆变器数字滞环控制的研究[J].电力电子技术,2006,40(6):46-48.Fan Xiaobo,Zhang Dairun.Research on digital hysteresis control for grid-connected PV inverter[J].Transactions of China Electrotechnical Society,2006,40(6):46-48.

[6]Krismadinata,Rahim N A,Selvaraj J.Implementation of hysteresis current control for single-phase grid connected inverter[C].7th International Conference on Power Electronics and Drive Systems,2007:1097-1101.

[7]Maswood A I,Liu Fangrui.A unity-power-factor converter using the synchronous reference frame based hysteresis current control[J].IEEE Transactions on Industry Applications,2007,43(2):593-599.

[8]魏克新,纪世忠,于洋.三相PWM 整流器滞环控制改进方法的研究[J].电力电子技术,2011,45(9):114-116.Wei Kexin,Ji Shizhong,Yu Yang.Research on improved hysteresis control strategy of three-phase PWM rectifier[J].Transactions of China Electrotechnical Society,2011,45(9):114-116.

[9]刘飞,查晓明,周彦,等.基于极点配置与重复控制相结合的三相光伏发电系统的并网策略[J].电工技术学报,2008,23(12):130-136.Liu Fei,Zha Xiaoming,Zhou Yan,et al.Research on grid-connected strategy combining pole-assignment and repetitive control in three-phase photovoltaic system[J].Transactions of China Electrotechnical Society,2008,23(12):130-136.

[10]Yang Chen,Smedley K M.A cost-effective singlestage inverter with maximum power point tracking[J].IEEE Transactions on Power Electronics,2004,19(5):1289-1294.

[11]Femia N,Granozio D,Petrone G,et al.Optimized one-cycle control in photovoltaic grid connected applications[J].IEEE Transactions on Aerospace and Electronic Systems,2006,42(3):954-972.

[12]蒋立,郑建勇.Z 源光伏并网直接电流单周控制系统[J].电力系统自动化,2008,32(22):87-90.Jiang Li,Zheng Jianyong.A direct current one-cycle control method for Z-source grid-connected photovoltaic system[J].Automation of Electric Power Systems,2008,32(22):87-90.

[13]周雒维,龚伟,苏向丰.一种改进的单周控制的开关功率放大器[J].电工技术学报,2004,19(5):106-110.Zhou Luowei,Gong Wei,Su Xiangfeng.An improved switching power amplifier with one cycle control[J].Transactions of China Electrotechnical Society,2004,19(5):106-110.

[14]唐欣,罗安.基于重复控制的有源滤波器的三态滞环控制方法[J].电工技术学报,2009,24(9):134-139.Tang Xin,Luo An.Repetitive control based threestate hysterisis control of a single-phase active filter[J].Transactions of China Electrotechnical Society,2009,24(9):134-139.

[15]Ho C N M,Cheung V S P,Chung H S H.Constantfrequency hysteresis current control of grid-connected VSI without bandwidth control[J].IEEE Transactions on Power Electronics,2009,24(11):2484-2495.

[16]Buso S,Fasolo S,Malesani L,et al.A dead-beat adaptive hysteresis current control[J].IEEE Transactions on Industry Applications,2000,36(4):1174-1180.

[17]Genping Wang,Lingzhi Yi,Xiao Zou,et al.The design of constant frequency hysteresis current controller with voltage space vector in PV gridconnected inverter[C].Automation Congress 2008,WAC 2008 World,2008:1-5.

[18]洪峰,单任仲,王慧贞,等.一种变环宽准恒频电流滞环控制方法[J].电工技术学报,2009,24(1):115-119.Hong Feng,Shan Renzhong,Wang Huizhen,et al.A varied hysteresis-band current controller with fixed switching frequency[J].Transactions of China Electrotechnical Society,2009,24(1):115-119.

[19]胡庆波,瞿博,吕征宇.一种新颖的应用于PFC 电路中电流控制的方法[J].中国电机工程学报,2006,26(3):64-68.Hu Qingbo,Qu Bo,Lü Zhengyu.A novel method for current control used in PFC converter[J].Proceedings of the CSEE,2006,26(3):64-68.

[20]Stefanutti W,Mattavelli P.Fully digital hysteresis modulation with switching-time prediction[J].IEEE Transactions on Industry Applications,2006,42(3):763-769.