零扰动补偿控制电流模式Buck 变换器

卢伟国 栗安鑫 周雒维 毕 凯

（重庆大学输配电装备及系统安全与新技术国家重点实验室 重庆 400044）

1 引言

峰值电流模式具有动态响应速度快、补偿电路简单及限流等特点，在电力电子开关变换器系统中具有广泛应用[1,2,5,6]。但随着系统参数变化，峰值电流模式开关功率变换器系统不可避免的存在分岔和混沌等不稳定行为[2-5]。次谐波不稳定行为是一类典型的分岔行为[5]，工程上一般采用斜坡补偿控制来抑制[5-11]。线性斜坡补偿存在补偿度问题，过度补偿会降低系统输出电流能力和系统动态特性，甚至造成波形畸变[6,7]，为此有关学者提出分段线性斜坡补偿[8,9]和自适应斜坡补偿[10,11]的改进方式。但是，开环型斜坡补偿的实质是通过在开关切换时刻减小参考电流值来确保系统稳定性，因此斜坡补偿方式始终会牺牲系统参考电流的稳定工作范围。事实上，如果施加的补偿控制信号在稳态时近似为零，那么所施加控制可保证系统在原有工作范围内稳定运行，如此则可避免现有斜坡补偿的补偿度问题，此类控制具备零扰动补偿特性。借鉴现有分岔和混沌控制思想[12]，闭环型的延迟反馈控制[13]和滤波器形式[14]可实现零扰动补偿控制，但模拟电路实现延迟反馈控制比较困难，滤波器式控制的电路结构较为复杂。总的来看，这两类零扰动控制的扰动控制量期望在稳态任何时刻均近似为零，因此其物理实现形式会比较复杂，并且会在系统中增加新的延迟因子和状态变量，使系统的建模和稳定性分析变得复杂。注意到，在开关变换器中，系统控制信号即占空比仅由各周期开关切换时刻的反馈量决定。如此，系统被控稳定后，只需保证开关切换时刻的扰动控制量趋近为零，即可满足零扰动补偿控制要求，此类情形可视为一类简化的零扰动补偿控制条件。

基于上述，本文拟结合典型峰值电流模式Buck变换器，依据简化的零扰动补偿控制条件构建出反馈型零扰动补偿控制电路。同时，利用开关变换器系统的周期态特性，引入傅里叶级数思想，导出系统的边界分岔方程，确定出零扰动控制增益参量与参考电压分岔点间的量化关系，进而给出控制参数的可控范围。最后通过有关仿真和实验以验证所提控制思路有效性。

2 控制思路

双闭环峰值电流模式Buck 变换器电路如图1所示。其中，输入电压vin的稳态值记为Vin，输出电压vo的稳态值为Vo，vD为二极管端电压，iL为电感电流（采样电流），r为采样电阻，ur为采样电阻两端的电压。控制电路中，Vref为外加的参考电压，iref为内环参考电流，CLK 为时钟信号，Δi为零扰动控制电流信号（综合输入输出实现），ir'ef为比较器的输入控制信号。

图1 峰值电流模式Buck 变换器Fig.1 Peak-current mode Buck converter

电压外环采用PI 调节器，因此内环参考电流iref为

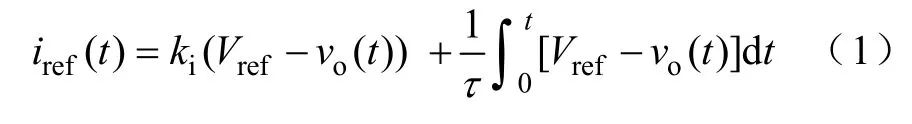
式中，ki和τ为PI 调节器参数；d是系统占空比。

当外环参考电压增大时，内环参考电流iref也会同步增大，由此可能会造成系统出现不稳定的次谐波分岔行为[12]，图中零扰动控制Δi的引入就是为了控制系统的不稳定行为。零扰动控制的实现思路如下，依据引言中简化的零扰动补偿控制条件Δi(DT)≈0（稳态时），扰动控制信号Δi(t) 可按下式构造得到。

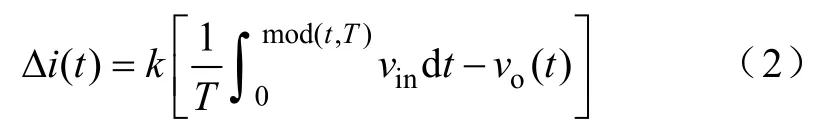
式中，k是零扰动控制信号比例增益（控制参数）；T为开关周期。

Buck 变换器在稳态情况下工作时，输入电压和输出电压的稳态关系满足:DVin=Vo，D为稳定占空比。同时，认为输入电压变化很小，有vin≈Vin。稳态情况下，式（2）所示的扰动控制信号Δi(t) 在开关切换时刻满足

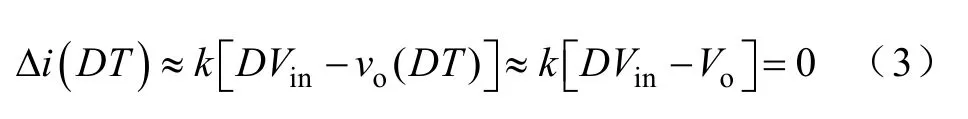
基于式（2）可构造出零扰动控制结构如图 2所示。

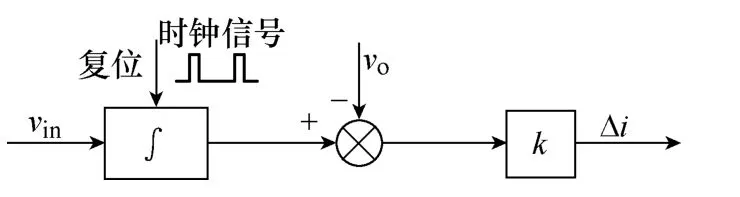
图2 零扰动补偿控制结构Fig.2 Zero-perturbation control block

对图2 所示的零扰动控制而言，控制参数k的大小决定了扰动控制能否有效控制系统稳定。控制参数k与系统边界分岔参考电压Vrefb（不稳定边界）相对应，若能构建出控制参数k与分岔点参考电压Vrefb的量化关系，即可确定控制参数k的可控范围。下面的工作就是从理论上导出控制参数k与Vrefb的数学关系式，从而为控制参数选择提供理论依据。

3 控制参数选择

对于峰值电流模式Buck 变换器系统而言，当系统中参考电流较小（记为iref1）时，系统处于稳定的单周期状态（期望状态），电感电流和二极管端电压波形如图3a 所示。研究表明[2]:随着参考电流iref的增大，系统会出现不稳定的次谐波行为（二周期态）。图3b 给出了由单周期态过渡到二周期态时的电感电流和二极管电压波形，此时电感电流记为iref2。图3 中，δ是dT的小扰动量。当δ→0，图3b 的iref2为临界二周期态对应的参考电流，也就是分岔边界点参考电流irefb，此时记分岔边界占空比为db，分岔边界参考电压为Vrefb。

图3 电感电流和二极管两端电压波形Fig.3 Waveforms of the induct or current and the diode voltage for period-1 state and period-2 state

结合图3 可知，二极管电压vD为连续的周期性方波信号，可表示为占空比d、输入电压Vin的傅里叶级数展开形式[14]，具体可表示为

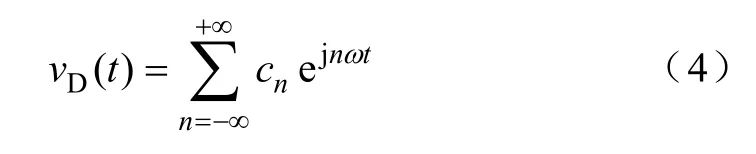
式中，cn为傅里叶级数的系数；ω为系统的开关角频率，即ω=2π/T。

对于图1 所示的峰值电流模式Buck 变换器而言，可用图4 所示的等效结构框图来描述。Buck 变换器电路中非线性特性集中体现在PWM 部分。

图4 峰值电流模式Buck 变换器等效结构框图Fig.4 The block diagram of the current-mode Buck converter

图4 中，ei为电流误差信号，用以决定Buck电路的占空比d。G1(jω) 为输出电压Vo(jω) 到二极管电压VD(jω) 的传递函数，G2(jω) 为电感电流IL(jω) 到二极管电压VD(jω) 的传递函数，Gc(jω)为PI 调节控制器的传递函数，相应传递函数如下:

式中，ki和τ为PI 调节器参数。

考虑到vD可以描述为傅里叶级数，结合图4 中的输出电压vo、电感电流iL与二极管电压vD之间的频域对应关系，以及文献[14]中的谐波平衡法，扰动控制量和参考电流可以表示为傅里叶级数形式。

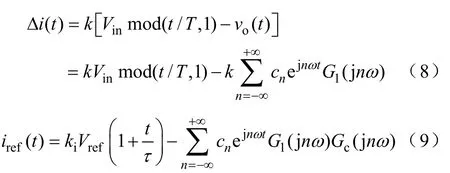
此外，由图3a 对应的单周期状态情形，开关切换时刻O 点有电流平衡方程

结合式（9）和式（10），可得

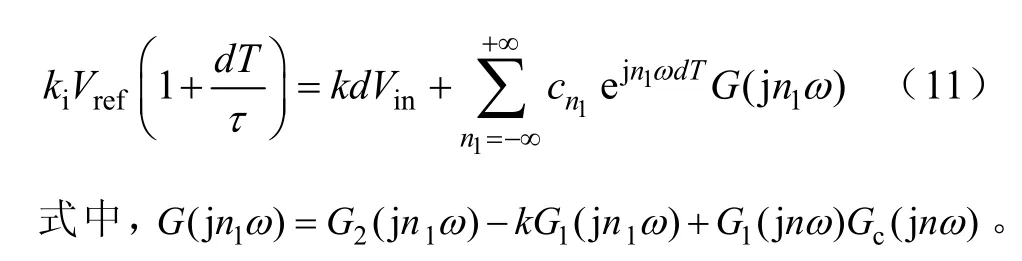
同理，图3b 中临界二周期状态P、Q 点电流平衡方程，有

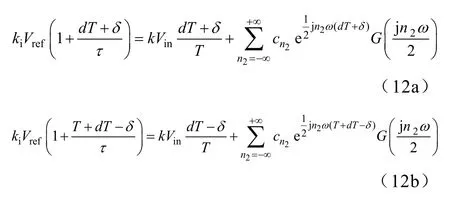
式中

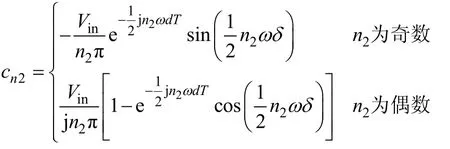
式（12b）中，参考电压经一个开关周期的积分值与右侧级数的部分直流量（n2=0）存在平衡，数学处理上可忽略该部分分量。此外，考虑到时间常数τ比开关周期要大得多，如此可得扰动信号δ的简化等效平衡方程如下:

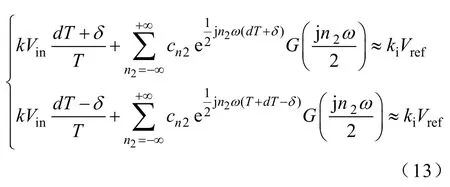
将式（13）中两个方程相减，并令扰动量δ→0，可得系统控制参数k与边界分岔占空比db的关系式如下:

式（14）是近似等效结果，该结果大致表明系统输入电压Vin对边界分岔占空比db影响不大。结合式（11）可进一步得出边界分岔参考电压Vrefb与边界分岔占空比db之间的关系式

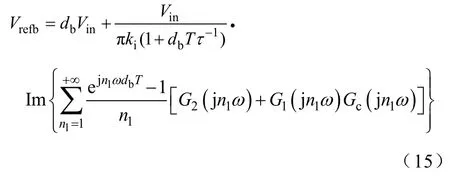
综合式（14）和式（15），可得到系统的边界分岔参考电压Vrefb与控制参数k之间的量化关系曲线，由此边界可以确定出控制参数k的可控范围。

4 仿真计算分析

系统电路参数选择为:Vin=10V，L=1.4mH，C=100μF，R=10Ω，f=4kHz，采样电阻r=0.5Ω，PI调节器参数取ki=1，τ=2ms。

4.1 分岔边界计算结果

结合式（14）和式（15），数值计算得到参考电压Vref的边界分岔曲线如图5 所示，图中描述了系统参考电压稳定边界Vrefb与控制参数k的对应关系。

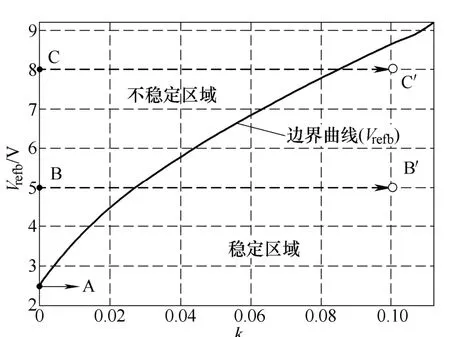
图5 参考电压分岔边界曲线Fig.5 Bifurcation boundary of reference voltage

由图5 可知，系统未施加零扰动控制信号（k=0）时，系统在参考电压Vref大约为2.5V 开始出现不稳定的次谐波行为，随着参考电压Vref的进一步增大，系统纹波经多周期态恶化至混沌态。图中，A点（Vrefb≈2.5V）标示为系统的边界分岔点，B 点（Vref≈5V）和C 点（Vref≈8V）均为系统的不稳定工作点（没有施加零扰动控制）。当系统施加的零扰动控制信号（k=0.1）后，系统对应的边界分岔点Vrefb可达到9V 以上，即表明此时系统能在参考电压Vref为 9V 范围内稳定工作。控制后，系统不稳定工作点B 和C 可分别被控制到稳定工作点B'和C'。图5 从数值理论计算角度说明零扰动控制能实现对系统不稳定行为的抑制。

4.2 仿真结果分析

图6a 和图6b 分别为参考电压Vref=5V 和Vref=8V 时，t=0.05s 时刻施加k=0.1 零扰动控制信号的输出电压vo、电感电流iL和零扰动控制信号Δi的仿真波形；图6c 为Vref=5V，k=0.1 时，系统被控稳定后的输出电压vo、电感电流iL和零扰动控制信号Δi局部放大波形。

由图6a 和图6b 可知，未施加零扰动控制，参考电压Vref为5V 和8V 时（对应图5 的不稳定工作点B 和C），系统工作在不稳定态。当施加k=0.1 的零扰动控制信号后，系统稳定至单周期态工作点B′和C′。图6c 表明，系统稳定工作后，扰动控制信号在开关切换时刻近乎为零（Δi（DT）≈0），充分证实了所施加控制的零扰动控制特性。仿真结果与理论计算结果（见图5）相吻合，而工作点C→C′的有效稳定控制表明所提控制具有较大的稳定范围。

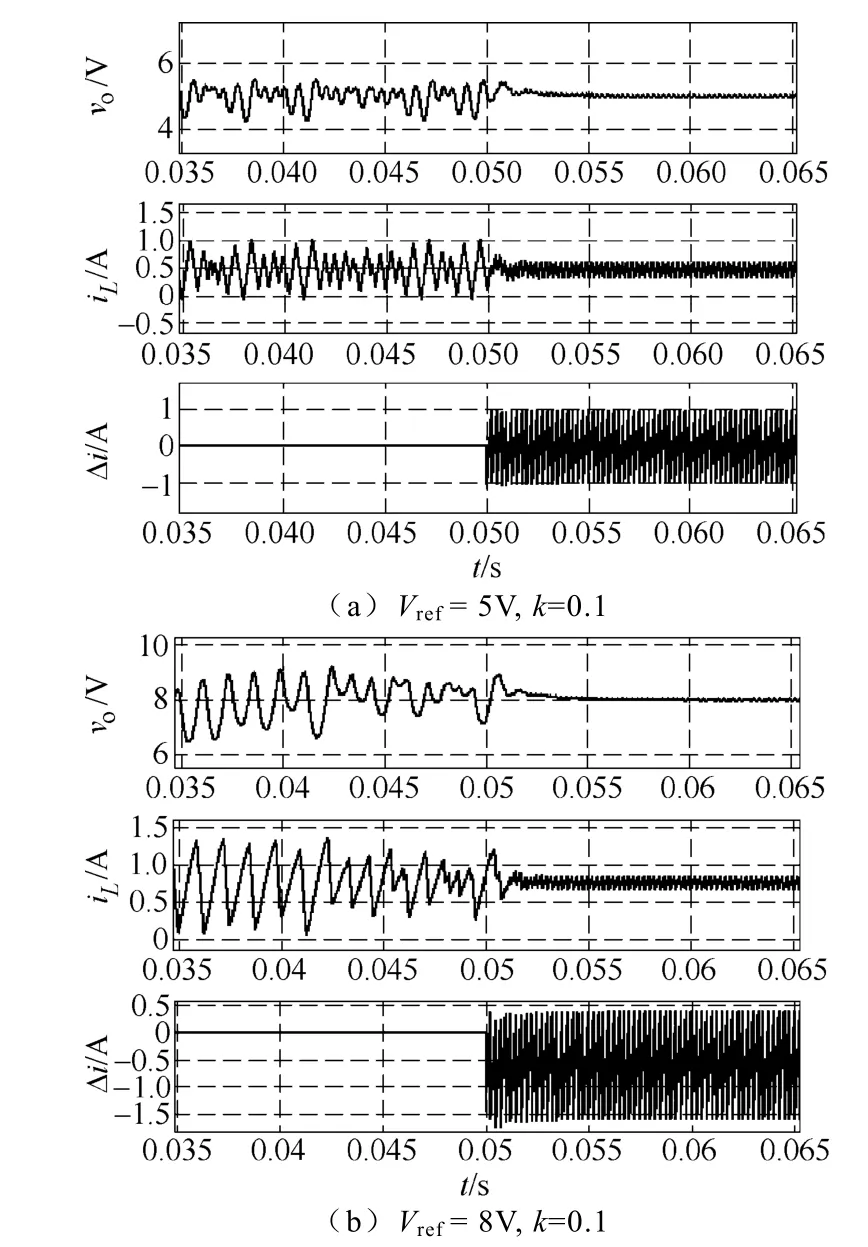
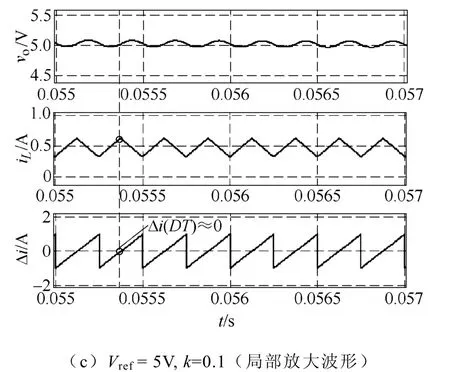
图6 施加零扰动控制前后仿真波形Fig.6 Simulation waveforms for Vref=5V and k=0.1,Vref=8V and k=0.1 and enlarged waveforms after control

5 实验结果分析

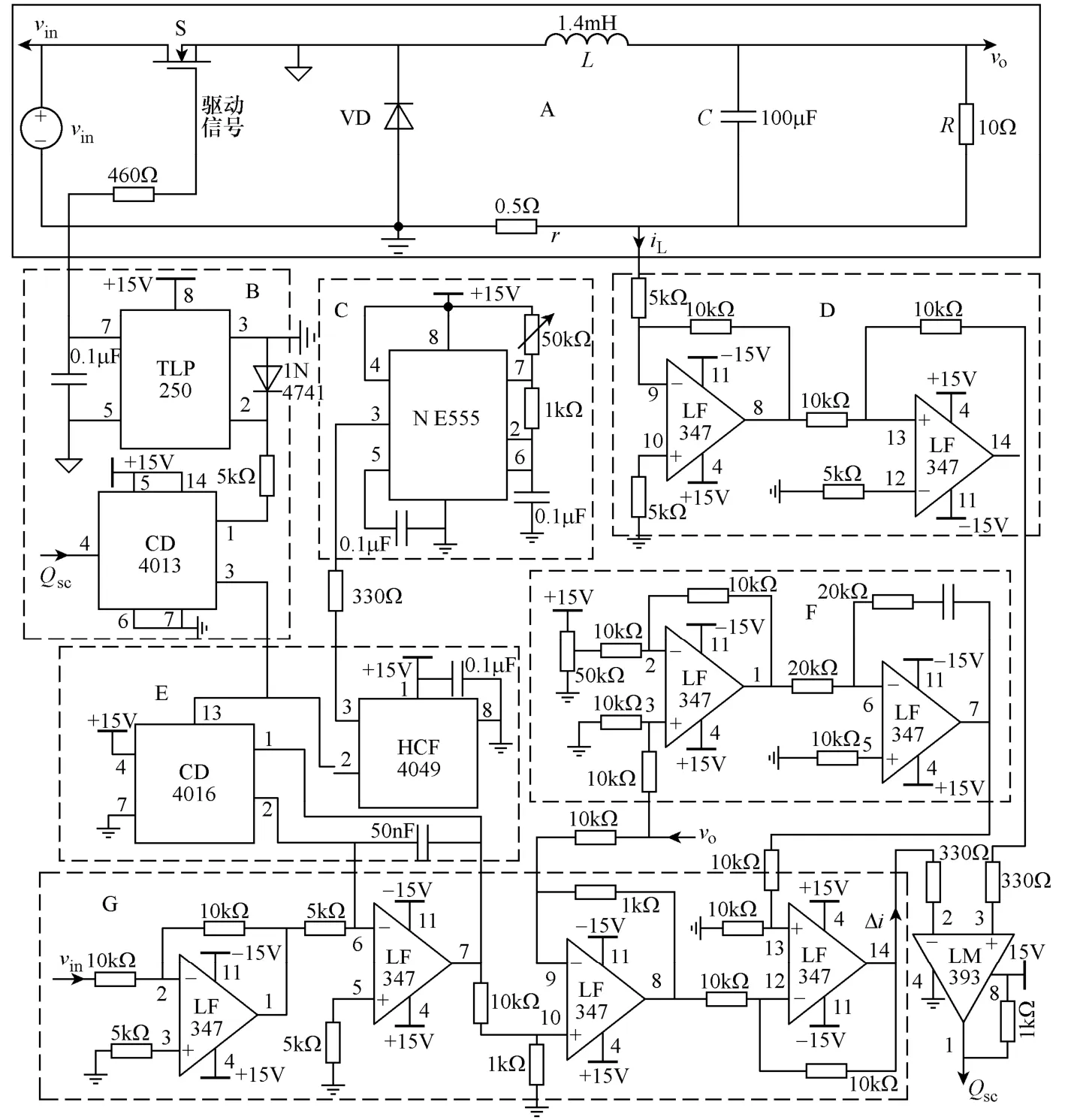
图7 实验电路原理图Fig.7 Experiment circuit schematic diagram

实验电路原理图如图7 所示，参数与仿真参数选取得一致。系统原理图可以描述为A～G 七部分，其中，A 部分为主电路，电压vin由直流电压源产生，开关管 S 的型号为 IRF530，其驱动芯片为TLP250，采样电阻r选择0.5Ω 精密电阻；B 部分为驱动信号产生电路；C 部分为555 定时器构建的时钟信号电路；D 为电感电流iL采样电路；E 部分为复位信号电路，由芯片CD4016 和CD4049 实现；F 为PI 补偿电路。此外，G 为本文所提的零扰动补偿控制电路，电路实现简单。

在实验结果分析中，同样选择参考电压Vref≈5V和Vref≈8V 为观察点，图8 和图9 给出了施加k≈ 0.1的扰动控制信号前后，输出电压vo、电感电流iL和零扰动控制信号Δi的实验波形。其中，图8a 和图9a 为未施加零扰动控制时的实验波形，图8b 和图9b 为施加零扰动控制后的实验波形。图8c 为Vref≈5V 时系统被控稳定后，输出电压vo、电感电流iL和零扰动控制信号Δi局部放大实验波形。上述实验结果与仿真结果大体吻合，验证了合适的零扰动控制信号可稳定系统到期望的单周期状态工作，且不改变系统的稳态工作点。

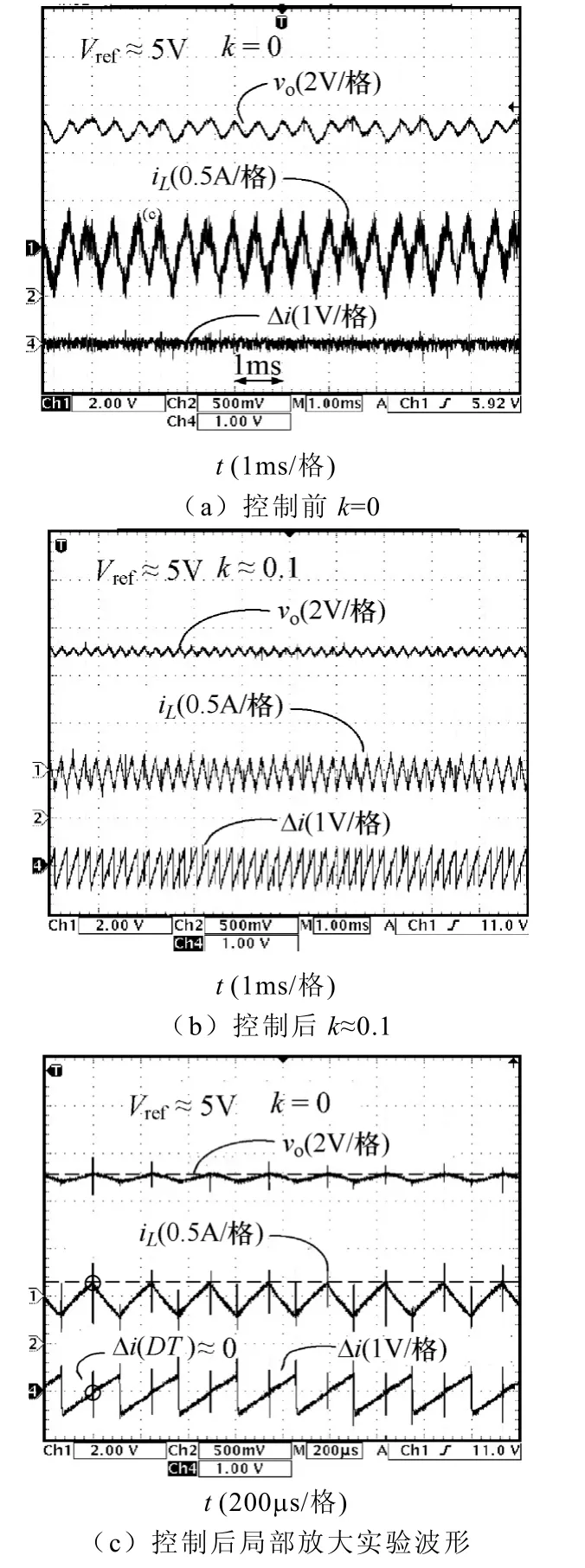
图8 Vref≈ 5V 时实验波形Fig.8 Experimental waveforms for Vref≈5V

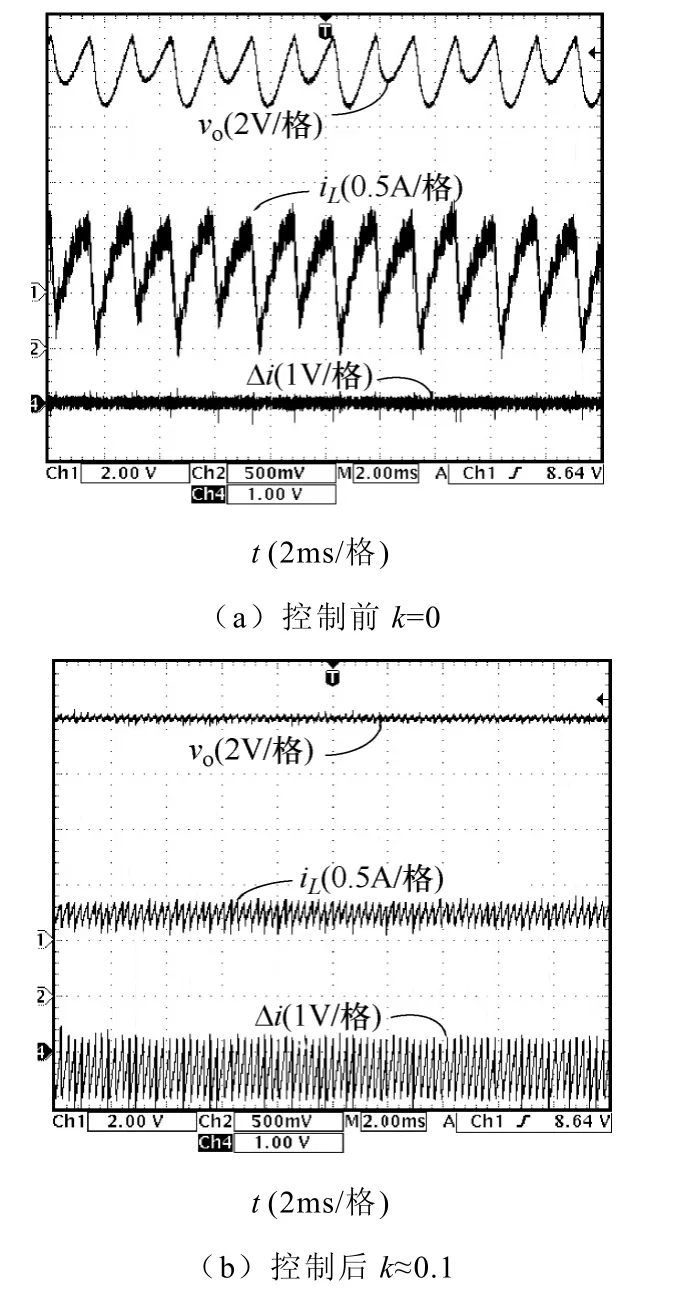
图9 Vref≈ 8V 时实验波形Fig.9 Experimental waveforms for Vref≈8V

6 结论

本文提出了一种零扰动补偿控制新方法，实现了对电流模式Buck 变换器中的不稳定现象的有效抑制，仿真和实验结果验证了理论分析的正确和所提控制思路的有效。此外，所提的扰动控制保留斜坡补偿的优点，其零补偿特性则可避免其现有斜坡补偿的补偿度问题。所提控制电路实现简单，其控制思想同样适用于其他开关功率变换器系统不稳定行为的控制。

[1]Deane J H B.Chaos in a current-mode controlled Boost DC-DC converter[J].IEEE Transactions on Circuits and Systems-I,1992,39(8):680-683.

[2]周宇飞,陈军宁.电流模式控制 Boost 变换器中得切分叉及阵法混沌现象[J].中国电机工程学报,2005,25(1):23-26.Zhou Yufei,Chen Junning.Tangent bifurcation and intermittent chaos in current-mode controlled Boost converter[J].Proceeding of the CSEE,2005,25(1):23-26.

[3]张波.电力电子变换器非线性混沌现象及其应用研究[J].电工技术学报,2005,20(12):1-6.Zhang Bo.Study of nonlinear chaotic phenomena of power converters and their applications[J].Transactions of China Electrotechnical Society,2005,20(12):1-6.

[4]李明,戴栋,马西奎,等.基于改进离散法的含输入滤波器电流型Buck 变换器稳定性分析[J].电工技术学报,2008,23(4):73-80.Li Ming,Dai Dong,Ma Xikui,et al.Stability study on current-mode controlled Buck converter with input filter based on improved discrete approach[J].Transactions of China Electrotechnical Society,2008,23(4):73-80.

[5]Lai Y M,Tse C K,Chow M H L.Control of bifurcation in current-programmed DC/DC converters:an alternative viewpoint of ramp compensation[J].Circuits,Systems and Signal Processing,2001,20(6):695-707.

[6]何亮,方宇,李吉,等.峰值电流控制DC/DC 变换器的恒值限流方法[J].电工技术学报,2006,21(10):86-89.He Liang,Fang Yu,Li Ji,et al.Over current protection for peak current controlled DC/DC converter[J].Transactions of China Electrotechnical Society,2006,21(10):86-89.

[7]包伯成,许建平,刘中.开关DC/DC 变换器斜坡补偿的稳定性控制研究[J].电子科技大学学报,2008,37(3):397-400.Bao Bocheng,Xu Jianping,Liu Zhong.Study on stability control of ramp compensation for switched DC/DC converter[J].Journal of University of Electronic Science and Technology of China,2008,37(3):397-400.

[8]Ye Q,Lai X Q,Li Y M.A piecewise linear slope compensation circuit for DC-DC converters[J].Journal of Semiconductors,2008,29(2):281-287.

[9]Lu J Y,Wu X B.A novel piecewise linear slope compensation circuit in peak current mode control[C].IEEE International Conference on Electron Devices and Solid-State Circuits,2007,12:929-932.

[10]Feng T,Kasemsan S,Batarseh I.An adaptive slope compensation for the single-stage inverter with peak current-mode control[J].IEEE Transactions on Power Electronics,2011,26(10):2857-2862.

[11]周泽坤,王锐,张波.一种自适应斜坡补偿电路[J].电子科技大学学报,2007,36(1):47-49.Zhou Zekun,Wang Rui,Zhang Bo.A self-reacting slope compensation circuit[J].Journal of University of Electronic Science and Technology of China,2007,36(1):47-49.

[12]卢伟国,周雒维,罗全明.反馈稳定控制电路模式DC/DC 变换器[J].电工技术学报,2011,26(3):80-87.Lu Weiguo,Zhou Luowei,Luo Quanming.Feed-back stable control of the current mode DC/DC converters[J].Transactions of China Electrotechnical Society,2011,26(3):80-87.

[13]Aroudi A El,Orabi M.Stabilizing technique for AC-DC Boost PFC converter based on time delay feedback[J].IEEE Transactions on Circuits and Systems-II,2010,57(1):56-60.

[14]Lu W G,Zhou L W,Luo Q M,et al.Filter based non-invasive control of chaos in Buck converter[J].Physics Letters A,2008,372(18):3217-3222.