应用复小波变换检测突发短路时的电力变压器绕组状态

张 坤 王丰华 廖天明 金之俭

（1.上海交通大学电气工程系 上海 200240 2.上海市电力公司技术与发展中心 上海 200025）

1 引言

变压器是电网的重要组成部分，其稳定性和可靠性极大影响着整个电网的安全运行。统计分析表明[1]，相当数量的变压器故障来自于绕组变形。目前常用电量检测法中的频响分析法[2]和短路电抗法[3]等方法对变压器绕组进行检测，这些方法均是建立在变压器绕组的电气模型基础上的，在变压器绕组发生明显变形时能给出较为准确的判断，但在检测变压器绕组松动、扭曲或轻微变形时灵敏度不高。

始于20 世纪80 年代的振动分析法通过检测变压器绕组的机械特性变化反映绕组的状态变化，与传统的电测法相比具有更高的灵敏度[4]，近年来逐步受到国内外研究人员的关注[5,6]。

振动分析法通过测量传递到油箱壁的振动信号来检测变压器的绕组状态，因此，振动信号的分析及绕组状态描述是关键。小波分析具有良好的时频域局部化性能，是分析非平稳信号的有力工具，因而在信号处理中具有广泛的应用。小波分析通常采用实小波基函数，实际上，实值小波只能从幅值的角度提取被分析信号的信息，而复值小波能从幅值与相位两个角度提取被分析信号信息[7]，因此复小波变换具有更高的精度。国内首篇关注复小波的文章出现在1998 年，到目前为止，复小波主要应用在图像处理方面。复小波变换优于实小波之处，除了能额外提供幅值信息、相位信息等简单信息外，还能够提供多种复合信息，并且可以克服实小波平移敏感性、方向性差和无相位信息的缺点。本文重点关注变压器遭受短路冲击时的振动信号特征，通过对复小波算法的研究，使用该算法对实体变压器遭受短路冲击时的振动信号进行分析。依据各频带振动信号和能量，来判断变压器绕组是否存在松动与变形。从而做出实际运行中的变压器遭受短路冲击后，是否需要进一步检修的判断。

2 短路状态下的变压器振动检测法原理

运行中的变压器振动信号主要为铁心振动和绕组振动的叠加。变压器在遭受短路冲击电流时，由于短路电流幅值远远高于额定电流，绕组振动将远大于铁心振动，可认为突发短路时变压器振动主要由绕组振动引起。

文献[8]给出了短路冲击下作用在变压器绕组上的非对称短路电流为

式中，Im为对称短路电流峰值；θ为电源合闸角度；T为短路电流的非周期分量的衰减时间常数。根据洛伦兹定律,可得到短路轴向电动力为

式中，by为幅向漏磁场。

根据变压器绕组的结构特点，视铁心刚度无穷大，压板为刚性，线饼为集中质量且认为每个线饼质量相同，绝缘垫块和上下端圈为弹性元件，各个垫块的弹性系数K和阻尼系数C均相同，则可得变压器绕组的轴向振动系统模型如图1 所示。

图1 绕组轴向振动模型Fig.1 Axial vibration model of power transformer

据此可建立绕组模型动力学运动方程为

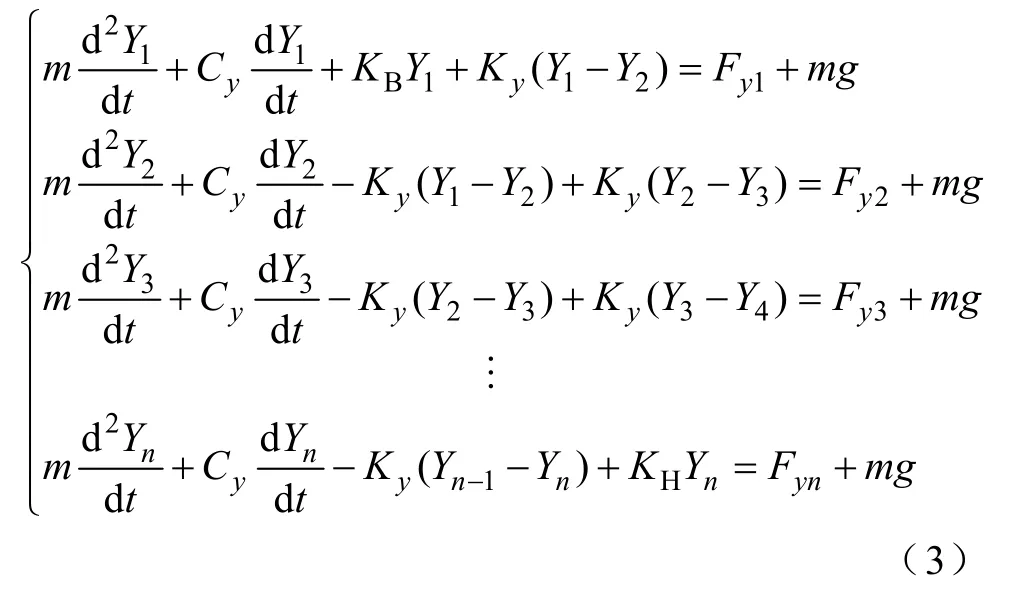
式中，Yn为第n个单元的轴向位移；Cy为阻尼；Ky、KB、KH为刚度系数；m为单个线圈单元的质量。

若近似认为Y1=Y2…=Yn=Y，则可将方程组相加并做如下标记为

则可得到短路动态电动力激励下变压器绕组的轴向振动运动方程为[9]

将式（2）代入式（5）求方程可得到轴向位移Y为

再对Y求两次导即可得到短路冲击下变压器绕组轴向加速度的表达式为

由式（7）可知，变压器承受短路冲击时绕组振动特性与变压器绕组的质量、阻尼、刚度以及短路电流峰值密切相关，所以变压器绕组松动或者变形本质上会影响到变压器绕组的机械动力学特性的变化，从而通过振动信号反映出来。因此，研究突发短路时变压器振动信号的变化特性可以准确判断绕组的振动机械状态。

3 复小波分析算法

小波变换具有良好的时频局部化特性，克服了傅里叶变换及短时傅里叶变换在瞬态信号检测方面的不足，适用于分析暂态、突变信号，因而在非平稳信号处理方面得到了广泛的应用[10]。在小波分析中，通常采用实小波基函数，将信号进行小波分解后作自功率谱、包络谱等分析，很少应用复小波变换进行研究。

3.1 复小波变换的基本原理

设函数ψ(t) 为一平方可积函数，若其傅里叶变换ψ(ω) 满足条件

则称ψ(t) 为一个基本小波。基小波经过伸缩平移得到一系列小波序列

式中，a、b分别为小波函数的尺度因子和位移因子，分别决定小波的时频窗在频域和时域的位置。

对于任意的函数s(t)∈L2(R)，其小波变换及逆变换定义为如下内积

若ψ(t) 为复函数，则为复小波变换。由于ψ(t) 为复函数则变换结果Ws(a,b) 也为复函数，因此复小波变换系数也复数。

3.2 复小波包络提取与时频图分析

由式（10）可得，复小波变换结果为

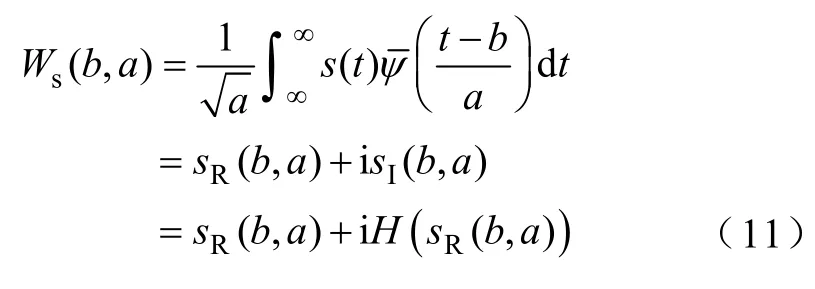
式中，sR(b,a)为小波变换的实部；sI(b,a)为小波变换的虚部；H(sR(b,a))表示sR(b,a)的希尔伯特变换。

经复小波变换后得到的复小波系数维数非常大，如果直接构成分析信号的特征量，势必会出现冗余，不能清晰表征信号信息。由式（11）可知，对信号进行复小波变换后得到的小波系数为解析信号，实部sR(b,a)和虚部sI(b,a)的相位相差90°，满足包络检波技术中的信号解调原理，因此，可以用解调的方法得到小波系数的包络并作为分析信号的特征量为

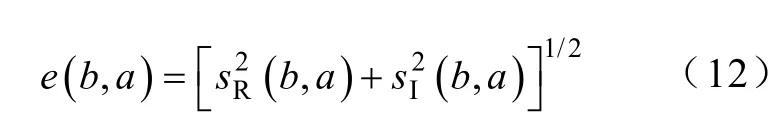
小波时频图是分解结果的直观表示，反映各时刻对应频率的分布和强度。通过小波变换得到小波系数从而提取小波包络，再将尺度转化为频率即可得到三维的频率-时间-小波包络图，即小波时频图。尺度与频率之间的关系为

式中，Fc为小波中心频率；fs为采样频率；a为尺度；Fa为a对应的实际频率。

4 变压器短路冲击试验描述

试验对象为某电力公司一台10kV 电力变压器，在沈阳变压器国家质量检验中心进行短路冲击试验。通过将变压器低压侧引出端使用铜排直接短路，高压侧B 相进行单相26 次短路冲击试验，来检验该变压器在遭受短路冲击时的机械强度。振动信号采集设备采用DH5920 动态信号测试分析仪，传感器为DH185 压电式传感器。图2 为短路冲击试验时加速度传感器的布置位置实物图。

图2 试验变压器及传感器测点布置图Fig.2 Test transformer and the location of probes

振动信号检测系统由3 部分组成，即模拟通道、信号分析仪及总控制台，整体系统框图如图3 所示。模拟通道包括振动传感器、1 394 连接线。实测时，由总控制台控制试验冲击电流，多个吸附于变压器箱体的压电振动传感器获得变压器油箱的振动信号。信号采集后通过DH5902 多功能动态信号分析仪记录后输入计算机中进行分析，据此判断变压器绕组的运行状态。

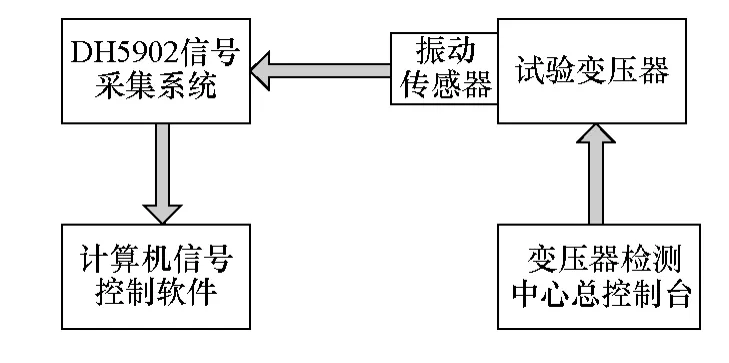
图3 振动信号测试原理图Fig.3 The schematic drawing of vibration test

5 试验结果与分析

图4 为B 相绕组短路冲击的时域波形。由于篇幅所限，本文在此仅列出B 相第17 次、第24 次和第25 次短路冲击时域波形。由图可见，变压器在承受短路冲击时的振动信号是非平稳性信号，并且具有很强的时域特性。随着短路次数及短路电流的增加，B 相短路冲击时域信号的振动幅值呈现递增趋势，B 相第25 次短路冲击时域信号的幅值较前三次有了明显的增加，体现了变压器绕组变形的累积效应。

图4 振动信号时域波形Fig.4 Vibration waveforms under short-circuited impulse

5.1 振动信号时频分布

Morlet 小波是连续小波变换中最常用的一个小波函数，该小波是由高斯函数经余弦复调制而生成，在时域和频域里具有良好的局部化特性[11]，故选择Morlet 小波作为母函数，对变压器振动信号实施复小波变换，得到信号时-频包络图，如图5 所示。

由上图可以看出，在前几次短路冲击中，振动信号以100Hz 为主，高频分量所占比重很小，频谱分布清晰，并且各频率分量幅值随着短路电流的增加而相应变大，400Hz 幅值无明显增加，变压器处于稳定状态；第17 次短路冲击后短路电流大小基本不变，但是振动幅度还是逐次增加，并且频谱分布渐趋杂乱，这个体现了短路电流对绕组机械特性破坏的累积作用；而第25 次短路冲击时，以400Hz 分量为中心的高频分量明显增多，频谱分布杂乱，绕组已经出现了严重的形变，变压器已处于危险期。

表1 给出了几次短路下100Hz 与400Hz 峰值及短路冲击总能量。短路冲击总能量公式为

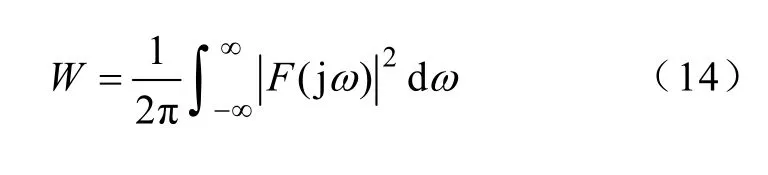
表1 频谱峰值与短路冲击总能量Tab.1 The peak of marginal spectrum and Hilbert energy

由表1 可以发现，第25 次的400Hz 峰值及短路冲击总能量明显增加几倍，说明这是绕组出现了形变，而之前变化率符合正常趋势。

5.2 振动信号分析法与短路电抗法的比较

表2 为相对应的电路冲击后短路电抗以及短路100Hz 分量幅值的变化情况。短路电抗法以短路电抗值为特征量判断变压器绕组状态。由表可见，电抗在第25 次超出了国家标准。由此知，复小波变换的结果与表2 显示的电路电抗法测得结果一致，说明了振动法检测变压器绕组变形的有效性。此外，B 相绕组到第24 次短路冲击电抗偏差仍在1%以内，而振动法100Hz 分量可以很好地反映出绕组逐步松动的迹象，第 25 次短路冲击绕组打坏，振动法100Hz 幅值振幅明显，并且出现一个大量的高频分量，可以敏锐地判别绕组结构发生了明显的变形，可见振动法在判断绕组松动以及变形中具有很高的灵敏度。

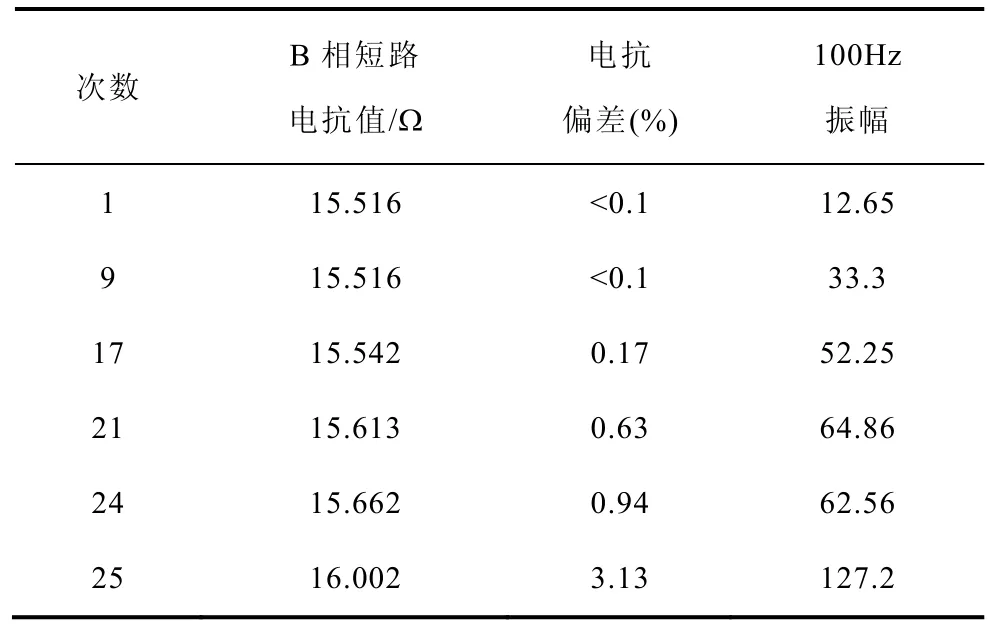
表2 短路电抗值Tab.2 Short circuit reactance

6 结论

本文基于复小波变换法研究了突发短路时变压器实测振动信号的变化特性，据此对变压器的绕组状态进行检测，结果表明：

（1）工频冲击短路电流情况下，振动信号主要集中在二倍频100Hz 处。

（2）复小波时频图能有效反映变压器振动信号频域特性，时频图中100Hz 分量和冲击总能量的大幅增加预示了绕组的松动，而高频分量的出现敏锐地反映出绕组变形的开始。

（3）与常规电抗法检测相比较，用振动分析法能更明确清晰地反映出变压器绕组的故障发展过程与特征。

综上所述，振动法分析变压器绕组松动变形具有很好的灵敏度。结合复小波算法分析，能够准确有效地得到变压器在承受短路冲击下的机械特征信息，从而检测出变压器状态是否良好，并快速做出是否需要检修的判断。这有助于增强变压器运行的稳定性与可靠性，从而更好地保障电网的安全运行。

[1]王梦云.110kV 及以上变压器事故与缺陷统计分析[J].供用电,2007,24(1):1-5.Wang Mengyun.Statistic analysis of transformers faults and defects at voltage 110kV and above[J].Distribution &Utilization,2007,24(1):1-5.

[2]高朝霞,马涛,王永儿,等.短路阻抗法结合频响法诊断变压器绕组变形的分析与应用[J].电力设备,2006,7(12):32-34.Gao Zhaoxia,Ma Tao,Wang Yonger,et a1.Diagnosis of transformer winding deformation by combination of SCR and FRA method[J].Electrical Equipment,2006,7 (12):32-34.

[3]何平,文习山.变压器绕组变形的频率响应分析法综述[J].高电压技术,2006,32(5):37-41.He Ping,Wen Xishan.Survey of frequency response analysis on winding deformation of transformers[J].High Voltage Engineering,2006,32(5):37-41.

[4]Garcia B,Burgos J C,Alonso A M.Transformer tank vibration modeling as a method of detecting winding deformations—part I:theoretical foundation[J].IEEE Transactions on Power Delivery,2006,21(1),157-163.

[5]Garcia B,Burgos,J C,Alonso A M.Transformer tank vibration modeling as a method of detecting winding deformations—part II:experimental verification[J].IEEE Transactions on Power Delivery,2006,21(1),164-169.

[6]傅坚,徐剑,陈柯良,等.基于振动分析法的变压器在线监测[J].华东电力,2009,37(7):1067-1069.Fu Jian,Xu Jian,Chen Keliang,et a1.Online transformer monitoring based on vibration analysis[J].East China Electric Power,2009,37(7):1067-1069.

[7]张大波,刘志刚,张亚军.复小波研究现状及其在电力系统中的应用进展[J].电力系统自动化,2006,30(17):97-104.Zhang Dabo,Liu Zhigang,Zhang Yajun.Complex wavelet transform review and its applications in power system[J].Automation of Electric Power Systems,2006,30(17):97-104.

[8]焦立阳.电力变压器绕组短路电动力的计算[D].沈阳:沈阳工业大学,2009.

[9]谢坡岸.振动分析法在电力变压器绕组状态监测中的应用研究[D].上海:上海交通大学,2008.

[10]杨建国.小波分析及其工程应用[M].北京:机械工业出版社,2005.

[11]何岭松,李巍华.用Morlet 小波进行包络检波分析[J].振动工程学报,2002,15(1):119-122.He Lingsong,Li Weihua.Morlet wavelet and its application in enveloping[J].Journal of Vibration Engineering,2002,15(1):119-122.