一种具有无损钳位电路的三绕组全桥变换器

袁登科 湛凌威 王 兴 张逸成

（同济大学电气工程系 上海 201804）

1 引言

随着社会经济的快速发展，城市的轨道交通系统在世界范围内为缓解城市交通拥堵的压力起到重要作用，目前国内诸如杭州、西安、武汉等二线城市都在大力发展轨道交通。与此同时，轨道交通的安全运营备受瞩目，如北京、上海的轨道交通由于线路众多，电气设备长期重负荷运营，已不可避免出现故障，由于供电网故障中断线路运营的情况屡见不鲜。所以北京地铁4 号线、上海地铁11 号线以及广州地铁某些线路均提出了地铁列车能够在外部电力中断情况下依赖车载蓄电池实施紧急牵引的要求。由于众多地铁列车的供电直流电压为1 500V 系统，而车载蓄电池电压一般均较低，所以采用目前成熟的电力电子变流技术实现电压变换与功率控制是一种理想的解决方案。

然而，在地铁列车长时间需要较大牵引功率时，随着荷电状态的降低，车载储能单元的端电压会在较大范围内变化，所以功率变换器的输入电压变化范围很宽，往往超过两倍的变化范围。对于适于高压与大功率场合的全桥变换器而言，由于变压器漏感和整流二极管结电容的存在，变换器整流二极管在截止的初始阶段往往会承受很高的振荡过电压，尤其是在宽输入电压和高输出电压场合，需要高耐压的二极管。然而随着二极管耐压值的增高，其反向恢复特性变差，这会进一步加剧二极管截止阶段的振荡过程，会使二极管承受更大的电压应力。这个振荡过程不仅对二极管的耐压等级提出了很高的要求，还会导致EMI 问题和更大的器件损耗，包括开关管、变压器和整流二极管。

为了削减高压、大功率全桥变换器中整流二极管电压应力，在近些年来有很多技术被提出。传统的方法采用电容、二极管与电阻构成RCD 钳位电路[2,3]，虽然RCD 钳位电路可以很好地钳位二极管电压应力。然而在大功率宽输入电压Vi场合，电阻上的损耗非常大，因此降低了系统的效率。有源钳位的方法在抑制振荡电压的同时，由于没有电阻，因此损耗很小[4-9]。但由于其采用了开关管，因此增加了系统的控制复杂度，降低了系统的可靠性。所以，在大功率场合，一般不采用此方法[2,3]。为了能在削减损耗的同时降低系统的控制复杂度，一些无损无源钳位电路被提出[10-20]。利用4 个二极管和2个电容构成的钳位电路可以实现无损钳位，但二极管电压应力高达nVi+Vo（Vo为变换器的输出电压，n 为高频变压器二次与一次绕组的匝比），因此对于高电压场合，该拓扑并不合适[13]。文献[14-16]中电路拓扑的钳位电路可以将二极管电压应力钳位到2Vo，在高电压输出时二极管电压应力仍很高。通过带中心抽头的变压器和加入辅助电感，可以将二极管电压应力钳位到1.5Vo[17]，但对于高压输出场合，其电压应力仍然很大，而且加入辅助电感使电路变得更复杂。通过加入辅助电压源将二极管电压应力钳位到Vo/[d+k(1－d)d][18]（k 为绕组匝比系数），该方案在低占空比d 时二极管电压应力仍然很高，同时因采用全波整流方式，并不很适合在高电压输出场合使用。一种简单的钳位电路只利用两个二极管和一个电容可以在高占空比的工况下很好地钳位二极管上过电压[19]，并可以实现开关管的零电流关断。然而对于宽输入电压和高输出电压场合，其二极管电压应力会非常大。因此，在高电压输出场合，很多拓扑采用多绕组全桥变换器并联技术，变换器二次绕组采用串联结构以降低二极管电压应力[20-23]。利用两个二极管和一个电容使二极管电压应力被钳位在输出电压Vo[20]。但由于拓扑本身的限制，电路正常工作时占空比必须大于0.5，因此限制了输入电压的变化范围。文献[23]中电路拓扑的钳位电路在文献[19]的基础上，提出了一种采用此钳位电路的二绕组全桥变换器。此拓扑减小了二极管电压应力，尤其是在高占空比条件下。但在低占空比的情况下二极管电压应力仍然较高。

本文提出了一种新的拓扑结构，此拓扑的变压器二次侧采用三绕组结构，通过对三个绕组的匝比进行优化，使得占空比的工作范围更宽，最低占空比达到0.382，所以变换器可以工作在输入电压变化范围大于二倍的场合；同时电路拓扑使整流二极管电压应力保持在Vo以下。

2 整流二极管电压应力分析

2.1 整流二极管电压应力推导

二极管关断后电压振荡过程在文献[23]中有详细的描述。在考虑二极管反向恢复电流情况下，本节在其基础上进一步推导出整流二极管电压应力最大值的公式，并对此进行详细的分析。全桥变换器原理如图1 所示，S1～S4为一次侧4 个IGBT 开关管，Ls为折算到变压器二次漏感，n 为变压器二次侧与一次侧的匝比，VD1～VD4为二次侧4 个整流二极管，Cj1～Cj4为整流二极管的等效结电容（其电容值记为Cj），Lf为输出滤波电感的电感值，Cf为输出滤波电容器的电容值，RL为等效负载电阻。变压器二次电流为iLs。在二极管电压振荡过程中，由于时间非常短，滤波电感的电流几乎不变，该电流定义为ILf。图1 中Vi为变换器直流输入电压，Vsec为变压器二次电压，Vrec为整流二极管直流侧电压，Vo为变换器输出直流电压。

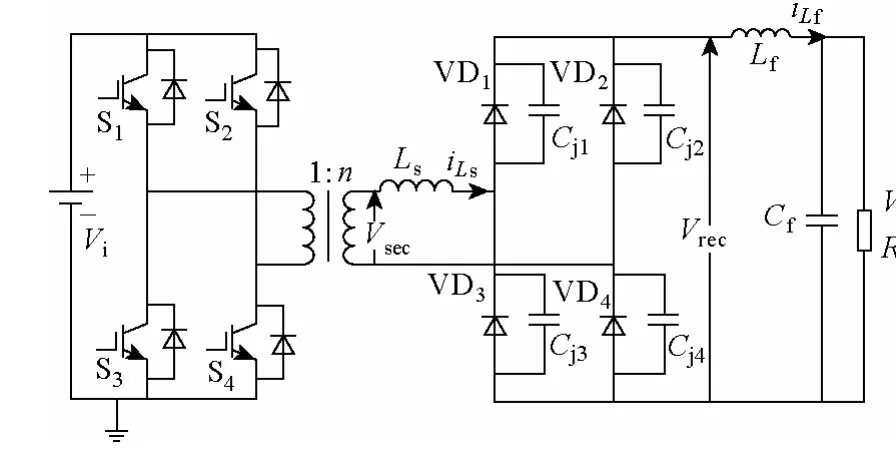
图1 全桥直流变换器原理图Fig.1 Schematic of full bridge converter

以二极管VD2和VD3截止为例。二极管进入电压振荡状态的等效电路如图2 所示，此阶段起始时的漏感电流初始值为 iLs=ILf+2irr（irr为整流二极管的反向恢复电流）。滤波电感可以等效为恒电流源ILf。电容Cj3与Cj2的初始电压为零，初始电流为iCj2=iCj3=irr。因此，漏感和两个结电容构成带初始条件的二阶LC 振荡电路。根据电路基本方程[23]可以得到VD2、VD3的电压应力和变压器二次电流的表达式为

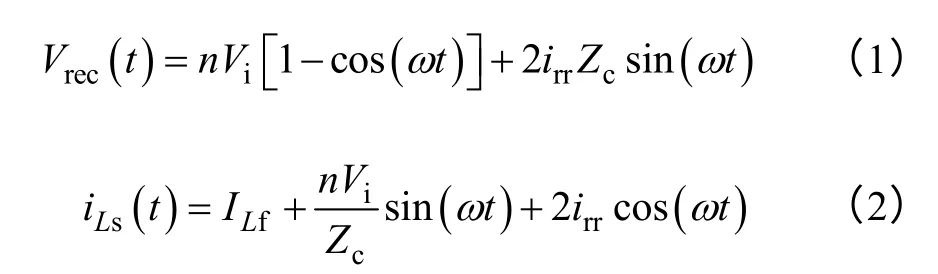
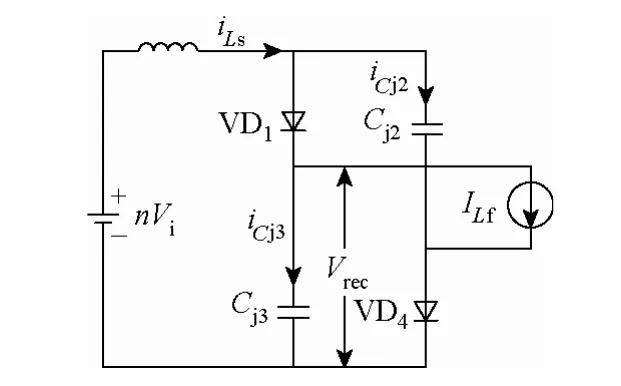
图2 振荡电路等效电路Fig.2 Equivalent circuit of oscillating circuit

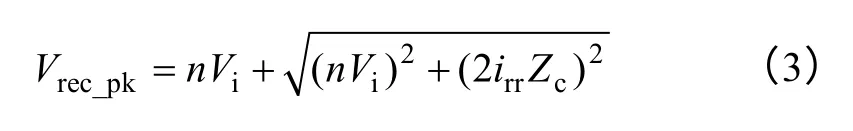
同样，对式（2）求最大值，得到变压器二次电流最大值为

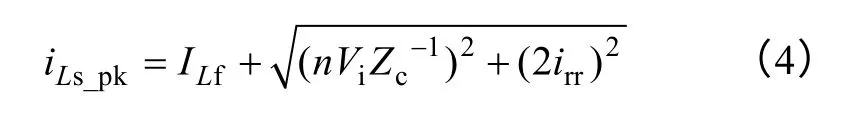
如果整流二极管采用肖特基二极管或者SiC 二极管，其反向恢复电流irr基本可以忽略不计，二极管电压应力最大值为2nVi。而在高压大功率场合，现在的肖特基二极管和SiC 二极管不能满足其电压等级和功率需求，需要采用快恢复二极管，而高压大功率快恢复二极管的反向恢复特性很差，irr很大。根据式（3），二极管的实际电压应力要高于2nVi。在高压大功率场合，二极管电压应力是非常大的，甚至可以达到3nVi[23]。因此，为了能选择开关性能更好、耐压更低的快恢复二极管，对二次整流二极管的振荡电压进行钳位是十分必要的。

2.2 现有典型方案中二极管电压应力的对比分析

下面针对目前相关文献不同方案中，二极管电压应力进行对比分析。以全桥变换器输出直流电压Vo=1 500V、dmin=0.4 为例。

文献[19]方案中二极管电压应力为

实际的电压应力由式（3）和式（5）共同决定，当式（5）的计算值高于式（3）的值时，电压应力由式（3）确定，否则由式（5）确定。

文献[20]方案中二极管电压应力公式如下：

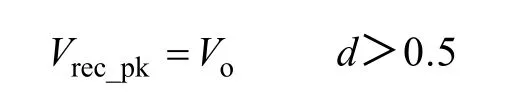
在d ＞0.5 时，二极管电压应力被钳位在输出电压，即Vrec_pk=1 500V，然而此拓扑结构无法在d＜0.5 的情况下工作。

文献[23]方案中的二极管电压应力公式如下：

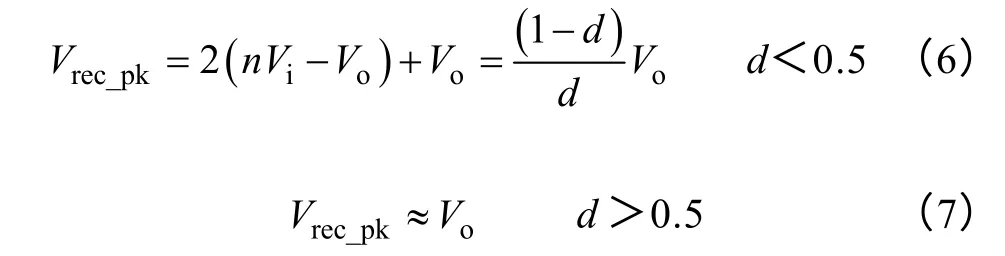
其电压应力为

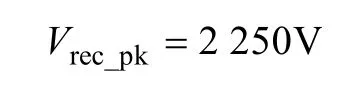
文献[23]的电路拓扑结构在文献[19]的电路拓扑结构的基础上，进一步减小了二极管电压应力。但在d=0.4 时，理论上的二极管电压应力仍然高达2 250V。实际上考虑到二极管的反向恢复电流，二极管电压应力要高于2 250V。

综上所述，文献[19,23]的无损钳位电路在宽输入电压情况下二极管电压应力很大，文献[20]的无损钳位电路无法实现在d＜0.5 的情况下工作。因此，需要新的拓扑结构来实现更宽的输入电压，同时需有效钳位二极管电压应力。

3 具有无损钳位电路的三绕组全桥变换器

3.1 工作原理

本文提出的三绕组全桥变换器如图3 所示，它由三组二次侧采用串联结构的全桥变换器和无损钳位电路构成。无损钳位电路由三个钳位二极管VDc1～VDc3和两个高频滤波电容Cc1和Cc2构成，其工作原理如下。

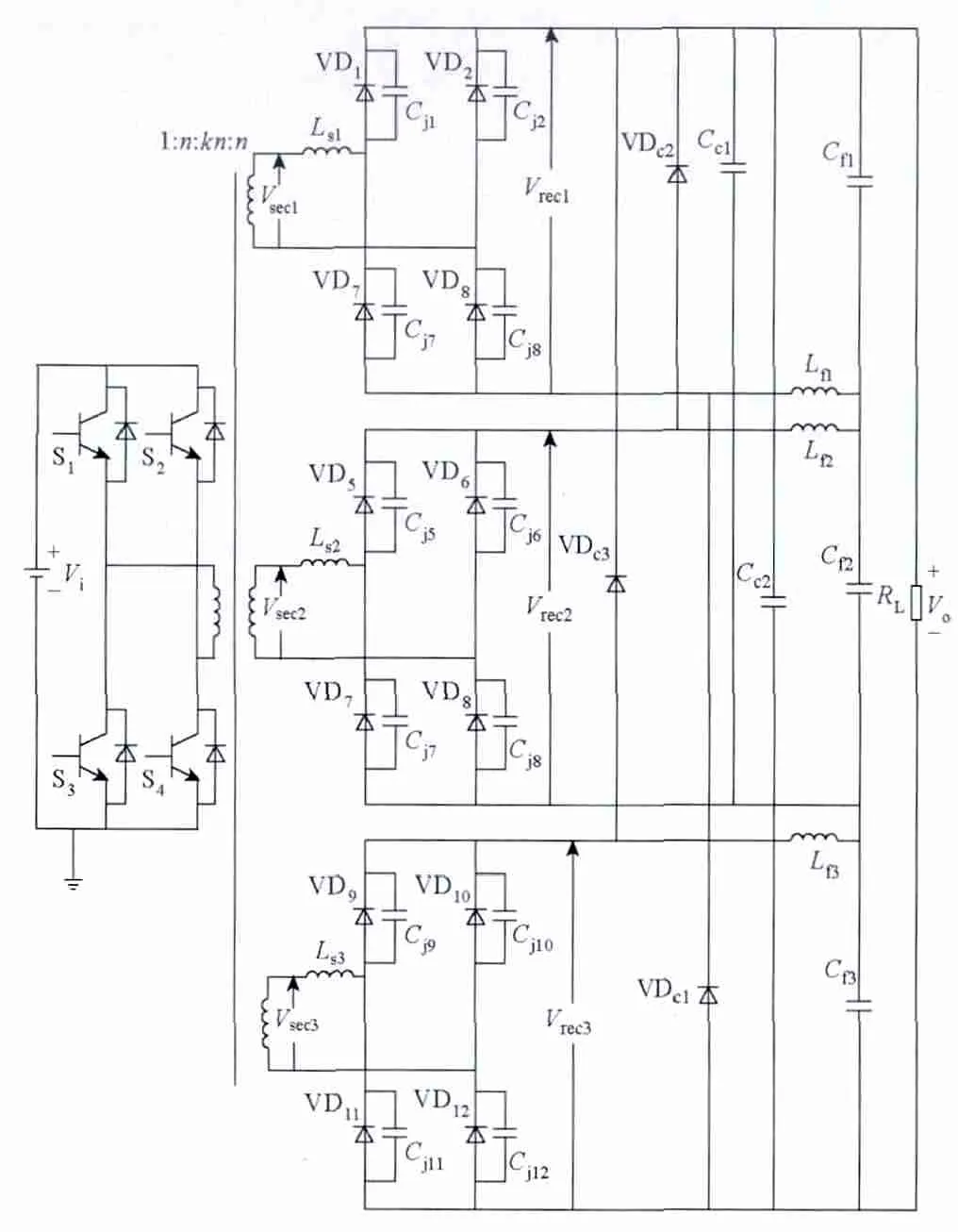
图3 具有无损钳位电路的三绕组全桥变换器Fig.3 Three windings full bridge converter with a lossless clamp circuit

第一组整流二极管：当VD1、VD4（或者VD2、VD3）导通输出电压 Vrec1达到电容 Cc2的电压(VCc2=Vo)时，VDc1导通，因此第一组整流二极管电压应力被钳位在 Vo。振荡电路所产生的能量通过VDc1传递到Cc2中，当振荡过程结束后，Cc2的能量再传递到负载。

第二组整流二极管：当VD5、VD8（或者VD6、VD7）导通后的整流输出电压Vrec2达到电容Cc1的电压(VCc1=VCf1+VCf2)时，VDc2导通，二极管电压应力被钳位在电压(VCf1+VCf2)，振荡电路所产生的能量通过VDc2传送到Cc1中，当振荡过程结束后，Cc1的能量传到负载。

第三组整流二极管：第三组整流二极管的钳位过程与第一组类似。二极管电压应力由VDc3和Cc2钳位，使电压应力被钳位在Vo。

3.2 三绕组变压器匝比优化

图3 所示的变换器二次侧采用了三绕组结构，如果三组绕组的匝比相同，那么变换器无法工作在d＜0.5 的情况下，原因如下：假设高频变压器一、二次侧三个绕组的匝比为1:n:n:n，则Vrec1=Vrec2=Vrec3=nVi，Vo=(Vrec1+Vrec2+Vrec3)d。

为了防止钳位电路的二极管在能量传递时恒导通导致滤波电感短路，需要满足以下三个公式：

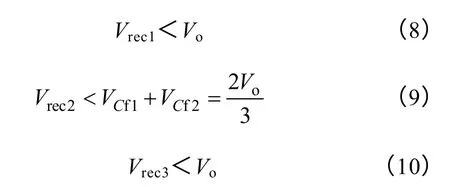
由式（8）和式（10）可以得到 d＞1/3，由式（9）可以得到d＞0.5。因此，变换器允许的最低占空比是0.5，无法实现更宽的输入电压范围。

为了实现更宽的输入电压变化范围，可以考虑具有不同匝比的三绕组结构，假设变压器的匝比为1:n:kn:n，故有

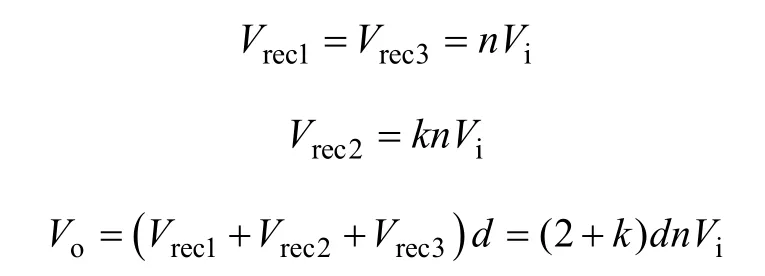
同样，为防止钳位二极管在能量传递时恒导通导致滤波电感短路，需要满足以下三个公式：

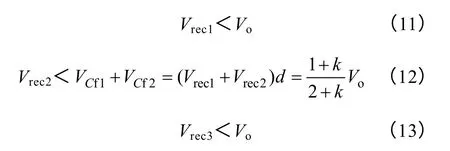
由此可以得到

只有当d 同时满足以上式（14）与式（15）时，电路才可以正常工作。函数f1(k)=1/(2+k)和f2(k)=k/(1+k)的曲线如图4a 所示。当二条曲线相交时，可以取得最小的占空比dmin。此时≈0.618，dmin/(2+k)≈0.382。

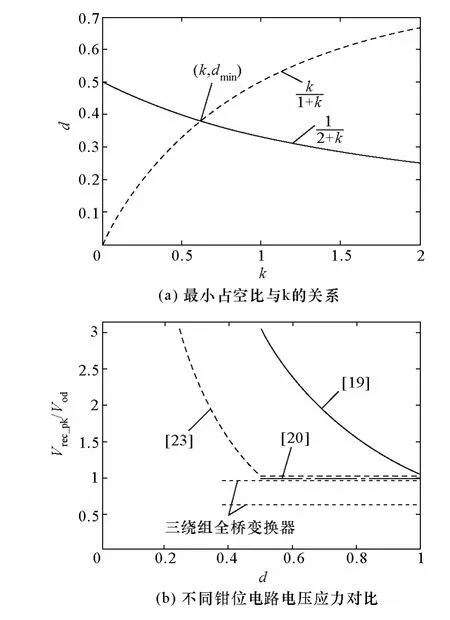
图4 电压应力与占空比关系Fig.4 Relationship between voltage stress and duty ratio

理论分析表明，当变压器的匝比为1:n:0.618n:n时，电路工作时最低占空比可以达到0.382，相比之前最低占空比 0.5，可以使输入电压的工作范围更宽。图4b 给出了文献[19,20,23]和本文提出的具有上述匝比的变换器整流二极管电压应力对比曲线及占空比工作范围，其中横坐标为 d，纵坐标为Vrec_pk/Vo。从图4b 中可以看出，在d＞0.5 时，文献[19]中的二极管电压应力最大，文献[20,23]和本文提出的钳位电路可以使二极管电压应力钳位在Vo。当d＜0.5 时，文献[19,23]中的电压应力增加，文献[20]中的钳位电路不能工作。本文提出三绕组变换器可以使占空比最低为0.382，并钳位二极管电压应力，其中第一组和第三组整流二极管电压应力为Vo，第二组整流二极管电压应力为0.618Vo。

3.3 滤波电感参数优化

由于采用不同匝比的三绕组结构，因此第二组整流桥经过滤波后的输出电压VCf2与VCf1、VCf3不同，即VCf2=kVCf1=kVCf3。由于三组整流桥的输出采用串联结构，因此要求每组整流桥后的滤波电感的纹波电流大小一致，否则不同的纹波电流将流过滤波电容，造成大的纹波电压和发热损耗。以续流阶段为例，纹波电流的变化率为

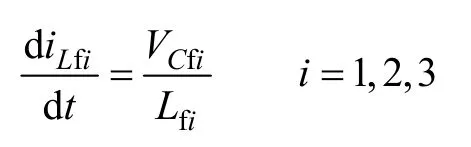
为了使每组的滤波电感纹波电流一致，根据VCf2=kVCf1=kVCf3，则Lf2=kLf1=kLf3。由此可见，为了防止大电流流过滤波电容，每组整流桥的滤波电感的电感量也要进行合理的设计。

4 实验结果

课题组研制了300W 实验样机，以验证三绕组全桥变换器可以在低占空(d＜0.5) 的工况下工作而不发生短路，同时对采用无损钳位电路和不采用钳位电路的三绕组全桥变换器的性能进行了对比实验。实验电路的参数见表1。

实验结果如图5 所示。图5a～图5f 为d=0.4 时整流二极管电压应力曲线。图5a 和图5b 为第一组整流二极管电压应力曲线。可见，加钳位电路的整流二极管电压应力被钳位在输出电压，未加钳位电路的整流二极管电压应力远高于输出电压。图 5c和图5d 为第二组整流二极管电压应力曲线。加钳位电路的电路拓扑中，整流二极管电压应力被钳位在第一组和第二组滤波电容串联后的电压VCf1+VCf2。未加钳位时，整流二极管电压应力远高于第一组和第二组滤波电容串联后的电压VCf1+VCf2。图5e 和图5f 为第三组整流二极管电压应力曲线。加钳位电路的整流二极管电压应力被钳位在第二组和第三组滤波电容串联后的电压VCf2+VCf3。未加钳位时，整流二极管电压应力远高于第二组和第三组滤波电容串联后的电压VCf2+VCf3。图5g～图5i 为高占空比时加钳位电路时整流二极管电压应力曲线，电压应力均被钳位在对应的电压水平。图6 给出了试验平台的布置。

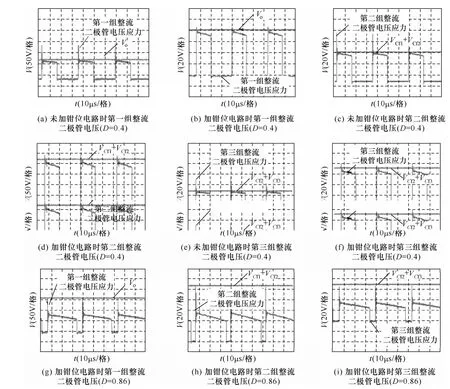
图5 整流二极管电压应力波形Fig.5Waveforms of the rectifier diodes voltage stress

图6 试验平台Fig.6 Experimental platform

5 仿真及实验验证

为进一步验证三绕组变换器在大功率变换器上应用的可能性，通过PSPICE 对大功率变换器进行了仿真分析，得到了初步的验证。

PSPICE 中详细的仿真参数设置见表2。仿真结果如图7 和图8 所示。其中图7 表示第一组整流二极管的电压和输出电压之间的关系，可以看出，二极管电压应力被钳位在输出电压1 500V；图8 表示第二组整流二极管电压应力，可以看出，二极管电压应力被钳位在930V。第三组整流二极管电压应力波形与第一组类似。从仿真结果可以明显看出整流二极管电压应力的钳位效果与前面的试验相似，所以初步验证了本文提出的三绕组全桥变换器在大功率场合应用的可能性。

表2 PSPICE 仿真参数Tab.2 Parameters of PSPICE simulation

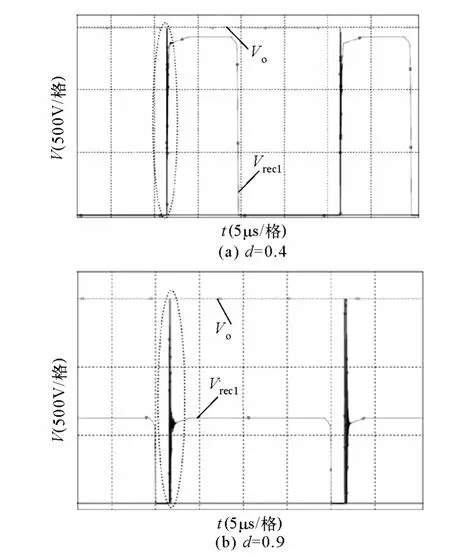
图7 第一组整流桥波形Fig.7Waveforms of the first rectifier bridge

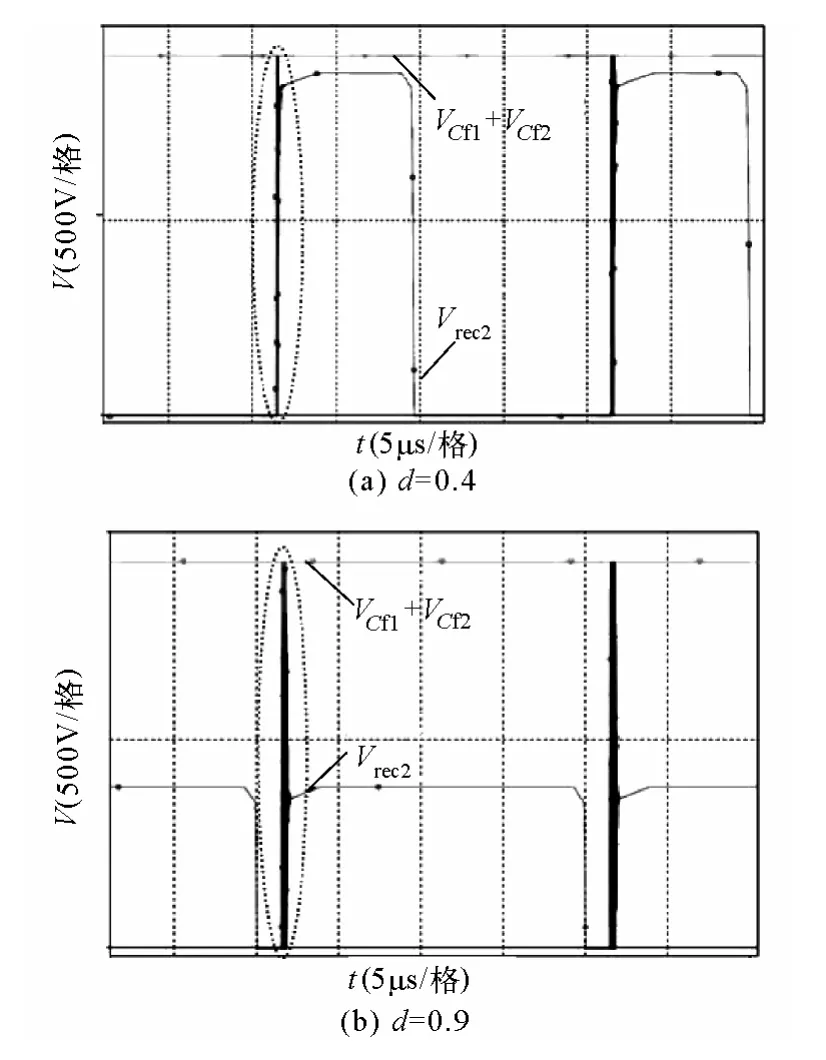
图8 第二组整流桥波形Fig.8Waveforms of the second rectifier bridge

6 结论

本文针对宽输入电压、高输出电压的大功率直流变换的需求，提出了一种具有无损钳位电路的三绕组全桥变换器，详细分析了整流二极管电压应力及其钳位电路，通过对变换器二次三个绕组的匝比进行优化设计，可以拓宽变换器的占空比工作范围，从而使得变换器适用于工作在输入电压变化范围大于2 倍的高压大功率应用场合。小功率试验样机初步验证了提出的具有无损钳位电路的三绕组变换器的有效性，PSPICE 的仿真结果也初步验证了该变换器在大功率场合应用的可能性。

[1]Sabate J A,Vlatkovic V,Ridley R B,et al.Design considerations for high-voltage high-power fullbridge zero voltage-switched PWM converter[C].IEEE Applied Power Electronics Conference,1990:275-284.

[2]Mweene L H,Wright C A,Schlecht M F.A 1 kW 500 kHz front-end converter for a distributed power supply system[J].IEEE Transactions on Power Electronics,1991,6(3):398-407.

[3]Lin S,Chen C.Analysis and design for RCD clamped snubber used in output rectifier of phase-shift full bridge-bridge ZVS converters[J].IEEE Transactions on Industrial Electronics,1998,45(2):358–359.

[4]Sabate J A,Vlatkovic V,Ridley R B,et al.Highvoltage,high-power,ZVS,full-bridge PWM converter employing an active snubber[C].IEEE Applied Power Electronics Conference,1991:158-163.

[5]Cho J G,Rim G H,Lee F C.Zero voltage and zero current switching full bridge PWM converter using secondary active clamp[C].IEEE Power Electronics Specialist Conference,1996:657-663.

[6]Dudrik J,Spánik P,Trip N D.Zero-voltage and zero-current switching full-bridge DC-DC converter with auxiliary transformer[J].IEEE Transactions on Power Electronics,2006,21(5):1328-1335.

[7]Chen T F,Cheng S.A novel zero-voltage zero-current switching full-bridge PWM converter using improved secondary active clamp[C].IEEE International Symposium on Industrial Electronics,2006:1683-1687.

[8]孙铁成,郭建辉,王宏佳,等.改进型具有电压钳位的全桥ZVZCS PWM DC/DC 变换器.电工技术学报,2007,22(7):47-51.Sun T C,Guo J H,Wang H J,et al.Improved full-bridge ZVZCS PWM DC/DC converter using voltage clamping[J].Transactions of China Electrotechnical Society,2007,22(7):47-51.

[9]Dudrik J,Spánik P,Trip N D.Soft-Switching PS-PWM DC–DC converter for full-load range applications[J].IEEE Transactions on Power Electronics,2010,57(8):2807-2814.

[10]Kim E S,Joe K Y,Kye M H,et al.An improved soft switching PWM FB DC/DC converter for reducing conduction losses[J].IEEE Transactions on Power Electronics,1999,14(2):258-264.

[11]Park K B,Kim C E,Moon G W,et al.Voltage oscillation reduction techniques for phase-shift fullbridge converter[J].IEEE Transactions on Industrial Electronics,2007,54(5):2779-2790.

[12]陈武,阮新波,张容荣.加复位绕组的零电压开关PWM 全桥变换器[J].电工技术学报,2007,22(11):117-124.Chen Wu,Ruan X B,Zhang R R.ZVS PWM full-bridge converter with reset winding[J],Transactions of China Electrotechnical Society,2007,22(11):117-124.

[13]孙铁成,王宏佳,张学广,等.一种采用无源箝位电路的新型零电压零电流开关变换器[J].中国电机工程学报,2006,26(17):72-76.Sun T C,Wang H J,Zhang X G,et al.A novel ZVZCS converter using passive clamp circuit[J],Proceedings of the CSEE,2006,26(17):72-76

[14]Ting S T,Nianci H.A novel zero voltage and zero current switching full bridge PWM converter[C].IEEE Applied Power Electronics Conference,2003:1088-1092.

[15]Song T T,Huang N.A novel zero-voltage and zero current switching full-bridge PWM converter[J].IEEE Transactions on Power Electronics,2005,20(2):286-291.

[16]Song T T,Huang N C,Ioinovici A.A family of zero-voltage and zero-current-switching three-level DC-DC converters with secondary-assisted regenerative passive snubber[J].IEEE Transactions on Circuits and Systems,2005,52(11):2473-2481.

[17]Wu X,Xie X,Zhang J,et al.Soft switched full bridge DC-DC converter with reduced circulating loss and filter requirement[J].IEEE Transactions on Power Electronics,2007,22(5):1949-1955.

[18]Wu X,Xie X,Zhao C,et al.Low voltage and current stress ZVZCS full bridge DC-DC converter using center tapped rectifier reset[J].IEEE Transactions on Industrial Electronics,2008,55(3):1470-1477.

[19]Cho J G,Baek J W,Jeong C Y,et al.Novel zero-voltage and zero-current-switching full-bridge PWM converter using a simple auxiliary circuit[J].IEEE Transactions on Industrial Applications,1999,35(1):15-20.

[20]Bendre A,Norris S,Divan D,et al.New high power DC-DC converter with loss limited switching and lossless secondary clamp[J].IEEE Transactions on Power Electronics,2003,18(4):1020-1027.

[21]Bendre A,Wallace I,Luckjiff G A,et al.Design considerations for a soft-switched modular 2.4-MVA medium-voltage drive[J].IEEE Transactions on Power Electronics,2002,38(5):1400-1411.

[22]Bendre A,Venkataramanan G,Divan D.Dynamic analysis of loss-limited switching full-bridge DC-DC converter with multimodal control[J].IEEE Transactions on Power Electronics,2003,39(3):854-863.

[23]Cha H Y,Chen L H,Ding R J,et al.An alternative energy recovery clamp circuit for full-bridge PWM converters with wide ranges of input voltage[J].IEEE Transactions on Power Electronics,2008,23(6):2828-2837.