特殊情况下输电线路的悬高测量
2014-11-24
(丽水职业技术学院 浙江丽水 323000)
全站仪内置程序悬高测量因反射棱镜必须安置在目标点的垂直投影处,在实际操作中受到较大制约。针对跨河输电线悬高测量因其既无法安置棱镜,目标点也不明确,有时还需同时求出目标点三维坐标等特殊情况,一些测量工作者对其进行了探讨[1]—[5],如文献[1]林华等提出利用塔间输电线的垂直投影是一条直线的特点,如图1,通过正弦定理计算△ABC的水平夹角β1,然后根据全站仪测得的水平角β2计算出测站点C 至目标点P的水平距离DCP,再结合目标点的竖直角α 和仪高i,通过EXCEL 内业数据处理,快速解求目标点P 三维坐标的方法(以下简称正弦法)。该法当β1≈90°时易出现因角值判断失误而出错。为此,笔者提出用余弦定理(以下简称余弦法)和坐标反算(以下简称坐标反算法)求解β1 两种新思路,用AutoCAD 和计算器编程现场进行内业数据快速处理两种新方法,并对目标点悬高高程中误差的影响因素进行分析。
1 输电线路悬高测量思路
如图1,正常情况下,两座高压铁塔之间处于悬垂状态的某根高压线,其线型在水平面上的投影可以看做一条直线。首先运用前方交会等方法测定悬线上A、B点的坐标值,A、B点可选择悬线上的端点或者明显特征点;然后在与A 或B点通视的已知点C 架设全站仪,量出仪高,测出直线CA 与直线CP的半测回水平夹角β2,高压线底部目标点P点的半测回竖直角α。
因A、B、C 三点坐标已知,故根据坐标反算可得直线CA、直线AB 和直线BC的水平距离DCA、DAB和DBC,如DCA的计算公式为∶
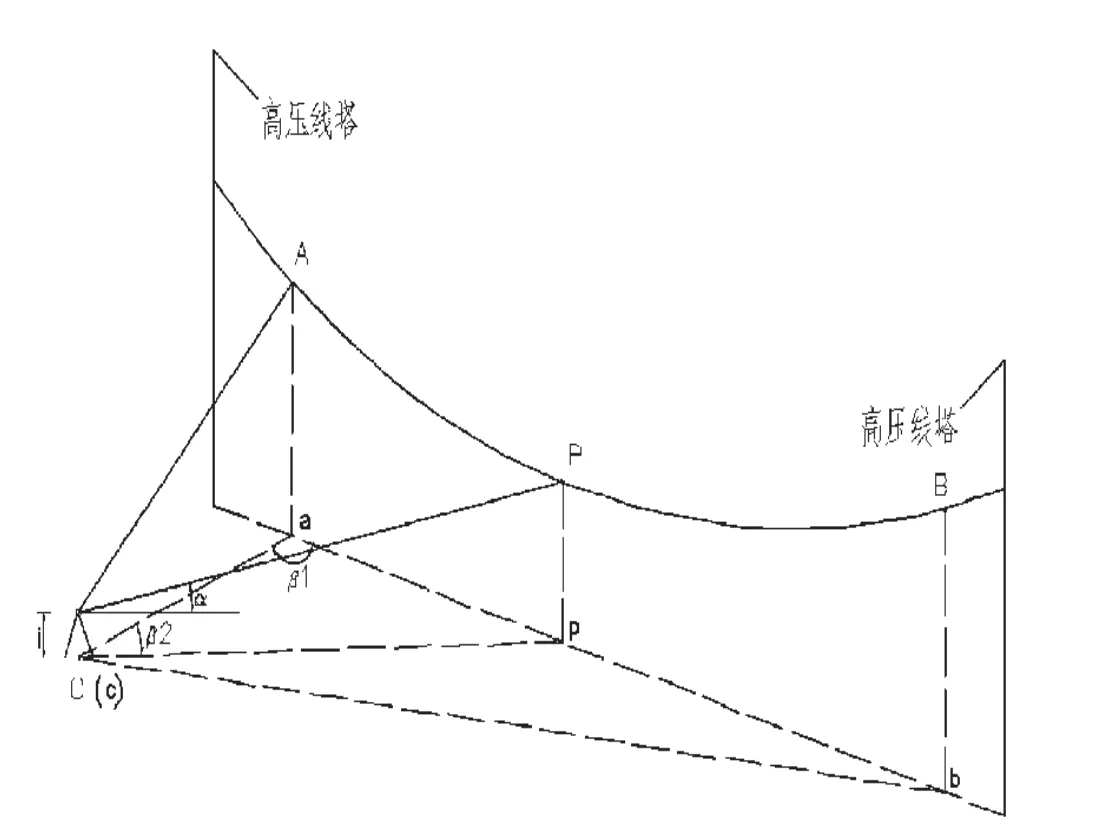
图1
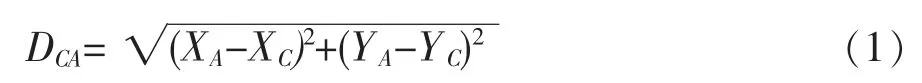
同样因A、B、C 三点坐标已知,故直线CA 与直线AB的水平夹角β1可求得∶
方法一∶余弦法
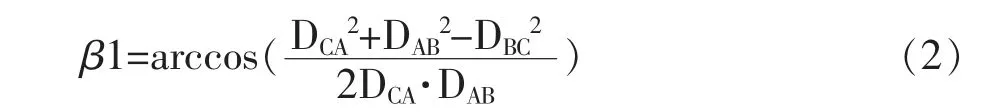
方法二∶坐标反算法

式中,αAC、αAB为根据A、B、C 三点平面坐标反算出来的直线AC、AB的方位角
根据β1 和全站仪实测的直线CA 与直线CP的半测回水平夹角β2,可求得水平距离DCP∶
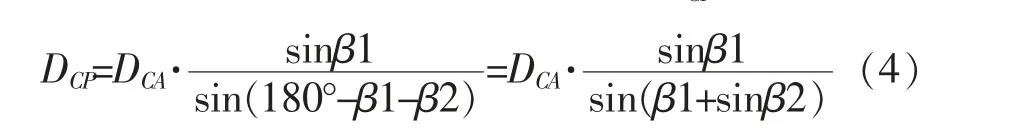
根据C点的高程HC、仪高i、β1、β2、和高压线底部目标点P的半测回竖直角α,可求得目标点P的高程HP∶
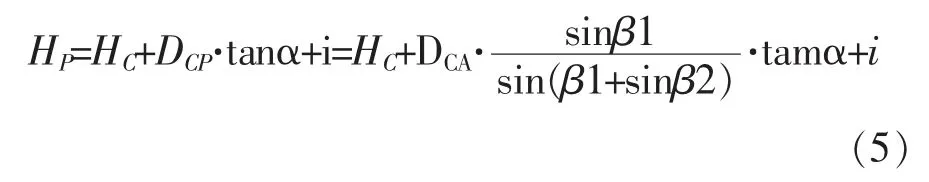
根 据C点的平面坐标XC、YC,DCP,LA的方位角αCA、β2,可求得目标点P的平面坐标∶
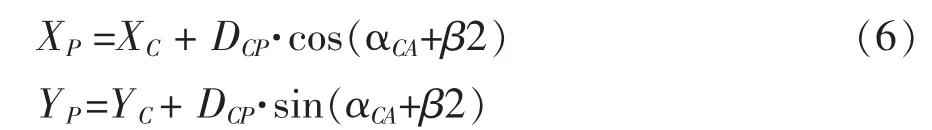
2 悬高测量内业快速解算方法
根据上述计算公式可采用普通计算器逐步计算。但因所涉及的公式较多(获得A、B 特征点的平面坐标还用到了前方交会公式),既费时又容易出错。AutoCAD 有着全面、快速、精确的绘图及查询功能,操作也较简单,故实际工作中可采用AutoCAD软件现场快速绘制并查询A、B、C、P点平面坐标和水平距离DCP。另外用编程计算器编程也可达到现场快速解算的目的。
3 目标点P 高程误差分析
利用全站仪对输电线路进行悬高测量,涉及到的误差较多,为便于讨论,此处暂不考虑测站点C的高程误差、CA的距离误差和水平角β1的角度误差。现对(5)式进行全微分。
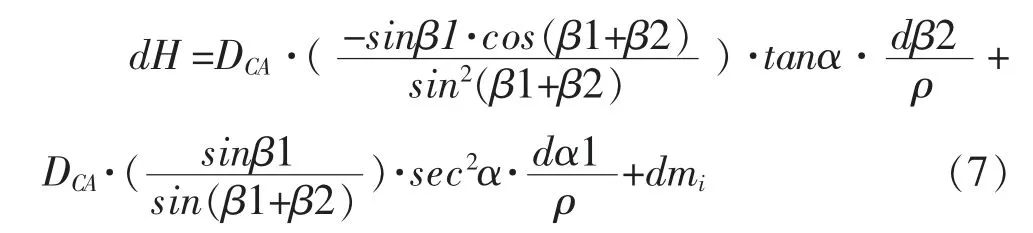
根据(7)式可得HP的中误差平方公式,即
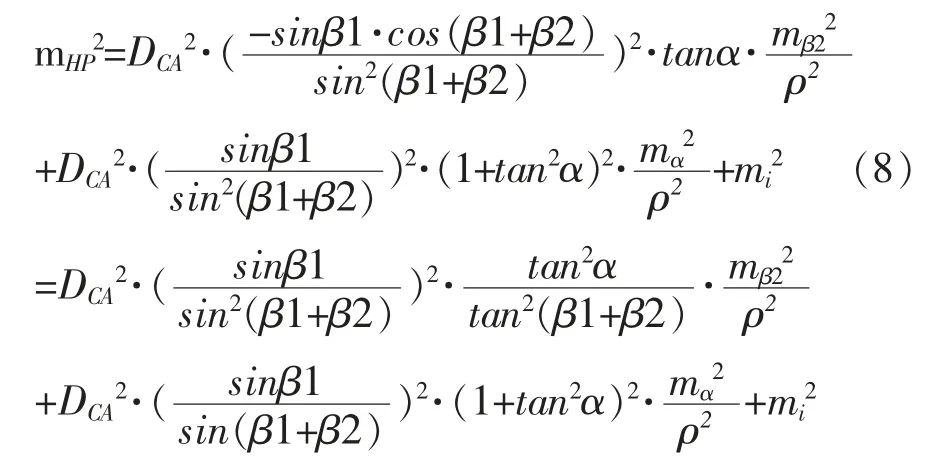
(8)式表明∶悬高测量的中误差mHP不仅与水平角观测中误差mβ2、竖直角观测中误差mα和仪高的中误差mi有关,而且还与DCA、β1、β2 和α的大小有关,当β1、β2 一定时,mHP随DCA、α、mi、mβ2和mα的增大而增大。由于测量目标点处于悬空状态(如220kV 输电线一般离地面7m 以上,500kV 输电线一般离地面14m 以上)[3],跨河输电线路,输电线距离河面最大值在40m 左右,所以误差分析时可取DCA=0.5km,竖直角α=5°,若实际测量时选用2秒的全站仪,则可取mβ2=8″,mα=15″,mi=2mm,则mHP只与β1、β2的大小有关,具体见表1。

表1 β1、β2 改变时悬高点P的高程中误差
从表1不难看出∶ 当DCA、α、mi、mβ2和mα一定时,水平角β1、β2的大小对悬高点P的高程中误差mHP影响较大,且都随β1、β2 角值的增大而增大。实际测量时,应控制β1<90°。
4 结语
本文对文献[1]介绍的方法在内业计算公式上进行了进一步的改进,结果表明,该方法能较好的解决跨河等输电线悬高测量中既无法安置棱镜,目标点也不明确,有时还需同时求出目标点三维坐标等特殊情况,并且很容易测出两塔间输电线路上的任意点,坐标较准确地绘制既有输电线路立面图,该方法也可用在既有拱桥拱圈线形测量项目上。实际测量时,根据所需的精度合理选择全站仪以控制角度中误差,合理选择测站以控制竖直角和相关水平距离以及相关水平角的大小,这是保证测量结果精度的关键所在。
[1]林华,邓建,赵福先.输电线路悬高测量方法新探[J].江西测绘,2010,(2).
[2]余祖锋.架空高压线悬高测量及线型拟合方法[J].中国市政工程,2013,(2).
[3]魏利国,张勇.输电线路悬高测量方法探讨[J].制冷空调与电力机械,2007,(4).
[4]刘启寿,魏兰花.坐标转换在悬高测量中的应用[J].西北水电,2012,(1).
