总体最小二乘的改进与信道估计应用＊

（海军驻上海地区电子设备军事代表室 上海 200233）

1 引言

早在1795年，高斯就提出了最小二乘（Least Squares，LS）法，应用于行星和彗星运动轨道的计算。LS法用于超定方程的参数估计，使得观测值与计算值之间的误差在均方意义上最小：

式中A为已知的数据矩阵，y为观测值，h为待估计的系数。此后最小二乘法被用来解决许多实际问题，针对不同用途，对最小二乘法进行修正，产生了各种各样的最小二乘算法。普通最小二乘（Ordinary Least Squares，OLS）问题中，假定误差只存在于观测值中

其中r为y的误差，OLS问题的解xOLS使得r的L2范数最小。1980年Golub等［1］提出总体最小二乘（Total Least Squares，TLS）的概念，总体最小二乘问题与OLS问题不同，TLS问题中假定误差不只存在于观测值中，而且存在于数据矩阵中

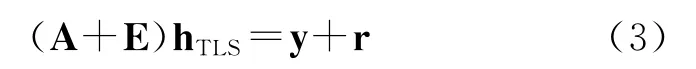
其中E和r分别为A 和y的误差。TLS问题的解xTLS使得［E b］的l2范数最小。一般的估计问题中TLS法可以得到比LS法更加合理的结果。R．D．Degroat等［2］提出在信道均衡中，误差只存在于数据矩阵中，提出了数据最小二乘（Data Least Squares，DLS）：

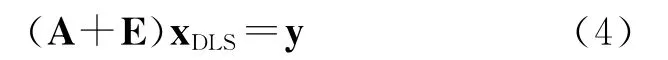
DLS问题的解xDLS使得E 的L2范数最小，DLS在FIR 信道均衡中性能优于TLS。但是在具有误差先验知识的情况中，OLS，DLS，TLS都无法限定误差的特性，不能充分利用系统的先验知识，因此无法获得最优解。约束总体最小二乘（Constrained Total Least Squares，CTLS）［3］和结构总体最小二乘（Structured Total Least Squares，STLS）分别限定了误差矩阵［E b］的统计特性和结构特性，适用于具有一定误差先验知识的系统参数估计问题。文献［4］指出CTLS和STLS得到的解是等价的。本文介绍一种STLS 算法—结构总体最小范数（Structured Least Squares Norm，STLS）［5～7］，解决具有Toeplitz结构误差矩阵的参数估计问题，并将该算法应用于叠加训练序列（Superimposed Training，ST）［8～11］信道估计中。

本文所用的标记说明：大写（小写）粗体字母代表矩阵（列向量），上标T代表转置运算，上标H代表共轭转置，上标†代表伪逆运算，⊗代表Kronecker积，δ（τ）代表Kronnecker函数。IN代表N×N维单位矩阵，IK代表K×1维矢量。

2 STLN 算法

针对式（3）的TLS 问题，已知误差矩阵E 为Toeplitz矩阵。设α为E的第1列，若α或E中任意一个已知，则可求出另一个的值。剩余矢量β＝y-（A＋E）h为α，h的函数，即β＝β（α，h）。STLN问题可写为

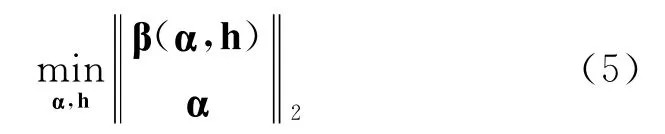
矢量Eh 必须写成包含α 的形式。定义矩阵H，使得

因此H的第1列为［h（0）h（1） …h（L-1） 0 … 0］T且

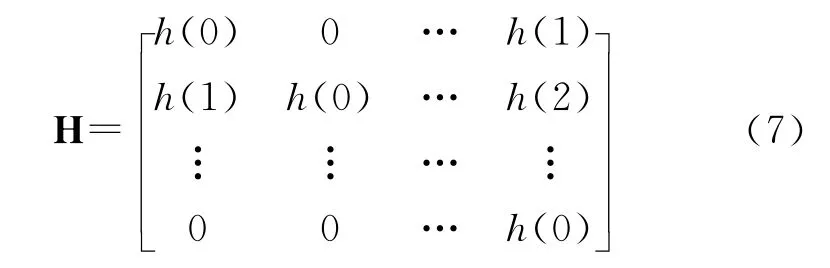
令Δα为α的扰动，Δh对应于h中的扰动。根据式（6）有

忽略下式中Δα和Δh的二阶以上统计量

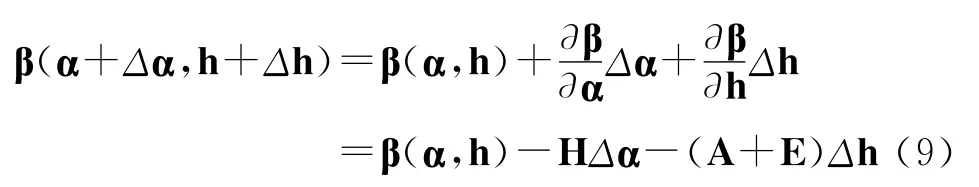
表达式（5）的线性表达式为

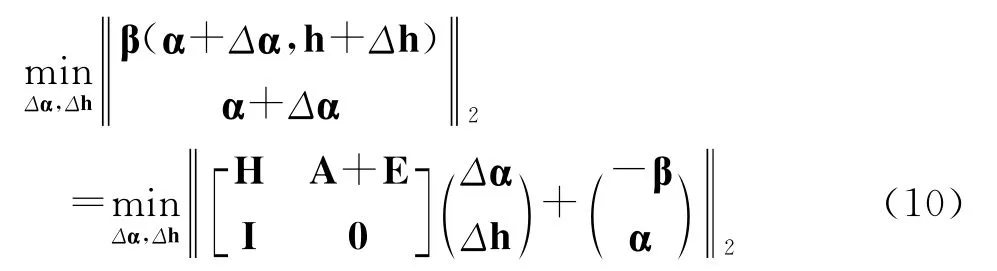
STLN 算法总结如下［5］：

输入：确定性矩阵A，矢量y，初始估计值h，容错值ε。

输出：Toeplitz结构的误差矩阵E，信道冲击响应估计值h，STLN 问题的误差‖βT，αT‖2。

开始

1．令α＝0，则E＝0。令误差向量β＝y-（A＋E）h。

2．重复

（b）令α∶＝α＋Δα，h∶＝h＋Δh

（c）通过α重构E，由h重构H。计算β＝y-（A＋E）h。

直到 （‖Δα‖2，‖Δh‖2≤ε）

结束

解超定方程

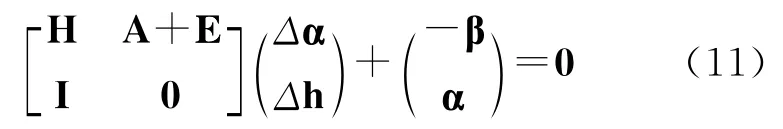
式（11）的OLS解

事实上不需要重复步骤2直到‖Δα‖2，‖Δh‖2≤ε，重复两到三次一般就可以得到足够精确的估计值。

3 基于STLN 算法的叠加训练序列信道估计

3．1 叠加训练序列系统模型

无线通信系统中，通常采用训练序列进行信道估计。传统的时分复用训练序列降低了带宽利用率。叠加训练序列中，周期训练序列与信息序列相加后发送，从而节约了宝贵的带宽资源，但是却降低了发送端的信噪比。在叠加训练序列信道估计中信息序列作为干扰严重降低了信道估计性能，在仿真中增大了归一化信道均方误差（Normalized Channel Mean Squares Error，NCMSE）。本节将推导叠加训练序列频率选择性信道估计中误差（干扰）矩阵的Toeplitz结构。

图1为单输入单输出（Single-Input Single-Output，SISO）叠加训练序列通信链路的离散等效基带模型。

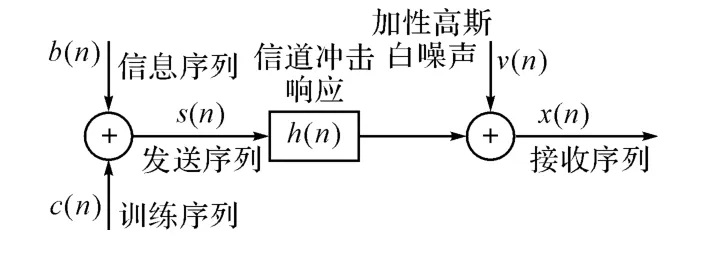
图1 离散等效基带模型

接收序列

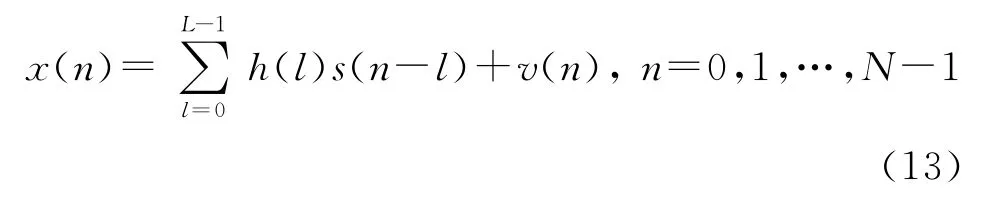
其中N为数据块长度，P为训练序列周期，K＝N／P且K为整数，L-1为非零信道冲击响应的最大延迟时间且P≥L。发送序列

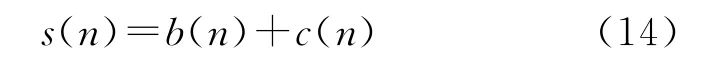
有如下假定：

（H1）信息符号b（n）根据调制方式等概率地取自有限调制符号集，均值E［b（n）］＝0，方差E［｜b（n）｜2］＝σ2b。

（H2）｛v（n）｝为加性高斯白噪声，均值E［v（n）］＝0，方差E［v（n＋τ）vH（n）］＝（τ）。

（H3）训练序列c＝1K⊗cp，cp＝［c（0），c（1），…，c（P-1）］T。为了降低峰均功率比，采用优化的时／频域恒包络训练序列。文献［10］给出了最优训练序列c（n）＝σcexp（j2πn（n＋i）／P）（当P为偶数时，i＝0；当P为奇数时i＝1，n＝0，1，…，P-1）。训练序列的平均功率＝｜c（0）｜2。

信道环境为慢时变，且无多普勒（Doppler）频率扩展。频率选择性信道的参数在一个数据块内不变，在数据块之间可以发生改变。信道冲击响应为h＝［h（0），h（1），…，h（L-1）］T。

式（13）的系统模型可以写成矢量形式

其中x＝［x（0）x（1） …x（N-1）］T，v＝［v（0）v（1） …v（N-1）］T，S为N×N维矩列循环Toeplitz矩阵的前L列组成的矩阵

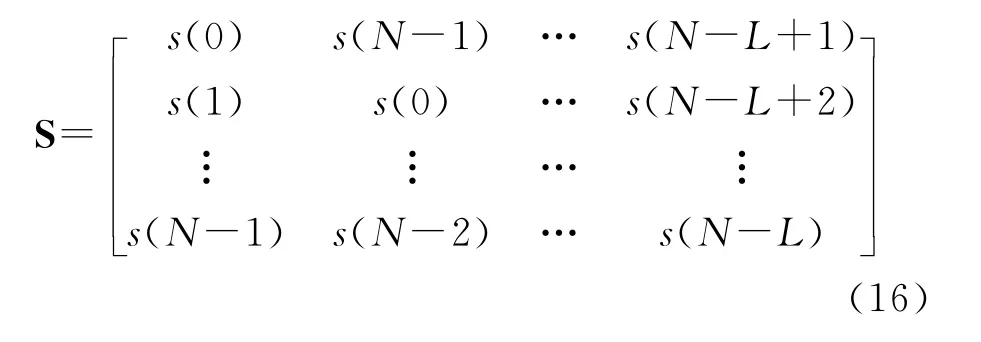
式（15）隐含在发送端加入了长度为L-1的循环前缀（Cyclic Prefix，CP），在接收端去除了CP。S的第1列为不包含CP的发送序列s。

根据式（14），式（15）可以写成

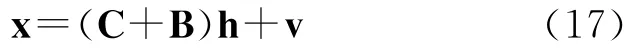
其中B和C具有与S相同的结构。

C也是一个块重复的矩阵。矩阵

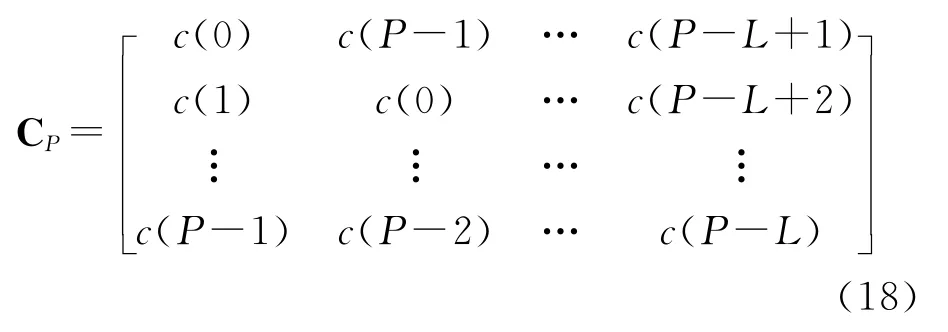
则C＝1K⊗CP。

令J＝（1／K）（⊗IP），用J左乘式（17）得到接收序列的循环均值y

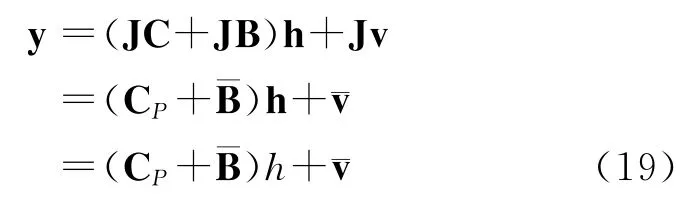
其中E［（n）］＝0，（n＝0，1，…，P-1）。也是类似于CP的Toeplitz矩阵：

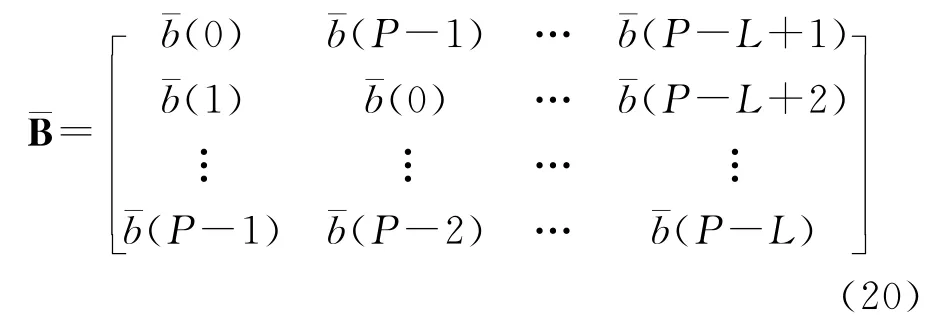
其中

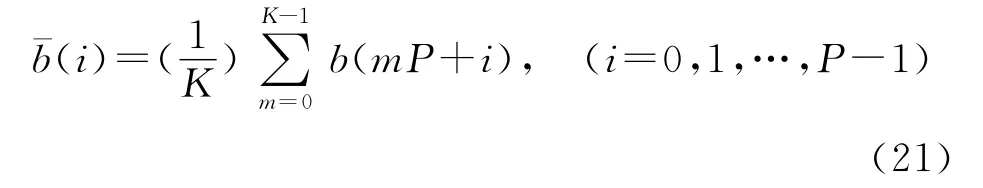
3．2 基于STLN 算法的信道估计

由于E［b（n）］＝0，E｛v（n）｝＝0，可以认为ˉB＝0。LS信道估计为

4 仿真结果与分析

仿真的信道为L＝4 的时不变频率选择性Rayleigh衰落信道。信道系数的产生方法参考文献［10］。信道冲击响应进行了归一化

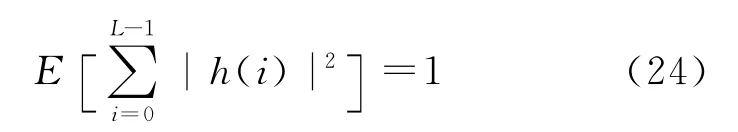
通过1000个数据块的蒙特卡罗仿真得到NC-MSE，其定义如下

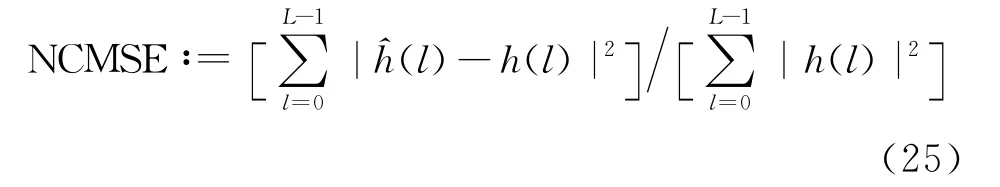
假定系统已经同步，则训练序列周期P＝9，数据块长度N＝360。发送序列的功率为＋＝1，训练序列占发送信道的功率比为／（＋）＝0．3，略微损失了发送序列的信噪比。QPSK 调制中，信息序列来自有限符号集，｛b（n）｝∈｛1，i，-i，-1｝。仿真中的信噪比（Signal to Noise Ratio，SNR）为单边噪声功率谱密度与发送序列的功率比。

图2对比了叠加训练序列的分别基于LS，DLS［2］，TLS［1］，STLN［5］的信道估计的NCMSE。仿真结果表明，本文应用的STLN 算法性能优于其他对比算法。STLN 算法的NCMSE 可以通过迭代提高精度，但是2次迭代就足够了。图3对比了基于LS，TLS，DLS，STLN 的信道估计的误差范数，也表明STLN 算法的误差范数最小。STLN 算法迭代2 次就足够了，第3 次迭代的误差范数和NCMSE的减小已经很少了。

图2 基于LS，DLS，TLS，STLN 的叠加训练序列信道估计的归一化信道均方误差

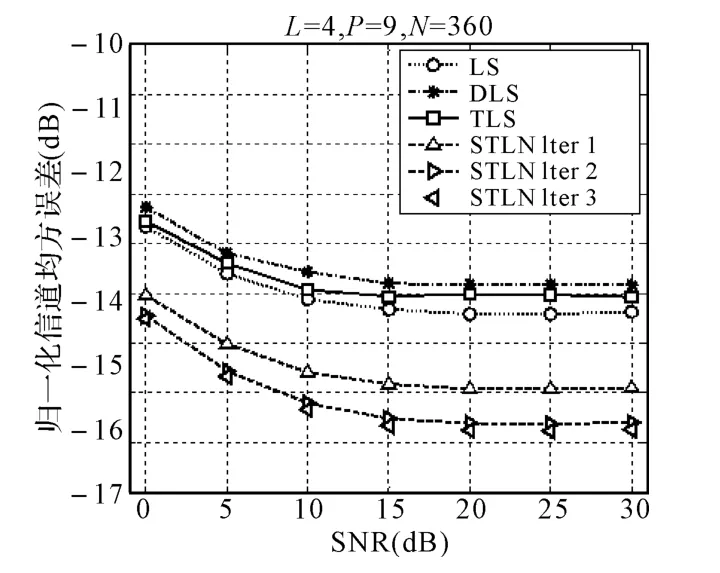
图3 基于LS，DLS，TLS，STLN 的叠加训练序列信道估计的误差范数

5 结语

TLS算法假定误差同时存在于数据矩阵和观察值中，提高了参数估计性能，但是没有考虑误差矩阵的先验信息。STLN 算法假定误差矩阵具有Toeplitz结构，而ST 信道估计中信息序列均值构成的误差矩阵也具有Toeplitz结构。本文对比了LS，DLS，TLS和STLN 算法在ST 信道估计上的应用。仿真结果表明，STLN 算法的NCMSE 最小，信道估计性能最优。

［1］G．H．Golub，C．F．Van Loan．An analysis of the total least squares problem［J］．SIAM J．Numer．Anal．，1980，17（6）：883-893．

［2］R．D．Degroat，E．M．Dowling．The data least squares problem and channel equalization［J］．IEEE Trans．Signal Process．，1993，41：407-411．

［3］T．J．Abatzoglou，J．M．Mendal，G．A．Harada．The constrained total least squares technique and its application to harmonic superresolution［J］．IEEE Trans．Signal Process．，1991，39（5）：1070-1087．

［4］张贤达．矩阵分析与应用［M］．北京：清华大学出版社，2004：404-450．

［5］J．B．Rosen，H．Part，J．Glick．Total least norm formulation and solution for structured problems［J］．SIAM Journal on Matrix Anal．Appl．，1996，17（1）：110-126．

［6］P．Lemmerling，N．Mastronardi，S．V．Huffel．Fast algorithm for solving the Hankel／Toeplitz structured total least squares problem［J］．Numerical Algorithms，2000，23：371-392．

［7］Ivan Markovsky，Diana M．Sima，Sabine Van Huffel．Total least squares methods［J］．WIREs Computational Statistics，2010，2：212-217．

［8］G．T．Zhou，M．Viberg，T．McKelvey．First-order statistical method for channel estimation［J］．IEEE Signal Process．Lett．，2003，10（3）：57-60．

［9］A．G．Orozco-Lugo，M．M．Lara，D．C．McLernon．Channel estimation using implicit training［J］．IEEE Trans．Signal Process．，2004，52（1）：240-254．

［10］M．Ghogho，D．C．McLernon，E．Alameda-Hernandez，et al．Channel estimation and symbol detection for Block Transmission Using Data-Dependent Superimposed Training［J］．IEEE Signal Process．Letters，2005，12（3）：226-9．

［11］M．Ghogho，D．C．McLernon，E．Alameda-Hernandez，et al．Channel estimation and symbol detection for Block Transmission Using Data-Dependent Superimposed Training［J］．IEEE Signal Process．Lett．，2005，12（3）：226-229．