在带锯床上切削齿轮坯的设计与分析

2014-11-22李晓芳闫其顺储连云

机械工程师 2014年3期

李晓芳，闫其顺，储连云

（1.连云港工贸高等职业技术学校，江苏连云港222069，2.连云港机床厂有限公司，江苏连云港 222023）

0 引言

在加工齿轮时我们一般选择的是滚齿或插齿的加工方法，这两种加工方法的加工精度都比较高，但是如果齿轮坯的加工余量大，滚齿或插齿的加工时间将会较长，加工效率偏低。为了能提高大尺寸齿轮的加工效率，可以先利用锯切的方法去除部分加工余量，然后再选用滚齿加工或插齿加工。

1 锯切齿轮坯的工艺

本文研究中选用卧式带锯床对齿轮坯进行粗加工，如图1 所示。图中阴影部分为需锯切掉的部分，线a 和线b为锯切路径，带锯条位于图示的垂直位置。

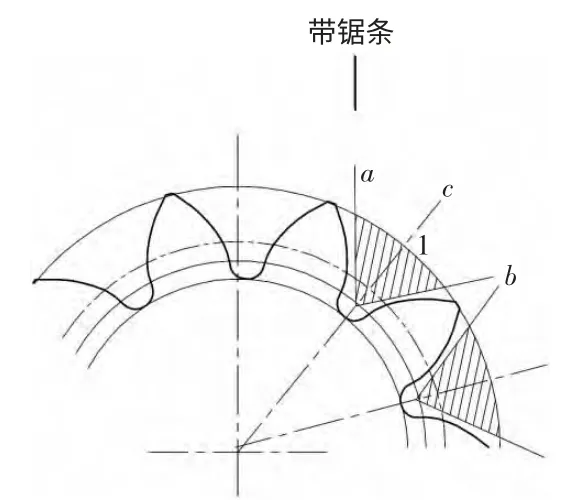
图1 锯切路线示意图

对于不同尺寸的齿轮坯，锯切线a 和b 的位置是变化的。在锯切之前应根据齿轮坯的参数，确定这两条线的位置及切深h 的数值。

1.1 齿轮参数

例如，选择齿轮的参数为：模数m＝50 mm，齿数Z＝10，压力角α＝25°＝1，c*＝0.25，变位系数x＝0.34mm。根据变位系数和齿轮的参数，可以算得节圆处的齿厚为94mm，齿顶宽度为10.37 mm，基圆齿厚为99 mm。

1.2 锯切路线设计

图2 锯切线设计示意图

在锯切时要保证齿轮轮齿的完整性，并要使轮齿各处所留的加工余量尽量均匀。再根据渐开线的形成原理，可以设计出轮齿的直线齿廓线以及锯切线，如图2 所示。在图2 中，线1为轮齿的直线齿廓（使各处加工余量最小且均匀），留滚齿（或插齿）加工余量20 mm，形成线2（即图1 中的a 线）。线3为齿槽的中心线，线4（即图1 中的b 线）为线2 相对于线3 的对称线，即下一个轮齿的左轮廓锯切线。在锯切的时候按线2 和线4 两条线进行切削即可。

1.3 齿轮安装位置设计

由于锯切齿轮坯属于粗加工，并且所加工的齿轮坯一般直径都比较大，所以在计算时根据所留加工余量尽量小以及尽量均匀的原则，对齿廓进行了拟合直线的处理，如图3 所示。图中b、c、d分别为轮齿的高度、齿顶宽度和基圆上轮齿的宽度（均为半值）［3］。a为齿顶到齿轮中心的高度。在加工时，线1（垂直于图1 中的a 线）应处于水平位置，所以在装夹好后的加工之前，齿轮坯要旋转一定的角度，即β。根据渐开线成形原理，选取齿顶圆和基圆上的轮廓曲线点为参考点进行计算［4］，计算过程如下：

齿顶宽按变位齿轮最小齿顶宽进行计算，其数值为12.5 mm（图3 中c 值），因数值较小，所以弦长取为弧长，即为12.5 mm，而基圆上的弦长为49.13 mm（图3 中d 值）。

所以角β 计算为：（42.88×317）÷112.5＋6.25＝127 mm（角β 下线长度），tanβ＝42.88/112.5，β＝20.86°。

线1 的长度为L，cosβ＝L/127，L＝118.67 mm≈119 mm。

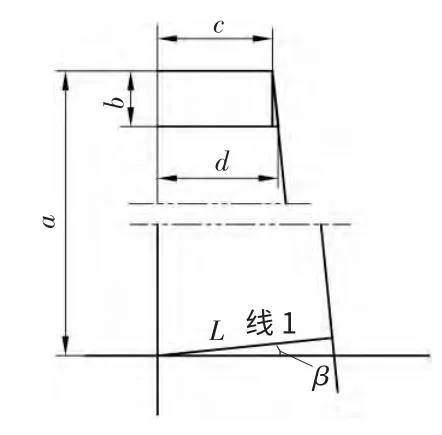
图3 齿廓拟直线示意图

考虑到齿顶圆和基圆上的渐开线点的连线的斜率是渐开线上其他点与基圆上的点连线的斜率中最大的，所以，实际渐开线形状应该是在两点连线的右方，以分度圆为计算点［5］，切线应右移的距离为：47－（67×49.13÷112.5+6.25）＝47-35.5＝11.5 mm。

因为要留加工余量20 mm，所以偏心距为e＝119+20+11.5≈150 mm。初始旋转角度为：β＝21°。

其初始加工位置如图4 所示。在切轮齿左侧的槽时，齿轮坯逆时针旋转42°，并向前方移为300 mm。根据同样的计算原理，选取分度圆和基圆上的轮廓曲线点为参考点进行计算，得到锯切位置线如图5 所示。对比图4 和图5，可知图4 所留的加工余量更均匀。

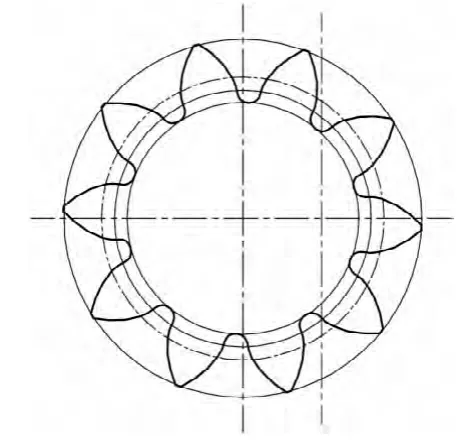
图4 以齿顶圆为基准的锯切位置图

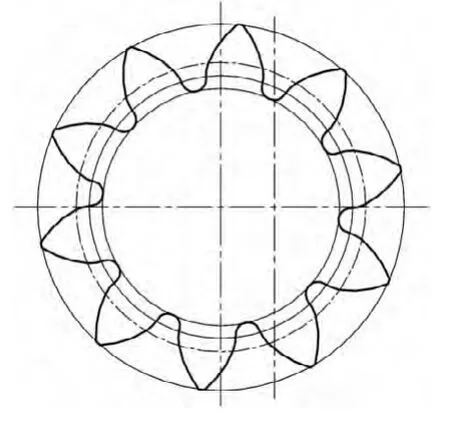
图5 以分度圆为基准的锯切位置图

1.4 锯床切深的计算

如图1 所示，直线a 的方程为x＝150。

斜线c 的方程为：y＝xtan（90°-18°-21°）＝xtan51°。所以二者交点处y 值为：y＝xtan51°＝150×tan51°＝185.23 mm。

因为齿顶圆方程为：x2+y2＝（633/2）2，所以当x＝150时，y＝278.7 mm。有效切深L1＝278.7-185.23＝93.47 mm，为了能保证一个齿槽内两条切线能有交点，所以加切深量为93.47+5＝99 mm。在选择带锯床下移距离时，以齿顶圆为参照物，所以带锯床锯条下移距离为：h＝316.5-185.23+5≈137 mm。