水下环肋圆柱壳弹性失稳临界载荷无损预报方法

陈 忱，李天匀，朱 翔，陈浩森

(华中科技大学 船舶与海洋工程学院，湖北 武汉 430074)

环加筋圆柱壳在水下工程中被广泛使用，其临界载荷的大小关系到结构体的安全性，因此，大量学者对此进行了深入的研究。早期，Bijlaard［1］提出了研究临界载荷的几种方法:数值分析方法、试验法及理论解析法。数值分析方法建模工作量大、计算时间长;试验方法代价高、周期长。针对前两种方法的不足，近年来求解临界载荷的理论解析方法得到了广泛应用。Singer 等［2］利用振动频率特性预估失稳载荷的方法对加筋圆柱壳进行研究，发现在屈曲前高载荷处的频率急剧下降。王震鸣等［3］分别采用剪切变形理论和经典扁壳理论得到了加筋圆柱壳在受轴向、侧压及剪切作用力时的失稳临界载荷，并分析了两种理论下产生失稳临界载荷误差的原因。Raymond［4］揭示了固有频率平方与临界载荷的关系，并预测光壳临界载荷的上下限，为临界载荷无损预报方法打下了基础。

将环肋对壳体振动的影响参数和静水压力所产生的预应力计入到壳体振动方程中，研究静水压力和固液耦合系统固有频率的关系，进而利用这一关系得出给定边界条件、给定模态下环肋圆柱壳的临界载荷，实现水下环肋圆柱壳临界载荷的无损预报。

1 研究对象

以浸没在水中的流场-内环肋圆柱壳耦合系统为研究对象。假设圆柱壳体为薄壳，壳体厚度为h，中面半径为R，材料密度为ρs，弹性模量为E，泊松比为μ;环肋的间距为d，筋条的高度为a，宽度为b，环肋材料的弹性模量为E1，剪切模量为G1;流体密度为ρf，声传播速度为Cf;壳体所受的静水压力为P0，流体声载荷为Pf。以x，θ 和r 分别表示壳体的轴向、周向和径向;u，v 和w 表示壳体中面轴向、周向和径向位移。环肋圆柱壳的坐标系与周向模态数n 如图1 所示，肋骨示意如图2 所示。

图1 环肋圆柱壳坐标系和周向模态数nFig.1 Coordinate system and circumferential modal shapes

图2 肋骨示意Fig.2 Picture of siffness

2 水下环肋圆柱壳的自由振动方程

2.1 壳体振动方程

基于经典Flügge 方程理论和正交各向异性的近似处理方法，可以得到计及外压的环向加肋圆柱壳自由振动Flügge 方程［5］:

矩阵［G］3×3的各元素表达式如下，

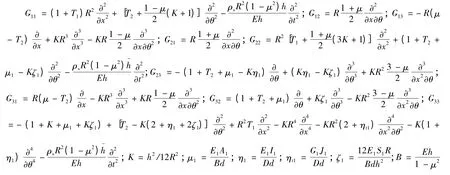
需指出，这里把加筋圆柱壳简化为正交各向异性圆柱壳进行研究，将环筋条的刚度和质量“平均”在壳体的周向上，因此，筋条密些，所得结果更精确。

2.2 耦合声振方程

流体声载荷Pf满足柱坐标系下的Helmholtz 波动方程:

壳体振动时周向取驻波形式的解，而考虑振动波沿壳体轴向的传播，将中面位移展开成为与壳体的轴向波数有关的简正波形式:

式中:Uns，Vns，Wns为中面位移幅值，ω 为圆频率(rad/s)，kns为轴向波数，s 为频散方程中轴向波数解的序号。

对于声压场，用分离变量法求解Helmholtz 方程，并考虑辐射条件以及壳壁处的耦合边界条件，满足波动方程的流体声压场有如下形式的解:

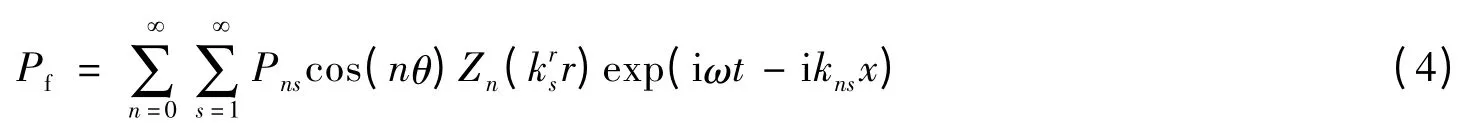
式中:Pns为流体声载荷幅值，为径向波数，为流体中的自由波数。为Bessel 函数;由于圆柱壳浸没于流场中，则有:为n 阶第二类Hankel 函数。在流体与壳体的接触面上，流体径向位移必须等于壳体的径向位移，即:

将式(3)和式(4)代入式(5)中，对每一组(n，s)可得到流体的声压幅值:

将式(3)、(4)、(6)代入式(1)中，便得到此耦合系统的自由振动方程，用矩阵形式表示:

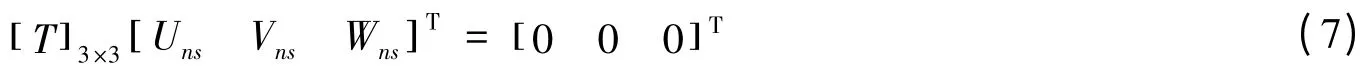
矩阵［T］3×3的各元素表达式，

T11= Ω2－(1 +T1)λ2－［T2+(1 －μ)(K +1)/2］n2;T12= －iλn(1 +μ)/2 ;T13= i［(μ －T2)λ +Kλ3－ K(1 －μ)λn2/2］;T21= iλn(1 +μ)/2 ;T22= Ω2－［T1+(1 －μ)(1 +3K)/2］λ2－(1 +μ1－Kη1+T2)n2;T23= (1 + μ1－ Kη1+ T2)n + (Kη1－ Kζ1)n3+ Kλ2n(3 － μ)/2 ;T31= － i［(μ － T2)λ + Kλ3－ K(1 －μ)λn2/2］;T32= (1 + μ1+ T2)n － Kζ1n3+ Kλ2n(3 － μ)/2 ;T33= － (1 + μ1+ K + Kζ1)－［T2－ K(2 + η1+2ζ1)］n2－ T1λ2－ Kλ4－ K(2 + ηt1)λ2n2－ K(1 + η1)n4+ Ω2－ FL。

式(7)有非零解的条件是矩阵行列式为零，即为描述无量纲轴向波数kns与无量纲频率Ω 关系的特征方程:

2.3 边界条件

由式(8)知，为得到环肋圆柱壳的固有频率，轴向波数kns必须满足一定的边界条件。基于正交各向异性理论，已将环肋的刚度均摊到壳体上，在低频范围内按低阶模态振动时，可以运用Lam 等［6］提出的关于不同边界条件下水下圆柱壳轴向波数的计算公式，其中m 表示振动时的轴向半波数。

将表1 给出的相应公式代入式(8)，就可求得在一定的静水压力下耦合系统的无量纲频率，得出关于水下环肋圆柱壳静水压力和固有频率的关系，进而对临界载荷进行无损预报。

表1 不同边界下的轴向波数Tab.1 axial wave numbers under different boundaries

3 水下环肋圆柱壳临界载荷和固有频率的关系

3.1 模型可靠性验证

耦合系统的特征方程(8)是一个复平面上的高阶超越方程。用Muller 三点迭代法进行Matlab 编程，采用Pasly［7］和chu［8］的计算模型进行程序可靠性分析。

采用文献［7］和［8］中的计算数据:壳体弹性模量E =2.068 ×1011N/m2，泊松比μ =0.3，密度ρs=8 300 kg/m3，壳厚h=4.496 mm，半径R=0.514 4 m，壳长L=1.289 m;环肋材料与壳体相同，弹性模量E1=2.068 ×1011N/m2，剪切模量G1= 0.8 ×1011N/m2，环肋高度a=45.29 mm，环肋宽度b=4.597 mm，肋骨间距d1=85.72 mm，筋条数目N=14;流体自由波传播速度Cf=1 524 m/s，流体密度ρf=997.7 kg/m3;静水压力P0=14.9 kPa，边界条件为两端简支。对比结果如表2 所示。

表2 列出了Pasly 的试验结果和Chu 使用Donnell 方程的计算结果。可以看出，文中程序计算结果与Pasly 和Chu 给出的结果都存在一定的误差，但在许可范围内，且规律是一致的。存在误差是因为所采用的理论模型不同:这里采用正交各向异性板壳模型，把筋条的刚度“平均”在面板上;Chu 则采用基于Donnell理论和能量法的离散模型，充分考虑了筋条导致的结构不连续的影响，各内力成分用离散级数的形式给出，筋条仅在各自的位置上相互作用;而Pasly 采用的试验模型在环肋圆柱壳两边各加了一段光壳，影响了环肋结构的简支边界条件，因而导致该试验结果与chu 的理论结果及本文计算结果的误差。

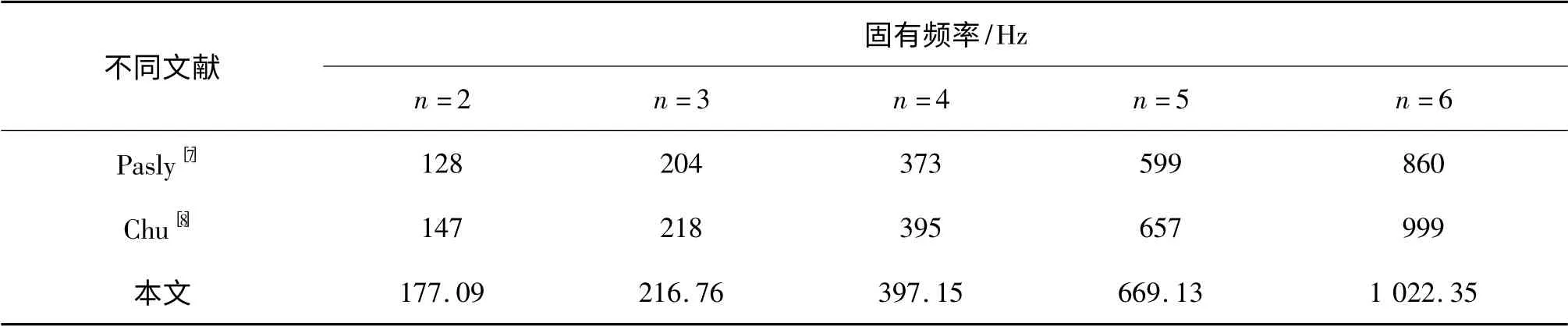
表2 m=1 时静水压力下的环肋圆柱壳固有频率Tab.2 Frequencies of ring-stiffened cylindrical shells under hydrostatic pressure(m=1)

3.2 两端简支环肋圆柱壳的固有频率及临界载荷

采用上节的壳体参数，计算两端简支环肋圆柱壳在不同静水压力下的固有频率，所得结果如表3 所示(m=1)。

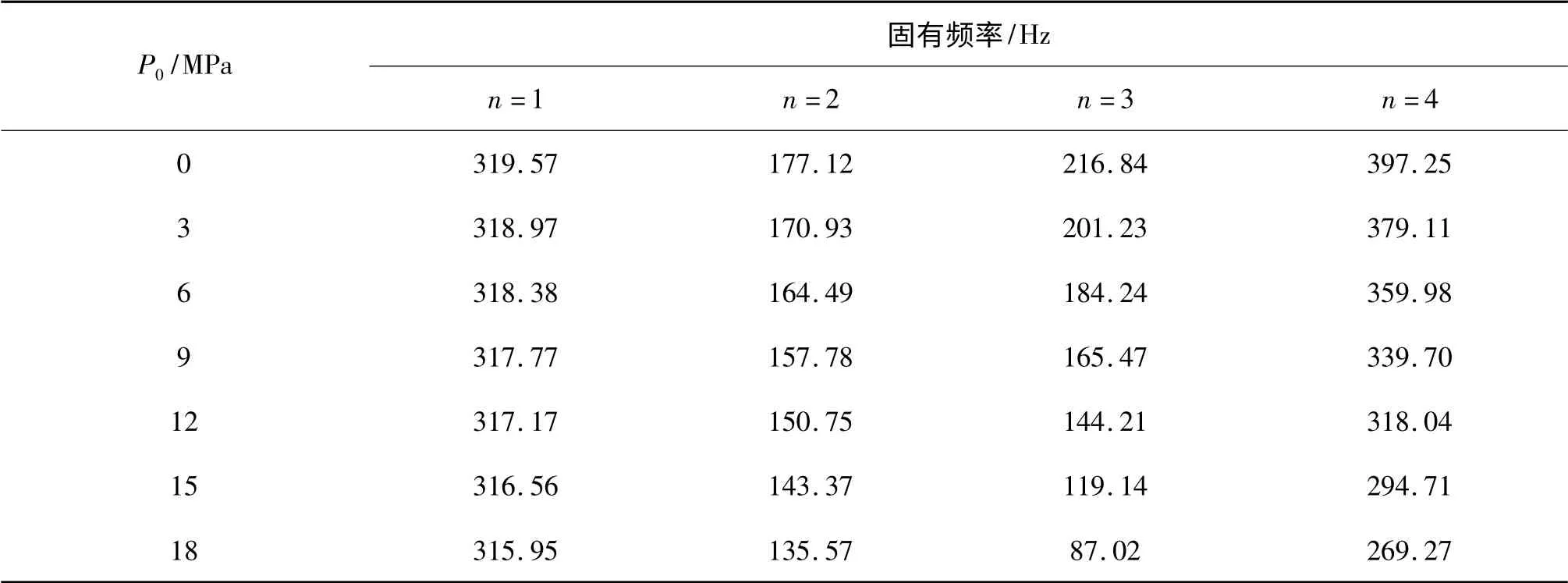
表3 两端简支环肋圆柱壳的固有频率Tab.3 Frequencies of simply-supported ring-stiffened cylindrical shell

图3 简支环肋壳固有频率平方与静水压力的关系Fig.3 Relationship between frequency squared and hydrostatic pressure of simply-supported ring-stiffened cylindrical shell

从表3 可知，各模态下环肋圆柱壳的固有频率随静水压力的增加而减小，但减小速率各不同。现将模态(1，2)和模态(1，3)对应的固有频率的平方与外压的关系绘于图3 中。

从图3 可看出，环肋圆柱壳固有频率的平方与静水压力近似呈线性关系。考虑用f2= ka(P0－Pcr)来描述它们的关系，f 是环肋圆柱壳的固有频率，Pcr是环肋圆柱壳的临界载荷，ka是用最小二乘法得出的拟合直线斜率。经计算，模态(1，3)对应的拟合直线斜率ka= －0.219 5 Hz2/MPa。同时，给定边界条件下任意模态(m，n)对应的固有频率平方与静水压力也近似成线性关系。这与文献［9］和［10］中的结论是一致的。

圆柱壳失稳时，结构体的刚度丧失，固有频率为零。若能求出在不同模态(m，n)下频率为零时对应的静水压力(图3 中实线与横轴交点的横坐标)的最小值，则此压力即可认为是该环肋圆柱壳临界载荷的最小弹性理论解。由表3 和图3 可知，模态(1，3)对应的拟合直线与横轴交点的横坐标最小，则知该模态为环肋圆柱壳的失稳模态，其频率为零时对应的静水压力即为该环肋圆柱壳的临界载荷。用最小二乘法得出的拟合直线方程为f2= －0.219 5(P0－21.45)，则知该两端简支环肋圆柱壳的最小临界载荷Pcr为21.45 MPa。

按两端简支条件下径向、轴向承受静水压力的环肋圆柱壳临界载荷米塞斯公式(针对中等长度壳，n =2～3)，可得到理论值［11］:

式中:a1= πR/L 为壳体长度参数;J 是肋骨截面与附连板对其中性轴的惯性矩。代入计算模型数据，则得临界载荷的理论值Pcr= 21.83 MPa，这与文中拟合曲线求得的计算结果21.45 MPa，相对误差为－1.74%，也进一步证实了本方法的正确性。

为了方便验证，采用了文献［7］和［8］的中等长度壳体计算模型。而对于细长壳(n =2)，应该按照希曼斯基公式计算理论临界载荷。

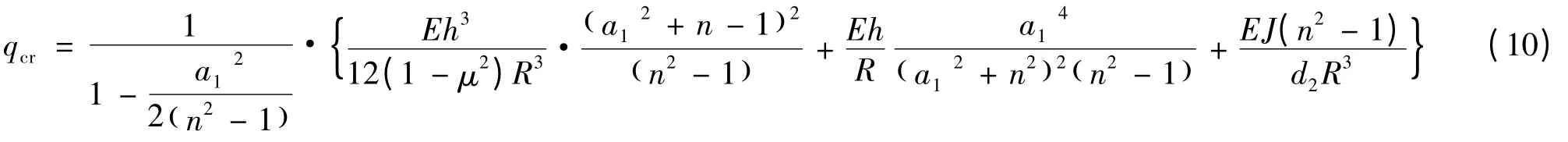
计算分析表明，其规律性是一致的。

3.3 其它边界环肋圆柱壳的固有频率及临界载荷

采用3.2 节给出的计算模型，不同边界条件环肋圆柱壳的固有频率及其临界载荷如表4、表5 及图4 所示(m=1，n=3)。由图4 知，给定模态的不同边界条件环肋圆柱壳的固有频率平方与静水压力也近似成线性关系。并且边界条件不同，环肋圆柱壳的临界载荷也不同，两端刚固(C-C)时的临界载荷比其他边界条件的临界载荷要大，说明边界约束越强，环肋圆柱壳的临界载荷越大。

图4 不同边界条件下固有频率平方与静水压力的关系Fig.4 Relationship between frequency squared and hydrostatic pressure of ring-stiffened cylindrical shell under different boundaries

表4 不同边界下环肋圆柱壳的固有频率Tab.4 Frequencies of ring-stiffened cylindrical shell under different boundaries

表5 不同边界下环肋圆柱壳的临界载荷Tab.5 Buckling loads of ring-stiffened cylindrical shell under different boundaries

以上计算得到的是静压下环肋圆柱壳临界载荷的弹性理论解。对求得的临界载荷值还要经过几何非线性修正和物理非线性修正［12］，才能应用于工程设计中。

4 结 语

运用正交各向异性理论求出水下环肋圆柱壳临界载荷的弹性理论解。基于Flügge 壳体理论建立了水下环肋圆柱壳固－液耦合系统自由振动方程，基于波传播法得到了水下环肋圆柱壳的固有频率，进而通过线性拟合得出水下环肋圆柱壳临界载荷的弹性理论解。计算结果表明，任意边界的同一模态下，固有频率平方与静水压力成正比，且边界约束越强，环肋圆柱壳的临界载荷越大，其中两端刚固(C-C)时的临界载荷最大。与相关文献的数值计算结果进行对比，表明了本方法及程序的准确性，它为水下环肋圆柱壳临界载荷的无损预报提供了一种新的方法。

［1］Bijlaard P P.Theory and tests on the plastic stability of plates and shells［J］.Journal of the Aeronautical Sciences，1949，16(9):529-541.

［2］Singer J，Prucz J.Influence of initial geometrical imperfections on vibrations of axially compressed stiffened cylindrical shell［J］.International Union of Theoretical and Applied Mechanics，1976:227-250.

［3］王震鸣，戴涪陵，吕明身.复合材料的多层、夹层和加筋圆柱曲板的稳定和振动［J］.固体力学学报，1984:517-531.(WANG Zhen-ming，DAI Fu-ling，LU Ming-shen.Stability and vibration of laminated，sandwished and stiffened cylindrical shells［J］.Journal of Solid Mechanics，1984:517-531.(in Chinese))

［4］Raymond H.Use of frequency data to predict bulking loads［J］.Journal of Sound and Vibration，1990，116(10):2330-2335.

［5］中国科学院力学研究所.加筋圆柱曲板与圆柱壳［M］.北京:科学出版社，1983.(Institute of Mechanics in Chinese Academy of Sciences.Stiffened Cylindrical Curved Plates and Cylindrical Shells［M］.Beijing:Science Press，1983.(in Chinese))

［6］Lam K Y，Loy C T.Effects of boundary conditions on frequencies of a multi-layered cylindrical shell［J］.Journal of Sound and Vibration，1995，188(3):363-384.

［7］Pasly R B，Tatge R B，Wernick R J，et al.Vibration characteristics of a submerged ring-stiffened cylindrical shell of finite length［J］.J.Acoustic.Soc.Ame，1969，46(3):701-710.

［8］Chu K K T，Pappa M，Herman H.Dynamic of submerged cylindrical shells with eccentric stiffening［J］.AIAA，1980，18(7):834-840.

［9］Souza M A，Assaid L M B.A new technique for the prediction of buckling loads from nondestructive vibration tests［J］.Experimental Mechanics，1991:93-97.

［10］李范春，杜 玲，刘清风，等.受压结构稳定性的无损检测分析方法研究［J］.船舶力学，2010，14(4):393-398.(LI Fan-chun，DU Ling，LIU Qing-feng，et al.No damage testing analyzed method research of the compress structure stability［J］.Journal of Ship Mechanics，2010，14(4):393-398.(in Chinese))

［11］吴连元.板壳理论［M］.上海:上海交通大学出版社，1989.(WU Lian-yuan.Shell Theory［M］.Shanghai:Shanghai Jiao Tong University Press，1989.(in Chinese))

［12］刘 涛.大深度潜水器耐压壳体弹塑性稳定性简易计算方法［J］.中国造船，2001，42(3):9-14.(LIU Tao.Simplfied method of in elastic buckling analysis of deep submersible pressure hull［J］.The Shipbuilding of China，2001，42(3):9-14.(in Chinese))