MPS 方法数值模拟液舱晃荡问题

张雨新，万德成，日野孝则

(1.上海交通大学 船舶海洋与建筑工程学院 海洋工程国家重点实验室，上海 200240;2.横滨国立大学 工学府，日本 横滨)

液舱晃荡是船舶流体力学研究的热点问题，其流动现象十分复杂，常带有自由面的翻卷、融合、破碎和液体的飞溅等现象。晃荡对液舱壁面产生的抨击压力可能会造成结构的破坏，并且影响船舶航行的稳定性。因此，对晃荡载荷的预测是船舶航行安全性评估的重要内容之一。

早期对晃荡的研究常借助于实验［1-2］，但实验周期长、费用高，提供的信息有限，且常常存在尺度效应。随着计算机的发展，数值模拟逐渐成为研究晃荡问题的重要手段。早期的数值求解是基于势流理论，如Faltinsen［3］发展了边界元方法(boundary element method，BEM)用来研究非线性晃荡问题，Wu 等［4］基于有限元(finite element method，FEM)对三维晃荡进行了研究，Frandsen［5］开发了一个完全非线性的有限差分(finite difference method，FDM)求解器来分析晃荡中波形的变化。但基于势流的研究方法忽略了粘性的影响，不能预测近壁面处粘性主导的流动现象，同时难以处理一些复杂的自由面变形，如破波、翻卷等。近二十年来，基于粘流的CFD 技术发展迅速，并被越来越多地用来研究复杂的晃荡问题。准确预测晃荡压力的一个关键就是追踪自由面，为此人们提出了许多方法。这些方法大部分是基于网格系统的，如Chen 等［6］利用两相Level-set 方法分析了矩形液舱在不同水深及频率下晃荡产生的抨击压力;Liu 等［7］开发了基于VOF(volume of fluid)的两相求解器用来研究三维六自由度的剧烈晃荡现象;Hu 等［8］改进了CIP(constraint interpolation profile)方法，并对二维、三维剧烈晃荡问题进行了研究;郭晓宇等［9］基于两相VOF 方法对低充水液舱的气垫效应进行了分析。

近年来，无网格粒子法发展较快，与传统的网格类方法相比，粒子法具有较大的灵活性，易于处理一些大变形的自由面问题，其中SPH (smoothed particle hydrodynamics)［10-11］和MPS (moving particle semiimplicit)［12-13］是两种常用的粒子法。这两种方法都有各自的优缺点［14］，SPH 的计算效率较高，适于大规模并行计算，但其流体是弱可压缩的，计算时需要较小的时间步长来满足CFL 条件。而MPS 方法则是通过Poisson方程隐式求解压力，可以接受较大的时间步长，其流体是真正不可压缩的。由于粒子法在处理自由面流动问题具有较大的灵活性，因此常被用来研究复杂的流动问题，如溃坝、破波、晃荡等。Delorme 等［15］利用SPH 对浅水液舱晃荡进行了研究，数值模拟很好地预测了抨击现象，但SPH 给出的压力与实验存在较大的偏差。Colagrossi 等为了改进SPH 的压力计算精度引进MLS(most least square)格式对密度进行积分［16］，提高了压力场的光滑性，并对剧烈晃荡问题进行了研究［17］，数值得到的抨击压力变化曲线能够比较好地与实验吻合，但仍存在一定程度的振荡。Khayyer 等［18］提出了一种高阶Laplacian 模型的MPS 方法，并以晃荡问题为例进行了验证，结果表明高阶的Laplacian 模型能够改善压力的预测精度。Lee 等［19］基于MPS 对晃荡进行了研究，并对MPS 做了一系列的改进，包括核函数、压力Poisson 方程的源项优化、粒子碰撞模型，数值得到的压力能够很好地与实验吻合，不过其粒子碰撞模型中带有较大的非物理因素。在国内，崔岩等［20］利用SPH 对二维矩形液舱的晃荡进行了分析，数值得到的波高能够与实验一致。陈正云等［21］基于SPH 数值模拟了大幅晃荡问题。潘徐杰等［22-23］利用MPS 研究了二维高充水率液舱晃荡问题，并针对MPS 的压力振荡问题进行了讨论。

虽然粒子法已在晃荡问题中显示出了较好的灵活性，能够处理剧烈晃荡时复杂的自由面变形，但粒子法仍然存在许多问题需要解决。如何改进粒子法并获得稳定光滑的压力场是十分重要和值得探讨的，另外，对于晃荡中抨击压力预测的可靠性还需要更多的验证。本文的主要目的是应用MPS 方法对液舱晃荡问题进行研究，然而传统的MPS 方法中压力振荡十分明显，目前已有一些学者提出了改进方法。Sueyoshi［24］建议对压力进行时间和空间上平均，这是参照压力应变片的工作原理，这种方法能够给出较为合理的压力结果。但对于数值计算而言这是一种后处理方法，难以用于带有浮体的流动问题。Hibi［25］提出求解压力Poisson 方程(PPE)两次。第一次求解的PPE 与传统的方程一样，而第二个PPE 则采用速度散度作为方程的源项，得到的压力用来对前一个压力进行修正。然而，这个修正压力没有参与粒子的移动，因此这种方法并不能提高计算的稳定性，并且增加了计算量。Khayyer 等［26］提出了高阶源项法，其中源项是对通过粒子数密度求导得到的，此外还提出了弱可压缩的MPS 方法，数值结果表明这两种方法对于压力有一定程度的改善。Tanaka［27］提出了一种混合源项法，这种方法结合了粒子数密度和速度散度作为PPE 的源项。其重要部分是速度源项，而粒子数密度的保留仅是为了保证流体体积的守恒。由于速度场比较光滑，因此混合源项法可以很大程度地光滑压力。

除了PPE 源项对压力有较大影响外，自由面的判断精度对压力计算的影响也很大，Koshizuka［13］讨论了自由面判断参数对自由面粒子数和自由面形状的影响，给出了参数的合理范围，但没有讨论其对压力的影响。Ataie-Ashtiani［28］分析了粒子作用域半径对自由面粒子数的影响，但同样没有涉及压力。Tanaka［27］改进了传统的自由面判断方法，即采用邻居粒子数而非粒子数密度来判断自由面粒子，这种判断方法在某种程度上提高了自由面的判断精度，但其精度仍然有限。作者曾提出了一个新的判断方法，即基于邻居粒子的不对称性来判断，数值验证表明其判断精度很好。

目前，MPS 方法在晃荡问题中的应用还相对较少，对于其预测抨击压力的可靠性还需要进一步验证，因此将利用MPS 方法对二维液舱的晃荡问题进行研究。为了消除传统MPS 方法中压力振荡问题，采用了一些改进方法，如:1)无奇点的核函数;2)混合源项法;3)更加精确的自由面判断方法。基于改进后的MPS 方法对二维液舱在不同的激励频率和运动方式时的晃荡进行了数值模拟，分析了波形的变化和特点，并将数值预测得到的压力与实验结果进行对比，验证了MPS 方法的可靠性。

1 数值方法

1.1 控制方程

对于粘性不可压缩流体，控制方程包括连续性方程和N-S 方程，可写成如下形式:

式中:ρ 为流体密度，P 为压力，V 为速度向量，g 为重力加速度向量，ν 是运动粘性系数。式(1)和式(2)的时间导数项是以物质导数形式给出的。在粒子法中，粒子的位置和其他物理量都是基于拉格朗日描述法表达的，因此不需要计算对流项。

1.2 粒子作用模型

在粒子法中，粒子间的相互影响是通过核函数来实现的。核函数的形式可以有很多种。在MPS 中常用的核函数是由Koshizuka 等［5］给出的:

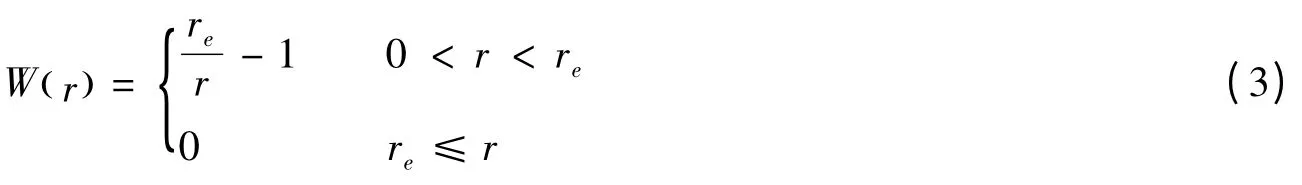
式中:r =| rj－ri| 为两个粒子间的距离，而下标i 和j 表示粒子编号;re为粒子作用域的半径，一般取一适当的有限距离。

式(3)所示的核函数一个最大的特点就是在零点处有奇异性，根据Koshizuka 的建议，这样做可以避免粒子的聚集，保证流体的不可压缩性。但在模拟流动变化剧烈的问题时，两个近距离的相邻粒子易造成过大的排斥力而影响计算的稳定性。这里采用另一种核函数［29］:

式(4)与式(3)的形式相似，但没有奇点，这样既可以避免粒子的聚集，又可以使两个距离很近的粒子不会产生过大的压力，有利于计算的稳定性。

1.3 梯度模型

梯度算子的离散可表示成径向函数的加权平均。例如对于粒子i，其压力梯度可写成［30-31］:

其中:D 为空间维数，n0为初始粒子数密度。在MPS 方法中，粒子数密度定义为:

式(5)是满足动量守恒的，其形式与SPH 中的梯度模型相似，其中粒子j 对i 的影响与i 对j 的影响是相同的，且压力将是对称的推力。

1.4 Laplacian 模型

在MPS 方法中，Laplacian 模型是由Koshizuka 等［32］给出的，其公式为:

其中:

式(7)是一种守恒格式，其推导源于非定常扩散问题，λ 的引入是为了使数值结果与扩散方程的解析解相一致。

1.5 时间积分

MPS 中一个时间步的计算过程是分成两步完成的:基于质量力和粘性力的显式修正以及压力的隐式修正。具体求解过程如下:

1)以粘性力和质量力为源项对粒子速度进行显式修正，获得临时速度V*i ，并使粒子按照该速度移动至临时位置r*i :

其中:Δt 为时间步长。

2)计算粒子在临时位置处的粒子数密度n*。

3)求解压力Poisson 方程，获得下一时刻的压力:

4)根据求得的压力，对速度和粒子位置进行隐式修正:

式(11)中的右端项为压力Poisson 方程的源项。从式中可以看到，源项的大小取决于粒子数密度与初始值的差值。在传统MPS 方法中，不可压缩条件就是通过保持粒子数密度为常数来实现的，由于粒子数密度场不光滑，式(11)给出的压力常常存在着强烈的非物理振荡。Tanaka 等［14］把速度散度加入到了压力Poisson方程的源项，并保留了粒子数密度项，Lee［19］将这种混合源项法写成如下更合理的表达式:

其中:γ 为一参数。当γ = 1 时，上式与传统MPS 方法表达式相同;当γ = 0 时，Poisson 方程源项则完全由速度散度决定。一般而言γ 越小压力场越光滑，但过小的γ 容易造成流体体积的不守恒，根据数值测试γ ≥0.01 时流体体积能够保持不变，因此这里取γ = 0.01。

1.6 自由面的判断

在MPS 方法中，自由液面的判断相对较为简单，当粒子的数密度＜n ＞*

i 满足:

时即被判定为自由面粒子。在求解压力Poisson 方程时，自由面粒子被指定0 压力边界条件，而β 是一参数，通常取β = 0.98 。

式(15)的判断精度不高，当内部粒子具有较小的数密度时容易被误判为自由面粒子，从而被赋以0 压力值，这导致误判粒子周围不正确的压力场。文中采用另外一种自由面判断方法［33］，首先定义矢量:

时即被判定为自由面粒子，其中α 为一参数。取α = 0.9 | F|0，| F|0为初始时自由面粒子的| F| 值。

需要注意的是，式(17)仅被应用于满足0.8n0＜n*＜0.97n0的粒子。这是因为n*≤0.8n0的粒子其粒子数密度过小应该被判定为自由面粒子，无需进行多余的判断，而0.97n0≤n*的粒子不是自由面粒子，应该参与压力Poisson 方程的求解。

2 数值结果及分析

本节将MPS 方法应用到液舱晃荡问题计算中，首先对一个矩形液舱纵荡时的晃荡进行模拟，将计算得到的和实验测得的压力进行对比，验证文中采用的数值方法的可靠性，同时计算一个较复杂的晃荡问题，即带隔板的液舱晃荡问题，分析隔板的存在对液体运动的影响。

2.1 矩形液舱晃荡

计算模型为二维矩形液舱，大小为0.8 m(L)×0.5 m(H)，如图1 所示。为了便于与实验结果进行比较，在舱壁上设置了2 个压力监测点，实验数据来自于DSME(Daewoo Shipbuilding ＆ Marine Engineering Co.，Ltd.)研究所。舱内水深为0.25 m，对应的填充率为50%。液舱做受迫纵荡运动，运动方程如下:

式中:a=0.02 m 为运动幅值，ω =6.469 rad/s 为激励频率。

计算所用的总粒子数为14 312 粒子，其中流体粒子数为12 338，其他为边界粒子，对应粒子间距为0.004 m。水的密度设为1 000 kg/m3，重力加速度取为9.8 m/s2，运动粘性系数ν=1.01 ×10－6m2/s。

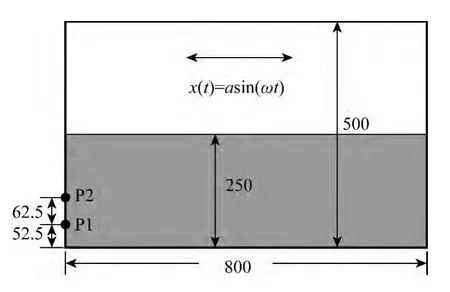
图1 液舱几何模型(单位mm)Fig.1 Geometry of tank (Unit:mm)

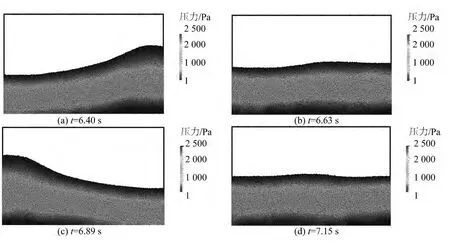
图2 不同时刻的晃荡流动瞬间Fig.2 Snapshots of sloshing flows

图2 给出了不同时刻的流场瞬间，可以看到流体以驻波的方式在舱内运动，由于该晃荡的激励频率与共振频率相差较大，因此没有发生共振现象。图3 对比了P1 处压力的实验和数值结果。可以看到，晃荡产生了明显的拍击现象，由于流动没有发生破碎等复杂现象，因此拍击压力的变化整体上很有周期性。MPS 的计算结果能够很好地与实验吻合，压力峰值和拍击的时刻都能够与实验相一致。这表明文中采用的MPS 方法能够较好预测晃荡问题中的拍击压力变化。

2.2 二维带隔板液舱晃荡

从上节的算例中可以看到，液体晃荡对舱壁产生了较大的冲击力，在工程实际中，为了减小晃荡载荷，人们有时会在舱内加入隔板来减小晃荡幅值。隔板的存在会对流动产生较大的影响，隔板附近的流动较剧烈，这给数值计算带来一定的影响。本节针对一个二维带垂直隔板的液舱晃荡问题进行研究，验证MPS 方法在带有隔板的晃荡问题中的计算可靠性。计算模型如图4 所示，液舱长为0.57 m，高度为0.5 m，舱内水深为0.18 m，对应充水率为36%。舱内带有一垂直隔板，隔板高度为0.15 m，隔板厚度为0.006 m。液舱运动幅值为a=0.1 m，激励频率为ω =3.53 rad/s。为了记录水面的高度变化，在液舱内设置了三个波高探测器，分别位于(a)x= －0.275 m;(b)x=0 m;(c)x= +0.275 m。坐标轴中心位于初始时自由面中心处。粒子间距取0.002 m，总粒子数为27 780，其中流体粒子为25 560，其他为边界粒子。

图3 压力随时间变化曲线的实验与数值结果对比Fig.3 Comparison of impact pressure between experimental and numerical results

图4 带隔板液舱的几何尺寸(单位:m)Fig.4 Geometry of baffled tank (Unit:m)

图5 给出了不同时刻下的流场瞬间，可以看到隔板的存在极大地影响了液体的水平运动，隔板左侧大部分水体的流动速度很小。隔板附近的流动较剧烈，当水流流过隔板上部时呈现出了较大的速度，该水流撞入另一侧的液体中，造成流场强烈的紊动，可以观察到自由面的翻卷、破碎和融合等现象，采用的MPS 方法能够很好地模拟这一现象。图6 对比了不同波高监测处的水面高度随时间变化曲线，计算与实验结果［34］较好地吻合，波高的峰值和相位都能够与实验一致。图6 还给出了VOF 的计算结果［34］，相对于VOF 方法，MPS的波高幅值与实验更接近，尤其是在x=0 m 位置，从图中能够看到，x=0 m 位置处正是流动最剧烈的地方，MPS 能给出较好的结果主要是因为粒子法更易处理这类剧烈的自由面流动。

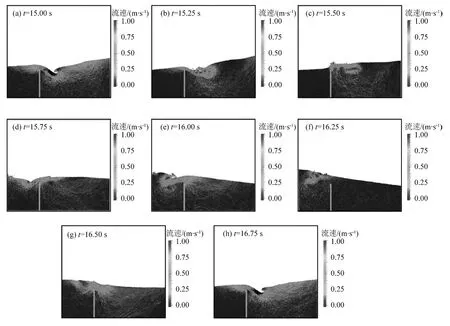
图5 二维带隔板液舱晃荡流动瞬间Fig.5 Snapshots of sloshing in baffled tank

图6 波高随时间变化曲线Fig.6 Time histories of wave height

2.3 三维带隔板液舱晃荡

本节将MPS 方法扩展到带垂直隔板的三维液舱晃荡问题计算中。液舱长度和高度与2.2 节中的二维液舱相同，在深度方向为0.6 m。舱内水深为0.2 m，隔板高为h =0.15 m，隔板位于自由面处，距离液舱底部0.5 m，隔板厚为0.006 m，距离左侧舱壁0.275 m。与2.2 节二维算例相似，液舱做受迫纵荡运动。运动幅值a=0.03 m，激励频率为ω =6.582 rad/s，该频率等于液舱一阶共振频率。

图7 三维带隔板晃荡流动瞬间Fig.7 Snapshots of sloshing in 3D baffled tank

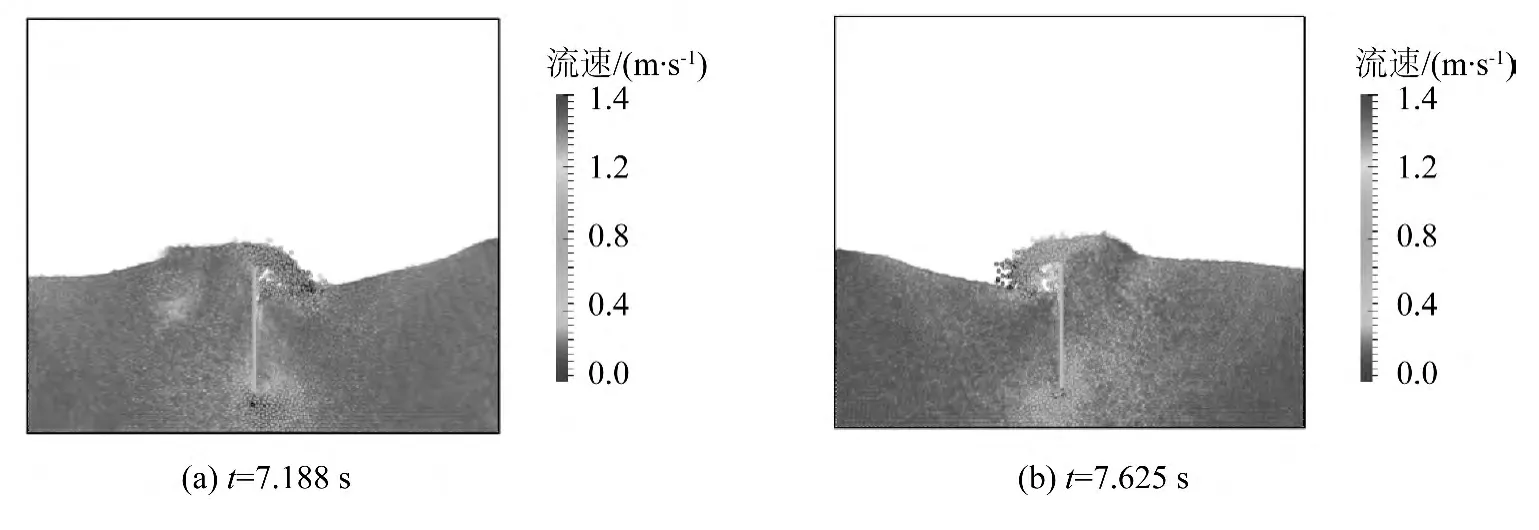
图8 隔板附近的速度Fig.8 Velocity around baffle

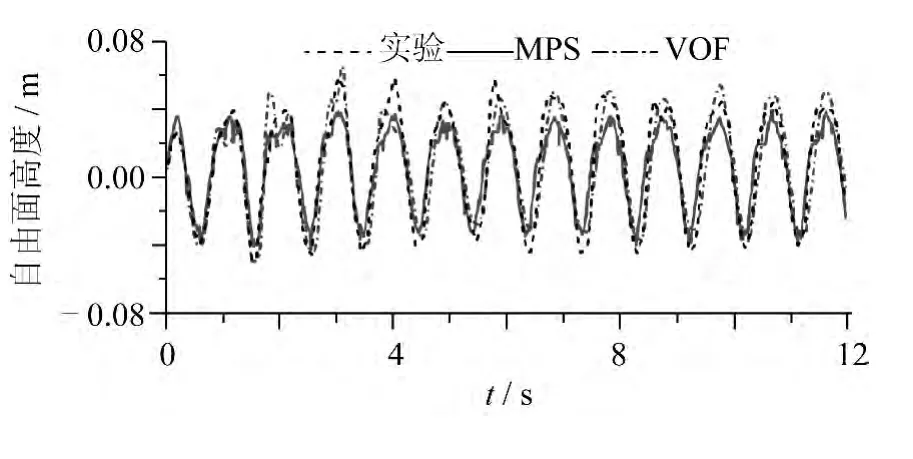
图9 三维带隔板液舱晃荡的自由面高度Fig.9 Wave height evolution in 3D baffled tank

计算使用的粒子总数为376 695，其中流体粒子数为274 195，其他为边界粒子。对应粒子间距为0.005 m，因此隔板的三维表达存在微小差别。图7给出了数值计算得到的流动瞬间，可以看到隔板的存在阻碍了自由面附近的液体运动，隔板两侧水面高度有较大差别，因此当流体流过隔板时发生了自由面的破碎，同时伴随着液体的飞溅。从图8 中也可以看到隔板附近的流动速度变化较大。图9 显示了波高监测点处水面高度随时间变化历程的实验和数值结果对比。计算结果能够与实验数据较好地吻合，但在峰值处存在一定的偏差，这主要是由于该三维算例中粒子间距较大，影响了自由面的捕捉精度，但压力的整体变化趋势与实验相一致。

3 结 语

文中将移动粒子法(MPS)应用于液舱晃荡问题计算，对二维液舱在纵荡运动时的晃荡进行了模拟，将计算得到的拍击压力与实验做了对比，结果表明:MPS 方法能够很好地模拟晃荡中的拍击现象。同时，对二维和三维带隔板的液舱晃荡进行了计算，结果显示隔板附近出现了波面的破碎和融合现象，采用MPS 方法能够较好地模拟这些复杂的流动现象。此处对比了数值计算得到的和实验测得的波高，二者吻合较好，表明MPS 方法能够较好地模拟带隔板的液舱晃荡问题。

［1］Lal A，Elangovan M.CFD simulation and validation of flap type wave-maker［J］.World Academy of Sciences，Engineering and Technology，2008，46:76-82.

［2］Nomura K，Koshizuka S，Oka Y，et al.Numerical analysis of droplet breakup behavior using particle method［J］.Journal of Nuclear Science and Technology，2001，38(12):1057-1064.

［3］Faltinsen O M.A numerical nonlinear method of sloshing in tanks with two-dimensional flow［J］.Journal of Ship Research，1978，22(3):193-202.

［4］Wu G X，Ma Q W，Eatock T R.Numerical simulation of sloshing waves in a 3D tank based on a finite element method［J］.Applied Ocean Research，1998，20(6):337-355.

［5］Frandsen J B.Sloshing motions in excited tanks［J］.Journal of Computational Physics，2004，196(1):53-87.

［6］Chen Y G，Djidjeli K，Price W G.Numerical simulation of liquid sloshing phenomena in partially filled containers［J］.Computers ＆ Fluids，2009，38(4):830-842.

［7］Liu D，Lin P.A numerical study of three-dimensional liquid sloshing in tanks［J］.Journal of Computational Physics，2008，227(8):3921-3939.

［8］Hu C，Kashiwagi M，Kishev Z.Numerical simulation of violent sloshing by CIP method［C］//Proceedings of 19th International Workshop on Water Waves and Floating Bodies.Cortona:［s.n.］，2004.

［9］郭晓宇，王本龙，刘 桦.低充水液舱晃荡气垫效应的数值分析［J］.水动力学研究与进展:A 辑，2011，26(5):623-630.(GUO Xiao-yu，WANG Ben-long，LIU Hua.Numerical investigation of air cushion effects on low filling sloshing impacts［J］.Journal of Hdyrodynamics，Ser.A，2011，26(5):623-630.(in Chinese))

［10］Lucy L B.A numerical approach to the testing of the fission hypothesis［J］.The Astronomical Journal，1977，82(12):1013-1024.

［11］Gingold R A，Monaghan J J.Smoothed particle hydrodynamics -Theory and application to non-spherical stars［J］.Royal Astronomical Society，1977，181:375-389.

［12］Koshizuka S，Oka Y，Tamako H.A particle method for calculating splashing of incompressible viscous fluid［C］//International Conference，Mathematics and Computations，Reactor Physics and Environmental Analyses.Portland:［s.n.］，1995.

［13］Koshizuka S，Oka Y.Moving-particle semi-implicit method for fragmentation of incompressible fluid［J］.Nuclear Science and Engineering，1996，123(3):421-434.

［14］张 驰，张雨新，万德成.SPH 方法和MPS 方法模拟溃坝问题的比较分析［J］.水动力学研究与进展:A 辑，2011，26(6):736-746.(ZHANG Chi，ZHANG Yu-xin，WAN De-cheng.Comparative study of SPH and MPS methods for numerical simulations of dam breaking problems［J］.Journal of Hydrodynamics，Ser.A，2011，26(6):736-746.(in Chinese))

［15］Delorme L，Colagrossi A，Souto-Iglesias A，et al.A set of canonical problems in sloshing，Part I:Pressure field in forced roll-comparison between experimental results and SPH［J］.Ocean Engineering，2009，36(2):168-178.

［16］Colagrossi Andrea，Landrini Maurizio.Numerical simulation of interfacial flows by smoothed particle hydrodynamics［J］.Journal of Computational Physics，2003，191(2):448-475.

［17］Colagrossi A，Lugni C，Brocchini M.A study of violent sloshing wave impacts using an improved SPH method［J］.Journal of Hydraulic Research，2010，48(S1):94-104.

［18］Khayyer A，Gotoh H.A higher order Laplacian model for enhancement and stabilization of pressure calculation by the MPS method［J］.Applied Ocean Research，2010，32(1):124-131.

［19］Lee B H，Park J C，Kim M H，et al.Step-by-step improvement of MPS method in simulating violent free-surface motions and impact-loads［J］.Computer Methods in Applied Mechanics and Engineering，2011，200(9-12):1113-1125.

［20］崔 岩，吴 卫，龚 凯，等.二维矩形水槽晃荡过程的SPH 方法模拟［J］.水动力学研究与进展:A 辑，2008，23(6):618-624.(CUI Yan，WU Wei，GONG Kai，et al.Numerical simulation of sloshing in two dimensional rectangular tanks with SPH［J］.Journal of Hydrodynamics，Ser.A，2008，23(6):618-624.(in Chinese))

［21］陈正云，朱仁庆，祁江涛.基于SPH 法的二维液体大幅晃荡数值模拟［J］.船海工程，2008，37(2):44-47.(CHEN Zheng-yun，ZHU Ren-qing，QI Jiang-tao.Simulations of 2D violent liquid sloshing based on SPH［J］.Ship ＆ Ocean Engineering，2008，37(2):44-47.(in Chinese))

［22］潘徐杰，张怀新.用移动粒子半隐式法模拟液舱横摇晃荡现象［J］.上海交通大学学报，2008，273(11):1904-1907.(PAN Xu-jie，ZHANG Huai-xin.Moving-particle semi-implicit method for simulation of liquid sloshing on roll motion［J］.Journal of Shanghai Jiao Tong University，2008，273(11):1904-1907.(in Chinese))

［23］潘徐杰，张怀新.移动粒子半隐式法晃荡模拟中的压力震荡现象研究［J］.水动力学研究与进展:A 辑，2008，23(4):453-463.(PAN Xu-jie，ZHANG Huai-xin.A study on the oscillations appearing in pressure calculation for sloshing simulation by using moving-particle semi-implicit method［J］.Journal of Hydrodynamics，Ser.A，2008，23(4):453-463.(in Chinese))

［24］Sueyoshi M，Naito S.A study of nonlinear fluid phenomena with particle method (Part 2):Two dimensional hydrodynamics forces［J］.Journal of Kansai Society of Naval Architects，2001，235:125-132.

［25］Hibi S，Yabushita K.A study on reduction of unusual pressure fluctuation of MPS method［J］.Journal of Kansai Society Naval Architects，2004，241:125-131.

［26］Khayyer A，Gotoh H.Modified moving particle semi-implicit methods for the prediction of 2D wave impact pressure［J］.Coastal Engineering，2009，56(4):419-440.

［27］Tanaka M，Masunaga T.Stabilization and smoothing of pressure in MPS method by Quasi-Compressibility［J］.Journal of Computational Physics，2010，229(11):4279-4290.

［28］Ataie-Ashtiani B，Farhadi L.A stable moving-particle semi-implicit method for free surface flows［J］.Fluid Dynamics Research，2006，38(4):241-256.

［29］Zhang Y X，Wan D C.Apply MPS method to simulate motion of floating body interacting with solitary wave［C］// Proceedings of the Seventh International Workshop on Ship Hydrodynamics.Shanghai:［s.n.］，2011:275-279.

［30］张雨新，万德成.MPS 方法在三维溃坝问题中的应用［J］.中国科学:物理学 力学 天文学，2011，41(2):140-154.(ZHANG Yu-xin，WAN De-cheng.Application of MPS in 3D dam breaking flows［J］.Sci Sin Phys Mech Astron，2011，41(2):140-154.(in Chinese))

［31］张雨新，万德成.用MPS 方法数值模拟低充水液舱的晃荡［J］.水动力学研究与进展:A 辑，2012，27(1):100-107.(ZHANG Yu-xin，WAN De-cheng.Numerical simulation of liquid sloshing in low-filling tank by MPS［J］.Journal of Hydrodynamics，Ser.A，2012，27(1):100-107.(in Chinese))

［32］Koshizuka S，Nobe A，Oka Y.Numerical analysis of breaking waves using the moving particle semi-implicit method［J］.International Journal for Numerical Methods in Fluids，1998，26(7):751-769.

［33］张雨新，万德成.改进的MPS 方法在晃荡问题中的应用［C］//第二十三届全国水动力学研讨会暨第十届全国水动力学学术会议文集.西安:［s.n.］，2011:156-163.(ZHANG Yu-xin，WAN De-cheng.Application of improved MPS in sloshing problem［C］// Proceeding of 23rd Chinese National Conference on Hydrodynamics.Xi’an:［s.n.］，2011:156-163 (in Chinese))

［34］Xue M，Lin P.Numerical study of ring baffle effects on reducing violent liquid sloshing［J］.Computers ＆ Fluids，2011，52:116-129.