圆盘剪刀轴有限元分析及优化设计
2014-11-22俞科斌李郝林陈吉勇
俞科斌, 李郝林, 陈吉勇
(1.上海理工大学 机械工程学院,上海 200093;2.上海宝菱冶金设备工程技术公司,上海 201900)
随着汽车、家电产业的快速发展,汽车用板和家电用板的剪切质量要求不断提高,尤其是汽车板材,不仅强度高,其剪切精度要求也不断提高,这对圆盘剪的切边质量及其设备性能提出了更高的要求.当前,圆盘剪的主要结构形式为悬臂式,在剪切厚板或高强度钢板时,剪切力明显增大,要求圆盘剪刀轴具有足够的强度、刚度,以确保高精度剪切来满足产品质量要求.
根据某厂一套圆盘剪设备的实际工作参数,建立圆盘剪刀轴和相关零部件的三维模型,对其进行仿真分析,通过理论公式计算与有限元力学分析,研究刀轴变形对圆盘剪刀片的重叠量和侧隙的影响,再利用Ansys Workbench软件中的实验数据法对刀轴进行优化设计分析,提出更加理想的设计方案.
1 圆盘剪技术参数
本圆盘剪是一套双刀头可旋转式的被动剪,其基本结构由固定底座、宽度调整装置、机架回转装置 及圆盘剪本体等组成,如图1所示.
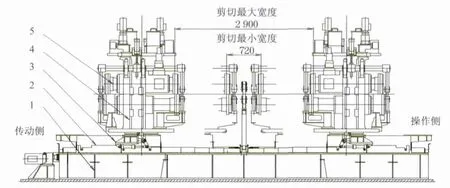
1.固定底座 2.宽度调整装置 3.机架回转装置 4.本体 5.刀轴
圆盘剪的核心部件为圆盘剪本体,主要由本体机架、刀轴、刀盘、重叠量调整装置和侧向间隙调整装置等构成[1].刀轴的三维模型如图2所示.

图2 上、下刀轴三维模型Fig.2 3D modle of top and bottom knife shaft
现介绍圆盘剪主要技术参数.
带钢规格.材质:普通冷轧钢板和高强度钢板;宽度:900~1 300mm;厚度:2~5 mm;抗拉强度:≤900 MPa;屈服强度:≤700 MPa;剪切速度:≤2m/s;切边宽度:5~50 mm;机架打开宽度:750~2 900 mm;刀盘直径:380~430 mm(其中,430mm为新刀直径,380mm 为磨损后最小可用直径);刀盘厚度:20~30mm(其中,30mm 为新刀厚度,20mm 为磨损后最小可用厚度);刀片重叠量调节范围:-25~+20mm(上刀片),-20~+25mm(下刀片);刀片侧向间隙调节范围:-7~+3 mm(上刀轴移动,下刀轴固定).
2 刀轴受力分析与计算
对圆盘剪刀轴的分析,首先考虑刀轴的强度、刚度是否满足工作要求,其次分析其受载荷后的变形情况,因为,刀轴的变形会直接影响圆盘剪刀片的重叠量以及侧向间隙的变化.当这些参数处于不合理的数值时,会使得剪切力明显增大,设备载荷增加,引起相关零部件的应力、应变增加以及零件变形、磨损加剧,带钢剪切质量下降,导致产品达不到规定要求.
根据材料力学理论,可将刀轴受力情况简化为简支梁模型,受力简图如图3所示.
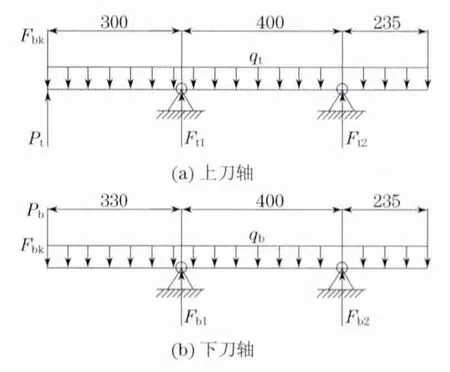
图3 刀轴受力简图Fig.3 Force diagram of knife shaft
在图3 中,Pt,Pb分别为上、下刀轴所受剪切力,大小相等,方向相反;Ftk,Fbk分别是上、下刀盘的重力;Ft1、Ft2为前后轴承对上刀轴的支撑力;Fb1,Fb2为前、后轴承对下刀轴的支撑力;qt,qb是上、下刀轴自身重力,以均布载荷的形式分布.
2.1 剪切力理论计算
根据圆盘剪实际尺寸参数和工作情况,采用村川正夫、前田桢三公式[2]计算剪切力F.
当刀片重叠量S≥0时,

式中,R 为刀片半径,R=215mm;S 为刀片重叠量,取S=0.45 mm;h′为带钢厚度,厚度范围2~3 mm,取h′=3 mm;σB为带钢强度极限,取σB=700 MPa;k1为刀片磨钝影响系数,一般取k1=0.8;k2为应力转化系数,一般取k2=0.75;计算得出剪切力F=21 500 N.
2.2 刀轴的挠度计算
圆盘剪刀轴主要约束为前、后两处轴颈的轴承约束,载荷为轴端安装刀盘处的剪切力作用.根据材料力学理论,将刀轴受载情况简化为简支梁模型[3].挠度
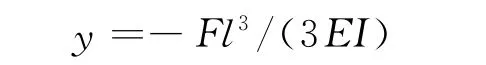
式中,l为剪切力作用点与轴承支撑点的轴向距离;E 为弹性模量,取E=210GPa;I 为刀轴的极惯性矩,I=1.47×108mm4.
计算得到上刀轴挠度为6.27×10-3mm,方向向上;下刀轴挠度为8.34×10-3mm,方向向下.
加工原料由湖北天越牧业有限公司从荆门当地采购收贮,玉米、豆粕、小麦麸、秸秆(主要为:玉米秸秆水分10%)、花生藤(水分9.7%)。
因此,在圆盘剪剪切过程中,上刀轴向上挠曲0.006 3mm,下刀轴向下挠曲0.008 3mm.上、下刀轴挠曲变形叠加后,由此引起圆盘剪刀片重叠量减小约0.014 7mm.从而可知,刀轴受力后引起的挠曲对刀片重叠量有一定的影响.
2.3 刀轴的转角计算
刀轴产生挠度表明刀轴轴端在径向发生了位移,而通过计算转角就可以推出刀轴在轴向发生的位移.转角
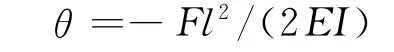
通过计算得到上刀轴的转角为3.13×10-5rad,下刀轴的转角为3.79×10-5rad.由此推出,上刀轴产生的转角导致上刀刃剪切点的轴向位移为-0.003 6mm,下刀轴产生的转角导致下刀刃剪切点的轴向位移为-0.004 4 mm.上、下刀刃位移叠加后,引起圆盘剪刀片侧向间隙增大0.000 8mm.因刀片侧向间隙的实际设定值为0.22mm,侧隙变化量相对较小,故可忽略不计.
3 刀轴有限元分析
3.1 建立三维模型
现以上刀轴为例,利用Ansys Workbench进行有限元力学分析.在有限元分析前,先根据刀轴实际尺寸建立三维模型.为便于分析计算,对刀轴的部分细节进行合理简化.选择刀轴材料为合金结构钢,同时设置好材料属性,主要参数:密度ρ=7 850kg/m3,弹性模量E=210GPa,泊松比μ=0.3.
3.2 网格划分
为得到精确的有限元分析结果,关键之一就是选择合理的网格划分方法.在Ansys Workbench中提供了多种网格划分方法,如自动划分法、四面体划分法、六面体主导法、扫掠划分法和多区划分法[4].经过多次调试,选择多区划分法,并将网格尺寸控制参数设定为10mm 时,得到的分析结果较为理想、精确.上刀轴网格划分后模型如图4所示.

图4 刀轴网格划分Fig.4 Mesh modle of knife shaft
3.3 施加约束与载荷
刀轴的约束条件主要是在前后两处轴颈的轴承约束,在Ansys Workbench中,轴承对刀轴的约束可定义成Cylindrical Support,即圆柱面约束.刀轴上的载荷主要是剪切力,由于剪切力是通过刀盘间接地作用在刀轴上,其在轴端圆柱面上的作用力分布类似于轴承载荷.为此,可将剪切力对刀轴的作用方式定义成轴承载荷的形式,大小为21 500N.另外,在剪切过程中,刀轴一直处于旋转状态,故在其上施加一惯性载荷,即旋转,转速为3rad/s.
3.4 求解与分析
对刀轴的分析主要有两方面:一方面是分析刀轴的应力、应变分布情况,找出刀轴的薄弱环节,计算其强度能否满足要求;另一方面是分析刀轴受载荷后的变形程度,特别是轴端安装刀盘处的变形情况.当轴端在径向发生变形时,会使刀片沿径向产生位移,导致重叠量的变化;而在轴向发生变形时,则会影响刀片侧向间隙.当刀片重叠量和侧向间隙大小不合理时,剪切力就会显著增大,圆盘剪的载荷也就随之增加,切边质量就会下降,甚至出现毛边或剪不断的情况,因此,在分析树中添加刀轴等效应力、应变、总体变形以及轴端的径向、轴向变形等分析项目.
上刀轴的应力分析结果如图5所示.从应力分布云图中可看出,刀轴最大应力约为8.1MPa.最大应力出现在轴承安装处的轴肩附近以及刀轴轴端底部.从刀轴的强度方面考虑,其最大应力8.1 MPa远小于其材料屈服强度700 MPa,所以,刀轴满足强度要求.

图5 上刀轴应力分布云图Fig.5 Stress distribution of top knife shaft
上刀轴的总体变形分析结果如图6(a)所示.从变形分析云图中可以看出,刀轴的最大变形发生在轴端,最大变形量约为0.007 9mm.
由于圆盘剪刀盘安装在刀轴轴端,且最大变形也发生在轴端,因此,进一步分析刀轴轴端的变形情况.刀轴轴端轴向变形和径向变形分布如图6(b)和6(c)所示.
从图6(b)中可以看出,上刀轴轴端轴向最大变形发生在轴端底部,大小为0.003 0 mm,方向为x轴负方向.从图6(c)中可以看出,上刀轴轴端径向最大变形为0.007 5mm,方向为y 轴正方向.
同样,对下刀轴进行分析后得出,最大应力约为8.2 MPa,刀轴的最大变形也发生在轴端,最大变形量约为0.008 8mm.轴端轴向最大变形发生在轴端顶部,大小为0.003 3mm,方向为x 轴负方向.轴端径向最大变形大小为0.008 4mm,方向为y 轴负方向.
现对上、下刀轴综合分析.如果将刀盘视为刚体,不考虑其变形影响,则上刀轴轴端轴向位移为-0.003 0mm,转 换 到 上 刀 刃 剪 切 点 的 位 移 为-0.006 5mm;下 刀 轴 轴 端 轴 向 位 移 为-0.003 3mm,转 换 到 下 刀 刃 剪 切 点 的 位 移 为-0.007 1mm.所以,上、下刀刃剪切点位移叠加后,其变化量为0.000 6mm,即上、下剪刃间的侧向间隙增大了0.000 6mm,而刀片侧向间隙量实际设定值为0.22mm,侧向间隙变化量与设定值相差两个数量级.因此,刀轴的变形对刀片侧向间隙的影响很小.另一方面,上刀轴轴端径向最大位移+0.007 5mm ,下 刀 轴 轴 端 径 向 最 大 位 移-0.008 4mm 两 者 叠 加 后,其 变 化 值 为0.015 9mm,即刀片重叠量减小了0.015 9mm,而刀片重叠量实际设定值为0.45mm.因此,对刀片重叠量有一定的影响.

图6 上刀轴变形情况Fig.6 Deformation of top knife shaft
4 刀轴结构优化设计
通过对刀轴有限元力学分析和理论计算分析,比较两种分析得出基本一致的结论:原刀轴结构尺寸满足强度、刚度要求,上、下刀轴受力后最大变形都发生在轴端安装刀盘处,其变形对刀片侧向间隙的影响非常小,可忽略不计,而对刀片重叠量有一定的影响.为此,利用Ansys Workbench对刀轴进行结构优化设计.
在Ansys Workbench 中,可 以 利 用Design Explorer模块来进行产品性能的优化设计.通过对多个设计点的参数分析,并将这些设计点拟合成响应曲面或曲线,从而找出最佳设计点,实现优化设计.
4.1 参数设置
在Design Explorer中,主要有输入、输出和导出这3类参数.结合前面对刀轴有限元力学分析可知,刀轴的强度已满足要求,结构优化主要是为了进一步提高刚度,减小其受力变形,为此,将刀轴轴端外径和内径定义成改变其结构的输入参数,将刀轴的质量和最大总变形定义为目标输出参数.其中,原刀轴的轴端外径为200 mm,内径为100 mm.采用实验数据法,设置其它9个刀轴实验设计点,外径变化范围:190~240 mm,内径变化范围:60~100mm,并定义设计变量类型为连续变量.
4.2 分析优化结果
在Design Explorer中,以中心组合的实验设计方式[5],经过分析计算得出各设计点的求解结果如表1所示.其中,D 为轴端外径,d 为轴端内径,M 为刀轴质量,T 为刀轴最大总变形.从表1中可以看出,3号设计点的质量最小,但其变形最大;而4号设计点的变形最小,变形量为0.006mm,但质量较大.
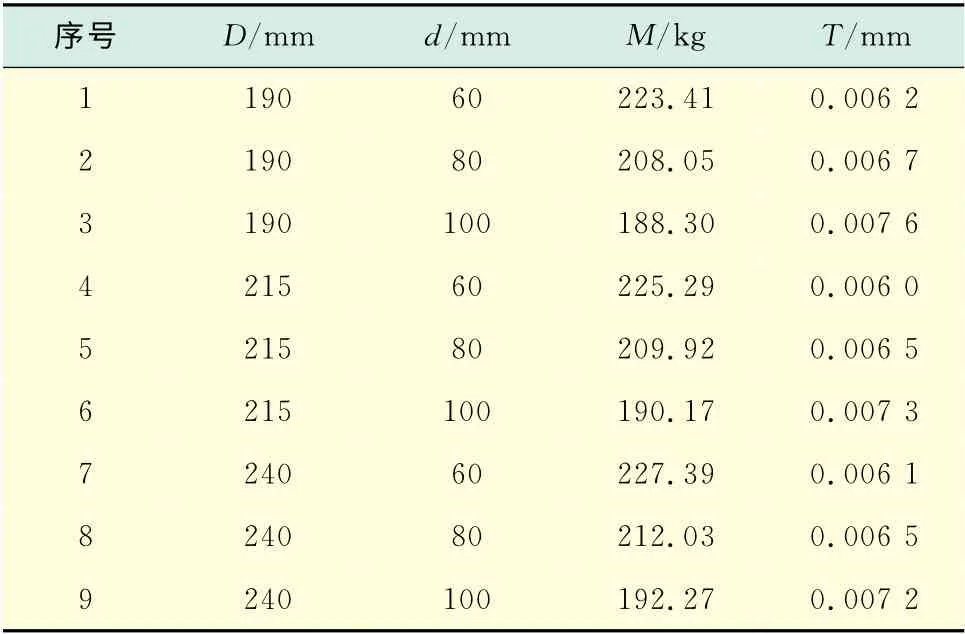
表1 设计点求解结果Tab.1 Solved result at design point
对表1设计点的求解结果进行分析得出:刀轴变形大致随轴端外径的增大而减小,随轴端内径的增大而增大;而刀轴质量与刀轴变形情况相反.图7为轴端外径与最大总变形关系曲线,从图7中可看出,刀轴变形的最小值出现在D=230mm 附近,因此,可将刀轴轴端外径定在230mm 较为合适.
刀轴内径、外径的选取会同时影响刀轴质量和变形.一方面,希望刀轴质量小,节省材料,降低成本;另一方面,希望刀轴变形小,避免影响刀片侧向间隙和重叠量等相关剪切参数.综合分析轴端内径、外径与刀轴质量以及刀轴最大总变形的关系,取刀轴内径为80mm、外径为230mm 时,刀轴的最大变形较小,且刀轴质量适中.
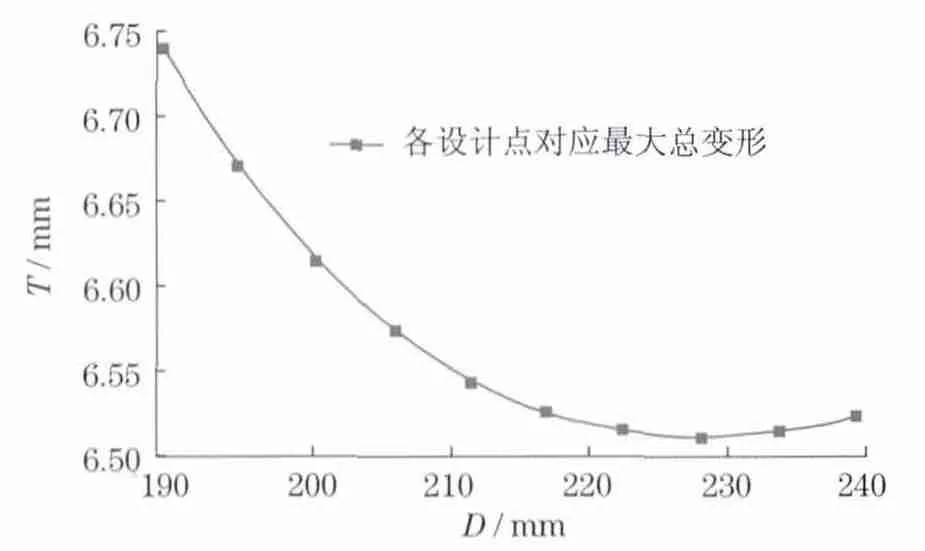
图7 刀轴外径与最大总变形关系曲线Fig.7 Curve of outer diameter vs maximum deformation
4.3 提出优化设计方案
通过以上分析,对原刀轴的部分尺寸进行修改,将轴端内径从初始的100mm 改为80mm,将轴端外径从初始的200mm 改为230mm.并以上刀轴为例,对优化后的刀轴进行再一次有限元力学分析,得出分析结果:刀轴最大应力为7.2 MPa(优化前,最大应力为8.1MPa),最大变形为0.006 5mm(优化前,最大变形为0.007 9mm),比原刀轴的应力分布和变形都有了改善.
5 结束语
通过理论计算分析和有限元力学分析这两种方法,对圆盘剪刀轴进行了强度、刚度的分析计算,找出了刀轴的薄弱环节.重点分析了刀轴轴端变形对刀片侧向间隙和重叠量的影响,并利用Ansys Workbench对刀轴进行优化分析、设计,提出更佳的设计方案.与理论计算相比,利用Ansys Workbench进行有限元分析更为直观、方便,不仅能快速得到刀轴的应力、应变分布和变形、位移情况,而且能够直观地找出刀轴的最薄弱环节,并能进行进一步结构优化设计,为以后的产品设计提供参考依据.
[1]邹家祥.轧钢机械[M].北京:冶金工业出版社,2000.
[2]刘培鄂.圆盘式剪切机剪切力计算[J].钢铁,1996,31(8):55-60.
[3]刘鸿文.材料力学[M].北京:高等教育出版社,2004.
[4]凌桂龙,丁金滨,温正.Ansys Workbench 13.0从入门到精通[M].北京:清华大学出版社,2012.
[5]李晓燕,王卫荣.压铸机合模机构的优化设计[J].上海理工大学学报,2000,22(2):175-179.
