偶图符号控制数的下界
2014-11-22徐保根
徐保根
(华东交通大学理学院,江西 南昌330013)
1 引言及定义
本文所指的图均为无向简单图,文中未说明的符号和术语同于文献[1-2]。
设G为一个图,用V(G)和E(G)分别表示G的顶点集和边集。对于任意顶点v∈V(G),定义v的邻域N(v)={u|uv∈E(G)},闭邻域N[v]=N(v)⋃{v}。dG(v)= ||N(v) 为v点在G中的度,并且Δ=Δ(G)和δ=δ(G)分别表示图G的最大度和最小度。若A和B为V(G)的两个不交子集,则
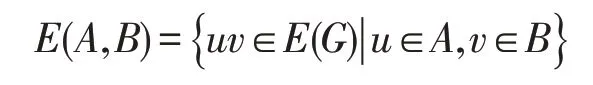
图的控制理论是图论中的重要课题,近些年来,图的控制概念有了许多新的变化,Cockayne E J等人[3]在符号控制的基础上,引入了多种控制概念和控制参数,这在一定程度上改变了人们对控制理论的认识。自从文献[4]中引入了图的符号边控制以来,各式各样的边控制概念和控制参数相继产生,使得控制理论在内容上不断丰富和完善,文献[5]中综述了近年来的主要研究成果。在文献[6-8]中,我们探讨了符号边控制的一些下界,并研究了偶图的符号边控制数。在本文中,将探讨偶图的符号控制数的下界。
为了方便,若S⊆V(G),f:V→R为一个实值函数,则记
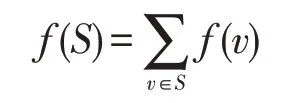
下面给出关于图的符号控制的定义。
定义1[3]设G=(V,E)是一个图,一个实值函数f:V→{- 1, +1} 满足f(N[u])≥1 对一切u∈V(G)都成立,则称f为图G的一个符号控制函数。图G的符号控制数定义为

且称满足γs(G)=f(V)的符号控制函数为G的一个最小符号控制函数。
2 主要结果及证明
本文主要给出偶图的符号控制数的两个下界,它们分别依赖于图的最大度和最小度。
定理1对于任意n阶偶图G,若Δ=Δ(G)表示图G的最大度,则有
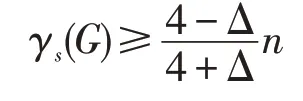
证明记G=(V,E),并且V=V1⋃V2为偶图G的2-部顶点划分,其中 ||Vi=ni(1 ≤i≤2),n1+n2=n。
设f为图G的一个最小符号控制函数,即有
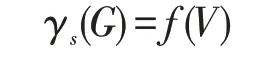
令A={v∈V|f(v)=+1} ,B={v∈V|f(v)=-1} ,|A|=s,|B|=n-s,显然有γs(G)=f(V)= |A|- |B|=2s-n。
记A1=A⋂V1,A2=A⋂V2,B1=B⋂V1,B2=B⋂V2。可见,V1=A1⋃B1,V2=A2⋃B2,并且A=A1⋃A2,B=B1⋃B2。
对于每个v∈B1,由定义知f(N[v])≥1,故v点至少与A中的两个点相邻,又因为G为偶图,即v点与A1中的点均不相邻,从而知v点至少与A2中的两个点相邻,故B1与A2之间的边数 |E(B1,A2) |≥2 |B1|。同理,B2与A1之间的边数 |E(B2,A1) |≥2 |B2|。
故A2中至少有一个点u,使得u点邻接B1中的点数不少于。由于f(N[u])≥1,且A2⊆V2为点独立集,故u点邻接A1中的点数也不少于
定理2对于任意n阶偶图G,若δ=δ(G)表示图G的最小度,则有
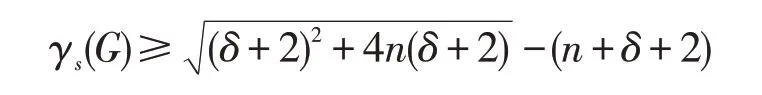
证明记偶图G=(V1⋃V2,E),其中V=V1⋃V2为偶图的二部点集划分。设f为图G的一个最小符号控制函数,即有γs(G)=f(V) 。与定理1 证明同样地,令A={v∈V|f(v)=+1} ,B={v∈V|f(v)=-1} ,|A|=s,|B|=n-s,显然有γs(G)=f(V)= |A|- |B|=2s-n。记A1=A⋂V1,A2=A⋂V2,B1=B⋂V1,B2=B⋂V2。可见,V1=A1⋃B1,V2=A2⋃B2,并且A=A1⋃A2,B=B1⋃B2。
对于对于每个v∈B1,由定义知f(N[v])≥1,注意到G为偶图,故v点至少与A2中个点相邻,即有。从而A2中存在一点u∈A2,使得u点与B1中至少个点相邻。又由定义知f(N[u])≥1,故u点与A1中至少个点相邻,即有,从而2 ||A1· ||A2≥ ||B2(δ+2),完全类似地也可得到2 ||A1· ||A2≥ ||B1(δ+2)。将两式相加得
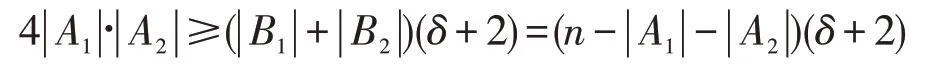
注意到
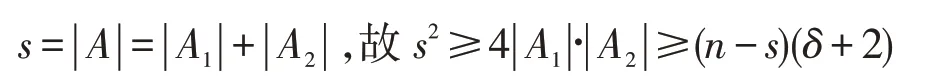
导出
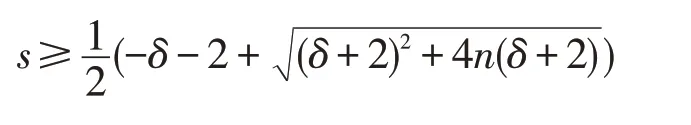
至此,定理2证毕。
[1] BONDYJ A,MURTY V S R.Graph Theory with Applications[M].Amsterdam:Elsevier,1976.
[2] HAYNES T W,HEDETNIEMI S T,SLATER P J.Domination in Graphs[M].New York:Marcel Dekker Inc,1998.
[3] COCKAYNE E J, MYNHARDT C M.On a generalization of signed dominating function of graphs[J].Ars Combin,1996,46:235-245.
[4] XU BAOGEN.On signed edge domination numbers of graphs[J].Discrete Math,2001,239:179-189.
[5] 徐保根.图的控制与染色理论[M].武汉:华中科技大学出版社,2013:11.
[6] 徐保根.关于图的符号边控制数的下界[J].华东交通大学学报,2004,21(1):110-113
[7] 徐保根.一类偶图的符号边控制数[J].华东交通大学学报,2004,21(2):124-126
[8] 赵金凤,徐保根.关于图的符号边控制数的下界[J].江西师大学报:自然科学版,2010,43(1):27-29.
