基于一元线性回归的可能性分布构造方法研究

李国平，杨风暴，吉琳娜，王肖霞

(1.中北大学 信息与通信工程学院，山西 太原030051 ;2.中北大学 理学院，山西 太原 030051)

0 引言

可能性理论是由美国著名控制论专家L.A.Zadeh 于1978年提出的，它可以描述模糊性和认知不确定性，以及能量化不确定性［1］.可能性分布是可能性理论中的一个重要概念，它在可能性理论中的作用如同概率分布在概率论中的作用一样.用可能性分布构造自然语言表示的命题和概念，从而可对它们进行定量分析.因此，可能性分布的构造会直接影响到可靠性分析，产品设计优化等的结果.可能性分布的构造方法文献中常见的是利用构造隶属函数的方法直接生成相应的可能性分布函数［2-3］，也有用概率/可能性相容原理利用概率分布转换为可能性分布［4-9］.文献［10］利用线性回归得到了梯形模糊数;文献［11］通过乘幂型分布构造了基于库水位的坝体安全等级的可能性分布;文献［12］介绍了基于可能性中值的可能性分布构造方法;文献［13］详细描述了三角形和梯形可能性分布的具体情况.

在实际问题中，由于许多可能性分布规律符合线性回归模型，且可能性分布一般描述一个自变量与因变量的对应关系，故本文基于一元线性回归构造可能性分布.若多个自变量同时影响因变量时，可将多元转化为一元来考虑，因为一元线性回归模型比多元线性回归模型更容易建立，且计算复杂度低，在实际问题中更具普适性.然而，并非所有变量之间的关系都是线性的，若问题中观测值的散点图大致呈某一曲线，又存在某种变换，可将该曲线转换成直线，就可以选择该变换将具有约束条件的非线性回归问题转换成线性回归问题［14］，从而利用线性回归的一些结果来解决这一问题.

1 基于一元线性回归的可能性分布构造

可能性分布的构造方法有很多，本文针对近似服从一条直线或曲线的一系列离散数据，通过一元线性回归构造这类数据的可能性分布.

回归分析就是建立变量间相关关系的具体的数学表达形式.在一元线性回归分析中，通常考虑两个变量:一个是自变量x，另一个是因变量y.对给定的x 值，y 值不能事先确定，故y 是随机变量，具有不确定性.

1.1 一元线性回归模型的参数估计及线性回归效果的显著性检验

假设y 与x 有如下的相关关系:

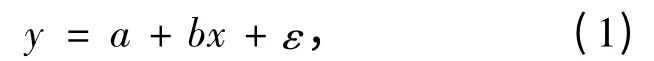
式中:a，b 为常数;ε 是一个随机变量且服从正态分布N(0，σ2)，即ε～N(0，σ2).

式(1)称为一元线性回归模型.当x 取固定数值时，y～N(a+bx，σ2)，y 的数学期望为E(y)=a+bx，回归方程为

称此方程为y 关于x 的回归直线方程，它反映出了E(y)随x 变化的规律.

这里，a 和b 的最小二乘估计为

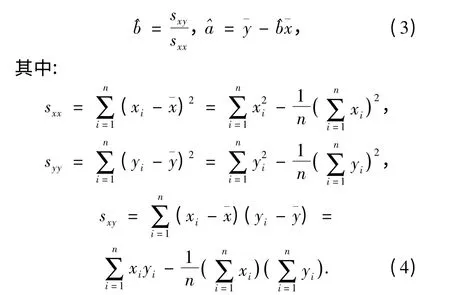
σ2的无偏估计量

在前面的讨论中，假设y 关于x 的回归为x的线性函数，然而在实际应用中还需通过实践来回答回归方程所描述变量之间关系的合理性，也可用统计方法对回归方程进行检验.常用的有t检验法，F 检验法和r 检验法，而且这三种检验的结果是完全一致的［14］.在实际的显著性检验中，任取一种加以应用即可.

1.2 几种常见的非线性模型及其线性化的方法

在实际问题中，有许多回归模型中的自变量和因变量的关系并非是线性的，但因变量或因变量的转换形式与某些未知参数的关系却是线性的，可通过适当的变量代换，将非线性模型转化为一元线性回归模型.几种常见的非线性模型及其线性化方法如表1 所示.

表1 几种常见的非线性模型及其线性化方法Tab.1 Several kinds of common nonlinear model and its linearization method

1.3 具体构造方法

基于一元线性回归的可能性分布构造的具体步骤如下:

1)根据实验或统计数据画出散点图.

2)根据散点图中散点的分布特点，从表1 几种模型中选出最佳模型.

3)利用最小二乘法估计最佳模型中的未知参数，进而求出回归方程.

4)利用上面提到的检验法对回归方程中的参数进行回归效果的显著性检验.

5)将回归方程转化为可能性分布函数.

2 实例分析

2.1 利用一元线性回归构造可能性分布实例分析

设论域X=［0，100］，在X 上定义一个“年老”的模糊集A，由于人们对“年老”的理解不一样，因此选择不同层次的人进行问卷调查.在说明“年老”的含义后，请他们填调查表.统计结果显示:不大于50 岁不是年老，大于70 岁人们才会认为是“年老”，而区间［51，70］则是年龄的一个过渡期［15］.人们认为“年老”的可能性程度如表2所示，试求“年老”的可能性分布函数.

表2 年龄［51-70］岁属于“年老”的可能性程度Tab.2 Possibility degrees of age［51-70］belonging to the“old”

由表2 所给的数据，可在二维直角坐标系中画出一个散点图，如图1 所示.

图1 年龄［51-70］岁属于“年老”的可能性程度散点图Fig.1 Scatter plot of possibility degrees of age［51-70］belonging to the“old”

由散点图可以看出，数据观测点大致分布在一条直线附近，并围绕直线上下波动，具有不确定性，这表明y 与x 之间存在一种线性关系.为此，可设由此可以建立y 对 x 的经验回归直线方程=-2.524 3 +0.050 4x.实际上，所谓经验回归直线方程，就是一条在最小二乘意义下拟合这些观测数据的最优直线.图1 给出了原始数据的散点所拟合的直线.

下面用t 检验法检验上例中的回归效果是否显著(取α=0.05).

在α=0.05 下，检验假设

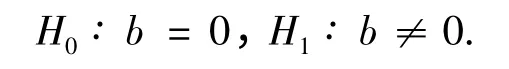
检验统计量为

拒绝域为

这里

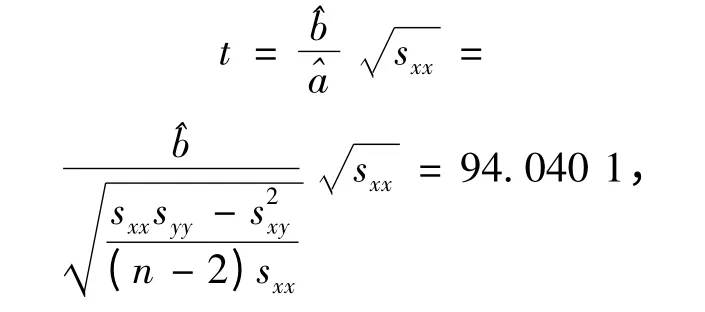
所以，拒绝H0∶b=0，接受H1∶b ≠0，即认为回归效果是显著的.从而“年老”的可能性分布函数为

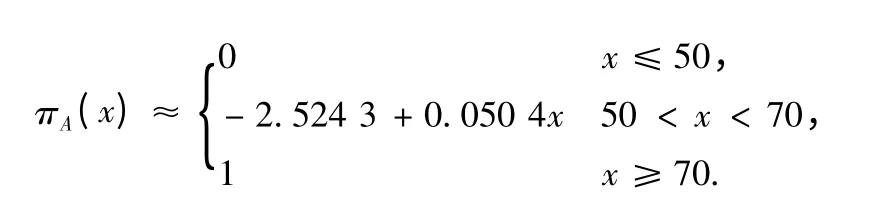
式中:x 表示年龄且为自然数.

本例也可用F 检验法，r 检验法对回归效果进行显著性检验.通过计算，检验结果完全一致.

2.2 可化为一元线性回归构造可能性分布的实例分析

以上讨论了一元线性回归的问题，在实际中常会遇到更为复杂的回归问题，在某些情况下，可通过适当的变量来变换，将它化成一元线性回归处理，下面举例说明.

设论域U={打火机}，试用模糊统计试验建立A=“优质打火机”的可能性分布函数.由于全国各地工厂的生产规模、生产水平和技术高低不同，人们对模糊概念“优质”的理解也不同，一般认为打火机打火500 次就算质量好了.作者向来自全国各地各阶层的150 人进行了问卷调查，在说明优质打火机的含义以后，请他们填写表3.在收回询问表后作出统计，结果如表4 所示.

表3 “优质打火机”含义的调查表Tab.3 Questionnaire of the meaning of“high quality lighter”

表4 150 人对于“优质打火机”含义的统计Tab.4 The statistics of the meaning of“high quality lighter”for 150 persons

按表4 的累计频率可以作出A(优质打火机)的可能性分布函数的散点图，如图2 所示.由图2可以看出，πA(x)随x 的变化呈现对数规律，因此选择对数模型πA(x)=a+bln x(b ＞0).令z=πA(x)，t=ln x，则有z=a+bt，按表4 给出的数据，计算得到表5.

表5 对数模型变换后的对应值Tab.5 Corresponding values after logarithm model transformation

图2 “优质打火机”的可能性分布散点图Fig.2 Scatter plot of possibility distribution of“high quality lighter”

由表5 通过计算可得

因此线性回归方程为

下面在显著性水平α=0.05 下检验假设H0∶b=0，H1∶b ≠0.采用r 检验法进行检验，现在n=15，n -2=13，查相关系数临界值表［14］，可得c=0.514，观测值r=0.997 5，|r|=0.997 5 ＞0.514，所以拒绝H0∶b=0，即认为z 关于t 的线性回归效果是显著的.将z=πA(x)，t=ln x 代入=-2.267 2 +0.489 0t中，得到

把这条曲线画在图3 中，可见基本上反映了πA(x)与x 之间的变化规律.

图3 “优质打火机”的可能性分布函数Fig.3 Possibility distribution function of“high quality lighter”

本例也可用F 检验法，t 检验法检验回归效果是否显著.通过计算，检验结果完全一致.

3 结论

构造可能性分布时，若变量间确实存在且在数量上表现为不确定性的相互依存关系时，就可以考虑利用回归分析这种统计方法来处理.通过回归效果的显著性检验，不但能够尽可能完整地描述信息的认知不确定性，而且能够尽可能贴切地对认知不确定性进行描述，减小其与真实分布的差异.此外，还可利用回归方程得到的可能性分布进行预测和控制.

［1］Zadeh L A.Fuzzy sets as a basis for a theory of possibility［J］.Fuzzy Sets and Systems，1978，l(1):3-28.

［2］周新宇.基于多源信息不确定性的可能性融合方法研究［D］.太原:中北大学，2012.

［3］侯艳华.认知不确定性条件下可能性分布的构造方法研究［D］.成都:电子科技大学，2010.

［4］佟欣.基于可能性理论的模糊可靠性设计［D］.大连:大连理工大学，2005.

［5］Serrurier M，Prade H.An informational distance for estimating the faithfulness of a possibility distribution，viewed as a family of probability distributions，with respect to data［J］.International Journal of Approximate Reasoning，2013，54:919-933.

［6］Masson M，Denoeux T.Inferring a possibility distribution from empirical data［J］.Fuzzy Sets and Systems，2006，157(3):247-254.

［7］Mauris G.Infering a possibility distribution from very few measurements［J］.ASC，2008，48:92-99.

［8］樊庆英，杨风暴，王肖霞，等.一种尾矿库风险评估的可能性处理方法［J］.计算机与现代化，2012(12):24-26.Fan Qingying，Yang Fengbao，Wang Xiaoxia，et al.Possibility processing method on tailings pond risk assessment［J］.Computer and Modernization，2012(12):24-26.(in Chinese)

［9］骆志高，何鑫，胥爱成，等.可能性理论在滚动轴承复合故障诊断中的应用［J］.振动与冲击，2011，30(1):73-76.Luo Zhigao，He Xin，Xu Aicheng，et al.Application of possibility theory in rolling bearing compound fault diagnosis［J］.Journal of Vibration and Shock，2011，30(1):73-76.(in Chinese)

［10］Garcia J M，Linares L J，Benitez L R，et al.Fuzzy numbers from raw discrete data using linear regression［J］.Information Sciences，2013，233:1-14.

［11］吉琳娜，杨风暴，王肖霞，等.基于库水位的坝体安全等级的可能性分析方法［J］.计算机工程与应用，2013，49(11):224-227.Ji Linna，Yang Fengbao，Wang Xiaoxia，et al.Possibility analysis method on safety levels of tailings dam based on reservoir water level［J］.Computer Engineering and Applications，2013，49(11):224-227.(in Chinese)

［12］何俐萍.基于可能性度量的机械系统可靠性分析和评价［D］.大连:大连理工大学，2010.

［13］Serrurier M，Prade H.An informational distance for estimating the faithfulness of a possibility distribution，viewed as a family of probability distributions，with respect to data［J］.International Journal of Approximate Reasoning，2013，54(7):919-933.

［14］赵颖.应用数理统计［M］.北京:北京理工大学出版社，2008.

［15］谢季坚.模糊数学方法及其应用［M］.武汉:华中科技大学出版社，2013.