基于遗传优化BP神经网络的供热管网故障诊断模型

段兰兰，田 琦，段鹏飞，李 哲

（太原理工大学 环境科学与工程学院，山西 太原 030024）

随着我国城市基础设施建设的不断完善，区域集中供热日益受到重视，供热管网的规模越来越大，系统也越来越复杂，供热管网的故障不断发生.供热管网故障中最常见的是泄漏故障，国内现有的供热管网普遍使用人工检漏和声学检漏来进行泄漏诊断［1］，容易受到人为和外界因素的干扰，误判率很高.

目前供热管网的故障诊断方法主要有：数学模型法，故障空间法和RC2法.一般管网的系统都很复杂，基于恒定流动模拟的静态和基于水力瞬态模拟的数学模型法［2］，很难达到数学模型规定的理想条件.故障空间法FDS（Fault Direction Space）［3］故障诊断方法能够比较准确地判断发生堵塞的管道，但是仅可判断出泄漏的大概方位；RC2方法［4］用于区域热力管网堵漏以及传感器故障诊断时准确性高，但是在工况变化不大时，易发生不收敛的情况.这些诊断方法都存在很大的局限性.

随着智能诊断技术的快速发展，采用BP人工神经网络进行供热管网泄漏故障诊断的研究不断增多［5］，但是BP 神经网络容易出现收敛速度慢，易陷入局部极值的问题［6］.本文通过将遗传算法［7-8］移植入传统BP 神经网络模型来对其进行优化，以避免其固有的不足，提出了一种基于遗传优化的BP神经网络供热管网泄漏故障诊断模型.该模型不仅可以快速、精确地诊断出发生泄漏的具体管段，还可以对泄漏点进行定位，并计算出泄漏量.

1 泄漏工况水力计算数学模型

1.1 模型假设

基于网络图论的相关知识，对热网的节点和管段进行编号，假设正常工况下热网有N个节点，B条有向管段，则可知热网有B-N+1个基本回路［9］.热网泄漏分为两种情况：①泄漏发生在节点处时，节点的净流出流量不再为0，节点的泄漏量即为此节点流量；②泄漏发生在管段时，网络拓扑关系发生变化，把泄漏点作为热网的一个新增节点，该节点把漏水管段分为两条管段，此时热网有N+1 个节点，B+1 条有向管段，B-N+1个基本回路.

1.2 计算模型

根据基尔霍夫流量定律，基尔霍夫压降定律［10］以及管段压力损失计算公式［11］，可得

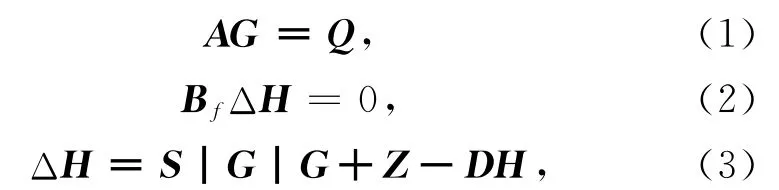
式中：A为热网的关联矩阵；G为管段流量列向量；Q为各节点（参考点除外）的净流出流量的列向量；Bf为热网的基本回路矩阵；ΔH为各条管段压降的列向量；S为B×B阶对角矩阵，其对角元素为各管段的阻力特性系数Si；｜G｜为B×B阶的管段绝对流量矩阵，其对角元素是向量G中各元素的绝对值；Z为各管段中两节点的位能差列向量（B维）；DH为管段水泵扬程列向量（B维），当管段不含水泵时，该管段DH＝0.

对矩阵A，G进行分块

式中：At为树支矩阵；Al为链支矩阵；Gt为树支流量向量；Gl为链支流量向量［10］.则式（1）变为

基于式（1）～（4）建立的热网泄漏工况数学模型，根据各管段阻力系数及水泵扬程等已知参数，可求解出各种泄漏工况下热网所有的管段流量及节点压力.本文利用节点方程法编程来求解热网泄漏工况的数学模型［12］，其计算流程如图1 所示.

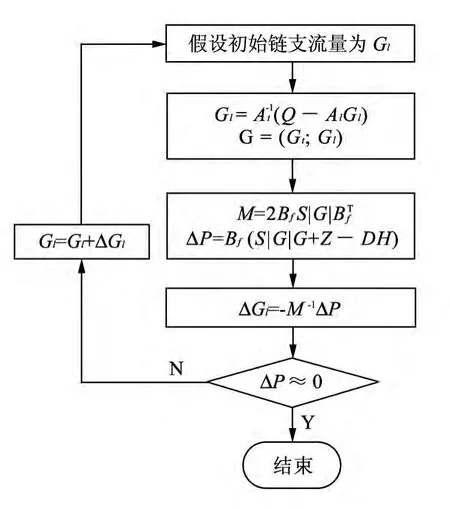
图1 节点方程法程序框图Fig.1 Node equation method program diagram

2 遗传优化BP 神经网络热网故障诊断模型

2.1 BP神经网络

BP（Back-Propagation）意为误差逆传播，BP神经网络是一种典型的多层前向网络，一般三层的BP神经网络就可以实现高度非线性映射［13］.BP 算法由两部分组成：①信息正向传播过程，输入信息从输入层经隐含层逐层计算传向输出层，得到每个单元的实际输出值.②信息反向传播过程，如果输出层未能得到期望的输出值，则计算输出值的误差变化值，根据此差值调节权值和阀值.不断重复这两个过程，当误差达到期望的要求时，网络的学习过程就结束.

虽然BP 神经网络已广泛应用于故障诊断方面，但其本身还是存在一定的限制和不足：①对于一些复杂问题，由于BP神经网络的学习速率是固定的，网络收敛速度慢，可能会需要较长的训练时间；②BP 算法采用的梯度下降法可以使网络收敛于某一值，但并不保证其为误差平面的全局最小值，很可能只是一个局部极小值.本文采用遗传算法来对传统BP 神经网络进行优化，以期解决前文提到的诸多不足和缺陷.遗传优化BP神经网络流程图如图2 所示.

图2 遗传优化BP 神经网络流程图Fig.2 Flow chart of BP neural network optimized by genetic algorithm

2.2 遗传优化BP 神经网络

遗传算法（Genetic Algorithms，GA）是一种通过模拟“适者生存，优胜劣汰”的自然进化过程来搜索全局最优解的方法.近年来我国有关遗传算法的理论和应用研究发展迅速［14-15］，遗传优化算法可以解决传统优化方法难以解决的非线性、全局寻优等复杂问题［16］.遗传算法的一般优化过程：把问题所存在的每个可能解编码成个体，随机产生一些个体的集合形成初始种群；计算初始种群中每个个体的适应度，根据适应度选择个体交叉（基因重组），所有个体按变异概率进行变异；经过选择、交叉、变异这三个操作产生下一代种群，如此循环直到满足优化准则为止.

在BP 神经网络进行训练学习之前，可以用遗传算法优化网络结构或优化网络的初始权值和阀值.由于优化网络结构比较困难，一般通过优化网络初始权值和阀值来提高BP 神经网络的精度和性能.

2.3 故障诊断模型建立

根据热网的系统结构及实际维护需要，热网故障诊断模型应分为两级：一级网络是热网泄漏管段的诊断，二级网络是具体泄漏点和泄漏量的诊断.本文一、二级故障诊断模型均采用最常用的三层结构BP神经网络模型.在网络训练学习之前，先利用遗传算法分别优化一、二级网络的初始权值和阀值，然后再进行BP网络训练学习直至收敛，得到诊断结果.

2.3.1 一级网络

一级网络的输入故障特征向量为热网节点的压力变化情况，输入层神经元数即为热网节点的个数（热网节点较多时可选取部分节点）；隐层节点数经多次反复试算后确定；输出故障特征向量为可能出现的故障类型，输出层神经元数为管段个数，输出层的激活函数为Sigmoid 函数，输出值在0～1 之间，代表此管段发生泄漏的概率.针对热网系统的特点，可以设定当输出值大于等于0.5 时认为此管段发生泄漏，输出值小于0.5 时认为此管段正常.

2.3.2 二级网络

针对热网每条管段分别建立一个BP 神经网络故障诊断模型，模型个数即为热网的管段数.输入故障特征向量和输入层神经元数与一级网络相同；隐层节点数经多次反复试算后确定；输出层有两个神经元，分别代表漏水位置和泄漏量.漏水位置为该漏水点距其所在管段起点的距离与此管段总长度的比值，泄漏量为泄水量与热网总循环水量的比值.

2.3.3 样本的采集

热网故障诊断的样本数据可以通过实测或者水力工况模拟来获取，但是因为各方面因素的限制，通过实测采集到合理的样本数据比较困难，一般通过热网泄漏工况水力计算数学模型模拟来获取样本数据.

为了方便数据处理，加快网络收敛速度，输入数据需要进行归一化处理，使其范围限制在［0，1］之间，防止由于输入值过大引起神经元输出饱和.一、二级网络样本输出数据都在［0，1］之间，不需要归一化处理.

3 故障诊断实验分析

实验选取如图3 所示的供热系统，系统共有4 个用户，13 条管段，10 个节点.假设热源和各用户的设计阻力损失均为105Pa，在正常工况下，热网循环水量为60m3／h，各用户的流量均为15m3／h，水泵扬程为3×105Pa.

图3 供热管网系统图Fig.3 Heating network system diagram

通过泄漏工况水力计算数学模型模拟来获取样本数据.首先对正常工况进行模拟，得到各节点的压力和管段流量；然后分别假设各条管段的不同位置的点泄漏.本文选取距其所在管段起点的距离与此管段总长度的比值为0（节点处泄漏），0.1，0.2，0.3，0.4，0.5，0.6，0.7，0.8，0.9的 点.假设各个泄漏点发生不同程度的泄漏，选取泄漏量分别为系统总循环量的1%，2%，3%，4%（事故补水泵一般取总循环水量的4%），此热网系统有13 条管段，模拟上述所有泄漏工况，就可得到520 组泄漏样本数据.

分别采用遗传优化BP 神经网络诊断模型和传统BP 神经网络模型进行故障诊断，并对两种模型的诊断结果进行对比分析.

3.1 一级网络故障诊断

随机选取全部样本的90% 作为训练样本，其余10% 为测试样本.网络拓扑结构为9-13-13，最大迭代次数为1 000，收敛精度为0.000 1.遗传算法参数设置：种群规模设定为30，交叉概率为0.3，变异概率为0.1，进化代数为20.通过遗传优化得到最优初始权值和阀值，并代入BP 网络，经32 次迭代后网络达到收敛，训练误差为0.004 65.同时建立一个相同结构的传统BP 网络，经116 次迭代后网络达到收敛，训练误差为0.005 74.上述两种网络得到的诊断结果如表1所示（由于篇幅限制，只列出了52 组测试样本中的5 组）.

表1 一级网络测试样本诊断结果Tab.1 Diagnosis results of one-level network＇s test samples

3.2 二级网络故障诊断

针对不同的管段把全部样本分为13 组（每组包含40 个样本），分别建立遗传优化BP 网络热网故障诊断模型.网络拓扑结构为9-9-2，最大迭代次数为1 000，收敛精度为0.000 01.遗传算法参数设置：种群规模设定为30，交叉概率为0.3，变异概率为0.1，进化代数为20.同时建立了13个相同结构的传统BP网络.每个二级故障诊断模型有4个测试样本，计算这4 个测试样本的实际输出和期望输出的平均相对误差.

3.3 诊断结果分析

3.3.1 一级网络诊断结果分析

由表1 数据分析可知，两种模型都能正确诊断出泄漏管段，但是遗传优化BP 神经网络诊断管段发生泄漏的概率比传统BP 神经网络更准确；对两种模型网络迭代次数和训练误差对比发现，经过遗传优化后的BP 神经网络的收敛次数从116 次减少了到32 次，收敛速度提高了72.4%；训练误差由0.005 74 降低到了0.004 65，误差精度提高了19.9%.此实验热网选取的系统结构较简单，实际热网系统往往都很复杂，对于复杂的系统对比结果会更明显.

3.3.2 二级网络诊断结果分析

二级网络两种模型的诊断误差曲线如图4，图5 所示，可以看出传统BP 神经网络的诊断误差较大，其中L7管段的泄漏位置和泄漏量的相对误差分别为10.08% 和11.76%，超出了误差允许范围；经过遗传算法优化的BP 神经网络泄漏位置和泄漏量的相对误差均小于传统BP 网络，且全部在0～10% 范围之内，诊断结果比较理想.

由计算可知，传统BP神经网络诊断模型泄漏位置和泄漏量的相对误差平均值分别为4.36%和5.72%，遗传优化BP 神经网络诊断模型泄漏位置和泄漏量的相对误差平均值分别为1.32%和2.84%，由此可知遗传优化提高了BP 神经网络故障诊断模型的诊断精度.

图4 泄漏位置相对误差图Fig.4 Relative tolerance of leakage location diagram

图5 泄漏量相对误差图Fig.5 Relative tolerance of leakage rate diagram

4 结论

上述实例计算结果的对比分析表明：一级网络诊断模型经遗传优化后，收敛速度提高了72.4%，误差精度提高了19.9%；二级网络诊断模型经遗传优化后，泄漏位置和泄漏量的相对误差平均值分别降低了3.04%和2.88%.可得出以下结论：

1）遗传算法优化可以解决BP 网络模型收敛速度慢、易陷入极小值的问题.

2）基于遗传优化BP 神经网络供热管网故障诊断模型的收敛速度和诊断能力均优于传统的BP 神经网络模型，可以有效地应用到供热管网故障智能诊断系统中.

［1］金富根.热网泄漏检测及控制方法［J］.煤气与热力，2008，28（2）：A11-A13.Jin Fugen.Leak detection and control methods of heat supply network［J］.Gas ＆ Heat，2008，28（2）：A11-A13.（in Chinese）

［2］杨开林，郭宗周.热力管网泄漏检测数学模型［J］.水利学报，1996，5（5）：50-56.Yang Kailin，Guo Zongzhou.Investigation of mathematical models for leak detection of heating distribution networks［J］.Journal of Hydraulic Engineering，1996，5（5）：50-56.（in Chinese）

［3］石兆玉，陈弘.故障空间（FDS）法在供热管网故障诊断中的应用［J］.区域供热，1994（3）：17-19.Shi Zhaoyu，Chen Hong.Application of fault direction space in heating network leakage fault diagnosis［J］.District Heating，1994（3）：17-19.（in Chinese）

［4］Jiang Yi，Qin Xuzhong.Hydraulic process fault diagnosis and parameter identification in district heating networks［J］.ASHRAE Trans，2000，106（II）：284-291.

［5］Lei Cuihong，Zou Pinghua.Application of neural network in heating network leakage fault diagnosis［J］.Journal of Southeast University（English Edition），2010，26（2）：173-176.

［6］Ding Shifei，Xu Xinzheng，Zhu Hong.Studies on optimization algorithms for some artificial neural networks based on genetic algo-rithm（GA）［J］.Journal of Computers，2011，6（5）：939-946.

［7］Booker L B，Goldberg D E，Holland J H.Classifier systems and genetic algorithm［J］.Artificial Intelligence，1989，40（1）：235-242.

［8］边霞，米良.遗传算法理论及其应用研究进展［J］.计算机应用研究，2010，27（7）：242-243.Bian Xia，Mi Liang.Development on genetic algorithm theory and its applications［J］.Application Research of Computers，2010，27（7）：242-243.（in Chinese）

［9］王思莹，邹平华，周志刚，等.基于图论的直接连接热水供热系统热力工况计算模型［J］.暖通空调，2011，41（8）：106-109.Wang Siying，Zou Pinghua，Zhou Zhigang，et al.Thermal condition calculation model of direct connection hot water heating system based on graph theory［J］.Heating Ventilating ＆ Air Conditioning，2011，41（8）：106-109.（in Chinese）

［10］孙巍.供热管网的建模分析以及水力平衡调节［D］.北京：北京化工大学，2008.

［11］王晓霞，邹平华.多热源环状空间热网拓扑结构研究［J］.暖通空调，2009，39（2）：1-4.Wang Xiaoxia，Zou Pinghua.Topological structure of multiheat source ring-shaped heat-supply network［J］.Heating Ventilating ＆ Air Conditioning，2009，39（2）：1-4.（in Chinese）

［12］王海，王海鹰，周海珠.多热源环状管网的面向对象水力计算方法［J］.浙江大学学报（工学版），2012，46（10）：1900-1909.Wang Hai，Wang Haiying，Zhou Haizhu.Analysis of multi-sources looped-pipe network based on object-oriented methodology［J］.Journal of Zhejiang University（Engineering Science），2012，46（10）：1900-1909.（in Chinese）

［13］田旭光，宋彤，刘宇新.结合遗传算法优化BP 神经网络的结构和参数［J］.计算机工程与软件，2004，21（6）：69-71.Tian Xuguang，Song Tong，Liu Yuxin.Optimizing the structure and parameters of BP neural network based on genetic algorithm［J］.Computer Applications and Software，2004，21（6）：69-71.（in Chinese）

［14］苑希明.神经网络和遗传算法在水科学领域的应用［M］.北京：中国水利水电出版社，2002.

［15］Ghidu K，Ahmed S.Automatic generation of objectoriented tests with a multistage-based genetic algorithm［J］.Journal of Computers，2010，5（10）：560-569.

［16］Whitely D，Starkwarther T.Genetic algorithms and neural networks：optimizing connections and connectivity［J］.Parallel Computation，2006，14（3）：347-361.