复Hilbert空间上的零伦全纯映照的构造
2014-11-22刘爱超程俊芳
刘爱超,程俊芳,刘 浩
(1.黄淮学院 数学系,河南 驻马店 463000;2.河南大学 数学与信息科学学院,河南 开封 475004)
在多复变数中,利用不同的Roper-Suffridge算子(各种形式及相应性质可参见文献[1-5])在高维空间中可以构造出多种星形映照、螺形映照及其扩充子族.零伦映照的概念由刘浩教授提出,其相关结果可参见文献[6-7].目前,零伦映照的研究成果并不多,仅可见文献[6-8].在拓扑学中同伦是映射间的连续变形,能否将Roper-Suffridge算子与拓扑学中同伦的概念相结合,构造出复高维空间中的零伦映照呢?作者在参照文献[5]与[6]的基础上,结合不同形式的Roper-Suffridge算子对零伦全纯映照进行了研究,并得出复平面中单位圆盘上的正规化零伦全纯函数可以分别构造出复Hilbert 空间单位球B和Ω(p2,…,pn+1)上的零伦映照.所得结论对复欧式空间Cn中的单位球Bn同样成立.
1 预备知识
记C为复平面,U为C中的单位圆盘,即U={z∈C∶|z|<1}.D是C中的域,H(D,D)表示从D到D的全纯函数的集合.H为一复Hilbert空间,<·,·>为其中的内积,对∀z∈H,记B={z∈H∶‖z‖ <1}为H中的开单位球.
用H(B)表示B⊂H到H的全纯映射的全体.若Df(z)(为f在z点的一阶Fre′chet导数)在每一点z∈B有有界逆,称f为B上的局部双全纯映射;若(DF(z))-1存在,且在f(B)上全纯,称f为B上的双全纯映射;若f∈H(B)满足f(0)=0,Df(0)=I(为单位矩阵),称f为B上正规化全纯映射.
设X和Y都是拓扑空间,记f,g∈C(X,Y)(C(X,Y)为从X到Y的所有连续映照构成的集合),所谓f与g同伦,就是指f可以“连续地”变为g,这意味着在每一时刻t∈T(T=[0,1])有一连续映射Gt∈C(X,Y),使得G0=f,G1=g,并且Gt对t有连续地依赖关系,即
若有连续映射G∶X×T→Y,使得对任意的x∈X,G(x,0)=f(x),G(x,1)=g(x),则称f与g同伦,简记为f≃g,并称G是连接f与g的一个同伦,记作G∶f≃g.
解析同伦的定义首先由刘浩教授给出,本文为了将Roper-Suffridge算子与拓扑学中同伦的概念相结合,将解析同伦定义中的条件减弱如下:
定义1 设X,Y是H中的域,称映照族{Gt}t∈T,Gt(z)=G(z,t)∶X×T→Y为一解析同伦,如果G(z,t)关于z全纯,关于t除去一零测度集外是C∞的.其中T=[0,1].
定义2 设f(z),g(z)是从X到Y的映照,称f与g解析同伦,如果存在一个解析同伦G(z,t)∶X×T→Y,使得G(z,0)=f(z),G(z,1)=g(z).简记为G∶f≃g,并称G是连接f与g的一个解析同伦.
定义3 设f(z)∈H(B),称f关于G零伦,如果f(B)上的恒等映照I解析同伦于f(B)上的零映照,即存在G(ω,t)∶f(B)×T→f(B),使得G(ω,0)=0,G(ω,1)=ω.
从几何上讲,f是零伦的相当于对f(B)中任一点f(z),连接f(z)与零点的光滑曲线G(f(z),t)完全落在f(B)之中.
从上述定义出发,将两种不同形式的Roper-Suffridge算子与零伦全纯映照结合起来进行研究,得出复平面中单位圆盘上的一个正规化零伦全纯函数可以分别构造出复Hilbert空间单位球B和Ω(p2,…,pn+1)上的一个零伦映照.
在全文证明过程中,所使用的各种复指数函数ζα=eαLnζ=eα[ln|ξ|+i(argζ+2kπ)]=eα[ln|ξ|+iargζ],ζ≠0,α为实常数,均取分支,令k=0.
2 主要结果与证明
在给出主要定理之前,首先给出以下两个引理(以下记T=[0,1]).
引理1[9]若f∈H(U,U),则,z∈U.
引理2[10]若f∈H(U,U),且f(0)=0,则|f(z)|≤|z|.
定理1X表示具有内积 <·,·> 的复Hilbert空间,B为X中的单位球.f∈H(U,U)为正规化双全纯函数,f关于g是零伦的,且g(ω,t)满足:
1)g(0,t)=0;
2)g(ω,t)=a1(t)ω+a2(t)ω2+…,a1(t)≠0.
令
则F在B上关于G零伦,其中β∈[0,1],γ∈,β+γ≤1,幂函数取分支,使得此处

取分支使得
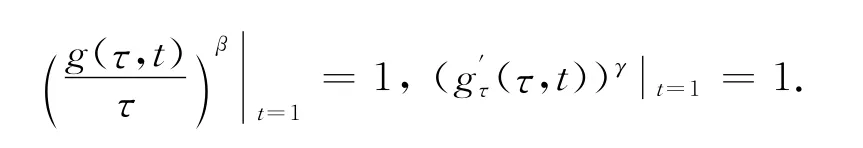
证明 由定义知G(ω,t)关于ω全纯,除t≠0 外是C∞的,即G(ω,t)是一个解析同伦;又f关 于g是零伦的,则g(ω1,0)=0,g(ω1,1)=ω1,易得G(ω,0)=0.
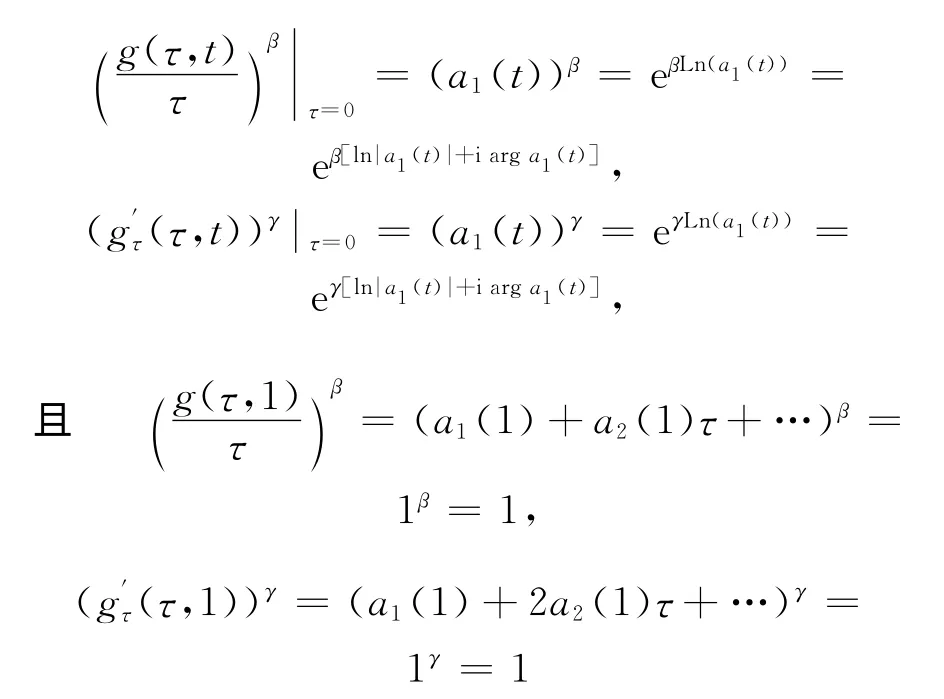
有意义,进而得G(ω,1)=ω.注意到
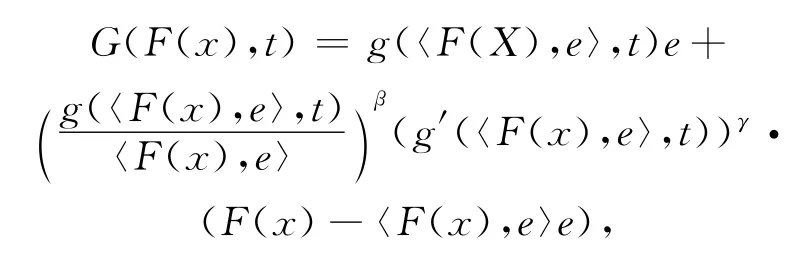
计算易知
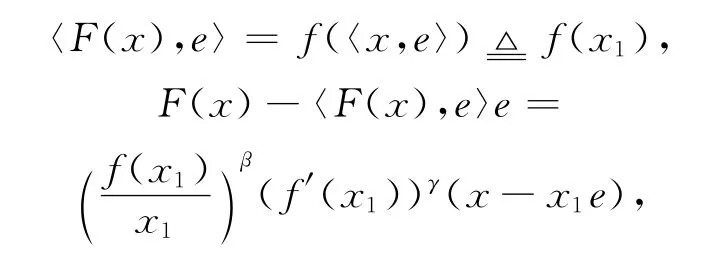
其中记〈x,e〉=x1,x-〈x,e〉e=x′.代入后有

由几何意义,只须对∀t∈T,x∈B,找到u∈B,使得连接0 与F(x)的曲线完全落在F(B)之中,即G(F(x),t)=F(u).当t=0 时,只须取u=0 即可.下面仅讨论t≠0 的情形.
因f关于g是零伦的,由定义知存在u1∈U,使得g(f(x1),t)=f(u1).令
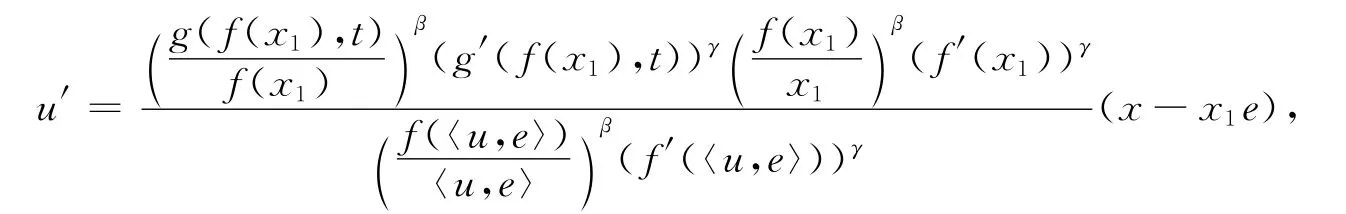
易得〈u′,e〉=0.记u=u′+u1e,则〈u,e〉=u1.于是
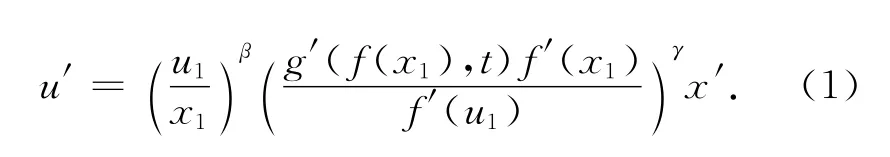
对g(f(x1),t)=f(u1(x1))两端关于x1求导,得),代入式(1)有

又u1(x1)=f-1(g(f(x1),t))∈H(U,U),u1(0)=0,由引理1 知,;由引理2 知,|u1|≤|x1|,且注意到2γ∈[0,1],于是
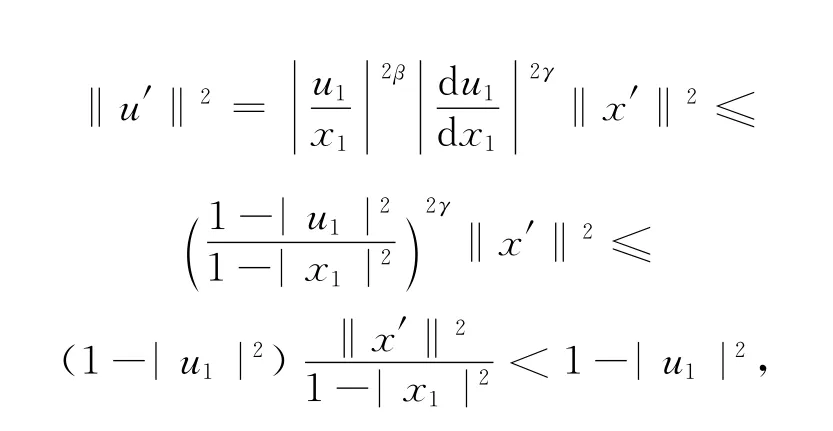
即u∈B,由定义知F在B上关于G是零伦的.
注记 当β=0,γ=0时,定理1分别有对应的形式,文中不再赘述.
下面将在更广泛的复Hilbert空间的域上讨论推广的Roper-Suffridge算子可以保持零伦的性质不变.下述定理2 中的域及Roper-Suffridge 算子来源于文献[11].记
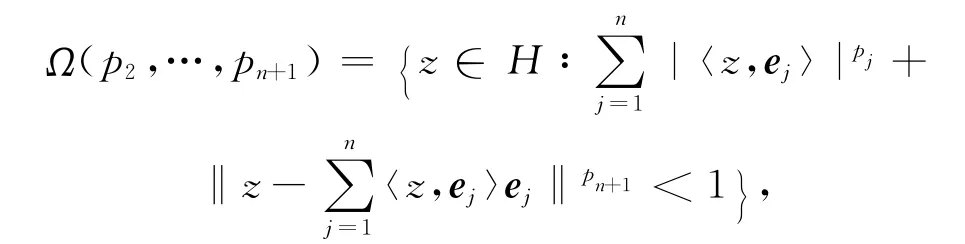
其中ej为H中相互正交的单位向量,pj>0(1≤j≤n+1).显然当pj=2 时,Ω(p2,…,pn+1)就是Hilbert空间中的单位球B.
定理2X表示具有内积〈·,·〉的复Hilbert空间,f∈H(U,U)为正规化双全纯函数,f关于g是零伦的,g(ω,t)∶f(U)×T→f(U)为一解析同伦,并且满足:

则F在Ω(p2,…,pn+1)上关于G是零伦的,其中
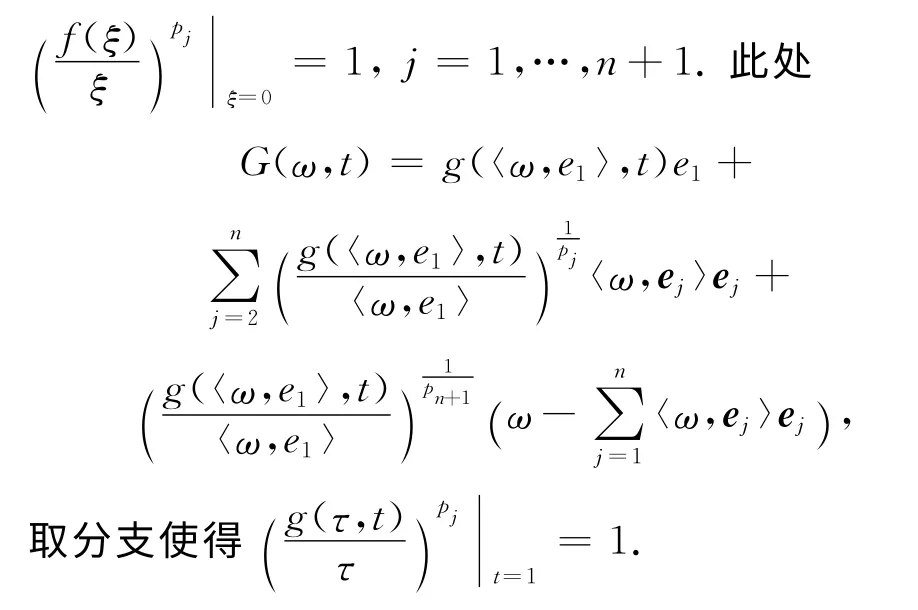
证明 同定理1 的证明,有G(ω,0)=0,G(ω,1)=ω,且

记〈x,e〉=x1,x-〈x,e〉e=x′,代入(2)后有

由几何意义,只须对∀t∈T,x∈Ω(p2,…,pn+1),找到u∈Ω(p2,…,pn+1),使得连接0 与F(x)的曲线完全落在F(Ω(p2,…,pn+1))之中,即G(F(x),t)=F(u).当t=0 时,只须取u=0 即可.下面仅讨论t≠0 的情形.
因f关于h是零伦的,则存在u1∈U,使得g(f(x1),t)=f(u1).令


因此
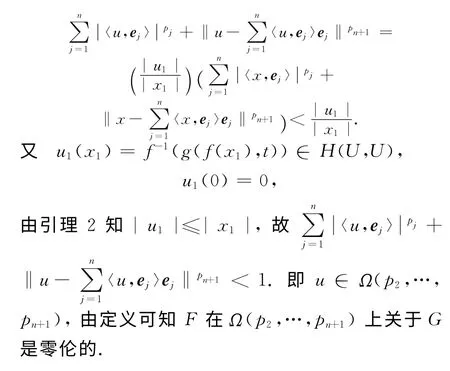
3 结论
近几年,冯淑霞带领其团队在Roper-Suffridge算子的性质上做了很多工作,本文在参考文献[5-6]的基础上,对解析同伦定义中的条件作了减弱,利用刘小松博士和刘太顺教授推广的Roper-Suffridge算子,得出复平面中单位圆盘上的正规化零伦全纯函数可以分别构造出复Hilbert空间单位球B和Ω(p2,…,pn+1)上的一个零伦映照.所得结论对复欧式空间Cn中的单位球Bn同样成立.
[1]Graham I,Kohr G.Lowner chains and the Roper-Suffridge extension operator[J].Journal of Mathematical Analysis and Applications,2000,247(2):448-465.
[2]Graham I,Kohr G.Univalent mappings associated with the Roper-Suffridge extension operator[J].Journal d’Analyse Mathématique,2000,81(1):331-342.
[3]Graham I,Hamada H,Kohr G,et al.Extension operator for locally univalent mappings[J].Michigan Mathematical Journal,2002,50(1):37-55.
[4]冯淑霞.多复变数的几类全纯映照族[D].合肥:中国科学与技术大学,2004.
[5]刘小松.多复变函数几何函数论中某些映照子族的性质[D].合肥:中国科学与技术大学,2004.
[6]崔艳艳.单位球上的零伦全纯映照[D].开封:河南大学,2006.
[7]杨红朝.多复变数的零伦全纯映照[D].开封:河南大学,2007.
[8]刘爱超.有界星形圆型域上的零伦全纯映照[J].数学的实践与认识,2013,43(17):247-254.Liu Aichao.Null-homotopic holomorphic mappings on the bounded starlike circular domains[J].Mathematics in Theory Ang Pratice,2013,43(17):247-254.(in Chinese)
[9]Ahlfors L V.Complex Analysis[M].New York:Mc Graw-Hill,1953.
[10]钟玉泉.复变函数论[M].北京:高等教育出版社,2008.
[11]陈慧勇.多复变数的抛物星形映射[D].开封:河南大学,2008.
