求解非奇异线性方程组的正交降阶法
2014-11-22李胜利王川龙温瑞萍
李胜利,王川龙,温瑞萍
(1.太原理工大学 数学学院,山西 太原 030024;2.工程科学计算山西省重点实验室,山西 太原 030012)
1 预备知识
线性方程组

是非奇异矩阵,其解法已有了广泛的研究,主要包括直接法[1-3]和迭代法[4-5].其中直接法包括高斯消去法,Gram-Schmidt正交化QR方法,双对角化方法等.单从浮点数(Flop Numbers)角度看,高斯消去法是解线性方程组(1)最经济的方法[1-2,6-7].但是高斯消去法数值稳定性较差[7],我们不得不考虑“增长因子”的影响.Gram-Schmidt正交化QR[3,8-11]与双对角化方法[6]对于病态问题更可靠,但是计算量又过大.本文提出的正交降阶方法既能保证较好的数值稳定性,又比Gram-Schmidt正交化QR以及双对角化方法所需计算量要少.
为方便,用Rn×n表示n阶实矩阵全体,Rn表示n维实向量全体,AT和xT分别表示矩阵A和向量x的转置,(x,y)表示向量x和向量y的内积.A=[v1,v2,…,vn]是A∈Rn×n的一个列划分,即vi=(a1,i,a2,i,…,an,i)T,i=1,2,…,n.
下面是本文将要用到的一个重要结果.
定理1 设A∈Rn×n为非奇异矩阵,将A的第1列中第1个不为零的元素记为ai,1,将A的后n-1 列分别与第1列正交后去掉第1列和第i行剩下的(n-1)×(n-1)矩阵仍然非奇异.
证明 设A的各列向量分别记为v1,v2,…,vn-1,vn,现在将后n-1列分别和第1列正交化,用Gram-Schmidt正交化得

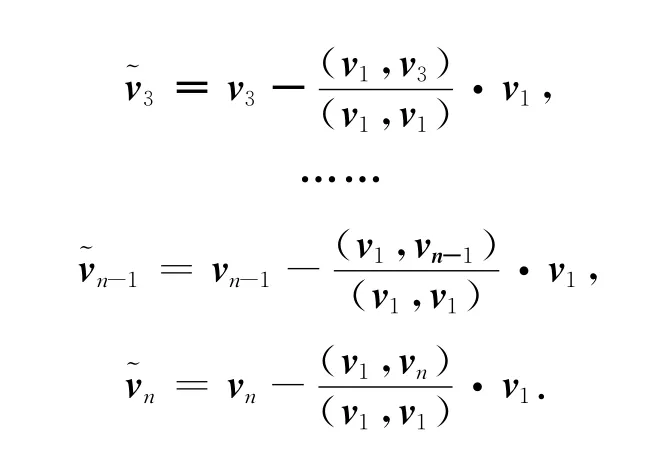
用矩阵表示为

将矩阵分块,令p=(a1,1,a2,1,…,ai-1,1)T,q=(ai+1,1,ai+2,1,…,an,1)T,r=(ai,2,ai,3,…,ai,n)T,l=(l1,2,l1,3,…,l1,n)T,I表示(n-1)×(n-1)单位矩阵,则式(2)变成

经第1步变换后得到第1列,与后n-1 列分别正交,于是有

这里0表示n-1 维零向量,所以可得到

所以向量-ai,1lT+rT可由-plT+B和-qlT+C线性表示.又因为将A的后n-1列分别与第1列正交后的矩阵的秩仍然为n,去掉第1列后剩余的矩阵的秩为n-1.所以剩余矩阵的行秩也为n-1.由式(3)知第i行可由其余行线性表示,则去掉第i行后剩余的n-1行线性无关,所以剩余的n-1 阶矩阵非奇异.
2 正交降阶分解算法
2.1 算法的构造
为求解线性方程组(1),记A的第1列中第1个不为零的元素为ai,1,先将矩阵A的第1列v1与后n-1列v2,…,vn分别正交,这等价于将矩阵A右乘矩阵P,于是线性方程组变成下列的等价形式:

对矩阵A=[v1,v2,…,vn-1,vn]∈Rn×n,现在将后n-1列v2,…,vn分别和第1列v1正交化,将Gram-Schmidt正交化后A的各列记为则原方程变为


将矩阵A第1次正交化后的n阶矩阵去掉第1列和第i行,剩下的n-1阶非奇异方阵记作A2.由定理1知,线性方程组(2)的系数矩阵中第i行与其它行线性相关,去掉第i行的n-1阶非奇异方阵即为A2.将b-v1y1去掉第i个元素后的向量记作,于是n阶线性方程组(1)转化为n-1阶线性方程组,以上过程称为正交降阶的过程.对得到的新的低阶线性方程组重复以上步骤,直到降为一阶线性方程.在重复正交降阶的过程中分别设yk=xk+lk,k+1xk+1+…+lk,nxn,k=1,…,n.最终可求解得到y=(y1,y2,…,yn)T.因而有

最终将一个n阶线性方程组转化为一个n阶上三角线性方程组,利用回代法可求得其解.
算法1 正交降阶分解算法
第1步:令k=1,=x.
第2步:记A的第1列中第1个不为零的元素为ai1,将矩阵A的第1列与其它列分别正交(也就是对A作列变换),正交后的各列记作v1,v2,…,vn-k+1,得到即v1y(k)+v2xk+1+…+vn-k+1xn=b,其中y(k)是xk,xk+1,…,xn的线性组合,且各项系数构成R的第k行元素.
第3步:利用各列与第1 列的正交性,求得y(k),得到v2xk+1+…+vn-k+1xn=b-v1y(k),去掉其系数矩阵的第i行,去掉右端b-v1y(k)的第i个元素,得到新的n-k阶方程.系数矩阵、未知向量和右端项仍记作和b.k=k+1,若k<n返回第2步,若k=n则进入第4步.
第4步:得到等价上三角线性方程组Rx=y,求解上三角线性方程组.
2.2 算法的复杂性分析
下面考虑正交降阶分解算法的运算量.运用正交降阶法,运算量为个flops;而利用Gram-Schmidt正交化,将n阶系数矩阵QR 分解需要个flops.
由表1可知,从运算量来看,高斯消去法是解线性方程组最经济的方法.尽管如此,有下面理由说明为什么仍然要考虑正交化方法.
对于病态问题,正交化方法更加可靠,也就是说正交化方法能更好地保持数值稳定性,不必像高斯消去法那样担心“增长因子”.

表1 各种直接法运算量比较Tab.1 Computational comparison of various direct methods
3 数值实验
例1 首先在MATLAB 上随机生成n阶非奇异的矩阵,然后将运用Gram-Schmidt正交化进行QR 分解,将所占用的CPU 的时间与正交降阶分解算法所占用的CPU 的时间进行对比,结果如表2 所示.

表2 Gram-Schmidt QR 分解法与算法1CPU 占用时间对比Tab.2 Comparison of CPU time between Gram-Schmidt QR decomposition method and algorithm 1 (s)
从CPU 的占用时间来看,当n=500,1 000,2 000,5 000时,Gram-Schmidt QR 算法大约是算法1所占用时间的1.23,2.31,2.82,3.61倍,且阶数越大,优势越明显.
例2 设矩阵

a=ones(1 000,1),A*a=b,Ax=b的精确解为x=ones(1 000,1).
LU 分解方法和算法1求解求线性方程组(1)的过程对比如图1 所示.
在图1中,C表示解的分量,S表示解.
例2 表明与运算量最少的高斯消去法相比,运算量次少的算法1具有较强的数值稳定性.
例3A取病态矩阵的典型Hilbert矩阵.A=hilb(8),x=ones(8,1),b=A*x,此方程的精确解为x=ones(8,1).用不同方法求解该方程组,得到的结果如表3 所示.
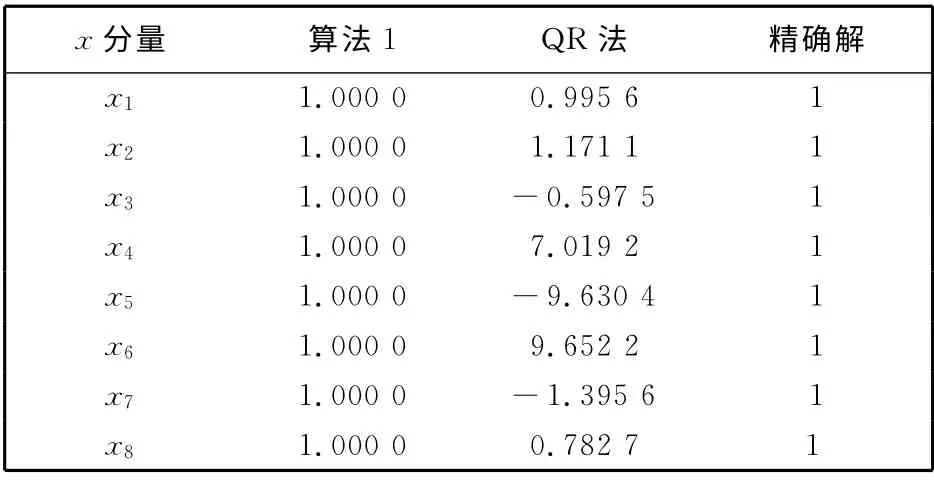
表3 算法1与QR 方法的求解数值结果Tab.3 Comparison result for algorithm 1and QR decomposition method
例3 表明对病态Hilbert 矩阵,算法1 较Gram-Schmidt正交化QR 方法数值更稳定.
从上述数值实验的结果可以看出,本文提出的正交降阶法不仅运算速度得到了很好的改善,运算精度也得到了提高,而且具有良好的数值稳定性.

图1 算法1和LU 分解法的对比Fig.1 Comparison between LU decomposition method and algorithm 1
[1]Golub G H,Van Loan C F.Matrix Computations[M].Baltimore:The Johns Hopkins University Press,1996.
[2]徐树方.数值线性代数[M].北京:北京大学出版社,2011.
[3]徐树方.矩阵计算的理论与方法[M].北京:北京大学出版社,1995.
[4]Strang G.Linear Algebra and Its Applications[M].2nd ed.New York:Academic Press,1980.
[5]Ruhe A.Numerical aspects of gram-schmidt orthogonal-ization of vectors[J].Linear Algebra and its Applica-tions,1983,52-53:591-601.
[6]Giraud L,Langou J.Rounding error analysis of the classical gram-schmidt orthogonalization process[J].Numer.Math.,2005,101(1):87-100.
[7]Rice J R.Experiments on gram-schmidt orthogonalization[J].Math.Comput.,1966,20(94):325-328.
[8]Daniel J W,Gragg W B,Kaufman L,et al.Reorthogonalizationand stable algorithms for updating the gramschmidt QR factorization[J].Math.Comput.,1976,136(30):772-795.
[9]Giraud L,Langou J.When modified gram-schmidt generates a well-conditioned set of vectors[J].IMA Journal of Numerical Analysis,2002,22(4):521-528.
[10]Wang C L,Yan X H.On convergence of splitting iteration methods for non-Hermitian positive definite linear systems[J].International Journal of Computer Mathematics,2013,90(2):292-305.
[11]Meng G Y,Wang C L,Yan X H.Self-Adaptive Non-Stationary Parallel Multisplitting Two-Stage Iterative Methods for Linear Systems[M].Berlin Heidelberg:Springer-Verlag,2012:38-47.
