基于波碰撞算法的机器人路径规划研究

王宇燕，邓高寿，马 田，李 丽

（1.中国北方车辆研究所 网络与信息中心，北京 100072；2.中国北方车辆研究所 总体部，北京 100072；3.中国北方车辆研究所 传动部，北京 100072）

0 引言

机器人在空间自由活动时，要解决的首要问题是路径获取问题.这通常依赖于机器人和目标点的位置信息，希望有一种可靠且有效的算法，求出一条最优轨迹将两点连接，同时满足各种不同类型的约束，如避开障碍物，最小转弯半径，最大加速度，最大能量消耗和时间消耗等.机器人路径规划需要考虑的因素主要有：环境的不确定性和动态特性，规划算法的实时性、有效性与最优性，以及满足机器人本体运动约束的能力［1-5］.移动机器人的研究越来越注重于在崎岖地形和存在大量障碍物的复杂环境中自主导航［6］，根据自身传感器对环境的感知，自行规划出一条安全的运行路线［7］.栅格分解法是目前广泛研究的路径规划方法之一，它把移动机器人的运动环境分解为多个简单的栅格，并根据它们是否被障碍物占据来进行状态描述.障碍物栅格和非障碍物栅格具有不同的标识值，它能够快速直观地融合传感器信息［8-14］.本文研究的机器人作业环境为二维平面大小一定的矩形地形，机器人行走时仅限于作原地转向或直线行走.在离散区域上用栅格法，选择任意位置为起始点和目标点，两个搜索波的速度相同，向各方向传播，既搜索路径又经历波传播过程，遍历障碍物，两个波前沿的初始交点为两点间最短路径.路径规划算法经过计算机模拟，证实可行有效.下面将以最佳的、最容易形成的菱形波+方波和菱形波+菱形波＊+方波为对象重点研究.

1 路径规划的基本原理

采用波碰撞法的基本思想确定未知路径，即在地图上的起始点S和目标点F同时发出搜索波［4］（如图1 所示），两个搜索波的速度相同，向各方向传播，遍历障碍物.两个波前沿的初始交点为两点间最短路径，因此只要找到其中一个起始点与另外一个已知点（或者与已经找到的点）重复进行上述过程，就可以在同一最短路径上确定所要搜索的另外一点.以此类推，可以找到整个路径或其中某一段路径所需要的点数.计算机模拟波传播过程时，主要应用逻辑运算.

图1 波碰撞物理图像Fig.1 Physical picture of wave collision

为确定最佳的、最容易形成的波，研究了4种简单类型的波，如图2 所示.

图2 4种简单类型的波形Fig.2 Four kinds of simple waves

经研究大量实例后，得出以下结论：图2（c）的波和图2（d）的波传播时碰撞数量最少，算法生成的图2（c）所示的波最简单，故视它为基础波.

2 规划路径算法的研究

2.1 离散波前沿和参考圆间的差

研究菱形波+方波交替形成的离散波前沿的特性.在研究前，需先证明几个命题.

命题1 设菱形波数用np表示，方波数用nf表示.离散波前沿是由所有相邻单元的中心所连成的八角形（参见图3），其参数有如下关系：

式中：δ为单元的尺寸.

图3 离散波前沿相邻单元中心连成的八角形Fig.3 The octagonal connected by discrete wave front adjacent units centre

菱形波+方波的总波数为n＝np+nf，用归纳法来证明命题1.当n＝1时，显然命题1成立.假设当n＝k时命题正确，则需要证明n＝k+1时该命题也正确.

证明 共有两种情况存在.第一种情况：假设第k+1 步长时波的前沿形成菱形波.此时，波前沿只在正交的方向上形成，八角形的垂直边和水平边平行移动，其长度M不变，按照归纳法长度（括号中上角标k表示步长序号）.第k步长对角方向是方形，形成“小梯”.k+1 步长形成小梯，它由个方形和沿着每端与它相连的一个方形形成，因而在第（k+1）步长小梯由个方形组成，其长度为因此对菱形波前沿而言，命题成立.

第二种情况：假设k+1步长时波的前沿呈方波.那么，每个垂直方向和水平方向构成的八角形与向它增加的方形一同平行移动，增加方形是从两侧沿着一方形.因此，第k+1步长的参数M将增加2δ，即对角线“小梯”形成的方形数量此时仍然不变，因此对角线长度d（k）不改变，命题完全成立.

从波的传播点到波的前沿的最大距离可自然地确定T1和T2分别为第一种和第二种情况相应的最大距离（参见图4），因而离散波前沿和基准波间的差θ为）

式中：R＝nδ为该时刻基准波的半径.不难证明

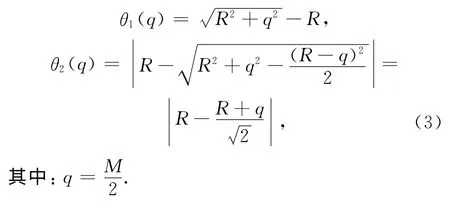
图4 第一种和第二种情况相应的最大距离T1和T2Fig.4 The biggest distance T1and T2

图5 所示的是θ1（q）和θ2（q）的函数曲线.粗线表示函数曲线θ（q）.函数θ（q）在函数θ1（q）和θ2（q）交点q＊处达到最小值，则有

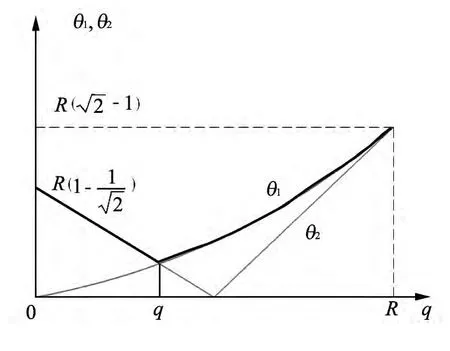
图5 函数曲线θ1（q）和θ2（q）Fig.5 Function curves ofθ1（q）andθ2（q）

求解方程（4），得到其正数根为

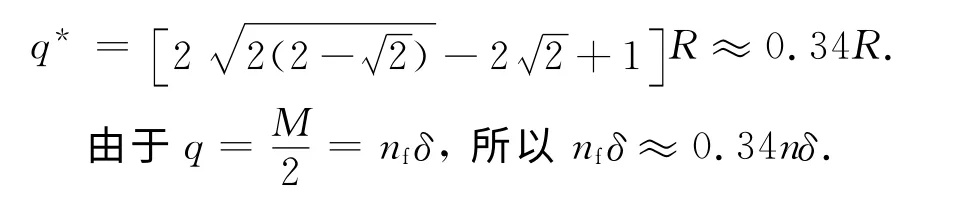
由此可得θ（q）的最小值，因而对于离散波，为了使离散波和基准波的差异达到最小，其中使用的“方波”数量大约是菱形波的一半.例如，“菱形波+菱形波＊+方波”恰与n≤93时每个第三步长处最佳波相重合.

将q＊值代入到θ1和θ2中计算θ的最小差异值（代入哪个代数式不重要，因为θ1（q＊）＝θ2（q＊），则有

引入不同离散波的距离θ值，对“方波”（q＝R）

对于菱形波，q＝0，则有

对菱形波+菱形波＊+方波，q＝nfδ＝则有

应当指出的是：第一，若上述差值θ（q）中增加常数项当前沿不是连接各个单元中心的直线，而是这些单元的本身时，则Δ（q）＝θ（q）+将能确定圆周和离散前沿任何点间的差.第二，可知最小估计值（q＊，θ＊）在离散波形成的最终时刻是正确的，且在离散波形成期间，q值是变化的.例如，菱形波+菱形波＊+方波周期为三步，其q值的变化范围为

2.2 碰撞点数

在地形连续地图（区别离散地图）上，两个连续波的碰撞点数是无限的.如图6 所示，其中阴影部分表示障碍区域，图中所标为连接起点S和目标点F相同长度路径.明显地，障碍布置可无限多.由点S和点F传播出的波碰撞线是路径中点的集合，路径多，碰撞点数也无穷多.

图6 起点S和目标点F两个连续波碰撞点数Fig.6 Two continuous waves collision points betweet starting point Sand target point F

在离散地图和离散波上，碰撞点数p总是有限的.事实上，设地图是一边长为L＝nδ的方形，行驶一段距离L／2 后，波沿p个不同方向传播，完成N／2 步长.根据命题1，在N／2 距离波前沿处，单元数最多为G＝4N-2，是方波.波传播方向的数量最多的是前沿每第二单元为障碍的情形.因而，N／2 步长处波传播方向的数量（也就是说碰撞点数）p不能大于G／2，则有

2.3 研发算法的特点

图7 表明设计的算法并不总是能够选出最佳路径.两波菱形波+菱形波＊+方波分别沿传播起始点S和目标点F传播.设图中阴影部分表示障碍，L1和L2是起始点S到目标点F传播的两种可能路径，则由于选L2而在路径第10步被撞；若选路径L1，则两波在路径上第11 步碰撞.因此，根据设计算法，选择路径为L2.在同一时间直接计算出路径L1和L2，则路径L1长度短于路径L2，因此算法生成的路径不是最优路径.需要注意的是，按照离散波碰撞法规划路径时，与最优路径的最大偏差为2θ（n）.

图7 设计算法选择的路径Fig.7 Path selection with design algorithm

下面几例都说明，就快速动作方面，单向路径算法和双向路径算法截然不同.基于单一波扩散法的无障碍地形图，从点S到点F选择路径时，占据面积πR2（R-S和F之间距离）；而基于碰撞波法，占据面积为πR2／2，即小1／2，因而运行时间也缩短约1／2.然而，在图8 中，利用双向路径算法解决规划路径问题比用单向路径算法的时间长.事实上，基于点S单一波传播法的路径规划法，占用10个栅格可以找到S点到F点的路径；而基于“菱形波+菱形波＊+方波”碰撞波的路径规划法，要找到S点到F点的路径，除了占用10个栅格以外，还要用45个栅格.

图8 双向路径算法和单向路径算法用时比较Fig.8 Comparison between the time of bidirectional path algorithm and one-way path algorithm

在路径规划法中，与机器人工作时间相比，存储特性更为重要，因为行走路径所用的时间很大程度上由移动机器人的速啡决定.

下面证明设计算法的一个重要属性：矩形障碍碰撞波只出现在图9中3个单元的1，2，3中之一.首先，证明如下的定理.

定理1 参考点（方形栅格中心）彼此可见x-y.U0为离散地图单元集，段［X，Y］通过这些单元，至少有一个点（单元）U0（设所有点U0不包括障碍）对应参考点U（x）和U（y）传播出来的离散波碰撞点.

证明 首先考虑区域无障碍的情况.设碰撞在U（z）∉U0单元中，则单元为U（z′），其中z′相对线段中心［x，y］的对称点z，同样包含碰撞点集.由于碰撞点集是由一个以上的点组成，因此意味着碰撞沿参考八角形的一边，然后线段［z，z′］通过所有单元，其中包含U0单元，也是碰撞点.这样，在无障碍地形情况下成立.由于可视区波形与作业环境障碍无关，U0依照条件于可视区，定理在有障碍情况下成立，因此用此定理证明下面的命题.

命题2 当地形有矩形障碍时，该算法的迭代只在其中1，2，3三个单元之一结束（图9）.

图9 有矩形障碍时算法迭代的结束Fig.9 The end of the algorithm＇s iteration at rectangular obstacle

证明 设碰撞波发生在阴影区边界突变的附近Ω，从S到极点PS观察，相对应于PS单元外侧.设碰撞之前F传出扩散波时产生下一个波源PF（波到达可视区边界产生源），然后PS和PF相互可见，因此根据定理碰撞一点位于区域Ω内.这意味着还会有一个迭代（根据碰撞点选择规则）.不难看出，只有当碰撞点与上述一种情况下相一致时，才可以结束.

2.4 连续波和离散波之间差在任意位置下的广义含义

在连续地图A上，当有障碍时，由于在一般情况下估算点a1到a2点行走耗能没有意义，因此点S（a1）与点S（a2）间的距离含义失去了其本身的含义.此时，引入函数a（a1，a2），该函数由地图A上任意两点a1，a2∈A决定，等于点a1到点a2允许路径最小的可能长度（允许路径是指不与障碍物相的交路径）.该函数是A的度量，不是ρ的度量.

设搜索波波源为点a∈A，以单位速度传播，τa（x）为波经过点x传播的时刻，则由定义可知α（a，x）＝τa（x）.自点a∈A传出波前沿在时刻t用代号γ′（a）表示，为封闭曲线（曲线部分与障碍边界重合），是时刻t波的边界.设nu（z）为自单元u∈U（U为地形离散图）传播出的离散波前沿用时，通过单元z.函数β（u，z）＝nu（z）用于模拟离散地图U上的距离α（在地图上规定相应度量）.自u∈U点传播前沿，用时刻u离散波表示Fn（u）.

引入映射，称其为从地图到地图的投影：

u→A（u）为单元u∈U对应连续地图A上的区域（此时是正方形）.u→a（u）为单元u∈U对应连续地图上的一个参考点a（U）∈A（u）.设这一点在正方形A（u）的中心.a→u（a）为点a∈A对应a∈A（u（a））条件下的离散图单元.

设正方形A（u）的边长等于δ.考虑两个同时以速度为δ传播的搜索波（以下称离散波和连续波），由单元u0源传播出的波称为离散波，由点a0＝a（u0）源传播出来的波称为连续波，引入下列代号：

φn（u0）＝A（Fn（u0））为离散波前沿在连续波上的投影；为相应的连续波前沿在离散地图上的投影；为以速度为δ传播，经过x点相应的连续波通过的时刻.

它有以下含义：如果对在步长n（x∈φn（u0））的离散波前沿向连续图上投影点x，用δn值作为距离a（x，a0）α0＝a（u0）估值（如果y∈γn（a0）），它是精确值α（y，a0），这一估计误差不超过Δn（n）.

对连续波前沿向离散地图投影进行同样的推导，得到值

它有一个类似的含义，但适合离散图.因此，Δn（n）确定连续波和离散波在连续地图（度量α）上投影间的最大差，Δu（n）值确定离散波和连续波在离散地图（度量β）上投影间的最大差.

设A（u）区域要么完全包括障碍，要么完全没有障碍.那么，这意味着

考虑连续地图上参考点的有限集合

同样引入下列一些代号：

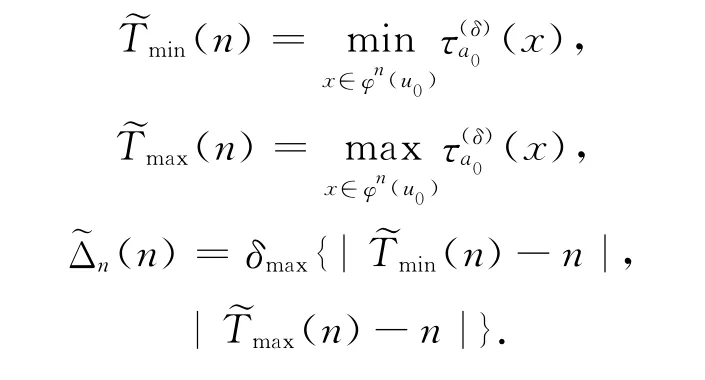
命题3 有下列不等式

证明 显然Tmin（n）＜～Tmin（n）.从另一方面

现在估计一般情况下的波差值.连续搜索波和搜索波Φn（U0）的传播如图10 所示.在开始时刻有个波源a（u0）＝x，设Vx为由点x见到的点集.则

a）对区域Vx内的波，差根据公式（1）计算；

b）从源a（u0）传播波到达边界∂V（a（u0））产生源.连续波是在其中一个栅格顶点，参考波Φn（U0）是在栅格参考点（参见图10）.

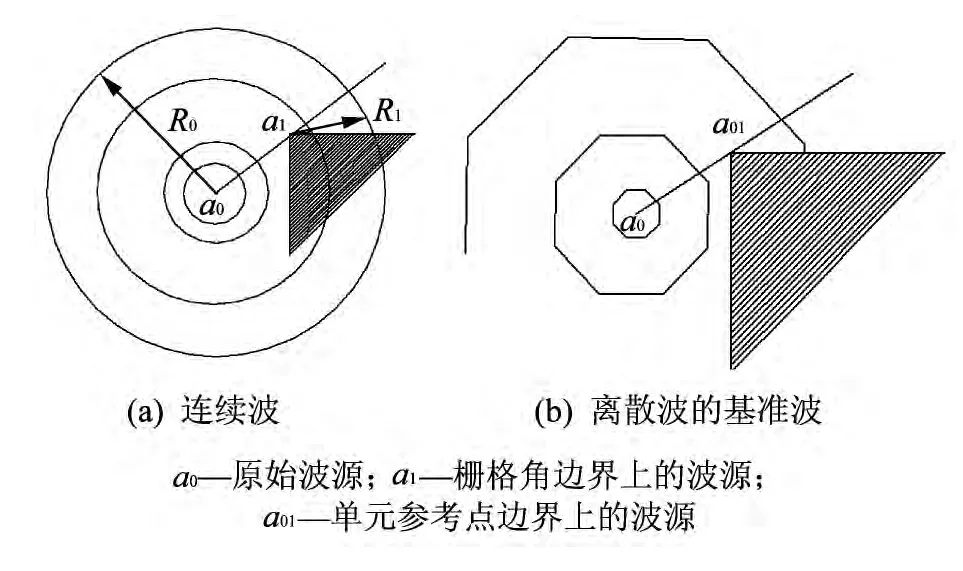
图10 连续搜索波和搜索波Φn（U0）Fig.10 Continuous search wave and search waveΦn（U0）

因此，连续地图上波前沿在任何时刻都受有限源的影响，在可见区域边界上彼此“点燃”.研究参考波源a0，a01，…，a0k在时刻n的集合，用代号L表示彼此“点燃”源的最大链，得到ΔA（n）的估计值.

式中：li为从a0i-1到a0i的步长数，向目标点源最大可能链进行合成.

不等式中第一加数项由向链运动抵达目标时点源互相“点燃完”的a0，a01，…，a0k链确定.第二加数项由于连续源和参考波不匹配造成误差.

3 结论

1）“菱形波+菱形波＊+方波”离散搜索波在步长n≤93时，每个第三步长与所研究波的级别的最佳波相重合.

2）对于这一类问题，用本文算法描述地形时，与传统可视图类型描述相比，内存增益.

3）根据算法规划的路径通过了附近障碍的极点.

4）给出了任意地形离散波和连续波间差的广义概念.

［1］陈洋，赵新刚，韩建达.移动机器人3维路径规划方法综述［J］.机器人，2010，7（5）：568-576.Chen Yang，Zhao Xingang，Han Jianda.Review of 3D path planning methods for mobile robot［J］.Robot，2010，7（5）：568-576.（in Chinese）

［2］顾幸方.移动机器人未知环境避障研究［J］.传感器与微系统.2011，30（5）：16-20.Gu Xingfang.Obstacle avoidance study for mobile robot in unknown environment［J］.Transducer and Microsystem Technologies，2011，30（5）：16-20.（in Chinese）

［3］于红斌，李孝安.基于栅格法的机器人快速路径规划［J］.微电子学与计算机，2005，22（6）：98-100.Yu Hongbin，Li Xiaoan.Fast path planning based on grid model of robot［J］.Microelectronics ＆Computer，2005，22（6）：98-100.（in Chinese）

［4］丁伟，李海波.一种移动机器人避障与追踪技术研究［J］.制造业自动化，2012，18：11-44.Dingwei，Li Haibo.A mobile robot obstacle avoidance and tracking technology research［J］.Manufacturing Automation，2012，18：11-44.（in Chinese）

［5］张海英.移动机器人路径规划研究现状及展望［J］.微型机与应用，2011，30（2）：5-8.Zhang Haiying.Research progress and future development of mobile robot path planning［J］.Microcomputer＆Its Applications，2011，30（2）：5-8.（in Chinese）

［6］朱大奇，颜明重.移动机器人路径规划技术综述［J］.控制与决策，2010，25（7）：961-967.Zhu Daqi，Yan Mingzhong.Survey on technology of mobile robot path planning［J］.Control and Decisition.Jul.，2010，25（7）：961-967.（in Chinese）

［7］夏梁盛，严卫生.基于栅格法的移动机器人运动规划研究［J］.计算机仿真，2012，29（12）：229-233.Xia Liangsheng，Yan Weisheng.Study on mobile motion planning based on grid method［J］.Computer Simulation，2012，29（12）：229-233.（in Chinese）

［8］孙茂相.基于规则的移动机器人实时运动规划［J］.控制与决策，1997，7（4）：322-326.Sun Maoxiang.Rule-based real-time motion planning for mobile robots［J］.Controlanddecision，1997，7（4）：322-326.（in Chinese）

［9］张玉婷.自主移动机器人避障算法研究及展望［J］.黑龙江科学，2013，7（4）：59-62.Zhang Yuting.The research and prospects of obstacle avoidance algorithm for autonomous mobile robot［J］.Heilongjiang Science，2013，7（4）：59-62.（in Chinese）

［10］苏丽颖.基于障碍物影响系数的机器人路径规划方法［J］.北京工业大学学报，2008，34（5）：459-465.Su Liying.A robot path-planning method based on the obstacle influence factor［J］.Journal of Beijing University of Technology，2008，34（5）：459-465.（in Chinese）

［11］许斯军，曹奇英.基于可视图的移动机器人路径规划［J］.计算机应用与软件，2011，3（1）：220-236.Xu Sijun，Cao Qiying.A visibility graph based path planning algorithm［J］.Computer Applications and Software，2011，3（1）：220-236.（in Chinese）

［12］张学习，杨宜民.基于全向视觉的移动机器人实时全局地图构建［J］.计算机测量与控制，2011，19（3）：643-646.Zhang Xuexi，Yang Yimin.Global map building based on omni-vision for mobile robot［J］.Computer Measurement ＆Control，2011，19（3）：643-646.（in Chinese）

［13］郑秀敏，顾大鹏.基于栅格法-模拟退火法的机器人路径规划［J］.微计算机信息，2007，23：247-249.Zheng Xiumin，Gu Dapeng.Robot path planning based on grid method with simulated annealing［J］.Microcomputer Information，2007，23：247-249.（in Chinese）

［14］杨建勋.一种改进的蚁群算法在机器人路径规划应用［J］.科技通报，2012，28（12）：208-211.Yang Jianxun.An improved ant colony algorithm for path planning of robot［J］.Bulletin of Science and Technology，2012，28（12）：208-211.（in Chinese）