光纤环圈数控缠绕机主轴结构优化设计

张 鹏，张学良，杨瑞峰

（1.兰州理工大学 机电工程学院，甘肃 兰州 730050；2.中北大学 电子测试技术国防科技重点实验室，山西 太原 030051；3.太原科技大学 机械工程学院，山西 太原 030024）

0 引言

光纤环圈数控缠绕机主轴部件是光纤环圈实现旋转运动的执行件，是光纤环圈缠绕机中的重要零部件.它的性能直接影响着整个光纤环圈缠绕机的使用性能，旋转精度不高会导致光纤上局部应力分布不均匀，出现匝间间隙过大、回叠、塌陷等现象，直接影响光纤环圈的缠绕质量，对光纤环圈产品的整体性能影响很大［1］.

光纤环圈数控缠绕机主轴的结构参数是决定主轴系统性能的最重要的指标，因此针对主轴的结构参数进行优化设计非常重要［2］.关于机床主轴结构的优化设计国内外学者已经提出了不少方法，主要分为两类：一类为ANSYS软件提供的零阶和一阶优化方法.零阶优化是通用的函数逼近优化方法，这种方法不易陷入局部极值点，但优化精度一般不高；一阶优化是基于梯度寻优的一阶优化方法，这种方法精度较高，但极易陷入局部最小值.二者都存在一定的缺陷，对于简单的、精度要求不高的模型，采用ANSYS有限元优化的方法可以快速准确地实现主轴结构的优化设计［3-7］.另一类采用优化能力较强的进化算法为工具，对主轴结构进行优化设计［8-10］.传统的优化设计方法存在着求解过程复杂和寻优过程容易陷入局部最优解的问题，而果蝇算法的优点是擅长全局搜索且对优化问题的函数特性无特殊要求，是一种优点较多的优化算法.

本文在充分考虑主轴传动件位置、作用力及轴承刚度的基础上，通过对所建立主轴结构的力学模型的分析，获得该模型的数学表达，以主轴结构尺寸及主轴径向跳动（安装光纤环圈骨架处）不超过5μm 为约束条件，以主轴质量最轻为目标，建立其优化设计的数学模型，进而采用果蝇算法优化搜索机制，在可行域中搜索并确定最优的设计方案，从而获得对光纤环圈数控缠绕机主轴传动位置、轴径等的最佳组合优化方案，实现主轴结构的优化设计.

1 主轴优化数学模型

光纤环圈数控缠绕机主轴由左右两个半主轴通过刚性动力锁链接构成.左、右半主轴各为一空心的阶梯轴，采用两支承结构.左、右半主轴外侧端的轴承由一个推力球轴承和一个角接触球轴承组成，用于承受轴向力和径向力.在左、右半主轴靠近外端侧各装有一传动齿轮，用于传递动力，带动主轴旋转运动.光纤环圈数控缠绕机主轴结构如图1 所示.

图1 光纤环圈数控缠绕机主轴结构图Fig.1 Structure diagram of the spindle of fiber optic ring NC winding machine

1.1 确定设计变量

主轴材料一旦选定，其重量只由主轴的内径D0，外径D1，D2，D3及主轴各段长度L1至L7决定，然而D3，L3，L4，L5为定值，不能作为设计变量，因此以主轴的内径D0，外径D1和D2，短主轴的长度L2，长主轴的长度L6作为设计变量.主轴优化设计变量可表示为：

数控缠绕机主轴剖面图如图2 所示.

图2 数控缠绕机主轴剖面图Fig.2 The sectional view of the spindle of fiber optic ring NC winding machine

1.2 建立目标函数

根据设计要求，以光纤环圈缠绕机主轴体积最小为追求的目标，因此优化目标函数为

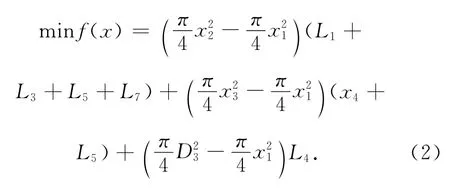
1.3 约束条件

在设计主轴时，由于光纤环圈质量较轻，主轴转速较慢，且安装在主轴上与主轴同心，负载转矩较小.转角、扭转变形和强度等约束条件对主轴挠度的影响相对于主轴自重的影响很小，可以忽略不计［11］.因此，该主轴优化模型约束条件主要包括：

1）挠度约束.由主轴上安装光纤环圈骨架处的挠度不得超过5μm，建立刚度约束g1（x）＝y-5×10-6≤0.

2）设计变量的边界约束.由主轴各几何尺寸，建立主轴各尺寸的边界约束.

由此得到约束方程，如式（3）所示.

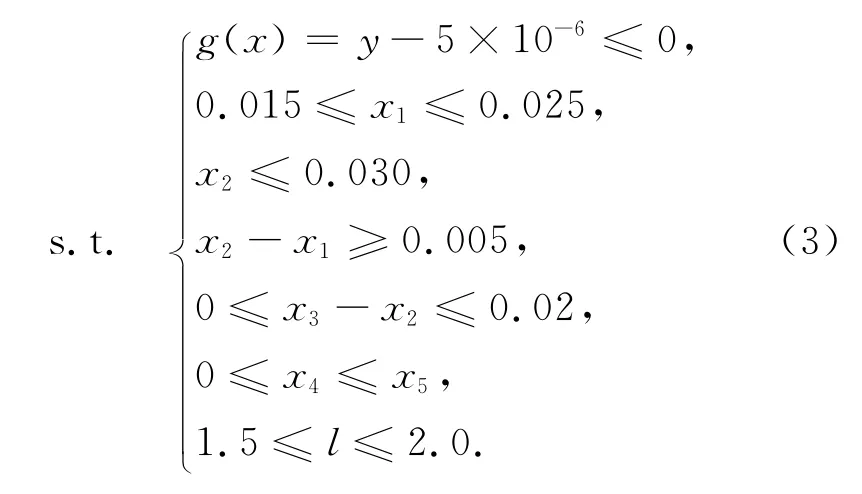
2 基于果蝇算法的光纤环圈缠绕机主轴优化设计

果蝇优化算法（Fruit Fly Optimization Algorithm，FOA）是从果蝇寻找食物的方法得到启发而提出的一种新型优化算法.果蝇在随机飞行方向的过程中，利用灵敏的嗅觉判断食物气味浓度，确定与食物的大致距离和飞行方向，然后再利用视觉向食物方向靠近.将果蝇觅食原理应用于优化算法，利用目标函数与目标值之间的差来寻找飞行方向，最终找到最优解［12］.由于果蝇种群是在全局范围随机飞行，因此可以避免局部最优，而且是多果蝇同时寻找，因此收敛速度快［13］.

依据果蝇搜索食物的特性，将果蝇优化算法归纳为如下几个主要步骤：

1）参数初始化.确定果蝇种群规模SizePop，最大迭代次数MaxIter和迭代终止条件δ，随机初始化果蝇个体位置.

2）随机初始化果蝇种群.

式 中：j∈ ｛1，2，…，SizePop｝，i∈ ｛1，2，…，MaxIter｝，a1，b1，a2，b2分别是随机数的取值范围，其数值根据具体情况而定.

3）由于无法确定优质食物源的具体位置，因此预先估计与原点的距离Dij，再计算味道浓度判定值Sij，此值为Dij的倒数.

4）将味道浓度判定值代入味道浓度判定函数（适应度函数）中，用来求出果蝇个体的味道浓度.

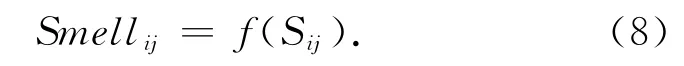
5）找出种群中味道浓度最佳的果蝇个体.

6）记录并保留最佳味道浓度值及其对应的x，y坐标，并将其与上一次迭代的最优结果进行比较，选择最优结果按照式（7）进行数据传递，此时种群中的其它果蝇个体利用视觉飞向该个体所在位置.

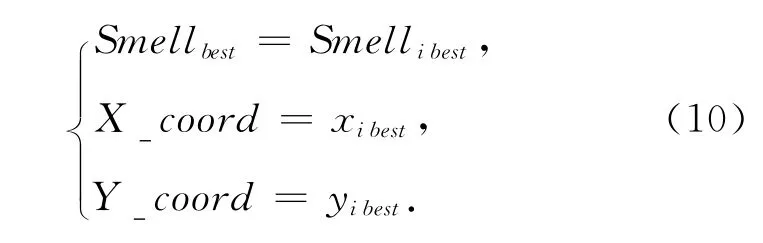
7）进入寻优迭代，重复执行步骤2）～6），直到程序满足迭代终止条件.

根据以上所述的果蝇算法的基本思想及光纤环圈缠绕机主轴结构优化设计的数学模型，以某光纤环圈缠绕机主轴为例，对其进行优化设计.初始参数的选择如下：材料选择为自重较轻的锌铝合金，其质量密度为ρ＝6 900kg／m3，L1＝0.1m，L2＝0.5m，L3＝0.1m，L4＝0.15m，L5＝0.05m，L6＝0.8m，L7＝0.2 m，D0＝0.06m，D1＝0.074m，D2＝0.076m.采用果蝇算法进行求解，取种群规模POPULATION＝200，最大迭代次数ITERATION＝600，程序独立运行20次，取20次运算所得平均结果.优化过程序列如表1 所示.

表1 优化过程序列表Tab.1 Sequence list of the optimized process

3 有限元分析验证

由于在进行优化设计建模时，对主轴的力学模型进行了一定的简化，并且忽略了主轴强度、扭转变形等约束条件的影响，所建立的优化模型是否准确还有待检验，因此对本设计所选用的光纤环圈数控缠绕机主轴结构进行了基于ANSYS的有限元分析，选用表1 中经果蝇算法优化后的尺寸及结果，验证经果蝇算法优化和经有限元分析后的结果是否一致.有限元分析结果如图3 所示，优化设计前主轴在工作状态下的最大变形为3.05μm，经优化后的最大挠度值为3.36μm，与表1 中优化后的数据基本保持一致，误差仅为1.57%.

图3 有限元分析结果Fig.3 Results of finite element analysis

4 结论

在充分考虑光纤环圈数控缠绕机主轴结构及其受力的基础上，对主轴结构的力学模型进行了简化，并以主轴结构质量（体积）最小为优化设计目标，以主轴结构最大挠度不超过5μm 等为约束条件，建立了其优化设计模型，并采用果蝇算法对主轴结构进行了优化设计.优化结果表明：在主轴最大挠度变化不大的情况下（与优化前相比，变化量约为8.01%），主轴质量（体积）得到了较大程度的减小（与优化前相比，减少了67.15%），有效地降低了主轴的质量.

［1］Lefevre H C.光纤陀螺仪［M］.张桂才，王巍，译.北京：国防工业出版社，2002.

［2］吴化勇.机床主轴部件有限元分析及优化设计［J］.机床与液压，2008，36（11）：850-851.Wu Huayong.FEM and optimization-design of spindle parts in machine tools［J］.Machine Tool ＆ Hydraulics，2008，36（11）：850-851.（in Chinese）

［3］吴佳燕，李郝林.基于Ansys的主轴系统有限元模型结构优化［J］.机械设计与研究，2010，26（6）：65-67.Wu Jiayan，Li Haolin.Spindle system finite element model optimization based on Ansys［J］.Machine Design and Research，2010，26（6）：65-67.（in Chinese）

［4］郑玲利，吕文阁.基于竞选算法的机床主轴结构优化设计［J］.机械设计与制造，2006（8）：35-37.Zheng Lingli，Lv Wenge.The optimization design of machine tools spindle structure based on competitive algorithm［J］.Machinery Design ＆ Manufacture，2006（8）：35-37.（in Chinese）

［5］杜官将，李东波.基于ANSYS的机床主轴结构优化设计［J］.组合机床与自动化加工技术，2011（12）：22-24.Du Guanjiang，Li Dongbo.Optimization design of the structure of machine tool spindle based on ANSYS［J］.Modular Machine Tool ＆ Automatic Manufacturing Technique，2011（12）：22-24.（in Chinese）

［6］徐燕.数控机床主轴结构的改进和优化设计［J］.机械研究与应用，2011（3）：115-117.Xu Yan.Improvement and optimization about spindle structure of CNC machine［J］.Mechanical Research ＆Application，2011（3）：115-117.（in Chinese）

［7］博嘉科技.有限元分析软件-ANSYS 融会与贯通［M］.北京：中国水利水电出版社，2002.

［8］Necmettin K.Machining fixture locating and clamping position optimization using genetic algorithms［J］.Computers in Industry，2006，57（2）：112-120.

［9］高海涛，许志沛，申士林.基于ANSYS Workbench的多层缠绕卷筒的结构优化设计［J］.机械设计与制造，2013（6）：15-17.Gao Haitao，Xu Zhipei，Shen Shilin.Optimization design of multilayer drum based on ANSYS workbench［J］Machinery Design ＆ Manufacture，2013（6）：15-17.（in Chinese）

［10］郭辰光，王鹏家，田鹏，等.基于遗传算法的数控机床主轴优化设计方法［J］.东北大学学报，2011，32（6）：850-853.Guo Chenguang，Wang Pengjia，Tian Peng，et al.Optimization design of CNC machine tool spindle based on genetic algorithm［J］.Journal of Northeastern University，2011，32（6）：850-853.（in Chinese）

［11］龚文明，喻道远，乐胜年，等.基于ANSYS的数控镗铣床主轴结构动态特性对比分析［J］.机械设计与制造，2012（12）：151-153.Gong Wenming，Yu Daoyuan，Le Shengnian，et al.The comparison analysis of dynamic characteristics of CNC boring and milling machine spindle structure based on ANSYS［J］.Machinery Design ＆ Manufacture，2012（12）：151-153.（in Chinese）

［12］Pan W T.A new fruit Fly Optimization Algorithm：Taking the financial distress model as an example［J］.Knowledge-Based Systems，2012，26：69-74.

［13］Pan W T.A new evolutionary computation approach：fruit fly optimization algorithm［C］.2011Conference of Digital Technology and innovation Management Taipei，2011.