基于遗传匹配追踪的图像修复算法

辛晚霞，杨 明

(中北大学理学院，山西太原030051)

近几年，图像修复是图像处理领域的研究热点，目前常用的算法有基于马尔科夫随机场的方法(FOE)［1］、基于整体变分的方法(TV)［2］、基于曲率扩散的模型(CDD)［3］和基于压缩感知(CS)的方法［4－6］等。基于 CS［7］的图像修复算法需要对图像进行稀疏表示，匹配追踪算法(MP)［8－9］是一种常用的稀疏表示方法，它以贪婪算法为核心，较其他稀疏算法更容易理解，并且逼近效果好，计算复杂度小。而MP在冗余字典库中的遍历式搜索使得计算量很大，需要巨大的存储空间。为了解决这个问题，人们提出了遗传匹配追踪算法(GMP)［10－14］，GMP 模拟生物进化现象寻找最佳原子。为了得到更理想的效果，文献［10－12］分别对编码方式、选择算子和搜索方式进行了改进。

本文结合GMP提出一种采用混合选择算子的图像修复算法，该算法在使用GMP对图像进行稀疏表示的过程中，使用精英保留策略、竞标赛选择方法和轮盘赌方法［15］相结合的选择算子，在变异过程中采用动态变异的方式，通过仿真实验验证算法的可行性。

1 基于GMP的图像修复算法

1.1 GMP 算法原理

Mallat和Zhang引入的MP是一个通过选取字典向量来优化逼近的贪婪算法。信号f的最佳逼近原子φp0∈D(D是过完备字典库)为

逼近残差为

通过从字典里选取另一最优原子φp1，进一步用MP逼近误差R，继续这一过程，得到l阶误差Rl(l=1，2，…，K)，最后得到信号的分解式

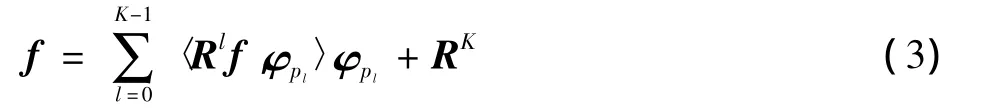
GMP将MP中的参数空间投影到编码空间进行编码，编码采用实数编码，设定初始种群规模Size、种群代数G、参数编码长度n，并形成初始种群pm，解码并计算种群中个体的适应值，得到本代最优个体，但不是全局最优的个体，判断m是否小于G，小于则进行遗传操作，在保留上一代优良基因的同时又加入了新的基因，大于G则跳出遗传算法，并带回最优个体的原子、残差及投影系数，判断原子个数是否小于K(稀疏度)，小于则继续进行迭代，否则停止，得到最终的原子及投影系数。

1.2 基于GMP的图像修复算法

图像修复是利用损坏图像的未被损坏信息，按照一定规则对损坏区域进行填补，利用压缩感知理论对损坏区域进行修复是一种新颖的方法。设图像的完整信息为f，未被损坏区域为yobs，则yobs=M f，M是掩模算子，损坏区域为y=f－yobs，图像具有稀疏性，所以f在字典D中可以稀疏表示

根据图像的全局稀疏性，未被损坏区域yobs和损坏区域y共用稀疏系数α，则图像修复问题可定义为

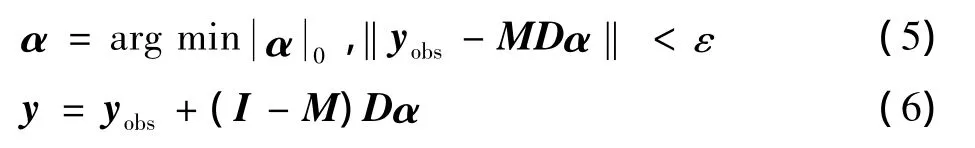
基于GMP的图像修复算法就是通过GMP求解式(5)得到系数α，然后利用式(6)恢复损坏区域y的过程。

2 改进的GMP图像修复算法

2.1 改进的选择算子

选择算子具有降低种群多样性和保护种群收敛性的双重作用，使用单一的选择算子会导致早熟并且降低种群的多样性。为了解决这个问题，在进化的前后阶段分别使用不同的选择算子来达到选择压力的改变，并且保留精英个体，将每代中最优的个体直接复制到下一代，而不经过交叉和变异操作，把最差的个体替换为最优的个体，在进化初期为了保护种群的多样性使用锦标赛选择方式来降低选择压力，而在后期为了加快收敛使用轮盘赌方法来提高选择压力。

2.2 基于改进的GMP图像修复算法

基于改进的GMP图像修复算法的具体实现步骤如下:

1)给定待修复图像的未被破损区域yobs和掩模算子M，选择合适的字典D，设置种群规模Size，种群代数G，参数编码长度n，稀疏度K，交叉率pc，变异率pm，迭代次数l=0，随机产生初始种群。

2)计算种群中每个个体的适应值eval(vi)，i=1，2，…，Size，即个体所对应字典D中的原子与残差R或yobs的内积，最高的适应值即为原子与残差内积的最大值。

3)选择运算:采用改进的选择算子对种群进行选择，即保留适应值最高的个体，直接复制到下一代，把适应值最低的个体替换为最高的个体，前G1代选择锦标赛方式进行选择操作，后G－G1代选择轮盘赌方式进行选择操作。锦标赛方式为随机两两一组进行竞赛，选择适应值最大的个体。轮盘赌方式为先计算选择概率pi及累计概率qi，即

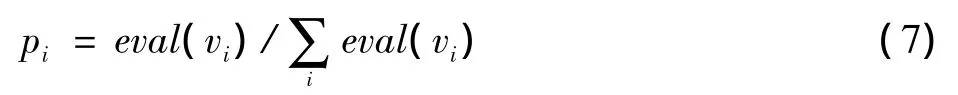
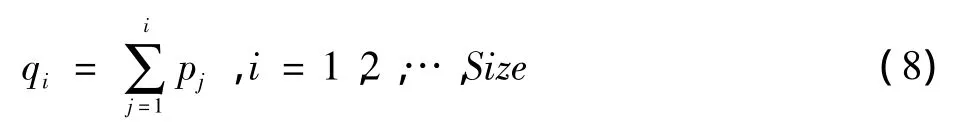
然后在［0，1］区间产生一个均匀分布的伪随机数r，若r＜q1，则选第一个个体v1;若qi－1＜r≤qi，则选第i个个体，依次进行下去。

4)交叉运算:采用算术交叉的方式，根据交叉率pc选出交叉个体，将交叉个体两两随机配对，根据以下方式产生后代。设双亲为v1和v2，交叉产生的后代为

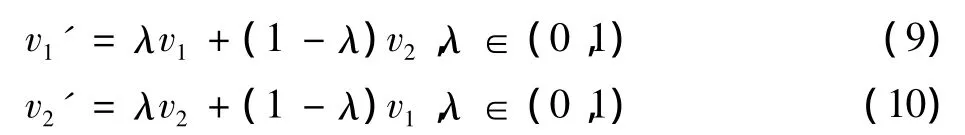
5)变异运算:根据变异率pm选出变异个体，设变异个体为v，则变异后的个体vm按如下方式产生

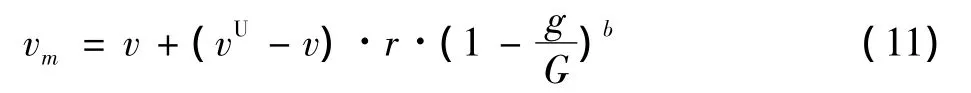
式中:vU为字典D变量的上界;r是［0，1］间的随机数;G是最大代数;g为代数;b为确定不均匀度的参数，取2。

6)判断种群是否收敛，若收敛转至步骤7)，否则，转至步骤3)。

7)通过解码得到最优个体对应的原子参数，并由参数计算出最优原子φpl，再将原子与残差作内积运算得到原子的系数αl。判断l是否小于K，是则转至步骤2)，否则转至步骤8)。

8)最后得到式(6)的稀疏系数 α ={αl，l=1，2，…，K}，对应的原子 D={φpl，l=1，2，…，K}，通过式(6)计算出损坏区域y。

3 实验结果及分析

3.1 图像修复的评价

本文对图像修复效果采用客观评价法进行评价，评价指标为信噪比，计算方法为

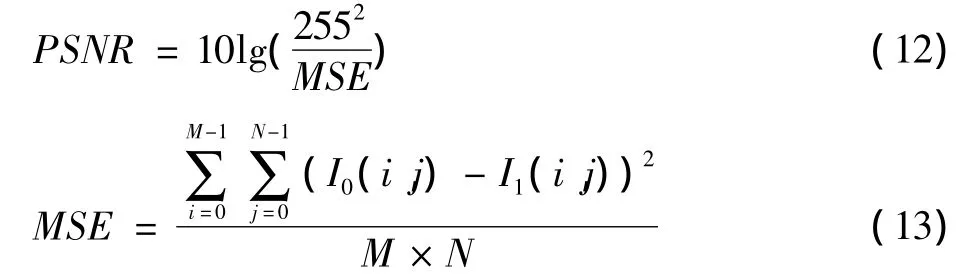
式中:I0，I1分别表示原图与修复后的图像，信噪比越高，修复的效果越好。

3.2 仿真结果

本节在小区域修复和文字去除等方面做实验验证算法的可行性，并与FOE方法、TV方法、CDD方法进行比较。表1给出了基于本文GMP图像修复算法的参数设置，字典D采用文献［16］中的2D几何字典。表2给出了3种算法修复3幅图像的信噪比。

表1 GMP参数设置

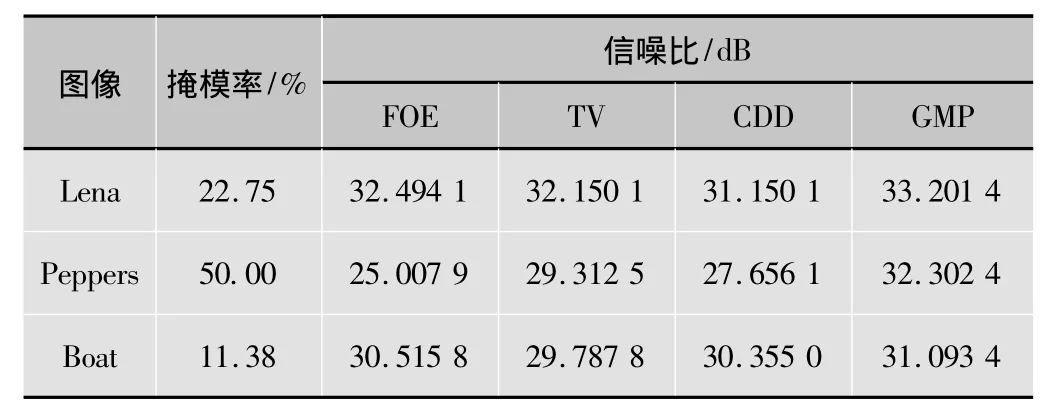
表2 实验结果

图1为对Lena图字母掩模后的修复，图1a为掩模后的图像，图1b为字母掩模，掩模率为22.75%，从图1c、图1d、图1e和图1f中可以看出:FOE方法在肩膀部位出现锯齿，帽子和图像左边界有阴影;TV方法在边缘部分的修复效果不是很理想;CDD方法有个别像素在修复时出现错误，边缘部分有些模糊;而本文方法无论在平滑还是边缘区域修复效果都很好，并且信噪比高。

图1 Lena修复

图2为对Peppers图随机掩模50%的修复，即有一半的信息丢失，从图2c、图2d、图2e和图2f中可以看出:FOE方法在某些边缘部分出现了锯齿;CDD方法对于边缘部分基本发生了模糊;TV和本文方法修复效果都很好，但是本文方法的信噪比更高一些。

图3为对Boat图用棋子格掩模后修复的图像，图3a和图3b中黑色区域为宽度2个像素的掩模区域，掩模率为11.38%，从图 2c、图 2d、图 2e和图 2f中可以看出:FOE，TV和CDD方法对船上的桅杆和船身修复时有阴影出现，而本文方法修复后的阴影很少，且信噪比高。

4 结论

本文提出一种基于GMP的图像修复算法，它将GMP与修复算法相结合，并改进了GMP的选择算子，采用精英保留策略、锦标赛选择方法及轮盘赌方法相结合的混合选择算子。该算法充分考虑了图像的全局稀疏信息，并使用适合细节描写的2D几何字典，采用GMP算法减少了计算复杂度。通过仿真结果可以看出:本文提出的算法有一定的应用价值，并且修复后的图像更接近真实图像。

图2 Peppers修复

图3 Boat修复

［1］陈佩.基于马尔科夫随机场图像恢复算法研究［D］.南京:南京师范大学，2008.

［2］ CHAN T，SHEN J.Mathematical models for local nontexture inpainting［J］.SIAN Journal on Applied Mathematics，2002，62(3):1019－1043.

［3］ CHAN T，SHEN J.Non－texture inpainting by curvature－driven diffusions(CDD)［J］.Journal of Visual Communcation and Image Representation，2001，12(4):436－449.

［4］ SHEN B，HUW，ZHANG Y，etal.Image inpainting via sparse representation［C］//Proc.ICASSP 2009 .［S.l.］:IEEE Press，2009:697－700.

［5］ FADILI M，STARCK J，MURTAGH F.Inpainting and zooming using sparse representation［J］.Comput.J.，2007，52(1):64－79.

［6］ GULERYUZLO.Nonlinear approximation based image recovery using adaptive sparse reconstructions and iterated de－noising－part II:adaptiveal gorithms［J］.IEEE Trans.Image Process，2006，15(3):555－571.

［7］宋允东.基于 JND的压缩感知图像编码［J］.电视技术，2012，36(14):15－18.

［8］ MALLAT S，ZHANG Z.Matching pursuit with time－frequency dictionaries［J］.IEEE Trans.Signal Processing，1993，41(12):3397－3415.

［9］ MCCLUREM，CARIN L，Matching pursuits with a wavebased dictionary［J］.IEEE Trans.Signal Process，1997，45(12):2912－2927.

［10］范虹，孟庆丰，张优云.用混合编码遗传算法实现匹配追踪算法［J］.西安交通大学学报，2005，39(3):295－299.

［11］李亚文，于凤芹.一种改进选择算子的遗传匹配追踪算法［J］.数据采集与处理，2011，26(2):177－180.

［12］高瑞.基于GA和过完备原子库划分的MP信号稀疏分解算法［J］.科学技术与工程，2008，8(4):914－918.

［13］高强.遗传算法降低匹配追踪算法计算量的研究［J］.振动、测试与诊断，2003，23(3):165－167.

［14］李亚文.遗传匹配追踪算法的研究与改进［D］.无锡:江南大学，2011.

［15］玄光男，程润伟.遗传算法与工程设计［M］.北京:科学出版社，2000.

［16］ OSCAR D，GIANLUCA M，ROSA M，et al.Geometric video approximation using weighted matching pursuit［J］.IEEE Trans.Signal Processing，2009，18(8):1703－1716.