基于DVB－T2的旋转星座解映射算法及其改进

石 康，王 萍

(中科院上海微系统与信息技术研究所，上海200050)

DVB－T2标准作为新一代欧洲数字视频广播标准，采用一系列广播和通信领域的最新技术和概念，包括旋转星座的应用。星座旋转也叫做信号空间分集(Signal Space Diversity，SSD)［1］，将符号按维度划分开来在空间层次上实现分集。扩大信号空间分集度主要在于对信号星座进行一定角度的旋转，使两个星座点之间的分集尽量达到最大。欧洲第二代地面数字广播标准DVB－T2采用了旋转星座作为可选模块来增强系统在频率选择性信道中的传输性能。DVB－T2系统中解映射器引入译码器的先验信息进行迭代解映射。文献［2］提出基于外在比特信息迭代的二维迭代LLR解映射算法，利用LDPC译码器的硬判决反馈降低迭代解映射器的运算复杂度，提高系统性能。不过仿真结果表明，调制阶数降低时，带来一定的误码率。

本文在传统的先验信息反馈算法的基础上，结合系统性能和运算复杂度进行设计，提出一些改进算法。

1 星座旋转技术

星座图旋转技术最早由K.Boulle和J.C.Belfiore提出，使系统达到更高的分集度，并且可以联合前向纠错来提升系统性能，从而增强系统对恶劣信道的抗干扰能力［3］。

DVB－T2标准中，提供了星座旋转作为比特交织编码调制(Bit Interleaved Coded Modulation，BICM)中的选用模块，该模块位于比特交织和单元交织之间［4］。例如图1，星座选择某种旋转表示把各星座点映射到I轴和Q轴的不同坐标，使分量变得相关。在时间和频率交织之前把经历过该模块的Q进行循环延迟，从而使实部和虚部信息割离。于是交织后发射出的星座点的I和Q值并不相关(不同的星座点的横坐标和纵坐标)。而在接收机中通过解交织环节后，把接收的I和Q值再结合，如此它们在衰落信道下历经独立的衰落。对于每个符号都需要同时获得I和Q信息才能确定。而在引入星座旋转后，即使在极恶劣的情况下，I和Q值中的某个全部遗失了，也不会完全地遗失信息，另一个值依旧含有所有的信息。因此只需要获得其中一个就能恢复这个符号。星座旋转技术带来了另外的分集，同一比特同步映射到的载波也相应增多，增加了分集阶数。

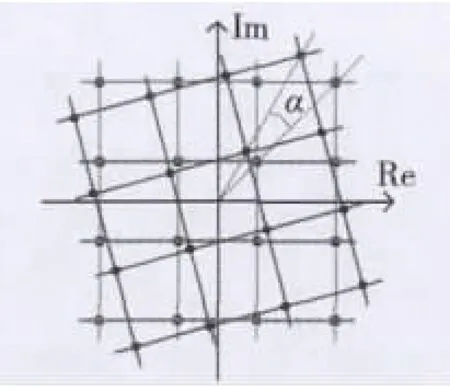
图1 16QAM星座旋转

在DVB－T2标准中，给出了不同调制方式下适当旋转角度参考值，见表1。不同星座映射选择的旋转角度与具体信道是不直接关联的，这里给出的，实际上是对全部可能应用于DVB－T2系统信道的一种折中［5］。

表1 DVB－T2标准中规定的星座旋转角度

2 基于硬判决的二维迭代LLR解映射

由于应用了旋转星座调制，解映射模块中必须应用二维LLR。LLR(对数似然比)是比特软信息的一种表示。对于第i位比特 (i=1，2，…，k)，有

式中:r为接收符号。假设bi=1时由2k－1个星座点发射的可能性是等概率的，则发射符号中bi=1时，接收符号r的条件概率为

式中:s为发射符号;为第i位比特取1的星座点的集合;σ2为噪声方差;rI和rQ分别是接收的I和Q值。

同理可以得到发射符号中bi=0时的情况，再假设发射符号bi取0和1的概率相同，得到LLR的表达式为

由于计算公式比较复杂且性能较差。文献［6］中引入了迭代结构，见图2。利用了LDPC译码器中其他位比特硬判决反馈给解映射器，进行迭代解映射。

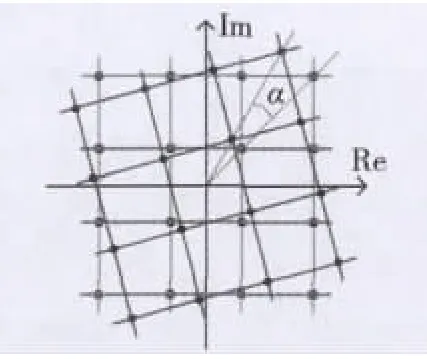
图2 二维迭代LLR解映射器

对除了第i比特以外的每个比特的软信息进行硬判决后再反馈给解映射器，这时接收符号在星座图上对应的只有两个可能发射星座点。LLR表达式由式(3)简化为

式中:SiI和SiQ表示发射符号第i位比特的I和Q值。与式(3)相比，运算复杂度明显降低，可以避免指数和对数运算。但在迭代结构中，首次解映射仍需使用软判决，输入到译码器中。

3 改进方法

3.1 k－2比特反馈

文献［2］中使用的硬判决反馈方法，虽然可以大大降低复杂度，但却带来了一定的错判率，系统性能需要通过迭代次数来弥补。本文提出的算法1的主要目的是在尽量少地增加计算量的情况下更有效地提升系统性能。手段是减少译码器硬判决反馈，扩大搜索星座范围。

以16QAM星座为例，原来的方法在次轮迭代解映射之后，发射范围被限制在一对星座点中，这时星座图降阶为一种特殊情况的BPSK。在硬判决二维迭代解映射算法基础上加以修改，将其余比特软信息都进行硬判决反馈改为只对其中k－2个比特进行硬判决，来计算目标比特的LLR。

例如b0，如图3，可以由b1、b2，b2、b3或者b1、b3的硬判决反馈结果。可能星座点分布的范围越大，目标比特的度量计算越准确。

图3 k－2比特反馈下b0对应星座点范围

经计算，b0和b1由b2、b3的硬判决反馈，b2由b0、b3的硬判决反馈，b3由b1、b2的硬判决反馈时可得到最佳效果。为了进一步减少运算量，可对式(3)运用log－max近似法［7］，即

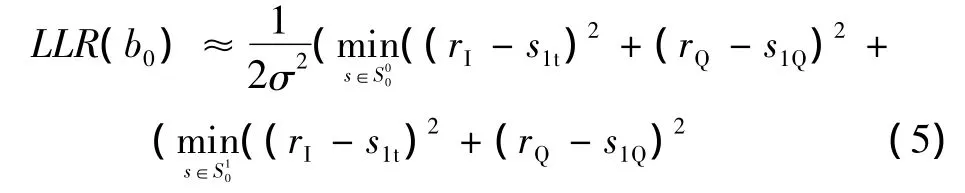
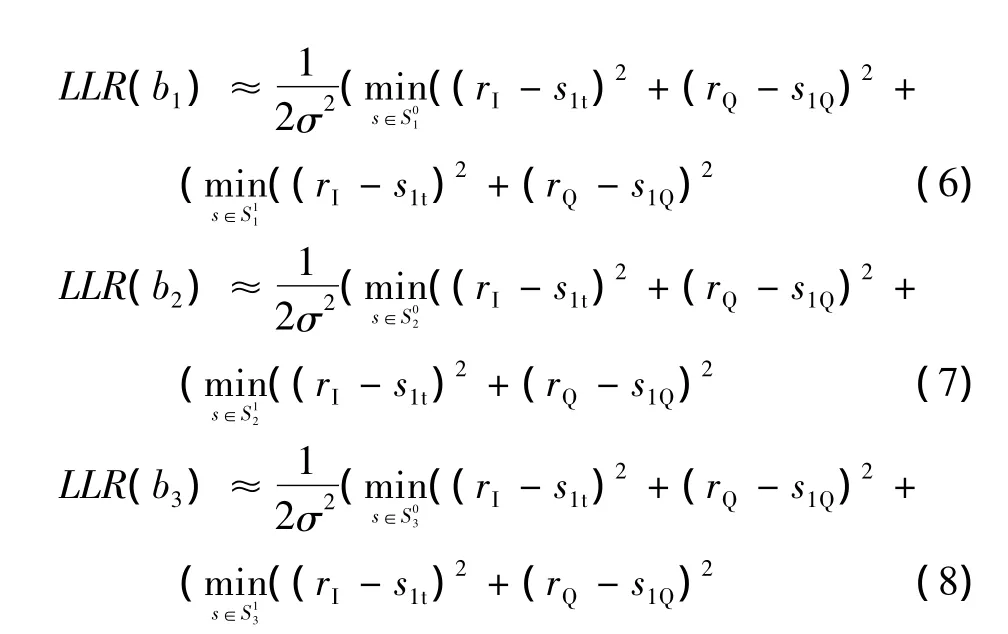
该方法相对于原来的迭代解映射增加了比较运算，却提高了解映射的准确率。总的来说，计算量没有大的提高。

3.2 基于判决边界的软信息

文献［6］中的GA解映射算法利用了迭代结构，降低了运算复杂度，但是在首次解映射中由于译码器无法进行反馈，仍需要用式(3)计算软信息。本文提出了改进算法2，根据硬解映射中的判决边界计算软信息，简化运算。

硬解映射运用符号与星座图中坐标间的逻辑关系，划分了若干个判决限，根据接收符号与判决边界的位置关系，进行硬判决得到各位比特结果［8］。本文基于判决边界，用接收符号与各比特判决边界间的坐标间距来表示该比特的LLR。以16QAM旋转星座为例，见图4。

图4 16QAM旋转星座的判决边界

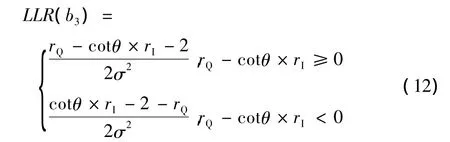
式中:θ为表1中的旋转角度。该算法避免了原方法首次解映射里的指数运算，主要是用加减计算，非常利于硬件实现。

表2列出16QAM调制下原方案与2种改进方法运算量比较。MPY是实数的乘法，ADD是实数的加法，CMP表示比较运算，JUD表示判决运算。由表中所见，改进算法1与原方案在运算复杂度上并没有太大的变化。而改进算法2与原方案相比，明显减少了运算量，当迭代次数增加时，解映射性能优势更加明显。

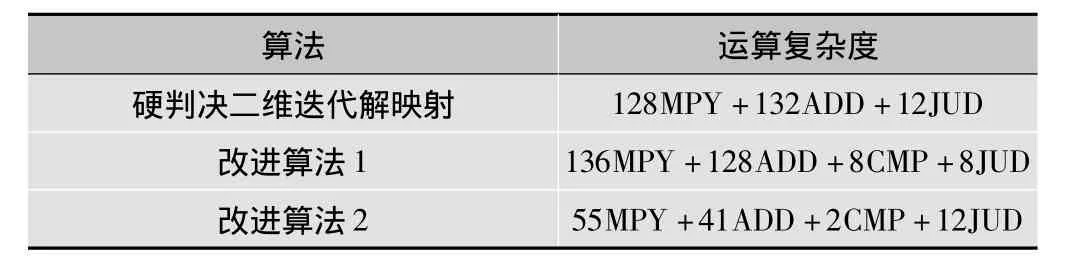
表2 改进算法与原算法复杂度比较

4 仿真结果

本文在DVB－T2标准下进行了计算机仿真，仿真条件如下:

1)LDPC编码采用2/3码率，帧长为64 800 bit;

2)星座映射方案采用16QAM调制，依据DVB－T2标准，旋转角度为 16.8°。

图5是在Rayleigh信道下对原方案和改进方法算法1的误码性能比较。由仿真结果可见，k－2比特反馈的误码率明显小于原来的二维迭代LLR解映射。结合表2，在计算复杂度没有大的改变下，误码性能得到明显提高。

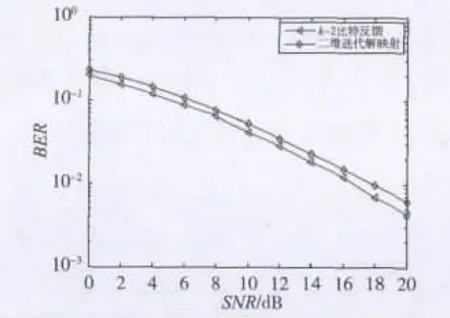
图5 改进算法1与二维迭代解映射BER性能比较

图6是在迭代次数为10时的误码仿真结果，信道条件为Ricean信道。虽然改进算法2与原来的二维迭代解映射算法在误码性能上存在一些差距，但在差距相对较小的情况下，计算复杂度明显降低，方便工程实现。

图6 改进算法2与二维迭代解映射BER性能比较

5 结论

本文从优化角度出发，综合系统性能和运算复杂度，对应用旋转星座的DVB－T2系统提出两种改进的解映射算法。第一种算法扩大解范围，寻找更优方案，在复杂度没有较大条件下改善解映射性能。第二种算法降低运算复杂度，节省资源，利于硬件实现。

［1］侯晔，潘长勇，杨昉.星座旋转及坐标交织在DTMB系统中的应用研究［J］.电视技术，2013，37(4):28－31.

［2］ YANG Feng，ZHANG Bo，DING Lianghui.Low complexity iterative demapping algorithm for rotated QAM constellations in DVB－T2 system［C］//Proc.2013 International Conference on Computing，Networking and Communications.San Diego，CA:IEEE Press，2013:424.

［3］ BOULLE K，BELFIORE JC.Modulation scheme designed for the Rayleigh fading channel［C］//Proc.CISS’92.Princeton，NJ:［s.n.］，1992:420－423.

［4］ VANGELISTA L，ROTOLONIM.On the analysis of P1 symbol performance for DVB－T2［C］//Proc.IEEE Sarnoff Symposium.Princeton，NJ:IEEE Press，2009:l－5.

［5］张博.DVB－T2中的关键技术研究以及部分模块设计［D］.上海:上海交通大学，2012.

［6］ HAFFENDEN O.DVB－T2:the common simulation platform［R］.［S.l.］:British Broadcasting Corporation，2011.

［7］何燕锋，杨鸿文，郭文彬.高阶调制的软输出算法比较［J］.北京邮电大学学报，2003，26(1):82－85.

［8］马卓，杜栓义，王新梅.BICM系统中一种低复杂度的迭代解映射算法［J］.西安电子科技大学学报，2011，38(2):42－46.