直剪作用下不共面断续节理岩桥破断试验与数值研究

赵延林，彭青阳，万 文，王卫军，赵伏军

（湖南科技大学 能源与安全工程学院；煤矿安全开采技术湖南省重点试验室，湖南 湘潭 411201）

工程岩体的破坏和失稳通常是由于在荷载作用下，岩体中断续节理的张开、闭合、起裂、扩展及贯通而产生新的剪切破断面所引起的［1－3］。在这些剪切破断面上除了原生结构面外，还包含原生节理间岩桥的破断面。岩体的破坏特征表现为原生节理和自节理端部扩展的岩桥断面所组成的复合破坏面［4－6］。研究断续节理岩桥张拉破坏的初裂机理与岩桥贯通机制对于探讨岩体工程的失稳及渐进破断机理具有重要理论意义［7－8］。

直剪试验可以很好地模拟断续节理岩体的受力状态，是研究断续节理扩展贯通的有效试验手段。目前大量的理论和试验工作集中在单轴或双轴试验研究，较少采用直剪试验研究［9－11］。通过分析断续节理的几何和力学特点，进行断续节理岩体直剪试验，研究断续节理扩展贯通规律，为探索断续节理岩桥破断提供了新的研究思路。直剪试验条件下，若节理全部分布在剪切平面内，为共面断续节理。若节理不全在剪切平面内，则为不共面断续节理。各国学者对剪切作用对共面断续节理破坏模式和力学机理进行了不少研究。Lajtai等［12］按法向应力的大小，将岩桥的破坏分为张拉、剪切和挤压破坏。朱维申等［13］对剪切面含3条节理的试样进行直剪试验，发现共面断续节理岩体存在剪胀和受剪上抬后转动现象。白世伟等［14］研究发现法向应力、节理的连通率、排列方式对共面断续节理岩体的贯通扩展有重要影响。刘远明等［15］在试验研究的基础上提出了直剪条件下共面断续节理岩桥力学性质弱化机制和岩桥贯通模型。目前对研究共面断续节理岩体较多，而对不共面断续节理岩体研究较少。Savilahti等［16］进行了2条不共面断续节理岩体直剪试验，发现岩桥的破断源于断续尖端，与节理面接近垂直的方向扩展并最终贯通。

直剪作用下断续节理岩桥的贯通破坏模式及其变形和强度特性在很大程度上受断续节理面的规模、密度和空间分布特征的控制，岩桥的倾角和长度将直接影响其变形和破坏机制。已有研究对共面断续节理的剪切破坏机理进行了大量实验和理论研究，而对于直剪作用下不共面节理的全剪切失效过程及强度特性的实验研究很少报道。笔者以不共面断续节理岩体为研究对象，以水泥砂浆作为类岩石材料，对不同排列分布的断续节理试件进行平面应力加载条件下的正、反向直剪试验，探讨直剪下不共面断续节理的岩桥破断方式和剪切全过程规律。并通过FLAC3D对岩桥破断机理、剪切破断面的形成过程进行数值研究，以揭示岩桥的拉裂破坏和破断面的剪切屈服机理。

1 试验材料与试验方案

1.1 试件制备

为研究直剪作用下岩桥的脆性破坏，试验采用与岩石相似（脆性、剪胀）的模型材料（由白水泥、沙子、水组成）制作类岩石模型试样，采用的模型材料配比为：白水泥∶沙子∶水＝26∶25∶10（重量比），沙子为粗细不同的两级清洁粒组（0.15～0.30 mm），试验模具采用钢制模具，其内部尺寸为：20cm×15cm×3cm。

将0.1mm厚的薄钢片按一定展布沿直剪方向预置于模具中央，将一定配比的水泥砂浆料浇注于模具，在室温下养护3～4h后，将擦拭机油的1mm厚钢片在预设直剪引导裂纹位置插入试件中以形成直剪引导裂纹，养护12h后，脱模，并将钢片抽出；试件脱模后，检查试件表面及端部平整度，并对裂纹的贯穿性进行检查，对出现形状不规整、端部不平的试件进行打磨，保证试件的不平整度满足试验要求；对于出现的破损试样进行剔除。将脱模后的试件放入自来水中养护28d。

1.2 不共面断续节理展布及试验设备

为研究直剪作用下不共面断续节理的岩桥断裂、贯通、剪切机理，在直剪面上布置多条断续节理以研究不同倾角、不同岩桥长度下不共面断续节理岩桥破断规律和强度特性。

试验采用断续节理长度b＝4cm，倾角α取15°、30°、45°、60°和90°，裂纹条数n取3、4、5条，每种试件各加工5组，并按一定规则将其编号，如SC4541表示裂纹倾角为45°，裂纹条数为4条的第1组试件。图1为不共面断续节理展布示意图。

图1 不共面断续节理展布示意图

直剪作用下不共面断续节理的岩桥破断试验在湖南科技大学岩石力学试验室的长春朝阳公司生产的RYL－600微机控制岩石伺服剪切流变仪上进行。试验机采用DOLI全数字交流伺服测试系统，压力长时间稳定度≤±2%，变形测量精度在±0.5%以内，可进行岩石材料的变角度剪切、三轴流变和结构面的直剪试验。直剪试验过程以0.5kN／s的速率（应力控制）施加预设法向荷载，固定法向力，以0.005mm／s的变形速率（应变控制）施加水平剪切力，直至试验破坏。用数码相机对断续节理的断裂、贯通、剪切全过程进行实时观测并视频输出。图2为正在RYL－600微机控制岩石伺服剪切流变仪进行直剪作用下不共面断续节理的岩桥破断试验图。

图2 直剪作用下不共面断续节理的岩桥破断试验

为研究不同剪切方向下不共面断续节理的岩桥破断规律，采用正向剪切和反向剪切两种不同的直剪模式对试件进行剪切试验。正向剪切和反向剪切加载方式见图3。

图3 正向剪切和反向剪切加载方式

2 直剪下不共面断续节理的强度特性

2.1 正向剪切下不共面断续节理全剪切过程

以裂纹倾角45°，含4条断续节理的试件（编号SC4541）为例，研究正向剪切下不共面断续节理的全剪切过程。图4为试件SC4541的全剪切曲线。正向剪切作用下受剪面的变形和破坏过程具有明显的阶段性，在一定压应力下，随剪应力的增加，试件经历线弹性阶段、断续节理尖端起裂扩展阶段、岩桥断裂贯通阶段、剪切面爬坡咬合阶段和残余摩擦阶段5个阶段。正向剪切下不共面断续节理全剪切过程强度特性如下：

图4 正向剪切下试件SC4541的全剪切曲线（α＝45°，n＝4）

1）剪切第1阶段——线弹性阶段。在一定的法向正应力下，随剪应力的施加，断续节理上、下表面发生相对位移，断续节理尖端拉应力集中，在裂纹尖端应力强度因子达到材料的断裂韧度之前，整个受剪面处于线弹性阶段，此时试件的弹性抗剪强度为S1。

2）剪切第2阶段——断续节理起裂扩展阶段。随剪应力的增加，节理面上多余能量将集中到裂纹尖端部位，使裂纹端部产生拉应力集中。当裂纹尖端应力强度因子达到材料的断裂韧度时，裂纹尖端出现拉剪型翼形裂纹，剪应力有小幅跌落，翼形裂纹稳定扩展，剪切承载能力并不因初裂而丧失。试验发现，靠近加载端的节理首先起裂，远离加载端的节理滞后起裂，此时试件的初裂抗剪强度为S2。

3）剪切第3阶段——岩桥断裂贯通阶段。随着翼形裂纹的扩展，靠近加载端的节理首先呈齿形贯通，远离加载端的节理贯通延迟，剪切承载能力下降，当破断面贯通时试件的贯通抗剪强度为S3。

4）剪切第4阶段——剪切面爬坡咬合阶段。剪切破断面贯通后，随剪应力的增加，剪切面爬坡咬合，剪切承载能力上升，试件抗剪强度达到峰值S4。

5）剪切第5阶段——残余摩擦阶段。当试体越过峰值强度，沿主破断面发生宏观整体的脆性剪断破坏后，其抵抗剪切荷载的能力迅速下降，仅依靠其破断面的摩擦阻力承担，试件进入残余摩擦阶段，此时试件残余抗剪强度为S5。

正向剪切作用下试件SC4541的全剪胀曲线见图5。图5表明随剪切位移的增加，试件法向膨胀，而产生剪胀位移，其剪胀效应在剪切面爬坡咬合阶段表现尤为显著，最大剪胀位移达5.24mm。

图6为正向剪切作用下试件SC4541的岩桥破断图。正向剪切作用下岩桥的破断形式为断续节理交错贯通搭接，最终形成齿形破断面。

2.2 反向剪切下不共面断续节理全剪切过程

图5 正向剪切下试件SC4541的全剪胀曲线（α＝45°，n＝4）

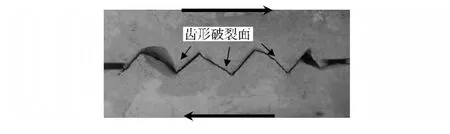
图6 正向剪切下试件SC4541的岩桥破断图（局部放大图）

图7为裂纹倾角45°，含4条断续节理的试件SC4542的反向剪切过程全曲线。反向剪切作用下受剪面的变形和破坏过程亦具有明显的阶段性。与正向剪切相似，反向剪切过程也经历线弹性阶段、断续节理起裂扩展阶段、岩桥断裂贯通阶段、破断面摩擦咬合阶段和残余摩擦阶段。

图7 反向剪切下试件SC4542的全剪切曲线（α＝45°，n＝4）

反向剪切加载初期，试件受剪面处于线弹性阶段，弹性抗剪强度为S1；当剪切位移达2.6mm左右时，试件初裂，断续节理尖端萌生平行于直剪方向的拉剪型裂纹，其初裂抗剪强度S2；随剪切位移的增加，在近直剪方向上拉剪裂纹将断续节理贯通，形成完整破断面，此时剪应力跌至最低值S3；由于摩擦作用以及破断碎块的咬合作用，剪应力回升，并达到峰值抗剪强度S4。此后在一定的正应力作用下，依靠破断面的摩擦力，抗剪强度在残余强度S5附近徘徊。随剪切位移的增加，试件的剪胀效应在断续节理起裂扩展阶段开始显现，在剪切面爬坡咬合阶段表现尤为显著，最大剪胀位移为3.92mm。图8为反向剪切下试件SC4542的全剪胀曲线。

图8 反向剪切下试件SC4542的全剪胀曲线（α＝45°，n＝4）

图9为反向剪切作用下试件SC4542的岩桥破断图。反向剪切作用下岩桥的破断形式表现为断续节理尖端萌生平行于直剪方向的拉剪裂纹（见图9（a）），图9（a）对应于图7中全剪切曲线上的A 点，处于岩桥断裂贯通阶段；拉剪裂纹将断续节理沿直剪方向贯通，最终形成带状破断面。伴随带状破断面的贯通形成，在加载端部由于局部应力集中而萌生剪切裂纹（见图9（b）），图9（b）对应于图7中全剪切曲线上的B点，处于摩擦咬合阶段。

图9 反向剪切下试件SC4542的岩桥破断图（局部放大图）

与正向剪切相比，反向剪切下节理的初裂抗剪强度、峰值抗剪强度较大。反向剪切下由于近直剪方向的拉剪裂纹的贯通，导致剪应力下降幅度远比正向剪切下裂纹贯通时的剪应力跌落幅度要小得多，反向剪切下的剪应力下降幅度为0.26MPa，仅为正向剪切下的剪应力跌落幅度的1／4。而且裂纹起裂至贯通过程中反向剪切的剪切位移行程远大于正向剪切的情况，反向剪切下完成拉剪裂纹贯通的剪切位移行程为2.87mm，其位移量是正向剪切情况下的5.08倍。这说明反向剪切下不共面续断节理的起裂扩展具有延性，拉剪裂纹的扩展、贯通不会导致试件抗剪强度的急剧下降。反向剪切下剪切面的摩擦咬合作用不及正向剪切，剪切承载能力上升幅度不大，但反向剪切下的峰值抗剪强度达到仍要大于正向剪切下的峰值抗剪强度。

2.3 裂纹倾角90°试件的全剪切过程

对裂纹倾角90°试件而言，正向剪切和反向剪切无区别，图10为法向应力为1.0MPa下含4条断续节理，倾角90°的试件SC9041的剪切全过程曲线。在法向应力1.0MPa下，当剪切位移达1.98mm左右时，试件初裂，节理尖端萌生平行于直剪方向的拉剪型裂纹，其初裂抗剪强度S2＝2.18MPa；随剪切位移的增加，在岩桥间出现斜切方向上的压剪裂纹，压剪破裂面和拉剪破裂面贯通，剪应力跌至最低值S3＝0.81MPa；随后由于破裂面的摩擦以及碎块咬合作用，剪应力回升，并达到峰值抗剪强度S4＝2.83MPa。由于破裂碎块的增加，其抗剪能力逐渐下降，剪切过程进入残余强度阶段。

图10 试件SC9041的全剪切曲线（α＝90°，n＝4）

图11为试件SC9041的岩桥破断演化图。在剪切过程中，首先在靠近加载端的裂纹尖端萌生平行于直剪方向的拉剪裂纹（见图11（a）），图9（a）对应于图10中全剪切曲线上的A点；随着剪切位移的增加，在岩桥间出现斜切方向上的压剪裂纹，最终试件形成压剪破裂面和拉剪破裂面贯通而失去承载力（见图11（b）），图11（b）对应于图10中全剪切曲线上的B点。

2.4 初裂抗剪强度、峰值抗剪强度的影响因素分析

表1为裂纹倾角α为15°、30°、45°、60°和90°，裂纹条数分别为3、4、5条的不共面断续节理试件在法向应力分别为1.0、2.0MPa下的平均初裂抗剪强度S2和峰值抗剪强度S4。

表1表明影响试件初裂抗剪强度S2、峰值抗剪强度S4的因素主要有：裂纹倾角α、法向应力σn和相邻节理搭接比例λ（λ＝b／e）。

表1 不同裂纹结构、法向应力下的平均初裂强度和峰值强度

定义剪切力施加方向沿逆时针与断续节理之间的夹角为断续节理剪切角β，如图12。正向剪切下断续节理剪切角β为裂纹倾角α，反向剪切下断续节理剪切角β＝180－α。

图12 断续节理剪切角β的示意图

图13为法向应力σn＝1.0MPa，4条断续节理试件在正向、反向剪切下试件的平均初裂抗剪强度S2、峰值抗剪强度S4与断续节理剪切角β的关系曲线。从图13看出，断续节理剪切角β对试件初裂抗剪强度S2和峰值抗剪强度S4影响显著。正向剪切下，随剪切角β（即裂纹倾角α）的增大，试件的初裂抗剪强度S2和峰值抗剪强度S4明显增加；在反向剪切下随剪切角β的增加（即裂纹倾角α的减少）试件初裂抗剪强度S2和峰值抗剪强度S4整体上呈减少趋势。反向剪切下，剪切角β＝165°（裂纹倾角α＝15°）时，初裂抗剪强度S2最小，剪切角β＝135°（即裂纹倾角α＝45°）时，初裂抗剪强度S2最大。剪切角β＝90°下，正向剪切和反向剪切相同，相比其它剪切角（β＝120°、135°除外），剪切角β＝90°下的初裂抗剪强度和峰值强度较大。

图13 平均初裂抗剪强度S2、峰值抗剪强度S4与断续节理剪切角β关系曲线

无论是正向剪切还是反向剪切，法向应力的存在显著地改变裂纹尖端的拉压状态，较高的法向应力导致裂纹尖端由受拉状态和受压状态转化，法向应力的增加导致初裂抗剪强度S2和峰值抗剪强度S4大幅增加。以裂纹倾角α＝45°，含4条断续节理的正向剪切试件为例，在法向应力σn＝1.0MPa下的平均初裂抗剪强度S2和峰值抗剪强度S4分别为1.67、1.99MPa，而σn＝2.0MPa下的平均初裂抗剪强度S2和峰值抗剪强度S4分别为2.56、3.27 MPa，后者分别是前者的1.53、1.64倍。

研究发现，相邻节理的距离对抗剪强度产生较大影响，引入相邻节理搭接比例λ，用下式表示：

式中：b为断续节理长度；e为相邻节理间水平距离。

图14为裂纹倾角α＝45°、法向应力σn＝1.0MPa下试件平均初裂抗剪强度S2、峰值抗剪强度S4与相邻节理搭接比例λ的关系曲线。图14表明，在试验的相邻节理搭接比例λ下，随λ的增加，正向剪切试件初裂抗剪强度S2和峰值抗剪强度S4均非线性增大，正向剪切试件则相反，随λ的增加，反向剪切试件初裂抗剪强度S2和峰值抗剪强度S4均非线性减小。

图14 初裂抗剪强度S2、峰值抗剪强度S4与λ的关系曲线

相邻节理搭接比例λ在一定程度表征了断续节理的分布密度，对于正向剪切试件而言，断续节理的初裂是由于断续节理的相对滑移，其尖端拉应力集中而起裂，其起裂角约为70.5°［17］，当λ增加时，裂纹间相互影响作用加剧，导致断续节理初裂抗剪强度增大［18－19］，剪切面破断贯通后进入爬坡咬合阶段，随λ的增加，其爬坡咬合愈强，从而导致试件的峰值抗剪强度S4随λ的增加而增大。对于反向剪切试件而言，拉剪翼形裂纹为近平行于直剪方向，随λ的增加，翼形裂纹的贯通路径缩短，试件初裂抗剪强度S2和峰值抗剪强度S4相应下降。

3 直剪下不共面断续节理岩桥破坏的数值试验

3.1 断续节理的接触单元模拟

从数值试验的角度探讨直剪下不共面断续节理的岩桥破坏机理，采用FLAC3D研究正向、反向直剪下不共面断续节理岩桥破坏规律。采用interface单元的Coulomb剪切模型模拟断续节理的滑移屈服和剪胀效应。图15为接触面本构模型示意图。对于Coulomb滑动的接触面单元存在相互接触和相对滑动。接触面相对滑动所需切向力Fsmax为：

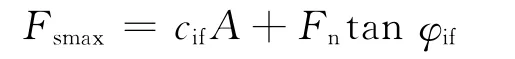
式中：cif为接触面的黏聚力；φif为接触面的内摩擦角；Fn为接触面的法向压力；A为接触面积。

图15 接触面单元本构模型的组成元件图

式中：σn0为修正前的法向应力；ψ为接触面的剪胀角；kn为节理法向刚度；为修正前的剪力大小。

当接触面的拉应力Ft超过抗拉强度时，接触面破坏，切向力和法向力均为0。

FLAC3D数值分析中用剪切软化模型 Mohr－Coulomb模拟类岩石材料（岩桥）的屈服破坏过程。

3.2 计算模型

通过对试验所用的水泥砂浆类岩石材料进行强度和变形测试，获得类岩石材料和节理的强度、变形参数，见表2。数值试验采用的类岩石材料剪切软化参数见表3。

表2 类岩石材料和节理的计算参数

表3 剪切软化参数表

直剪下不共面断续节理的数值试验模型尺寸：20cm×15cm×3cm，裂纹长度b＝4cm，倾角α分别为15°、30°、45°、60°和90°，裂纹条数n 取3、4、5条。针对不同的节理分布和法向应力下进行近40次数值试验。

下面以裂纹倾角α＝45°、含4条断续节理试件在法向应力σn＝1.0MPa作用下的情况为例，研究正向、反向剪切下不共面断续节理的岩桥破断特性。其计算模型的力学边界条件和加载方式见图16。正向剪切方向从左至右，沿图示实线方向加载；反向剪切方向从右至左，沿图示虚线方向加载。

3.3 结果分析

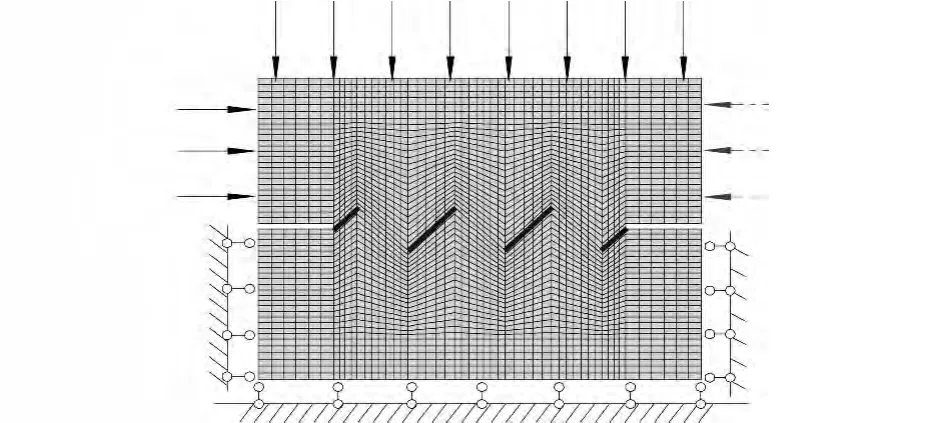
图16 计算模型的边界条件和剪切加载方式

3.3.1 正向剪切 图17为数值试验得到的正向剪切下不共面断续节理的全剪切曲线。通过数值曲线和试验曲线对比分析（图17），发现数值试验的峰值抗剪强度比试验值偏大，数值曲线的峰后剪切应变软化效应比试验曲线显著，但总体上数值曲线和试验曲线在走向和量值上仍吻合。选取数值曲线上的1＃、2＃、3＃的3个特征点，跟踪数值曲线的1＃、2＃、3＃特征点时岩桥的塑性区演化，得到不同剪切阶段的岩桥破断规律见图18。

从图18可以发现，在加载初期，随剪切位移的增加，断续节理尖端萌生拉裂单元（见图18（a）），对应于数值曲线上的1＃特征点；随剪切位移的发展，拉裂单元逐渐贯通，靠近加载端节理首先贯通，远离加载端的节理滞后贯通，这与试验结果相吻合（见图18（b）），此时对应于数值曲线上的2＃特征点；岩桥拉裂贯通后，岩桥进入剪切滑移阶段，试件抗剪承载力上升达到峰值抗剪强度，图18（c）为峰值抗剪强度时的岩桥塑性区分布（对应于数值曲线上的3＃特征点）。图18（c）显示了伴随岩桥破断，断续节理全部剪切屈服。

图17 正向剪切下数值曲线和试验曲线对比分析

图18 正向剪切下不同剪切阶段岩桥破断规律（局部放大图）

3.3.2 反向剪切 图19为反向剪切下数值曲线和试验曲线的对比。通过跟踪数值曲线的1＃、2＃特征点时岩桥塑性区演化，得到反向剪切下不同剪切阶段的岩桥破断规律见图20。

从图20可以看出，在加载初期，断续节理尖端萌生拉裂单元（见图20（a），对应于数值曲线上的1＃特征点）；随剪切位移的发展，拉裂单元和剪切屈服单元将断续节理贯通，峰值抗剪强度时岩桥内形成一条近带状的屈服单元（见图20（b），对应于数值曲线上的2＃特征点），伴随岩桥破断，断续节理发生受剪屈服和受拉破坏。

图19 反向剪切下数值曲线和试验曲线对比分析

图20 反向剪切下不同剪切阶段岩桥破断规律（局部放大图）

4 结论

1）直剪作用下不共面断续节理岩桥破坏过程具有明显的阶段性，经历线弹性阶段、裂纹起裂扩展阶段、岩桥断裂贯通阶段、剪切面爬坡咬合阶段和残余摩擦阶段5个阶段。

2）直剪下断续节理尖端的拉剪应力状态决定了节理岩体的初裂抗剪强度，而贯通剪切面的爬坡咬合效应决定了节理岩体的峰值抗剪强度；影响试件初裂抗剪强度、峰值抗剪强度的主要因素有裂纹倾角、法向应力、相邻节理搭接比例。

3）正向剪切下岩桥呈齿形破断面，反向剪切作用下岩桥表现为沿直剪方向贯通的带形破断面，与正向剪切相比，反向剪切下裂纹的初裂抗剪强度和峰值抗剪强度较大。

4）直剪下不共面断续节理岩桥破断的数值试验从力学机理上解释了正向剪切下齿形破断面和反向剪切下带状破断面的形成过程，揭示了岩桥的拉裂破坏和破断面的剪切屈服机理。

［1］朱维申，李术才，陈卫忠.节理岩体破坏机理何锚固效应及工程应用［M］.北京：科学出版社，2002.

［2］刘远明，夏才初.直剪条件下非贯通节理岩体岩桥力学性质弱化机制及贯通模型初步研究［J］.岩土力学，2010，31（3）：695－701.Liu Y M，Xia C C. Weakening mechanism on mechanical behaviors and failure models of rock mass containing discontinuous joints in direct shear ［J］.Rock and Soil Mechanics，2010，31（3）：695－701.

［3］Shen B，Stephansson O，Einstein H H，et al.Coalescence of fractures under shear stress in experiments ［J］.Journal of Geophysical Research，1995，100（B4）：5975－5990.

［4］范景伟，何江达.含定向闭合断续节理岩体的强度特性［J］.岩石力学与工程学报，1992，11（2）：190－199.Fan J W，He J D.Strength properties of intermittently joints rockmass ［J］. Chinese Journal of Rock Mechanics and Engineering，1992，11（2）：190－199.

［5］唐志成，夏才初，丁增志.非贯通类节理岩体剪切变形规律分析［J］.岩土力学，2011，32（8）：2344－2358.Tang Z C，Xia C C，Ding Z Z.Analysis of shear deformation law for intermittent jointed rock mass［J］.Rock and Soil Mechanics，2011，32（8）：2344－2358.

［6］刘刚.非连续岩体破裂机理及其工程稳定性研究［D］.徐州：中国矿业大学，2009.

［7］高保彬，高佳佳，袁东升.基于UDEC的大采高覆岩破裂的模拟与分析［J］.湖南科技大学学报：自然科学版，2013，28（2）：1－6.Gao B B，Gao J J，Yuan D S.Simulation and analysis of overlying strata fracture in large mining height top－coal caving face of coal seams based on UDEC ［J］.Journal of Hunan University of Science ＆Technology：Natural Science Edition，2013，28（2）：1－6.

［8］王敏，万文，赵延林，等.压剪条件下岩体剪切力研究［J］.矿业工程研究，2013，28（3）：53－56.Wang M，Wan W，Zhao Y L，et al.The shear stress study of rock mass under compression－shear ［J］.Mineral Engineering Research，2013，28（3）：53－56.

［9］Bobet A，Einstein H H.Fracture coalescence in rocktype materials under uniaxial and biaxial compression［J］.International Journal of Rock Mechanics and Mining Sciences，1998，35（7）：863－888.

［10］Sagong M，Bobet A.Coalescence of multiple flaws in a rock－model material in uniaxial compression ［J］.International Journal of Rock Mechanics and Mining Sciences，2002，39：229－241.

［11］赵延林，万文，王卫军，等.类岩石材料有序多裂纹体单轴压缩破断试验与翼形断裂数值模拟［J］.岩土工程学报，2013，35（11）：2097－2109.Zhao Y L，Wan W，Wang W J，et al.Fracture experiments on ordered multi－crack body in rock－like materials under uniaxial compression and numerical simulation of wing cracks ［J］.Chinese Journal of Geotechnical Engineering，2013，35（11）：2097－2109.

［12］Lajtai E Z.Shear strength of weakness planes in rock［J］.International Journal of Rock Mechanics and Mining Sciences ＆ Geomechanics Abstract，1969，6（7）：499－515.

［13］朱维申，梁作元，冯光北，等.节理岩体强度特性的物理模拟及其强度预测分析［C］／／计算机方法在岩石力学及工程中的应用国际学术讨论文集.武汉：武汉测绘科技大学出版社，1994：486－493.

［14］白世伟，任伟中，丰定祥，等.共面闭合非贯通岩体强度特性直剪试验研究［J］.岩土力学，1999，20（2）：10－16.Bai S W，Ren W Z，Feng D X，et al.Research on the strength behavior of rock containing coplanar close intermittent joints by direct test ［J］.Rock and Soil Mechnics，1999，20（2）：10－16.

［15］刘远明，夏才初.共面闭合非贯通节理岩体贯通机制和破坏强度准则研究［J］.岩石力学与工程学报，2006，25（10）：2086－2091.Liu Y M，Xia C C.Study on fracture mechanism and criteria of failure strength of rock mass containing coplanar close discontinuous joints under direct shear［J］. Chinese Journal of Rock Mechanics and Engineering，2006，25（10）：2086－2091.

［16］Savilabti T，Nordlund E，Stephansson O.Shear－box testing and modeling of joint bridge［C］／／Barton N R，Stephansson O.Proceedings of International Symposium for Rock Joints，Norway，1990：295－300.

［17］Ashby M F，Hallam S D.The failure of brittle solids containing small cracks under compressive stress states［J］.Acta Metallurgica，1986，34（3）：497－510.

［18］赵延林，万文，王卫军，等.类岩石裂纹压剪流变断裂与亚临界扩展实验及破坏机制［J］.岩土工程学报，2012，34（6）：1050－1059.Zhao Y L，Wan W，Wang W J，et al.Compressiveshear rheological fracture of rock－like cracks and subcritical crack propagation test and fracture mechanism ［J］. Chinese Journal of Geotechnical Engineering，2012，34（6）：1050－1059.

［19］任中俊，陈跃欣.有限大平板中心裂纹应力强度因子分析［J］.矿业工程研究，2013，28（4）：1－3.Ren Z J，Chen Y X.Investigation of stress factor of centre crack in finite plate ［J］.Mineral Engineering Research，2013，28（4）：1－3.