直流牵引供电网暂态电路模型与参数分析

李夏青 王奎鹃

（1. 北京石油化工学院电气工程系 北京 102617 2. 北京化工大学 北京 100029）

1 引言

直流牵引供电系统的短路故障是威胁供电系统运行安全的主要因素。由于发生短路故障的随机性和不可预知性，使故障原因查找、故障机理分析等工作更多地依赖于牵引供电系统的电磁暂态模型。

牵引供电系统的电磁暂态模型由电源、牵引网和负荷模型组成。目前，普遍采用一阶 RL电路的暂态过程作为牵引供电系统的电磁暂态模型，并基于此模型设置了电流变化率与电流增量暂态保护（dI/dt-ΔI保护）；文献[1]从分析直流牵引供电系统故障录波的波形特征入手，指出直流牵引供电系统的电磁暂态模型不能用一阶 RL电路的零状态响应模型等效；文献[2]讨论了射频电磁波在隧道内的传输、衰减特性，分析了隧道尺寸等因素对射频电磁波传播的影响；文献[3]分析了直流牵引网泄漏电流的分布特性，以及美国、欧洲地铁的轨道电位限制标准问题；文献[4]研究了直流牵引供电系统储能电容的效率及其对供电系统的影响；文献[5]研究了架设于地面的电气化铁路工频交流接触网的电磁场分布特性，但未考虑隧道的影响；文献[6]建立了直流牵引供电系统的电源与负荷的等效模型；文献[7]研究了牵引网的稳态电路参数，未研究隧道对牵引网电路参数的影响。总之，对直流牵引供电系统的稳态模型的研究较多，对牵引网的暂态特性的研究较少；在为数不多的有关直流牵引供电系统电磁暂态特性的文献中，有关电磁暂态模型的研究较多，缺少对隧道内牵引网电路参数的系统研究，致使直流牵引供电系统电磁暂态模型存在缺陷，使保护系统不得不采用“宁可误动，不可拒动”的整定原则，造成供电系统误动率居高不下，降低了牵引供电系统的可靠性。

本文针对牵引供电系统电磁暂态模型的“短板”（隧道内牵引网等效电路元件的暂态特性表述）问题，建立了物理模型，解决了直流牵引网的暂态电阻、电感、电容的建模与求解问题。

2 直流牵引网等效电路模型

2.1 直流牵引网

直流供电牵引网是沿地铁（或矿山）线路敷设并为电动车辆提供电能的专用装置。牵引网由正极接触轨和负极走行轨构成，如图1所示。

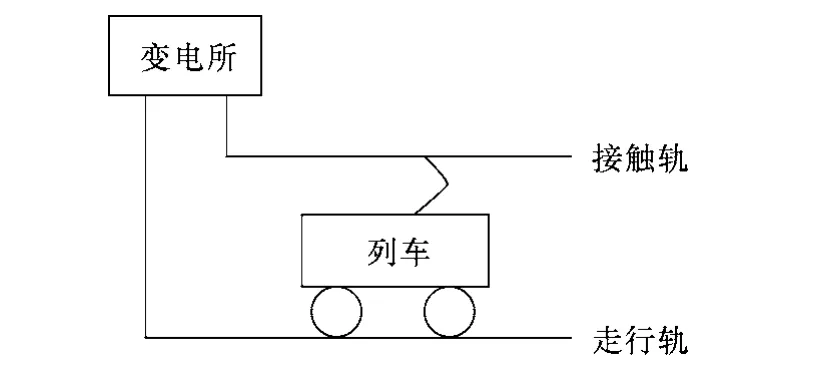
图1 牵引网示意图Fig.1 Diagram of traction power supply net

对于采用三轨供电方式的牵引网，由于正极接触轨布置在隧道侧面，使隧道内电磁场呈不对称分布，导致牵引网等效电路元件的求解困难，截面图如图2所示。

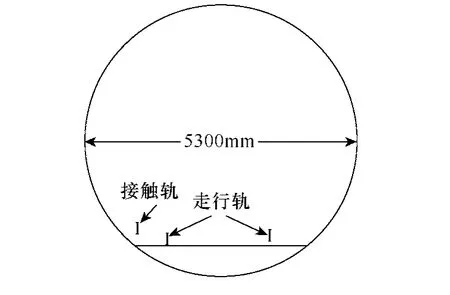
图2 隧道截面图Fig.2 Cross-section of subway tunnel

2.2 牵引网等效电路模型

运行实践表明，在牵引网发生短路故障或运行状态发生改变时，牵引网的电流会出现剧烈的变化如图3和图4所示，故需考虑牵引网的暂态特性，图5为牵引网等效电路的暂态模型。

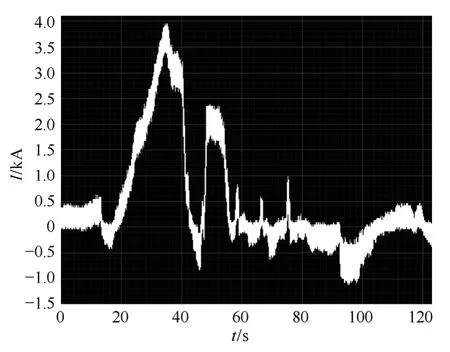
图3 负荷电流Fig.3 Original records of traction load current

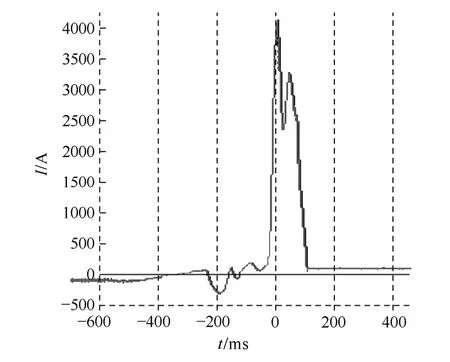
图4 故障录波Fig.4 Current waveform of short-circuit test

图5中，牵引网的回路电阻R由接触轨电阻R1和走行轨电阻 R2、R3组成；过渡电阻 Rg是走行轨与隧道壁之间的电阻。

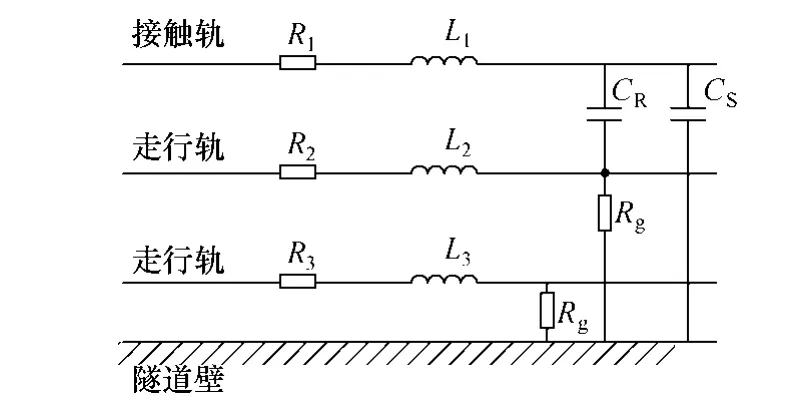
图5 牵引网暂态等效电路Fig.5 Transient equivalent circuit on traction power supply net

牵引网的电感：牵引网的接触轨、走行轨的电感L1、L2、L3由各自的内自感Ln和外自感Lw构成；外自感 Lw包括接触轨与走行轨之间的电感 LR和接触轨（走行轨）与隧道壁之间的电感Ls。

牵引网的电容 C：由接触轨与走行轨之间的电容和CR接触轨与隧道间的电容CS构成。

3 元件模型与算法

3.1 元件建模的共性问题

3.1.1 接触轨、钢轨的简化计算模型

接触轨、钢轨为不规则截面导体，用具有相同横截面积的圆柱形导体等效接触轨、钢轨，以简化计算的复杂性。表1所示为轨条截面几何参数。

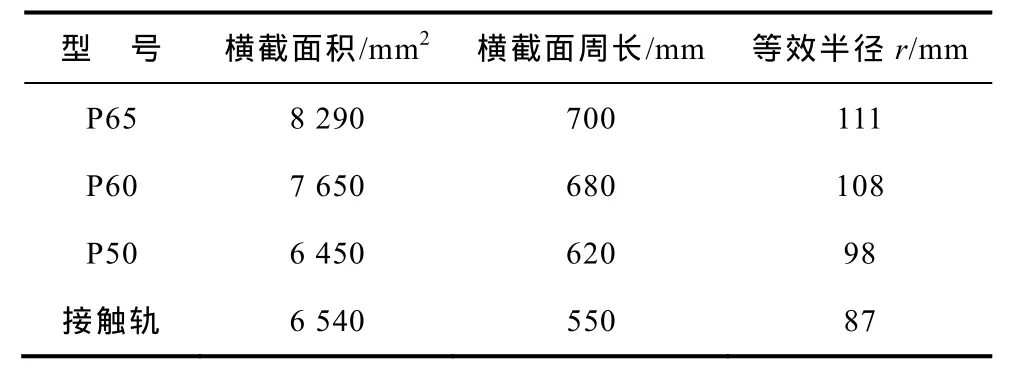
表1 轨条截面几何参数Tab.1 Geometry parameters of rail

在图 6中，r1为接触轨等效截面半径，r2、r3为钢轨等效截面半径，d12、d13、d23为轨道间距。

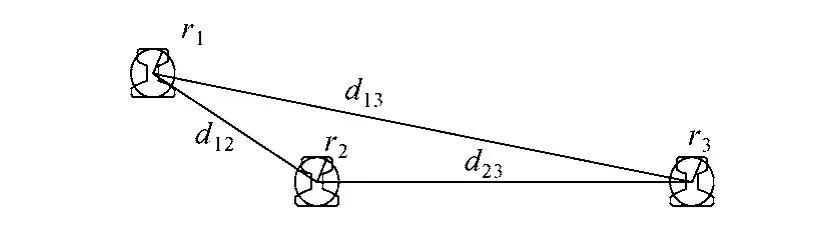
图6 轨道间距Fig.6 Gauge of rail

3.1.2 趋肤效应与磁导率

牵引网负荷电流（见图 3）变化缓慢（变化周期约 20～30s）；牵引网故障电流（见图 4）变化较快，其频谱主要成分为直流和低于 30Hz的交流分量（表2）。根据文献[8]的研究结果，直径较大的导体，当电流频率超过 10Hz时，需考虑趋肤效应对电阻、电感计算值的影响问题。密（为增强隧道的强度）之特点，将隧道壁等效为半径为 Rl的金属空心圆柱；接触轨（或走行轨）等效为套在空心圆柱内的半径为R2的金属圆柱，且两柱轴线平行并相距d，如图7所示。

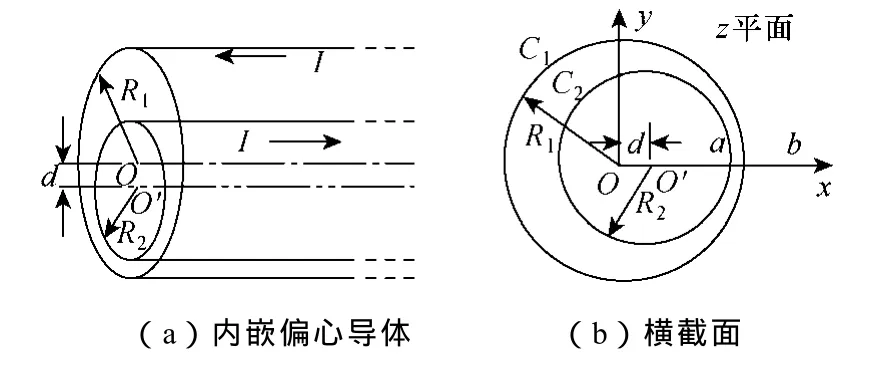
图7 内嵌偏心导体结构Fig.7 Embedded eccentric center conductor

（2）保角映射。为使用安培环路定律计算牵引网三条轨道对隧道壁的外自感及电容，需将图 7b中z平面上的圆C1、C2变换为两个同心圆。在图7b中，设z平面上的点a和b的坐标分别为 x1和 x2，且点a、点b同时关于圆C1、C2对称，则由对称点的定义[10]得

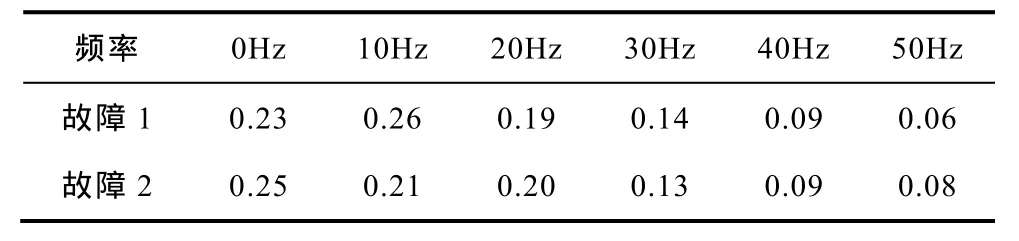
表2 故障电流频谱Tab.2 Fault current spectrum

钢轨由铁磁性材料构成，根据文献[9]的实验结论，需考虑钢轨磁导率随电流变化的非线性影响。

3.1.3 内嵌偏心导体的保角映射模型

地铁（或矿山）隧道为钢筋混凝土结构，因牵引网位于隧道一侧（见图2），使隧道内电磁场呈不对称分布，为计算牵引网三条轨道对隧道壁的外自感和电容，建立了“内嵌偏心导体的保角映射”模型，具体方法如下。

（1）内嵌偏心导体结构。根据隧道结构钢筋很

将点a变换为ζ平面的原点ζ＝0，点b变换为ζ平面的无限远点 ζ＝∞。根据分式保角变换的性质，z平面上的圆 C1变换为 ζ平面上的圆C1'；同理，圆C2变换为 ζ平面上的圆C2'，且圆C1'和圆C2'为同心圆，如图8所示。

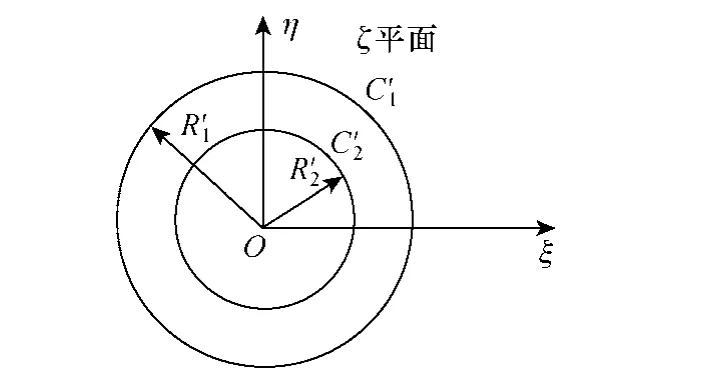
图8 映射后的两同心圆Fig.8 Conformal mapping result

分别取z等于R1、R2，由式（3）可求得圆的半径为

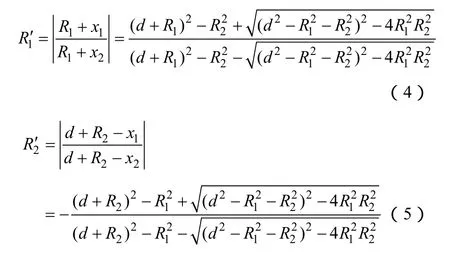
3.2 回路电阻和过渡电阻

3.2.1 回路电阻

不考虑趋肤效应影响时，牵引网电阻为直流电阻

由表2知，牵引网电流主要由直流、10Hz、20Hz和30Hz的交流成分组成。根据文献[8]的研究结果，对于半径接近100mm的接触轨和走行轨，当电流频率超过10Hz时需考虑趋肤效应的影响。定义10Hz电流为基频电流 I1，其电阻为R1=R0，20Hz、30Hz的电流为2次、3次谐波电流。根据文献[11]的分析，h次谐波电阻与基波电阻的关系为

由能量守恒定律得牵引电流在轨条等效电阻Req上的总损耗为

3.2.2 过渡电阻

根据中华人民共和国行业标准 CJJ49—92[12]走行轨与隧道壁之间的过渡电阻Rg取3Ω/km；接触轨与隧道间为绝缘状态，接触轨与隧道间的电阻可视为“∞”。

3.3 牵引网电感

3.3.1 钢轨、接触轨的内自感

考虑到钢轨、接触轨的等效半径及相对磁导率均较大，在计算钢轨、接触轨的内自感时需考虑趋肤效应的影响[8,9]。由此得接触轨、钢轨的单位长度内自感为

式中，μ=μ0μr为接触轨、钢轨的磁导率；ber、bei为贝塞尔函数的实部（Bessel Real）、虚部（Bessel Imaginary）；ber'和bei'分别为 ber和 bei的一阶导数，δ为趋肤深度；f为电流频率；γ为电导率。3.3.2 不考虑隧道影响时牵引网的外自感

对图6所示的轨道间距，设各条走行轨中的电流为接触轨电流的 1/2，采用三平行导线模型可得不考虑隧道影响时牵引网的外自感为

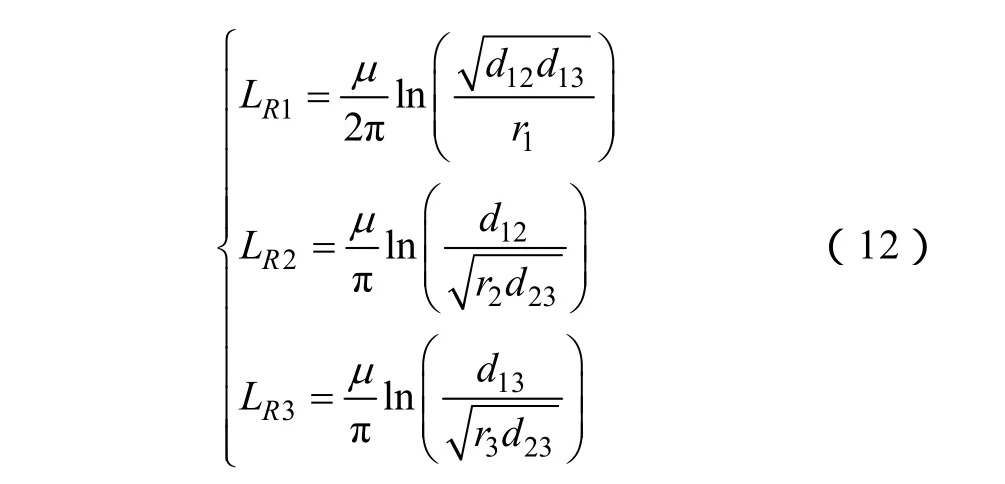
3.3.3 牵引网相对隧道壁的外自感

由图2可见，接触轨、走行轨距隧道中心的间距相近，且接触轨、走行轨的等效半径亦相差不大（表1），所以，经“内嵌偏心导体保角映射模型”变换后所得的同心圆半径R2'基本相同；接触轨与走行轨中电流的流向相反，根据安培环路定律，两同心圆间的磁场是由接触轨与走行轨的电流差产生的，故仅需计算三根轨条中的一根与隧道壁间的外自感。

对图8，设内外圆柱体上的电流均为I，则由对称性和安培环路定律得磁场强度的大小为

由磁能公式 W=(1/2)LI2得牵引网相对隧道壁的外自感为

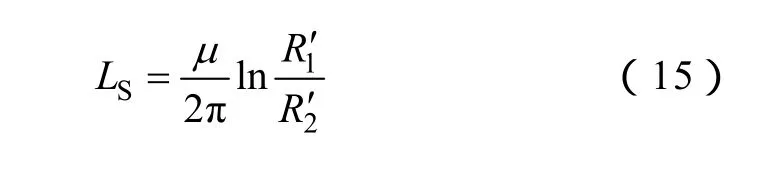
3.3.4 牵引网电感

从图5可见，两根走行轨为并联关系；接触轨与隧道壁构成一个回路，接触轨与走行轨构成另一个回路，两条回路的互感效应纳入接触轨的外自感LS，则牵引网电感为

式中

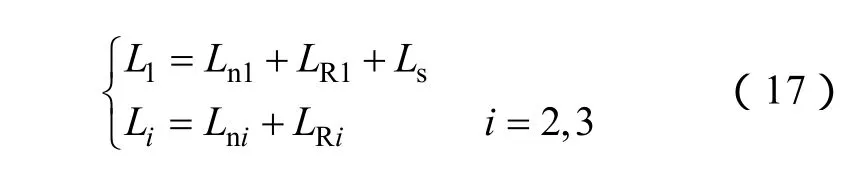
3.4 牵引网电容

接触轨相对走行轨的电容可使用二平行线模型求得

式中，C1i为接触轨对走行轨 2、3的电容；r1为接触轨的等效半径。

由于走行轨与隧道间的过渡电阻Rg较小，可认为走行轨与隧道壁等电位，故只需考虑接触轨与隧道间的电容。按照“内嵌偏心导体保角映射模型”求得接触轨与隧道间的等效电容为

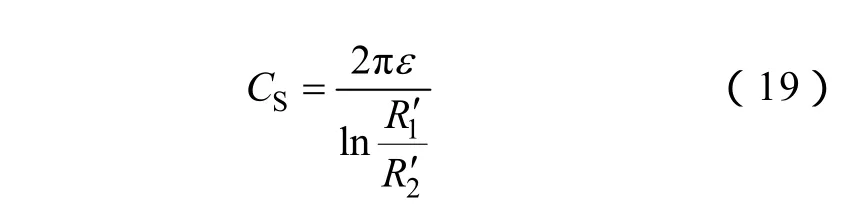
牵引网电容为

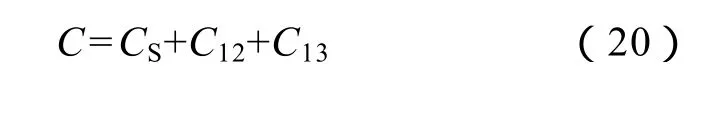
4 算例

按照北京地铁隧道内牵引网的安装图，牵引网各轨条中心间距为 d12=684mm、d13=2176mm、d23=1 505mm；隧道半径R1=2 650mm；轨条中心距隧道中心的距离d=2 000mm。

4.1 钢轨电阻

按式（9）和式（10），得到表3所示轨道单位长度电阻值。

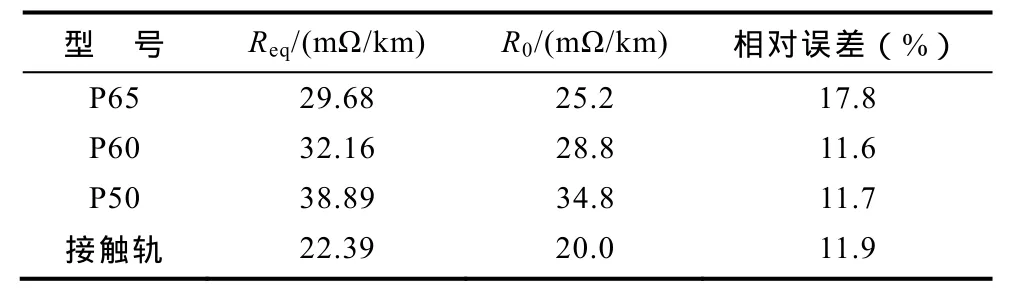
表3 轨条电阻Tab.3 Resistance of rail

4.2 牵引网电感

按式（11）～式（17）计算牵引网的电感。为便于与测量值比较，表 4～表 6所给数值均为 50Hz电流的计算值，图9给出了P50钢轨内自感随频率、电流的变化关系。

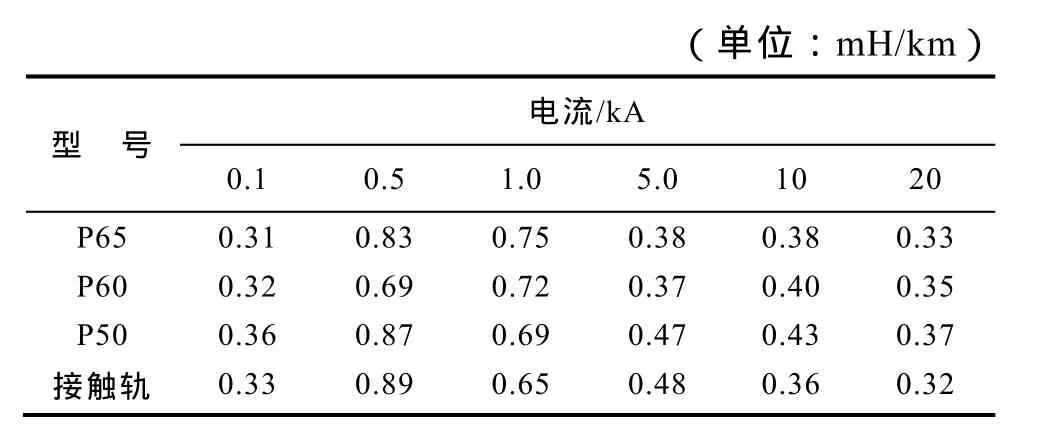
表4 轨条内自感Tab.4 Internal inductance of rail

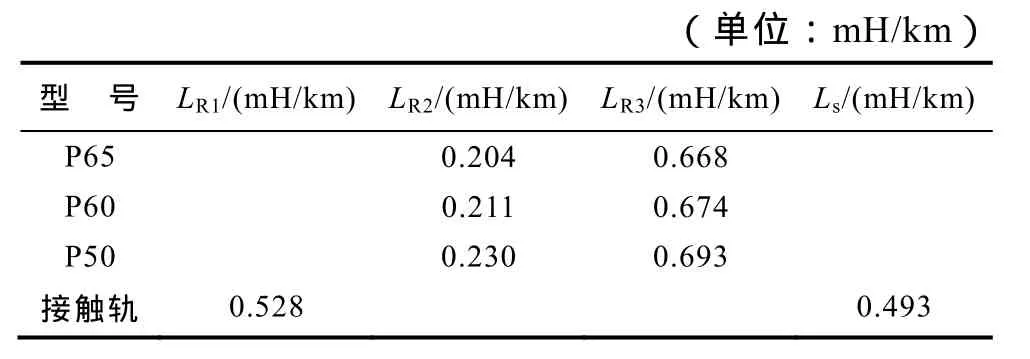
表5 轨条外自感及隧道电感Tab.5 External inductance

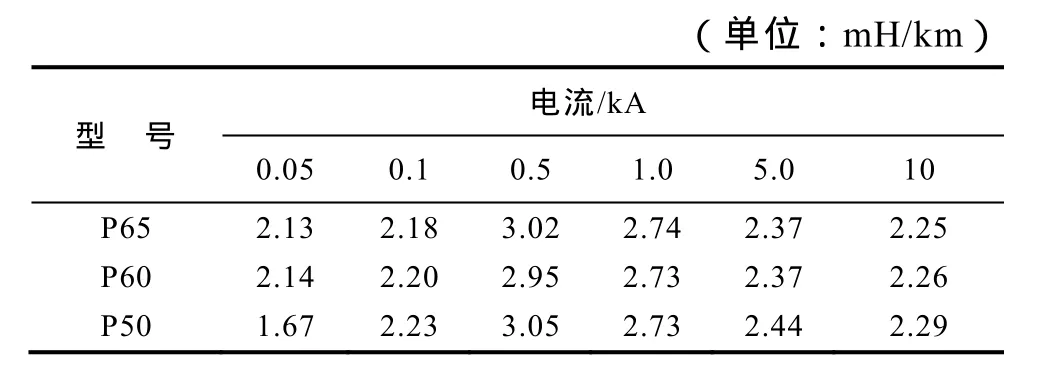
表6 牵引网电感Tab.6 Inductance of traction power supply net

4.3 牵引网电容

按式（18）和式（19）计算牵引网电容结果见表 7。

表7 牵引网电容Tab.7 Capacitance of traction power supply net

针对使用较为普遍的牵引网（采用P50钢轨作为走行轨），表8给出了电流为直流、交流f=50Hz，电流I=50A条件下的计算值和测量值。

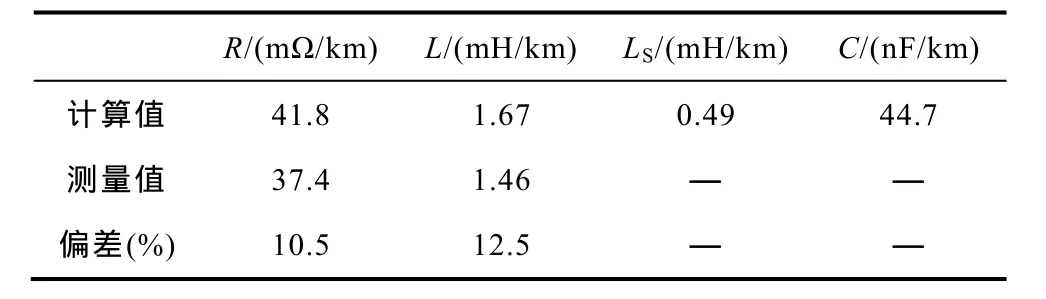
表8 参数对比Tab.8 Comparing with parameters of measure and calculate

5 讨论

（1）牵引网电阻。从表8可见：故障瞬间牵引网电流的交流成分使牵引网等效电阻值大于牵引网的直流电阻测量值，其相对偏差高于10%。

（2）牵引网电感与电流频率、电流强度的关系。构成牵引网电感的各成分中，内自感与电流频率、电流强度相关，图9给出了内自感与电流频率、电流强度的关系曲线。从图9和表4可见，电感的峰值出现在I=500～1 000A范围，且随电流频率的升高而降低。

图9 内自感与电流、频率关系Fig.9 Curve of internal inductance

（3）隧道电感 LS是难以测量且不容忽略的重要分量。由表 5可见，隧道电感 LS与 LR1、LR2、LR3的数值相当，其作用不容忽略。但从隧道空间尺寸及磁场强度计算式（式（13））可见，欲测量隧道电感LS，需提供足够大的测量电流，通常使用的阻抗测量法的测量电流为AC50Hz，I=10A～30A，不足以产生测量隧道电感LS的磁场强度，其测量值为不考虑LS影响的牵引网电感值，且该测量值与计算值接近（见表8）；牵引网短路瞬间，短路电流可达数千安乃至上万安培，综合考虑 LS、LR1、LR2、LR3与地铁 VVVF列车的储能滤波电容所构成的 RLC二阶电路[1]，其振荡频率与图 4波形的周波时间吻合，表明忽略 LS的影响将导致牵引供电系统电磁暂态模型失真严重。

（4）牵引网电容。由表7可见，牵引网电容C远小于电感、电阻之值，其影响可忽略。

6 结论

牵引网是直流牵引供电系统电磁暂态模型中的重要组成部分，通常使用阻抗测量法确定其等效电阻、电感之值，由于测量条件限制，所获得的测量值为接触轨与走行轨的稳态值，不能反映故障瞬间的等效参数，导致所建电磁暂态模型不能正确描述直流牵引供电系统的暂态特性。

本文针对地铁隧道和三轨供电牵引网的特殊结构，建立了内嵌偏心导体的保角映射模型和牵引网等效电阻模型，该模型物理概念清晰，计算方法简便，有效解决了直流牵引网的暂态电阻、电感、电容的建模与求解问题。

[1] 李夏青, 左丽. 直流牵引网故障电流能量谱及特征矢量[J]. 电工技术学报, 2010, 25(11): 164-168.Li Xiaqing, Zuo Li. Energy spectrum and eigenvector of DC traction power supply short-circuit current[J].Transactions of China Electrotechnical Society, 2010,25(11): 164-168.

[2] 李继生. 地铁隧道电磁波传输特性的研究[J]. 天津科技大学学报, 2005, 20(1): 34-36.Li Jisheng. Propagation characteristic of the electromagnetic waves in railway’s tunnels[J]. Journal of Tianjin University of Science and Tchnlogy, 2005,20(1): 34-36.

[3] Stell R W Benjamin. Maximum permissible rail potential: DC traction power systems[J]. IEEE Vehicular Technology Magazine, 2011, 6(3): 99-105.

[4] Baranov L A, Brodskii, Yu A, et al. Estimation of efficiency of stationary capacitor storage in subway based on experimental measurements of the operation of traction power-supply system[J]. Electrical Engineering, 2010, 81(1): 42-44.

[5] 赵震. 不同供电方式铁路电牵引系统工频电磁场计算与分析[D]. 北京: 铁道部科学研究院, 2001.

[6] 鲁彦青, 李夏青. 牵引供电系统建模与短路电流的仿真[J]. 北京石油化工学院学报, 2008, 16(3): 26-30.Lu Yanqing, Li Xiaqing. Simulation modeling of traction power supply system and the short circuit current[J]. Journal of Beijing Institute of Petrochemical Technology, 2008, 16(3): 26-30.

[7] 曾晶晶, 吴命利. 轨道电参数的稳态计算[J]. 中国电力, 2001, 3(6): 41-43.Zeng Jingjing, Wu Mingli. Steady-state calculation of electric parameters for rail transportation[J]. Electric Power, 2001, 34(6): 41-43.

[8] Omar M O Gatous, J Pissolato Filho. A new fomulation for skin-effect resistance and internal inductance frequency-dependent of a solid cylindrical conductor[C]. IEEE/PES Transmission & Distribution Conference& Exposition: Latin America, 2004: 919-924.

[9] Friedrich Kiebling, Rainer Puschmann, Axel Schmieder.Contact lines for electric railways[M]. Erlangen:Publicis Kommunikations Agentur GmbH GWA, 2000.

[10] 西安交通大学高等数学教研室. 复变函数[M]. 4版.北京: 高等教育出版社, 1996.

[11] 吕润余. 电力系统高次谐波[M]. 北京: 中国电力出版社, 1998.

[12] 中华人民共和国行业标准. CJJ49-92地铁杂散电流腐蚀防护技术规程[S]. 北京: 中国计划出版社,1993.