基于低秩矩阵填充的XLPE电力电缆寿命评估

许 刚 谈元鹏 黄 琳

（华北电力大学电气与电子工程学院 北京 102206）

1 引言

近年来，随着国家电网建设的持续发展，交联聚乙烯（Cross-Linked Polyethylene，XLPE）电力电缆被广泛应用于城市电网建设中。与油纸绝缘电缆相比，XLPE电力电缆具有生产周期短、安装工艺简便、抗高温、防腐蚀等优点。然而，随着运行时间的推移，早期投运的XLPE电力电缆由于受热老化、局部放电、电树枝、水树枝和机械损伤等因素的影响发生了绝缘老化[1,2]，导致电缆提前接近原设计使用寿命的终点，给电网的安全运行带来重大隐患。若无选择地对所有电缆进行检测，这将会是一个费时费力、耗资巨大的工程[3]。因此，对在役XLPE电力电缆进行寿命评估，预测电缆的剩余寿命已成为当前最重要的课题之一。

目前，国内外对 XLPE电力电缆的寿命评估方法大多偏向于对单一检测指标的分析。通过分析加速热老化拉伸断裂实验[4]、加速热延伸实验[5]、局放测量实验[6,7]、等温松弛电流实验[8]、差示扫描量热实验[9]、分步加压击穿实验[10]及直流泄漏电流实验[11]等电缆检测实验所测得的实验数据与电缆寿命之间的线性或非线性关系，实现对XLPE电力电缆定性或定量的寿命评估。基于单一检测指标的电缆寿命评估方法的研究，也有学者提出考虑多种检测指标的电缆寿命综合评估方法来提高寿命评估的精度，如模糊综合评定法[12]及神经网络法[13]等。然而，在现实生产实践中，由于各厂家与检测机构对电缆的检测条件不同，相关检测设备较为复杂昂贵，导致大多数电缆样本的检测指标类别并非完全相同。由于上述传统的电缆寿命综合评估方法要求电缆样本之间的检测指标类别相同，这就导致来自不同厂家与检测机构的部分样本与检测指标得不到有效利用，对现有的XLPE电力电缆检测资源造成了极大浪费。同时，这种小样本情况也为XLPE电力电缆寿命评估带来巨大挑战，使得传统的电缆寿命评估方法效果不佳甚至失效。

为应对传统算法所不能处理的电缆样本检测指标类别不统一导致的小样本寿命评估问题，本文提出一种基于低秩矩阵填充技术，并适用于部分电缆检测指标缺失的XLPE电力电缆寿命评估方法。该方法能有效利用现有的电缆检测指标，在对缺失的电缆检测指标信息进行恢复的同时，实现对目标电缆样本精确、定量的寿命综合评估。

2 基于低秩矩阵填充的电缆寿命评估方法

2.1 电缆寿命评估问题重述

在对电缆样本寿命进行评估时，设电缆样本的绝缘状态检测指标向量与其寿命yi∈R所构成有序对存在映射T:RM→R，使得yi=T(xi)，其中M为电缆样本的绝缘状态检测指标的类别数量，N为厂家与检测机构的数量，，fj为第j项电缆检测指标的数据预处理函数，为对第i个电缆样本的第j项检测指标的第k项检测数据。传统的电缆寿命综合评估正是从已有数据中分析、挖掘这一映射关系后，应用该映射关系对目标电缆样本进行寿命评估的。但正如上文中所述，在现实生产实践中，大多数电缆样本的检测指标类别并非完全相同，即电缆检测指标信息是不完整的、缺失的，如图1所示。

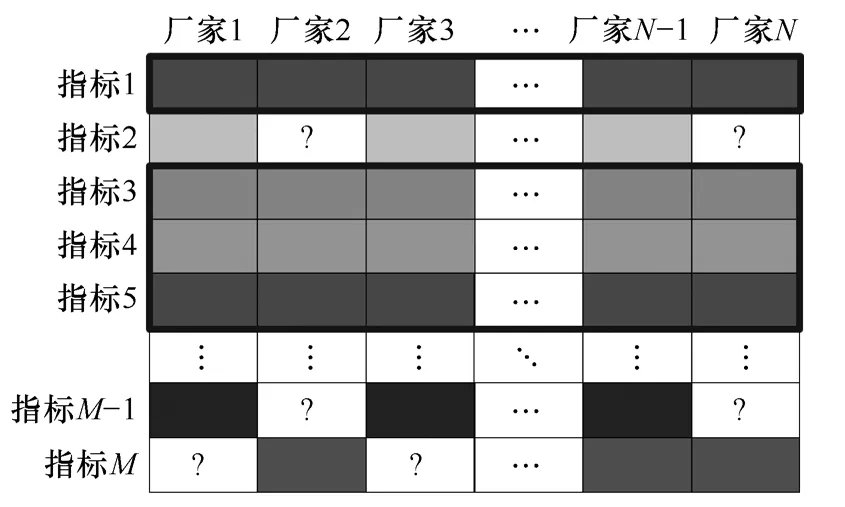
图1 电缆检测指标信息缺失示意图Fig.1 Schematic diagram of missing information on cable test categories

图1所示表格中的行坐标为检测指标类型，列坐标为厂家类别，带“？”标记的白色格子表示因厂家不能检测相应指标而导致的数据缺失。传统的电缆寿命综合评估方法使用所有厂家共同具有的检测指标类别（如图1中粗线框所示的指标1、指标3、指标4及指标5等）进行寿命评估，余下的检测指标（如图1中指标2、指标M-1及指标M）的信息将被丢弃。然而，若能利用这部分被丢弃的信息对缺失信息进行恢复，则可能达成更高精度的寿命评估。若将缺失的指标信息xij的值标记为0，则可得到一个包含所有样本的所有指标信息的受损矩阵，而缺失信息的恢复则可看作是该受损矩阵的填充问题。值得注意的是，若电缆样本的绝缘状态检测指标与寿命满足线性相关性，则电缆样本信息所构成的受损矩阵可被看做一个受损的低秩矩阵，其填充问题可由低秩矩阵填充技术进行求解。更进一步的，参考文献[14,15]，在应用低秩矩阵填充技术对缺失信息进行恢复的同时，也可实现对目标电缆的寿命评估。

2.2 低秩矩阵填充原理

矩阵填充技术（Matrix Completion，MC）主要研究了如何通过已知的部分矩阵元素来恢复整个矩阵这一问题。一般来说，满足要求的矩阵有无穷多个。然而，若原始信息矩阵D是一个受损的低秩矩阵，则可通过优化方法将其唯一分解为一个完好的低秩矩阵A与一个稀疏的噪声矩阵E之和，从而实现对原始信息矩阵D的精确恢复。对该受损矩阵D进行恢复的优化问题可表述如下

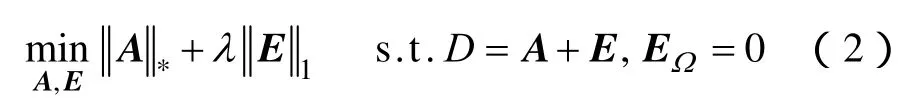
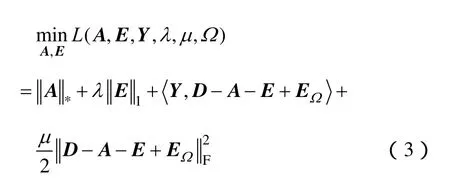
式中，μ为不可行点惩罚因子，μ＞0。参考文献[18]，则可通过迭代的方式对增广拉格朗日乘式优化问题进行求解（详见算法1）。

2.3 基于低秩矩阵填充的电缆寿命预测模型

若所研究的电缆样本的绝缘状态检测指标的总类别为M，则对于已知寿命的N1个电缆样本（即训练集）的绝缘状态检测指标向量RM∈可建立训练集检测指标矩阵，i=1,2,…,N1。由于不同电缆样本所测试的绝缘状态检测指标并不一定完全相同，易知训练集检测指标矩阵Xtr中存在若干零元素。将N1个电缆样本的寿命yi∈R写为一行，则可得到训练集寿命矩阵。同理，对于需要进行寿命估计的N2个电缆样本（即测试集）的绝缘状态检测指标向量（zi1,zi2,...,ziM）T∈RM，也可建立测试集检测指标矩阵，i=1,2,…,N2。同样地，测试集检测指标矩阵Xte也会存在若干零元素。建立零矩阵作为测试集寿命矩阵。则原始信息矩阵D可记为

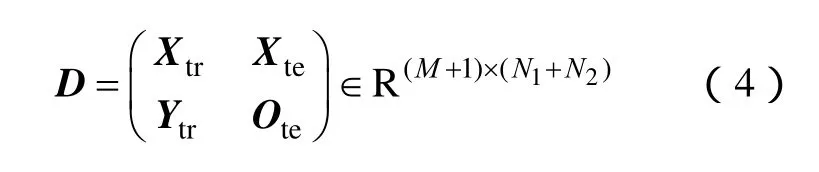
将原始信息矩阵D中非零元素的位置记为Ω。则部分检测指标缺失的电缆寿命预测问题就转化为2.2节中提到的受损矩阵恢复问题，可通过对式（3）所示的优化问题的求解求得N2个电缆样本的寿命进行评估。具体算法步骤如下所示。

输入训练集的绝缘状态检测指标与寿命iR∈y，i=1,2,…,N1；测试集的绝缘状态检测指标向量，i=1,2,…,N2；惩罚因子λ＞0；不可行点惩罚因子μ＞0；收缩步长ρ；收敛阈值ε；并初始化。

（2）为实现对原始信息矩阵D的填充修复，依照以下步骤实施，直到收敛：

通过特征值分解和算子收缩方法求解

输出测试集电缆样本的预测寿命AΛ。

值得注意的是，只有当电缆样本所测试的绝缘状态检测指标与老化时间或剩余寿命满足线性相关性时，样本之间绝缘状态检测指标向量才能表现出显著的相关性，即原始信息矩阵才能被认定为受损的低秩矩阵。为保证绝缘状态检测指标与老化时间或剩余寿命满足线性相关性，本文还需要在利用MC-LP算法进行寿命预测之前，对电缆检测数据做如下所示的预处理。

3 电缆检测实验数据的预处理方法

本文分别讨论了对于加速热老化拉伸断裂实验[4]、加速热延伸实验[5]、差示扫描量热实验[9]、分步加压击穿实验[10]及直流泄漏电流实验[11]等 5种电缆检测实验所测得的检测数据的预处理方法。通过对电缆检测实验所测得的检测数据进行相应的预处理，可使得若目标试样的电缆检测指标能被N1个训练样本的电缆检测指标，(i=1,2,…,N1)线性表示为

时，目标试样的相对老化时间sR能被N1个训练样本的相对老化时间(i=1,2,…,N1)线性表示为，即保证了绝缘状态检测指标与相对老化时间满足线性相关性。由于在MC-LP算法中可通过添加全1行向量的方式来保证，因而只需相对老化时间与电缆检测数据xij之间满足即可。

3.1 加速热老化拉伸断裂实验

电缆的温度场与电场之间存在近似的线性关系[19]，影响着电缆的老化速率与其相对老化寿命。因而，在通过绝缘材料加速热老化的方式对电缆寿命进行评估时，常会采用在 Arrhenius公式基础上的热寿命方程进行分析[4]。热寿命方程式（5）为

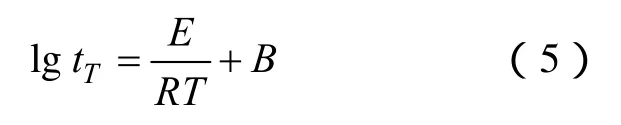
式中，tT为电缆绝缘材料在老化温度T下的使用寿命；E为绝缘材料的活化能，kJ/mol；R为摩尔气体常数，数值为8.314J/(mol·K)；B为与绝缘材料性能相关的常数。可将式（5）记为

式中，a、b分别为与目标电缆类型绝缘材料及该类型电缆绝缘材料失效标准有关的常系数，a=E/R，b=B。因而，在固定的老化温度T下，电缆绝缘材料的使用寿命为。通过呈等差级数的热老化周期对同类型新电缆绝缘材料进行热老化，并测得不同老化时间下电缆试样的断裂伸长率信息。根据最小二乘原理及电缆试样的断裂伸长率信息，也可求得式（6）中a与b的值，记为与。则在老化温度T下电缆绝缘材料的使用寿命的值为。

若实验中以断裂伸长率作为寿命评估特征，将XLPE电力电缆绝缘材料的哑铃试件放置在不同的温度下加速热老化，并对不同老化时间下取出的试样进行机械拉伸实验。在固定的老化温度T下，依据文献[4]的数据结果，设断裂伸长率p与老化时间sT之间呈线性关系

式中，kT、cT为与老化温度T相关的系数。若令老化温度T下电缆绝缘材料的老化时间sT与使用寿命tT做比较，则可得到与老化温度T无关的相对老化时间为

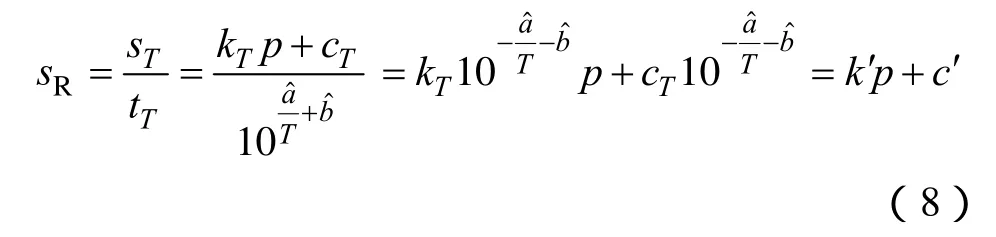
式中，k'、c'为与老化温度T无关的常系数，因而，断裂伸长率p与相对老化时间sR满足线性相关性。

3.2 加速热延伸实验

XLPE电缆绝缘材料的交联程度一般均以热延伸这一技术参数来间接衡量，因而，XLPE电缆绝缘材料的热延伸率可在很大程度上反映出电缆的使用寿命，尤其是当电缆在高温下使用时就显得更加重要。若实验中以热延伸率作为寿命评估特征，则需对比新电缆试件和老化电缆试件的负载伸长率及冷却后的永久伸长率，以判断XLPE电缆的老化程度。

将XLPE电缆绝缘材料的哑铃试件放置在烘箱中加速热老化，并对不同老化时间下取出的试样进行负载伸长率及冷却后永久伸长率的测量。试件应悬挂在烘箱中，试件下端添加重物以提供 20N/cm2的拉力。当烘箱温度迅速回升至规定温度200℃时，令试件在烘箱中保持加热状态15min后，测量哑铃试件中部标记线间的距离并计算负载伸长率ηh。从试件上解除拉力并将试件留在烘箱中恢复5min，并从烘箱中取出试件使之慢慢冷却至室温，再次测量哑铃试件中部标记线间的距离并计算永久伸长率ηc。在固定的老化温度T下，本文使用山东某电缆有限公司的出厂电缆测试数据，见表1。

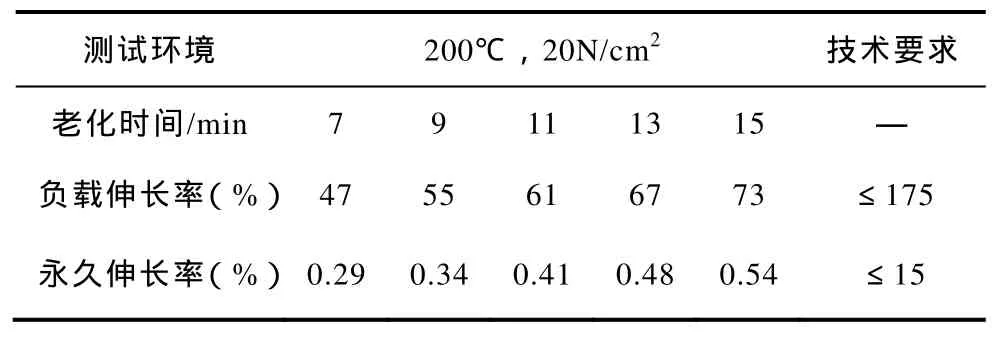
表1 110kV XLPE电力电缆热延伸检测指标Tab.1 Hot set test indicators of 110kV XLPE power cable

设负载伸长率ηh及永久伸长率ηc分别与老化时间sT之间呈线性关系

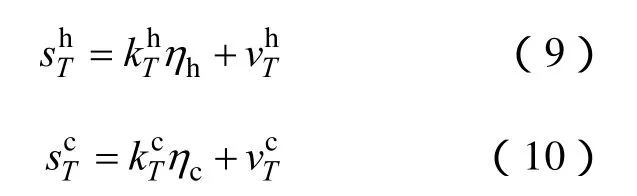
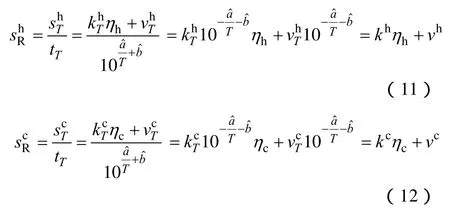
式中，kh、vh、kc、vc均为与老化温度T无关的常系数，，。因而，负载伸长率ηh及永久伸长率ηc分别与相对老化时间满足线性相关性。

3.3 差示扫描量热实验

差示扫描量热法（Differential Scanning Calorimetry，DSC）是在程序控制温度下，测量输给目标样本和参比物的功率差与温度关系的一种技术。DSC试验中，在目标试样和参比物试样容器下装有两组补偿加热丝，当试样在加热过程中由于热效应与参比物之间出现温差ΔT时，通过差热放大电路和差动热量补偿放大器，使流入补偿电热丝的电流发生变化。当目标试样吸热时，补偿放大器使试样一边的电流立即增大；反之，当目标试样放热时则使参比物试样一边的电流增大，直到两边热量平衡，温差ΔT消失为止。换而言之，目标试样在热效应时产生的热量变化因及时输入电功率而得到了补偿，因而，实验记录的应是目标试样和参比物试样下面两只电热补偿的热功率之差的峰值出现时间。若升温速率恒定，实验就仅需考虑出峰温度T*与老化时间s之间的对应关系即可。同样地，对XLPE电力电缆绝缘材料的试样放置在不同的温度下加速热老化，并对不同老化时间下取出的试样进行DSC测量。

在固定的老化温度T下，依据文献[9]的数据结果，设出峰温度T*与老化时间sT之间呈线性关系

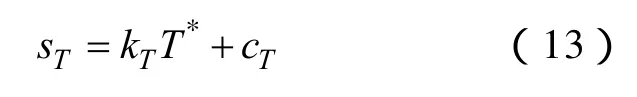
式中，kT、cT为与老化温度T相关的系数。若令老化温度T下电缆绝缘材料的老化时间sT与使用寿命tT做比，则可得到与老化温度T无关的相对老化时间sR∈[0,1]为

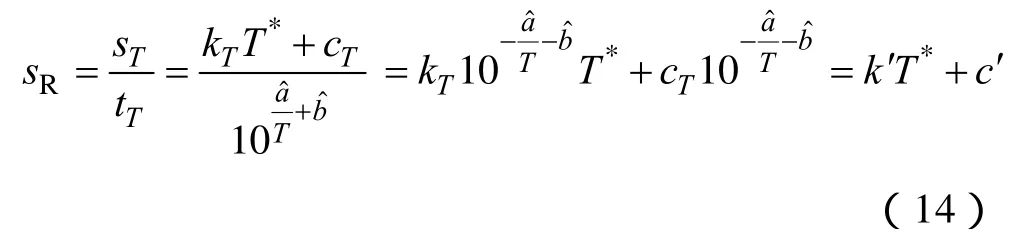
式中，k'、c'为与老化温度T无关的常系数，。因而，出峰温度T*与相对老化时间sR满足线性相关性。

3.4 分步加压击穿实验

分步加压击穿法进行电缆的寿命评估是指针对XLPE电力电缆寿命指数的研究，从经验寿命方程出发，通过采用近似简化法等获取寿命指数的数值，进而获得电缆的寿命。XLPE电缆的寿命方程[10]为

式中，U为电缆上所施加的电压等级；n为生命时间指数；t为电缆绝缘材料的使用寿命；c为常系数。实验采用分步加压法，相邻电压等级的比值为q=1.1。将试样分为两个实验组，分别在每个电压等级持续t1=1min和t2=20min，则有

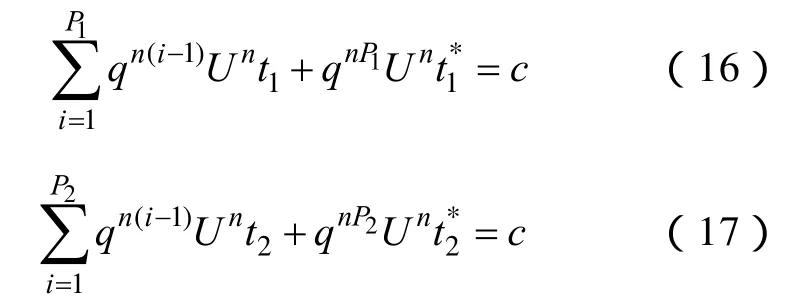
式中，P1、P2分别为两组达到击穿电压等级所需的级数；、分别为两组在最后一级达到击穿电压等级的加压时间。若设==0，经过一系列的数学推导可得出n值的计算公式为

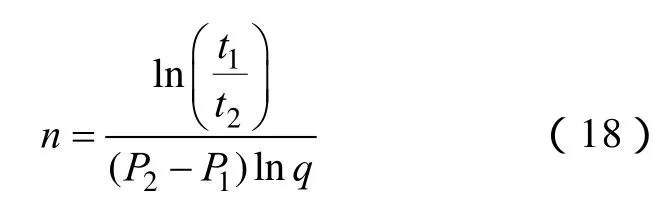
依照以上实验方法，首先，对新出厂的 XLPE电缆样本进行分步加压击穿实验，测得新电缆样本的生命时间指数n0，进而根据电缆在额定电压等级U0下的设计使用寿命，计算得出。其次，对目标XLPE电缆样本进行分步加压击穿实验，测得老化电缆样本的生命时间指数，则可根据电缆的真实工作电压等级计算得出电缆的相对老化时间sR∈[0,1]为

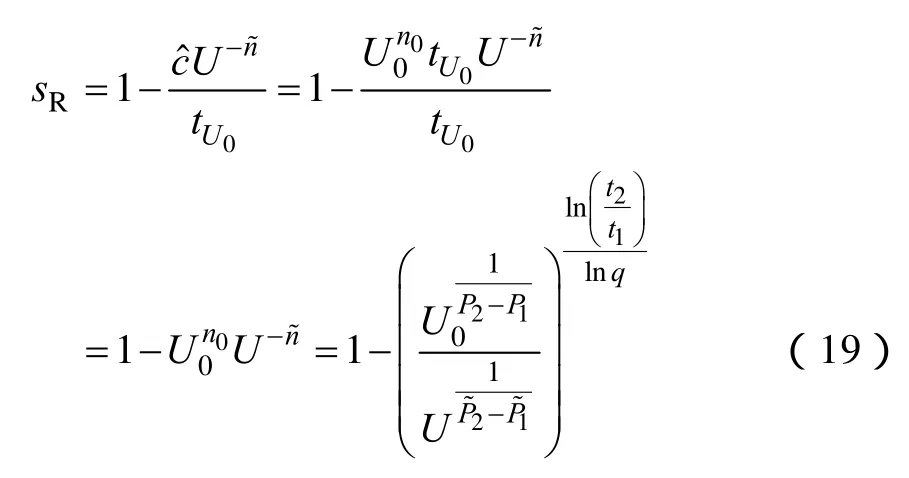
式中，P1、P2分别为两组新电缆样本达到击穿电压等级所需的级数；、分别为两组老化电缆样本达到击穿电压等级所需的级数。因而，与相对老化时间sR满足线性相关性。

3.5 直流泄漏电流实验

直流泄漏电流实验是通过在长度为l的电缆导体内芯上施加直流电压Ui，测试经过绝缘层到电缆外部包覆的金属屏蔽层的泄漏电流IG，从而计算电缆的单位长度绝缘电阻值R=RXl=Ui(IG·l)。实验中，从目标电缆上截取一段长度为l的电缆作为试样，并在试样的中央部分包覆屏蔽层。屏蔽层可由金属编织或金属带构成，其包覆的有效长度至少为1m，在有效长度的两端留出1mm的间隙，再绑扎5mm宽的金属丝作为保护环。之后，将试样弯成直径约为15d，（d为绝缘线芯的外径）但至少为0.2m的圆圈。试样应先置于试验温度T的空气烘箱中持续加温2h，再利用电压-电流法测电缆导体内芯和屏蔽层之间的绝缘电阻，原理如图2所示。此外，为使测量所得的绝缘电阻值基本稳定，进行电压-电流法测试时的充电时间应不少于1min。

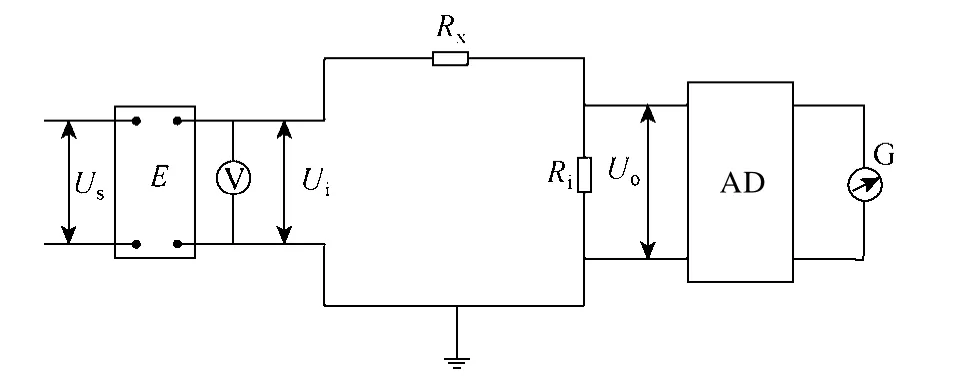
图2 电压-电流法测试原理图AD—高阻抗直流放大器E—直流电源 G—检流计或微安表Rj—直流放大器输入电阻Rx—试样绝缘电阻Us—交流输入电源电压Ur—直流输出电压Uo—放大器输入电阻压降 V—直流电压表Fig.2 Schematic diagram of current-voltage test

在固定的老化温度T下，依据文献[11]的数据结果，设单位长度绝缘电阻R与老化时间sT之间呈线性关系

式中，kT、cT为与老化温度T相关的系数。若令老化温度T下的电缆绝缘材料的老化时间sT与使用寿命tT做比，则可得到与老化温度T无关的相对老化时间sR∈[0,1]为

式中，k'、c'为与老化温度T无关的常系数，。因而，单位长度绝缘电阻R也与相对老化时间sR满足线性相关性。

4 仿真实验与结果分析

本文所有仿真实验均使用Core-TM i3-M330@2.13GHz处理器在Matlab 2012a环境下进行。MC-LP算法的惩罚因子取λ=0.15，不可行点惩罚因子取μ=0.85，收缩步长为ρ=0.995，收敛阈值为ε=0.05。本文实验所采用的22kV XLPE电力电缆样本的真实工作电压等级为22kV，工作环境温度T为90℃，设计使用寿命tT为30年。式（6）所示的热寿命方程中常系数a与b的值分别为=1424.50，=-9.98。仿真实验使用了22kV XLPE电力电缆样本在加速热老化拉伸断裂实验、加速热延伸实验、差示扫描量热实验、分步加压击穿实验及直流泄漏电流实验等5种电缆检测实验中测得的实验数据，并以山东某电缆有限公司的真实测试数据（见表2）为中心点，依照高斯分布生成45个训练集样本、15个测试集样本进行试验。

将单个训练样本与测试样本的断裂伸长率、负载伸长率、永久伸长率、DSC出峰温度、击穿实验折算指标及单位长度绝缘电阻等6个绝缘状态检测指标的数值均作为一个列向量形成一个矩阵，并随机对其中的50个元素强制赋值为0，且使每列上的零元素的数量不超过2，则可得到一个部分检测指标缺失的电缆绝缘状态检测指标信息矩阵(Xtr,Xte)∈R6×60。将训练样本的相对老化时间写为一个行向量Ytr∈R1×45，并生成一个全零的行向量Ote∈R1×15来对测试样本的相对老化时间进行评估。对原始信息矩阵D添加全1行向量1T∈R1×60来保证绝缘状态检测指标与相对老化时间满足线性相关，则可得到原始信息矩阵。应用MC-LP算法对原始信息矩阵D进行求解，可得测试集电缆样本的相对老化时间。依据测试集中第i个电缆样本的真实投运时间，易知其寿命应为。

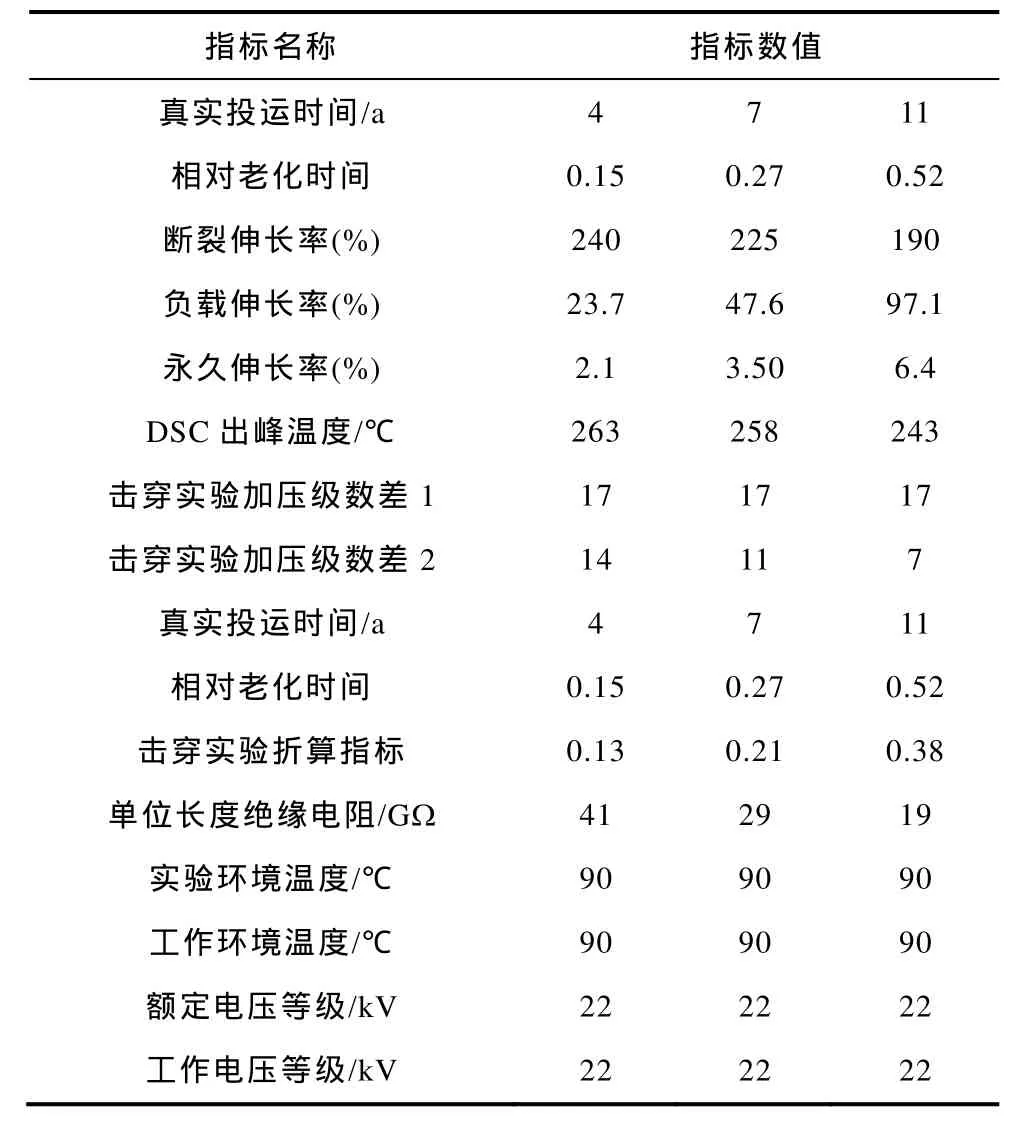
表2 22kV XLPE电力电缆绝缘状态检测指标Tab.2 Insulating state test indicators of 22kV XLPE power cable

为避免实验结果的随机性，本文应用 MC-LP算法及神经网络误差反向传播（Error Back Propagation，BP）算法重复进行了10次电缆寿命评估对照实验。实验共设立了 3个对照组，分别为应用 BP算法、MC-LP算法对带有数据缺失的原始信息进行寿命评估（BP/MC-LP with original data）及应用BP算法对完整信息进行寿命评估（BP with fixed data），并计算了测试集样本的相对老化时间误差百分比的平均值，如图3所示。

由图3可知，3个对照组（BP/MC-LP with original data，BP with fixed data）的平均相对老化时间误差分别在15.300%、2.255%及2.865%左右波动。易知，应用 MC-LP算法对带有数据缺失的原始信息进行寿命评估的评估效果远胜于 BP算法，同时也优于应用BP算法对完整信息进行寿命评估的评估效果。由于实验所采用的 22kV XLPE电力电缆样本的设计使用寿命tT为 30a，因而电缆样本真实寿命的预测误差在0.68a左右，相比 30a的设计寿命而言是可以接受的。

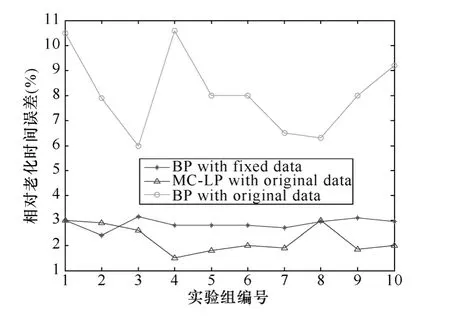
图3 测试集样本的平均相对老化时间误差Fig.3 Test error of average relative aging time

同时，本文考虑了3个对照组（BP/MC-LP with original data，BP with fixed data）的电缆寿命评估实验所得的相对老化时间的方差。3个对照组的10次电缆寿命评估对照实验的相对老化时间方差分别为15.300 0、5.369 3及8.250 8。这表明，在对绝缘状态检测指标有不同缺失情况的样本进行寿命评估的过程中，MC-LP算法能保持较之于BP算法更高的算法稳定性。

此外，本文还讨论了测试集误差与样本数量的关系，以讨论本文所提出的MC-LP算法对不同样本数量的算法稳定性。采用MC-LP with original data及BP with fixed data两个对照组，保持训练集样本与测试集样本的数量比为 3:1不变，增大总样本数量，可得测试集样本的相对老化时间误差百分比的平均值，如图4所示。

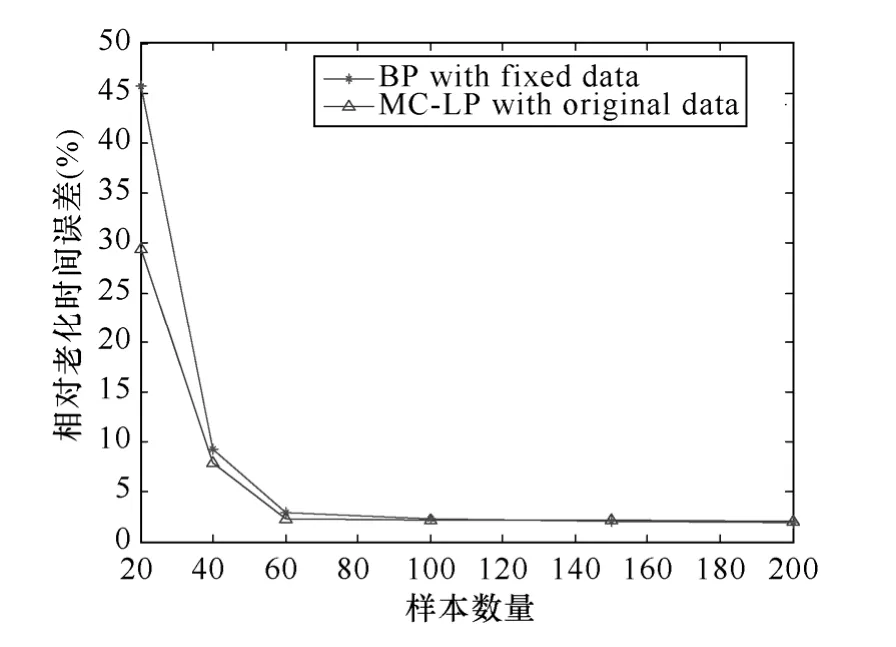
图4 测试集误差与样本数量的关系Fig.4 Relationship between test error and sample number

由图4可知，当样本数量非常小以至于不足以体现电缆绝缘状态检测数据的内在规律时，MC-LP with original data及BP with fixed data两个对照组的实验结果均不理想，且本文提出的MC-LP算法的评估效果明显优于BP算法。而当样本数量充分大时，两个对照组的计算所得误差百分比的平均值逐渐下降并趋于稳定。此时，样本数量对两个对照组的实验结果不再造成显著影响。因而，本文提出的MC-LP算法不仅适用于小样本评估问题，在样本较多时也能保证令人满意的评估效果。

综上所述，本文所提出的MC-LP算法作为一种XLPE电缆寿命的综合评估方法，其电缆寿命的评估结果是精确且稳定的，且评估效果胜于传统的神经网络BP算法。

5 结论

本文所提出的基于低秩矩阵填充的XLPE电力电缆寿命评估方法通过对断裂伸长率、负载伸长率、永久伸长率、DSC出峰温度、击穿实验折算指标及单位长度绝缘电阻等6个绝缘状态检测指标进行相应预处理，保证了其与相对老化时间之间的线性相关性。进而，对带有缺失的电缆信息矩阵进行低秩矩阵填充，实现对目标电缆准确且稳定的寿命评估。实验结果表明，该方法可有效克服样本少、信息缺失等困难，在评估精度上胜于传统的基于神经网络的电缆寿命综合评估方法，为电力电缆寿命评估提供了一种新思路。

[1] 周湶,陈仕军,廖瑞金,等. XLPE电缆电树枝二次生长特性分析[J]. 高电压技术,2009,35(4): 796-801.Zhou Quan,Chen Shijun,Liao Ruijin,et al. Analysis on secondary growth characteristics of electrical trees in XLPE cable[J]. High Voltage Engineering,2009,35(4): 796-801.

[2] 廖瑞金,周天春,刘玲,等. 交联聚乙烯电力电缆电树枝生长的混沌特性分析[J]. 电工技术学报,2012,27(5): 63-69.

Liao Ruijin,Zhou Tianchun,Liu Ling,et al. The chaos characteristics analysis for electrical treeing propagation in XLPE power cables[J]. Transaction of China Electrotechnical Society,2012,27(5): 63-69.

[3] 孙仲民,何正友,戴铭. 基于灰色预测的电力电缆老化过程预警仿真研究[J]. 电力系统保护与控制,2012,40(13): 55-60.

Sun Zhongmin,He Zhengyou,Dai Ming. Simulation study on pre-alarm of power cable aging process based on grey prediction[J]. Power System Protection and Control,2012,40(13): 55-60.

[4] 王志强,周长亮,李文文,等. 船用丁基橡胶绝缘电缆剩余寿命评估[J]. 中国电机工程学报,2012,32(34): 189-195.

Wang Zhiqiang,Zhou Changliang,Li Wenwen,et al.Residual life assessment of butyl rubber insulated cables in shipboard[J]. Proceedings of the Chinese Society for Electrical Engineering,2012,32(34):189-195.

[5] 郭俊豪,吉家稍. 浅析交联聚乙烯材料的热延伸试验[J]. 广东建材,2010,26(6): 135-136.

Guo Junhao,Ji Jiashao. Thermal extension analysis of cross-linked polyethylene material[J]. Guangdong Building Materials,2010,26(6): 135-136.

[6] 姚林朋,徐颖敏,钱勇,等. 基于关联规则的 XLPE电缆局部放电模糊识别研究[J]. 电工技术学报,2012,27(5): 92-98.

Yao Linpeng,Xu Yingmin,Qian Yong,et al. Fuzzy pattern recognition of partial discharge in XLPE cable based on association rule[J]. Transaction of China Electrotechnical Society,2012,27(5): 92-98.

[7] 姚林朋,王辉,钱勇,等. 基于半监督学习的XLPE 电缆局部放电模式识别研究[J]. 电力系统保护与控制,2011,39(14): 40-45.

Yao Linpeng,Wang Hui,Qian Yong,et al. Pattern recognition of partial discharge in XLPE cable based on semi supervised learning[J]. Power System Protection and Control,2011,39(14): 40-45.

[8] 王雅群,尹毅,李旭光,等. 等温松弛电流用于10kV XLPE电缆寿命评估的方法[J]. 电工技术学报,2009,24(9): 33-52.

Wang Yaqun,Yin Yi,Li Xuguang,et al. The method of lifetime evaluation on 10kV XLPE cables by isothermal relaxation current[J]. Transaction of China Electrotechnical Society,2009,24(9): 33-52.

[9] 刘方哲. 基于DSC法电缆热老化寿命的研究[J]. 齐齐哈尔大学学报(自然科学版),2009,25(5): 94.

Liu Fangzhe. Research on the prediction of aging life of cables caused by heat[J]. Journal of Qiqihar University(Natural Science Edition),2009,25(5): 94.

[10] 喻岩珑,李晟,孙辉,等. XLPE电缆绝缘老化与剩余寿命评估的试验方法[J]. 电网与清洁能源,2011,27(4): 26-29.

Yu Yanlong,Li Sheng,Sun Hui,et al. Test method for aging of XLPE cable insulation and remaining life assessment[J]. Advances of Power System and Hydroelectric Engineering,2011,27(4): 26-29.

[11] Lee K W,Mok Y S,Kim B K,et al. Research for remained life of 22kV CV cable system in live-line state[C]. Conference Record of the Twenty-Sixth International Power Modulator Symposium,2004:489-492.

[12] Sun J,Li G,Gao K,et al. Fuzzy comprehensive evaluation for insulation diagnosis of high voltage cable[C]. 2010 International Conference on Power System Technology,Hangzhou,2010: 1-3.

[13] Ranjbar A H,Adnani R,Omranpour H. Application of artificial neural network in cable life time estimation and its failure rate per 100km[C]. IEEE 2nd International Power and Energy Conference,Johor Bahru,2008,22-25.

[14] Cabral R S,Torre F,Costeira J P,et al. Matrix completion for multi-label image classification[C].Advances in Neural Information Processing Systems,2011: 190-198.

[15] Goldberg A,Recht B,Xu Junming,et al. Transduction with matrix completion: three birds with one stone[C]. Advances in Neural Information Processing Systems,2010.

[16] Candès E J,Recht B. Exact matrix completion via convex optimization[J]. Foundations of Computational Mathematics,2009,9(6): 717-772.

[17] Lin Zhouchen,Chen Minming,Ma Y. The augmented lagrange multiplier method for exact recovery of corrupted low-rank matrices[J]. Optimization and Control,1009. 5055,2010.

[18] Wright J,Ganesh A,Ma Y,et al. Robust principal component analysis: Exact recovery of corrupted lowrank matrices via convex optimization[C]. Advances in Neural Information Processing Systems,2009:2080-2088.

[19] 罗涛,陈民铀,曾灿. 电力电缆安全监测中温度场和电场数值关系分析[J]. 电力系统保护与控制,2010,38(5): 20-24.

Luo Tao,Chen Minyou,Zeng Can. Study of numerical relationship between temperature and electric field in power cables safety monitoring[J]. Power System Protection and Control,2010,38(5): 20-24.