基于蚁群算法的电梯群控系统节能策略的优化研究

周卫红，裴 筝，和晓萍，李 晨，陆伟春

(1.云南民族大学数学与计算机科学学院，云南昆明650500;2.郑州大学西亚斯国际学院，河南新郑451150)

电梯群控系统指安装在建筑物内的3台或者3台以上的一组电梯作为一个有机整体，使用一个自动控制系统调度每一台电梯的运行.当前大部分电梯调度算法，如静态或动态分区的最小等待时间、目标层登记算法等，集中在减少乘客的等待与运行时间上，忽略了系统的耗能［1－2］.节能方面［3］，当前的研究集中于单通道优化来减少不必要的能耗，如无传动牵引和能量反馈技术，没有注意减少群控调度的能耗，实际上，在电梯群系统中，单通道节能模型中由于对乘客呼叫不合理的调度降低了节能的效能，因此研究电梯群控节能调度算法是有必要的.

电梯群控是调度一组多台电梯服务于用户的呼叫，属于典型的组合优化问题.我们采用仿生学的优化算法——蚁群算法来解决这个离散组合优化问题，蚁群算法适于解决离散组合优化问题［4－5］，其良好的全局优化能力与快速收敛能力适于电梯群控调度，蚁群算法已经解决了许多调度问题，如TSP，车间调度，无线传感器网络的路由问题［6－8］等.

本文提出一种基于蚁群算法的电梯群调度算法，首先，以建立能耗目标函数作为优化目标，建立一个基于图的搜索机制的蚁群算法控制模型.模型中，每一只蚂蚁代表每一台电梯，每一蚁群代表代表一组电梯，图中的不同结点代表从不同楼层乘客的呼叫服务.每一个结点都会被蚁群遍历，其次，把最少能耗的调度策略问题转化为寻找最短路径动态的TSP问题，模型约束条件来自于结点之间能量分配、电梯运行逻辑、电梯选择概率等，并对算法的收敛性进行了研究，最后的仿真结果表明了调度算法的有效性.

1 能量目标函数

以节能为导向的调度算法目标是尽量减少耗能，首先，以电梯群的能耗为蚁群算法的优化目标函数.电梯群的能耗由2个部分组成:启动与停止耗能;匀速运行的耗能.即E=Ea+Ev，这里，E代表整体的能耗，Ea代表加速与减速的能耗，Ev代表匀速的能耗［9］.

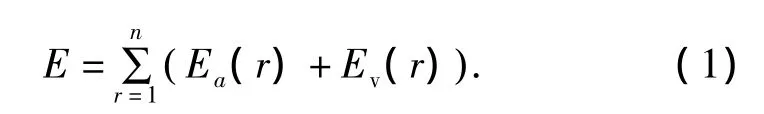
其中n代表电梯群的电梯数量，Ea、Ev是第r台电梯的启停和运行的耗能.Ea、Ev按公式(2)、(3)计算.

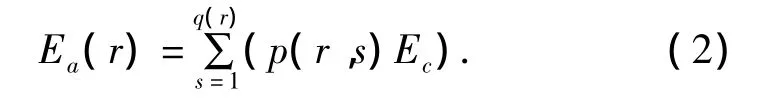
其中p(r，s)表示第r台电梯收到的启停于第s层的请求的数量，q(r)表示第r台电梯响应呼叫的总数，并假设每台电梯启停耗能是个常量Ec.

其中nl(r，s，t)表示第r部电梯响应从t层到s层请求的乘客总人数为乘客的平均质量.h(r，s，t)是该电梯从t层到s层的位移.

综合式(2)、(3)，模型中电梯群控总的能耗目标函数由(4)式计算:

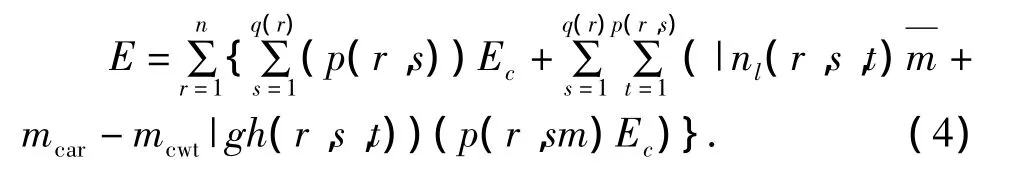
2 蚁群算法调度策略

蚁群算法能有效解决多节点(TSP)问题中的最短路径优化难题，电梯群控调度系统和这些问题很相似，所以非常适合采用蚁群算法来解决.当然这里结点与路径的涵义被延伸并增加了一些特殊的约束条件.

2.1 蚁群算法模型

设n台电梯服务于m层的建筑物，根据调度电梯为各层服务的原则，蚁群模型将服务分为2层，向上服务层和向下服务层，ant1～antn代表n部电梯，u1～up代表向上服务的层，而点d1～dq代表向下服务的层，每一调度方案就是一个拓扑图，蚂蚁访问所有呼叫点，也就是调度群中的电梯服务于每个呼叫层，例如，蚂蚁1→u1→u2→dq，，就是表示蚂蚁 1 按顺序完成向上请求u1，u2，再完成向下请求dq，优化就是从中找出一条最短路径，对比用蚁群算法解决的TSP问题，在这个模型中每条路径的长度的含义已改变了.路径长度被定义为每种调度方案的能耗，因此最短路径代表耗能最少，即最优解.

2.2 约束条件

当用蚁群算法解决电梯群控问题时，有必要讨论模型的约束条件，其主要取决于电梯当前的运行状态与运行逻辑.将所有的呼叫层分为2个部分:上层呼叫与下层呼叫，节点的设置遵循“向上呼叫升序，向下呼叫降序”的原则并依据呼叫交通流的信号采样设置时间间隔.与图1相对应，有u1＜u2＜…＜up，d1＜ d2… ＜ dq.在蚁群优化的过程中，蚁群将按 u1，u2，…，uq、dq，…，d2，d1的顺序设置路径.为简化算法，采用禁忌表避免多部电梯被调到同一呼叫层.

2.3 群控调度优化

2.3.1 信息素更新

τij代表信息素，i代表电梯序列号，j代表呼叫节点的数目.路径ij表示第i台电梯将服务于第j个节点，信息素初始值设置为相同的最小值常量A，设置最小值的目的是为避免在迭代中丢失优化结果，当某些蚁群(电梯群)(ant1～antn)成功找到一条可行性调度方案，每条经过路径的信息素将按(5)式信息素更新.

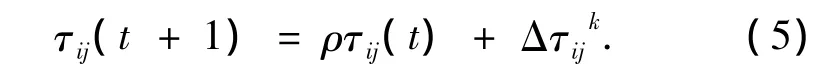
其中C是一个常量，ΓK是第K组电梯群的调度方案总的能耗.

2.3.2 电梯选择概率

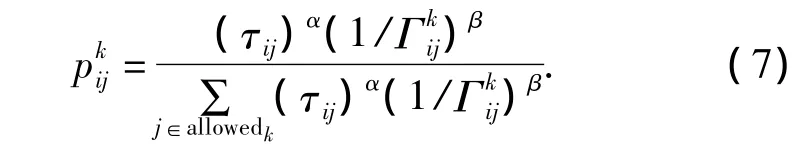
其中allowedk是第k群电梯的可选呼叫节点集是第i台电梯服务于第j层起停呼叫层服务的能耗，α，β是系数.

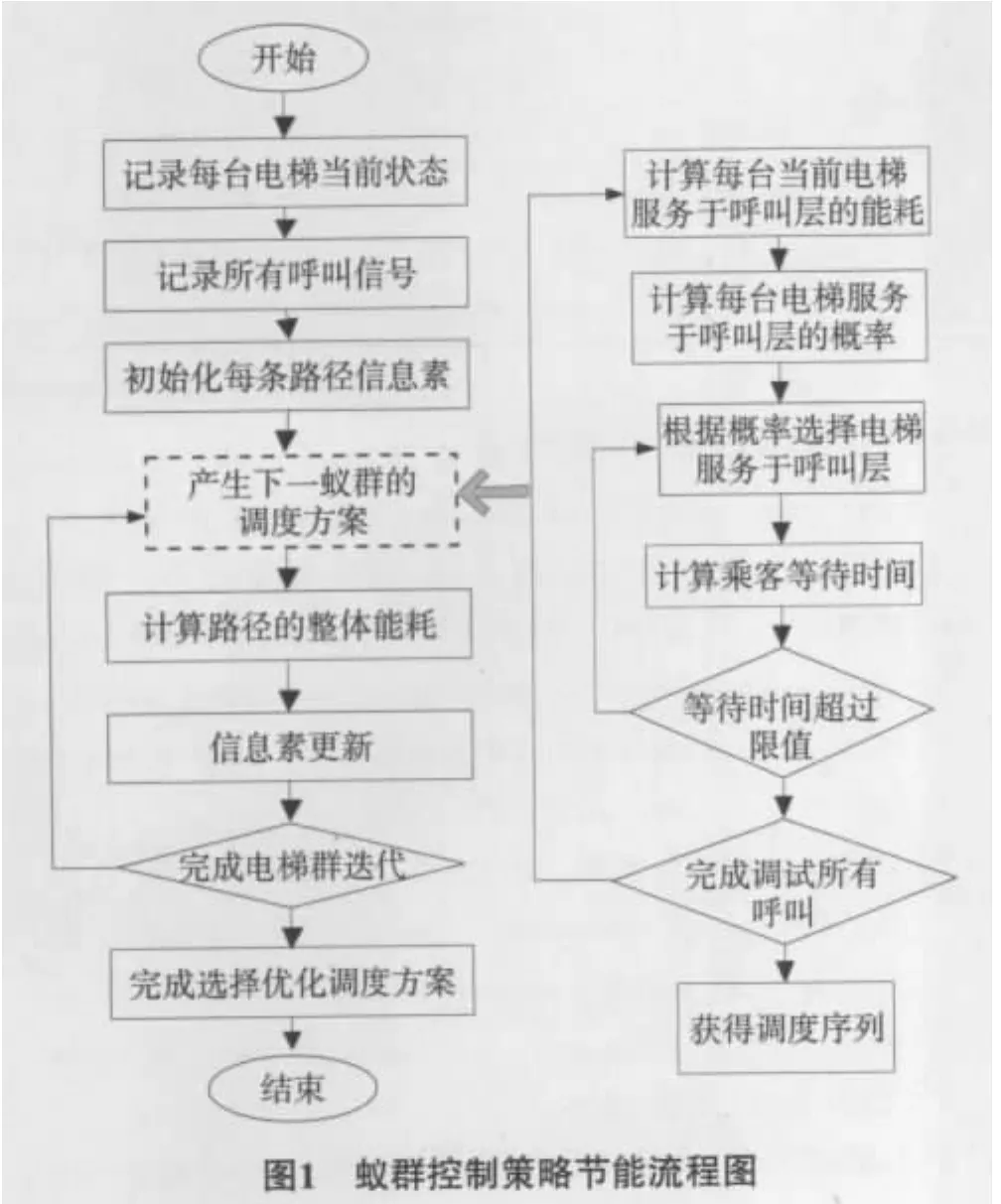
2.4 算法流程图

算法流程如图1所示.

2.5优化机制

蚁群算法是通过迭代寻求优化结果，对于每一组电梯，每一呼叫层由哪台电梯服务的机会是由决定，而由 τij和 1/决定.τij不断更新其值，低能耗可行性路径上的信息素越来越大.而1/确保对每呼叫层响应的电梯最小的能耗，在迭代后，根据蚁群算法的正反馈机制，就能找到优化的低能耗调度方案.图1是蚁群控制策略节能的流程图，在左边的图，算法加载了每个电梯的当前情况和呼叫层、结点集、初始化的信息素，在每次迭代中，将产生一个调度方案，由公式(5)计算总的Γk，更新信息素.每一个调度方案的产生都需要右边的步骤.

在文献［9］的基础上，我们对蚁群模型进行了改进，建立了新的上行高峰流和下行高峰流的更为精细的调度策略，因为上行高峰流中存在乘客逐渐减少而在下行高峰流乘客逐渐增加的规律，本文改进的蚁群算法考虑到这个因素，进行了相关的优化设置.

3 算法的收敛性

蚁群算法的收敛证明［10］如下:

引理 信息素τij有上界τmax=C/(Γmin·ρ).

证明 假设信息素的初始值为τ0，一次迭代后，其最大的增量是c/Γmin，因此最大的信息素是(1－ρ)τ0+c/Γmin，第2次迭代后，信息素的值为(1 －ρ)2τ0+(1 － ρ)τ0+c/Γmin，按此计算，由于信息素的挥发，经过θ次迭代，信息素将会变小或者等于:

因为0 ＜ρ≤1，τmax收敛于 C/(Γmin·ρ).

定理 p*(θ)表示经过θ次迭代至少找到一条优化方案的概率，当给一个足够大的θ，有公式

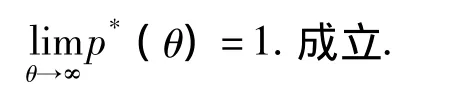
证明 由于信息素是介于τmax和τmin之间，令η=1/，因此η有1个上界和下界.电梯选择概率最小值为

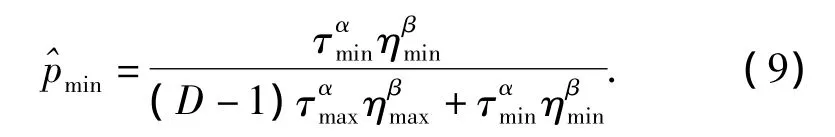
其中D是某一时刻可供选择的呼叫层的数量，任意的调度方案包括最优方案，可以以一定的概率得到，这里n代表呼叫的数量，因此只要一个蚂蚁找到优化方案就得到最优解.对于p*(θ)的下界是由公式(θ)=1－(1－)θ推导得到，只要θ充分大，概率值可能大于1－ε(ε＞0是个任意小的量)，所以有

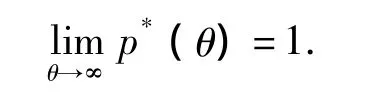
以上的结果表明本文算法能以概率1得到低能耗的调度方案.

4 试验仿真

为了验证算法的有效性，仿真是在虚拟电梯的环境下完成的，表1给出了各参量的数值.能量目标初始参量(由OTIS电梯提供):启停耗能22.5 kJ，箱体800 kg，平衡锤900 kg，乘客平均65 kg.仿真对于3种60 min的上行高峰流，任意间层交通流，下行高峰流交通流，与静态调度算法、最小等待时间调度算法以及文献［9］的算法进行性能比较.本文改进算法中，蚁群算法的参数值是 α=1，β=5，ρ=0.99，迭代次数200，等待时间的极限值为60 s，模拟的结果如表2.

结果表明蚁群算法与其它3种算法相比，在3种交通流的情况下，本文提出的改进蚁群算法能有效地减少能耗，特别是在上行与下行的高峰期.然而在任意层间模式中，效果不明显，另外算法为了追求低能耗牺牲了一些等待时间，例如在高峰期的等待时间有点长，但还是在可接受的范围内，这也是设置阈值的原因，目的是在没有太多时间损耗的情况下尽可能减少能耗.

表1 仿真电梯参量值说明

表2 仿真试验结果

5 结语

采用蚁群算法解决电梯群控制的节能问题，首先建立能量目标函数，其次提出以节能为导向的蚁群算法，建立蚁群电梯模型，提出基于信息素和选择概率函数的收敛优化机制.仿真结果表明，和已有的电梯群控算法相比，基于蚁群的算法在电梯群控中能有效地减少能耗.

［1］TAI J Z，YANG S Y，TAN H.Dispatching approach optimization of elevator group control system with destination floor guidance usingfuzzy neural network［C］//Proceeding of 8th World Congress on Intelligent Control and Automation(WCICA 2008).IEEE，2008:7085－7088.

［2］BARNEY G，SANTOS S D.Elevator traffic analysis，design and control［M］.Stevenage，U.K:Peregrinus，1985.

［3］LEE S，BAHN H.An energy－aware elevator group control system［C］//Proceeding in 3rd IEEE International Conference on Industrial Informatics.IEEE，2005:639 －643.

［4］DORIGO M，CARO G D，GAMBARDELLA L M.Ant algorithms for discrete optimization［J］.Artificial Life，1999，5(2):137 －172.

［5］YAGMAHAN B，YENISEY M M.A multi－objective ant colony system algorithm for flow shop scheduling problem［J］.Expert Systems with Applications，2010，37(2):1361 －1368.

［6］PURIS A，BELLO R，HERRERA F.Analysis of the efficacy of a Two－Stage methodology for ant colony optimization:Case of study with TSP and QAP［J］.Expert Systems with Applications，2010，37(7):5443 －5453.

［7］DHURANDHER S K，MISRA S，OBAIDAT M S，et al.An ant colony optimization approach for reputation and quality－of－service－based security in wireless sensor networks［J］.Security and Communication Networks，2009，2(2):215 －224.

［8］KADONO D，IZUMI T，OSHITA F.An ant colony optimization routing based on robustness for ad hoc networks with GPSs［J］.AD HOC Networks，2010，8(1):63 －76.

［9］ZHANG J L，TANG J，ZONG Q，LI J F.Energy－ saving scheduling strategy for elevator group control system based on ant colony optimization［C］//Proceedings of 2nd IEEE Youth Conference on Information，Computer and Telecommunications.IEEE，2010:37 －40.

［10］STUTZLE T，DORIGO M.A short convergence proof for a class of ant colony optimization algorithm［J］.IEEE Transactions on Evolutionary Computation，2012，6(2):358 －365.