无向图中严格第三短路问题的多项式时间算法
2014-11-14曾庆红
曾庆红
(保山学院数学学院,云南保山678000)
最短路问题是图论中的核心问题之一,最短路算法是许多更深层算法的基础.次短路问题最早是由 Lalgudi和 Papaefthymiou[1]于 1997 年提出,并证明了非负权重有向图中次短路问题是NP-完备的,而当次短路允许含圈时这个问题是有多项式时间算法的.2004 年 Krasikov和 Noble[2]首次设计了一个O(n3m)多项式时间算法解决正权重无向图中次短路问题,这里及下面都要求是简单路,即不含圈和回路.2006年Li等[3]在O(n3m)算法的基础上设计了一个O(n3)多项式时间算法解决正权重无向图中次短路问题.2010年Kao等[4]设计了一个O(n2)多项式时间算法解决正权重无向图中次短路问题.2011年Wu[5]设计了一个O(m+nlog n)多项式时间算法解决正权重无向图中次短路问题.2011年Zhang和Nagamochi[6]设计了一个 O(n6)多项式时间算法解决非负权重无向图中次短路问题.2012年Wu[7]等人提出一个线性时间算法解决非负权重无向图中次短路问题.1971 年 Yen[8]设计一个O(kn(m+nlog n))时间算法解决有向图中第k短路问题.1982年Katoh[9]等人设计一个O(k(m+nlog n))时间算法解决无向图中第k短路问题.而严格第k短路问题目前还没有相关的多项式时间算法解决.
把最短路及次短路算法与最小费用整数流方法结合起来研究严格第三短路问题,并设计一个O(n4)多项式时间算法解决正权重无向图中严格第三短路问题.
1 基本概念与引理
定义1 给定一个无向赋权图G=(V,E;w;s,t),其中s,t是2个固定顶点,w:E→R+是边的长度函数.
1)在 G中寻找一条从 s到 t的路 Pst,使得w(Pst)≤w(Qst),其中:,Qst是从s到t的任意一条路.称路Pst是从s到t的一条最短路.最短路问题是指在图G中求出s-t最短路及其长度.
2)在G中寻找一条从 s到t的路P'st,满足:w(P'st)=min(w(P)|w(P)> w(Pst)),其中:Pst是s到t的一条最短路,P是s到t的任意一条路.称路P'st是从s到t的一条次短路.次短路问题是指在图G中求出s-t次短路的长度.
3)在G中寻找一条从s到t的路P″st,满足:w(P″st)=min(w(P)|w(P) > w(P'st)),其中:P'st是s到t的一条次短路,P是s到t的任意一条路.称路P″st是从s到t的一条严格第三短路.严格第三短路问题是指在图G中求出s-t严格第三短路的长度.
定义2 给定一个无向赋权图G=(V,E;w;s,t),其中s,t是2个固定顶点,是边的长度函数.构造s - t最短路网络 DG=(Vst,Ast;w;s,t),构造方法如下:弧(u,v)∈Ast当且仅当弧(u,v)在原图G中的某一条s-t最短路上,顶点集合Vst是指所有s-t最短路上的顶点组成的集合.称最短路网络上的弧对应与原图G中的边为内部边,其余的边称为外部边.称最短路网络上指向顶点t的弧为正向弧,反之称为反向弧.如果一条s-t路至少含有一条外部边或至少含有一条反向弧,则称这条路中由外部边组成的子路或反向弧组成的子路为反常路.
引理1[4]给定1个无向赋权图G=(V,E;w;s,t),其中 s,t是2 个固定顶点,w:E → R+是边的长度函数.则图G的s-t次短路P'st至少含有1条外部边或至少含有1条反向弧.
引理2[4]给定1个无向赋权图G=(V,E;w;s,t),其中 s,t是2 个固定顶点,w:E → R+是边的长度函数.则图G的s-t次短路P'st上所有的外部边或反向弧一定是连续的.
引理3[2]给定1个无向赋权图G=(V,E;w;s,t,x),其中 s,t,x 是 3 个固定顶点,w:E → R+是边的长度函数.则存在一个O(n2)多项式时间算法求从s经过顶点x到t的最短路Psxt.
引理4 给定1个无向赋权图G=(V,E;w;s,t),其中s,t是2个固定顶点,w:E→R+是边的长度函数.则图G的s-t严格第三短路最多含有2条反常路.
证明 反证法,假设图G的s-t严格第三短路P″st含有 3 条反常路 P1,P2,P3,则存在 1 条只含有 2条反常路(含 P1,P2或 P1,P3或 P2,P3)的 s- t路,路的长度严格大于次短路的长度且严格小于路 P″st的长度,这与 P″st是严格第三短路矛盾.故引理得证.
引理5 给定1个无向赋权图G=(V,E;w;s,t,x,y),其中s,t,x,y是G中4 个固定的顶点,w:E→R+是边的长度函数.则存在一个O(n2)多项式时间算法求从顶点s到顶点x和从顶点y到顶点t的2条点不交的最短路.
证明 首先利用图G构造1个网络N=(V,A;b,c;s,t),构造方法如下:将原图G中的每一条边变成2条向相的弧,每条弧的容量为无穷大,费用为边权重;增加2个顶点u,v,从顶点u加2条弧分别指向顶点x,y,每条弧的容量为无穷大,费用为0.从顶点s,t加2条弧分别指向顶点v,每条弧的容量为无穷大,费用为0.顶点u,v的容量为无穷大,其余顶点的容量为1.要求从顶点s到顶点x和从顶点y到顶点t的2条点不交的最短路就相当于求从顶点u到顶点v的流量值为2的最小费用整数流.所以可以利用最小费用整数流方法在O(n2)时间内求出从顶点s到顶点x和从顶点y到顶点t的2条点不交最短路.
2 算法
求次短路的基本思想:通过分析无向图中最短路问题,利用Dijkstra算法计算2个固定顶点s,t之间的所有最短路,在s-t最短路网络上求次短路.求次短路的方法是对任意顶点x∈V-{t}删除其在最短路网络N上的所有出弧G=(V,E;w;s,t)所对应于原无向图中的边得到一个新的无向图G'=(V,E';w;s,t),然后在新图G'求从起点s经过顶点x到终点t的最短路Psxt,最小者就是次短路.
称次短路算法为:Next-to-shortest path algorithm,简称 NTSPA.详细算法如下[3]:
算法 1[3]NTSPA
输入:无向赋权图 G=(V,E;w;s,t),其中 s,t∈ V,w:E → R+.
输出:求出s到t的次短路或说明无次短路.
Step 1:利用Dijkstra算法求出图G所有s-t最短路,然后构造最短路网络 DG=(Vst,Ast;w;s,t);
Step 2:置S=∅;
Step 3:对于所有x∈V-{t}:
删除顶点x在最短路网络DG中所有的出弧对应于原图G中的边,得到一个新的无向图G'=(V,E';w;s,t);
利用最小费用整数流方法在新图G'=(V,E';w;s,t)中求出从s经过顶点x到t的最短路Psxt;
S=S∪{w(Psxt)};
Step 4:如果(S=∅)则说明没有s-t次短路;否则输出S中的最小者.
定理1[3]算法1可以解决次短路问题,其时间复杂性为O(n3).
下面分析严格第三短路候选路:
1)含1条反常路的s-t路中的第二短路.
求候选路方法:对任意顶点x∈V-{t}删除其在最短路网络N上的所有出弧所对应于原无向图中的边得到一个新的无向图G'=(V,E';w;s,t).利用最小费用整数流的方法在新图G'中求从起点s经过顶点x到终点t的最短路Psxt,这些路的长度一定比最短路更长.其中,最小者就是次短路,而第二小者是严格第三短路的候选路.算法1已经求出这条候选路.
2)含2条反常路的s-t路中的最短路.
求候选路方法:对任意2个顶点x,y∈V-{t},删除顶点x,y在最短路网络DG中的所有出弧所对应于原图 G 中的边,得到新图 G″=(V,E″;w;s,t).利用最小费用整数流方法在新图G″中求出从s经过顶点x,y到t的最短路Psxyt.其中,最小者是严格第三短路的候选路.
定理2 算法1得到的结果S中的最小者是次短路记为:S1,第二小者是严格第三短路的候选路记为:S2.
证明 定理1已经证明了算法1得到的结果S中的最小者是次短路,而S中的第二小者长度一定比次短路更长,所以S2是严格第三短路的候选路.
求严格第三短路的基本思想:首先,求从起点s经过一个固定顶点x∈V-{t}到终点t的最短路,其中最小的是次短路,而第二小者是严格第三短路的候选路之一.其次,求起点s经过2个固定顶点x,y∈V-{t}到终点t的最短路,最小者也是严格第三短路的候选路之一.其中:这2条严格第三短路候选路都是利用最小费用整数流方法来求.最后,比较这两条候选路较小者就是严格第三短路.
先介绍求严格第三短路第2条候选路算法.
称该算法为:Second candidate path algorithm,简称SCPA.详细算法如下.
算法2:SCPA
输入:无向赋权图 G=(V,E;w;s,t),其中 s,t∈ V,w:E → R+.
输出:求出s到t含2条反常路的严格第三短路候选路或说明无含有2条反常路的严格第三短路候选路.
Step 1:利用Dijkstra算法求出图G所有s-t最短路,然后构造最短路网络 DG=(Vst,Ast;w;s,t);
Step 2:置L=∅;
Step 3:对于所有x,y∈V-{t}:
在图G=(V,E;w;s,t)中求出x到y的最短路Pxy;
删除顶点x,y在最短路网络DG中所有的出弧对应于原图G中的边,得到一个新的无向图G″=(V,E″;w;s,t);
利用最小费用整数流方法在新图G″=(V,E″;w;s,t)中求出从s到x和y到t的2条点不交的最短路Psx和Pyt;
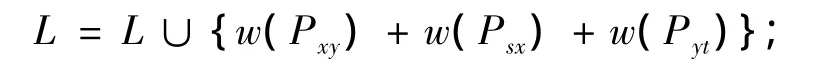
Step 4:如果(L=∅)则,含2条反常路的严格第三短路候选路不存在;否则输出L中的最小者.
定理3 算法2得到的结果L中的最小者L1对应的路一定是简单路.
证明 反证法,假设L中的最小者L1对应的路不是简单路,即含有圈.则路含圈可以分为3种情况:
1)s到x的最短路与x到y的最短路有交点,记距离s最近的交点为x';则用x'替换x可以求得1条含有2条反常路的最短路且w()<w,这与路是最小者矛盾;
2)y到t的最短路与x到y的最短路有交点,记距离t最近的交点为y';则用y'替换y可以求得1条含有2条反常路的最短路且w()<w),这与路是最小者矛盾;
3)s到x的最短路以及y到t的最短路都与x到y的最短路有交点,记距离s最近的交点为x″,距离t最近的交点为y″;则用x″和y″替换x和y可以求得1条含有2条反常路的最短路且w)<w(),这与路是最小者矛盾;
定理3 算法2可以求出严格第三短路的第2条候选路,其时间复杂性为O(n4).
证明 算法2第1步求出从s到t最短路网络DG=(Vst,Ast;w;s,t),显然最短路网络上所有的路都是最短路.对任意2个顶点x,y∈V-{t}For循环,先求出从x到y的最短路Pxy,然后删除顶点x,y在网络DG中所有的出弧对应于原图G中的边,得到一个新的无向图G″=(V,E″;w;s,t),利用最小费用整数流方法在新图G″=(V,E″;w;s,t)中求出从s到x和y到t的2条点不交的最短路Psx和Pyt,最后将三条路合并得到1条从起点s经过2个固定顶点x,y到终点t的最短路,这条路恰好含有2条反常路.所以算法2求得的结果L中的最小者L1是含有2条反常路的严格第三短路候选路.
时间复杂度分析:对任意2个顶点x,y∈V-{t}For语句循环,时间复杂性为O(n2),循环内求x到y的最短路Pxy及用最小费用整数流方法在新图G″=(V,E″;w;s,t)中求出从 s经过2个顶点x,y到t的最短路Psxyt的时间复杂性都是O(n2),故算法2的时间复杂性为O(n4).
最后给出求严格第三短路的算法.
称该算法为:Strictlythirdshortestpath algorithm,简称STSPA.详细算法如下:
算法3 STSPA
输入:无向赋权图 G=(V,E;w;s,t),其中 s,t∈ V,w:E → R+.
输出:求出s到t的严格第三短路或说明无严格第三短路.
Step 1:置T=∅;
Step 2:调用算法1,输出S中的第二小者S2;
Step 3:T=T∪{S2};
Step 4:调用算法2,输出L中的最小者L1;
Step 5:T=T∪{L1};
Step 6:如果(T=∅)则严格第三短路不存在;否则输出T中的较小者.
定理4 算法3可以解决严格第三短路问题,其时间复杂性为O(n4).
证明 算法3将严格第三短路的2条候选路放入集合T,故T中较小者就是严格第三短路的长度.所以算法3可以解决严格第三短路问题.
时间复杂性分析:算法1的时间复杂性为O(n3),算法2的时间复杂性为O(n4).所以算法3的时间复杂性为O(n4).
3 结语
在严格第三短路这个问题的研究中还存在如下2个问题:①本文解决了正权重无向图中严格第三短路问题,但算法的时间复杂性较高.是否能设计出时间复杂性更低的多项式时间算法.②对于非负权重无向图中严格第三短路问题,目前还没有相关的算法.是否能设计一个多项式时间算法来解决该问题.在今后的学习研究中将着力解决这2个的问题.
[1]LALGUDI K N,PAPAEFTHYMIOU M C.Computing strictly - second shortest paths[J].Information processing letters,1997,63(4):177 -181.
[2]KRASIKOV I,NOBLE S D.Finding next-to-shortest paths in a graph[J].Information Processing Letters,2004,92(3):117-119.
[3]LI S,SUN G,CHEN G.Improved algorithm for finding next-to-shortest paths[J].Information Processing Letters,2006,99(5):192 -194.
[4]KAO K H,CHANG J M,WANG Y L,et al.A quadratic algorithm for finding next-to-shortest paths in graphs[J].Algorithmica,2011,61(2):402-418.
[5]WU B Y.A simpler and more efficient algorithm for the next-to-shortest path problem[M]//Combinatorial Optimization and Applications.Berlin Heidelberg:Springer 2010:219-227.
[6]ZHANG C,NAGAMOCHI H.The Next-to-Shortest Path in Undirected Graphs with Nonnegative Weights[C]//CATS.2012:13-20.
[7]WU B Y,GUO J L,WANG Y L.A linear time algorithm for the next-to-shortest path problem on undirected graphs with nonnegative edge lengths[J].arXiv preprint arXiv:1203.5235,2012.
[8]YEN J Y.Finding the k shortest loopless paths in a network[J].Management Science,1971,17(11):712-716.
[9]KATOH N,IBARAKI T,MINE H.An efficient algorithm for k shortest simple paths[J].Networks,1982,12(4):411-427.
