基于极值理论的洪水灾害损失模型研究

何树红，吴 迪，王 珊

(1.云南大学经济学院，云南昆明650091;2.云南大学数学与统计学院，云南昆明650091)

巨灾是指对人民生命财产造成特别巨大的破坏损失，对区域或国家经济社会产生严重影响的灾害事件.按巨灾发生的原因，可将巨灾风险分为自然巨灾风险和人为巨灾风险.自然巨灾是指由自然因素所造成的，通常会影响某一区域和该区域的大量人群.其损失程度不仅取决于巨灾的严重程度，还取决于受灾地区的人口密度、建筑规模和标准、该地区的防灾减损情况等.自然巨灾一般包括地震、冰雹、飓风、洪水、雪灾、旱灾等等.自20世纪80年代以来，全球巨灾的发生频率逐渐上升，频繁的巨灾发生给世界各国造成了巨大的经济损失和人员伤亡，还阻碍了经济的可持续发展和社会的安定.

我国是世界上自然灾害最为严重的国家之一.自20世纪90年代以来，我国因为巨灾造成的直接经济损失呈逐渐上升趋势.据民政部统计资料显示，近10年来，我国每年因自然灾害造成的直接经济损失都在1 000亿元以上，常年受灾人口达2亿多人次.洪水风险是中国自然灾害损失中比较严重的一种.中国现有100多座大城市，有接近半数的人口，5亿多亩耕地和70%的工农业总产值不同程度地受到洪水灾害的威胁.因此，对于洪灾风险损失分布的研究，对我国的抗灾工作，具有十分重大的意义.

洪水巨灾风险往往发生较少，一旦发生则会造成巨大的破坏，这是巨灾风险与一般风险间的差别.由于巨灾风险发生概率极低，一旦发生不仅破坏性巨大而且常伴随次生灾害，从而加大损失程度(如洪水灾害常伴随山体滑坡和泥石流以及瘟疫)，因此洪水巨灾风险的损失分布会呈现出典型的厚尾特征.基于洪水巨灾分布的厚尾性分布特征，需要我们选择恰当的分布函数对其进行拟合.POT模型在拟合具有厚尾性分布的巨灾风险中体现了明显的优势，因此，本文将选择POT模型对洪水巨灾进行拟合.

1 巨灾风险损失模型的基本原理

1.1 广义帕累托分布

帕累托分布也称布拉德福分布，是以意大利经济学家维弗雷多·帕雷托命名的幂次定律的分布.广义帕累托(generalized Pareto distribution，GPD)被定义为:

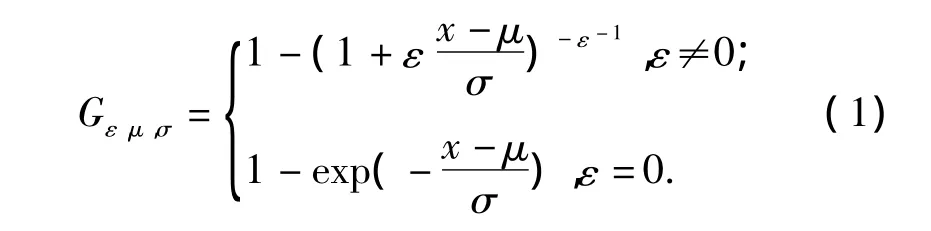
但现实中，以下形式被更为广泛的应用:

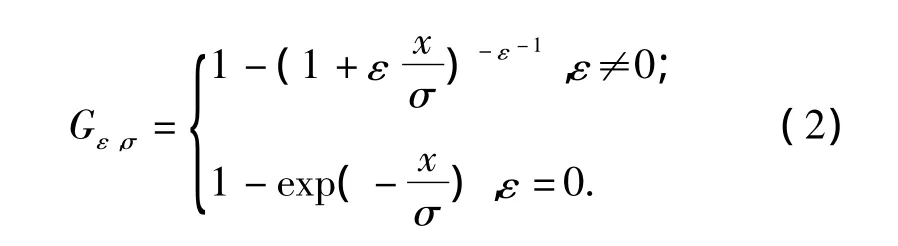
1.2 POT模型

POT模型(peak-over threshold)的建立基于广义帕累托分布，设x1，x2，…，xn为独立同分布随机变量，μ 为门限值，我们称 yi=xi-μ，(i=1，2，3，…，n)为超量损失，超量损失近似服从广义帕累托分布，其分布为:

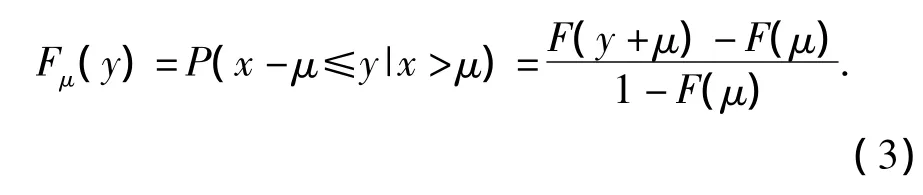
满足POT模型的分布一般为厚尾分布，运用POT模型拟合不需要对整体分布形式做假设，且残缺数据对POT的影响效果并不大，以此模型来拟合厚尾性强的洪水损失分布将会具有较好的效果.

1.3 厚尾性检验

巨灾损失数据一般呈现出较强的厚尾现象，我们有必要对其分布是否真正厚尾作出判断.本文用正态p-p对其厚尾性进行诊断.

正态p-p图是一种散点图，对应于正态分布的p-p图，就是用标准正态分布的分位数为横坐标，样本值为纵坐标的散点图，要利用p-p检验样本数据是否近似于正态分布，只需看p-p图上的点是否近似的在一条直线附近，若样本偏离直线，向下凸，则说明正态分布比该分布增长慢，为厚尾分布.

1.4 帕累托检验

若样本数据具有厚尾性，还需要检验其是否服从帕累托分布，利用帕累托检验纸为检验工具，xi为样本数据，yi为经过标准化后的样本数据，即yi=，若满足帕累托分布的点xi对应点yi的函数图象呈现出一条直线，则样本xi来自帕累托分布总体.

1.5 门限值选取

门限值的选取非常重要，它是估计形状参数ε和尺度参数σ的前提，门限值太高会导致超量损失太少，进而使得尺度参数偏高，门限值太低会导致有偏估计量的产生，达不到拟合效果.

假设样本数据在门限值的左端服从正态分布，且正态分布的均值和方差与GPD分布相同，右端服从广义帕累托分布，其分布函数为:

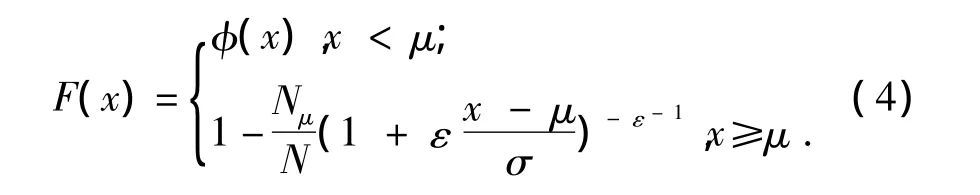
则将样本数据分别代入正态分布与广义帕累托分布的方程中，所得二元方程的解即为所求门限值.

1.6 参数ε和σ的估计

GPD的概率密度函数为:

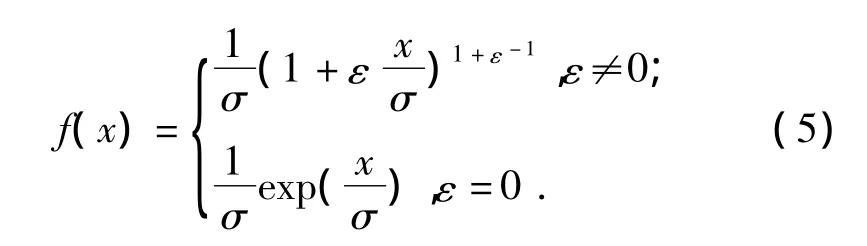
现求解其极大似然函数:

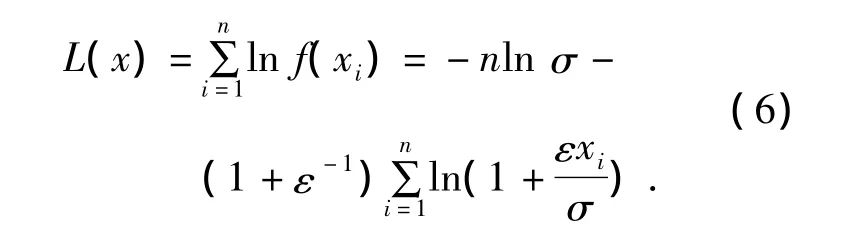
其对数化后的极大似然函数取最大值，得ε，σ为最佳估计量.

若要求得最大函数值，需将极大似然估计函数求偏导，得:

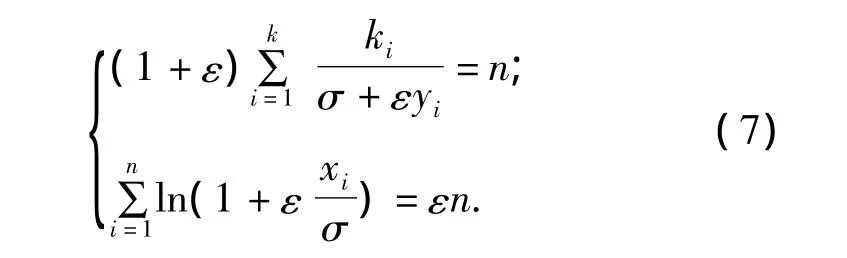
解方程组即可求得ε和σ.

1.7 K－S拟合优度检验

选用K-S拟合优度检验来判断样本数据分布是否与理论分布相一致，若一致，那么结论更具说服力.利用K-S检验法，将原假设设定为H0:F(x)=F0(x)，求出经验分布函数和统计量，其中

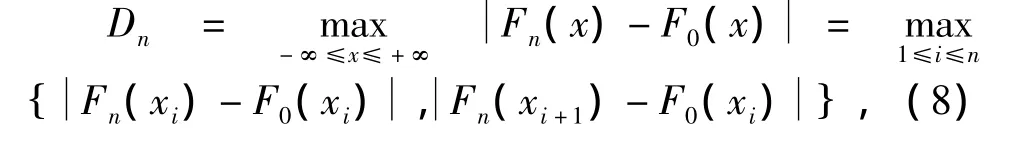
其中规定:Fn(xn+1)=1.

对于给定检验水平α和样本容量n，查Kolmogorov分布的分位数表，得临界值 Dn，1-α，使得 P{Dn≤Dn，1-α};若 Dn≤Dn，1-α，则接受原假设.

2 洪水灾害损失的实证研究

2.1 数据收集与处理

样本数据主要来源于《中国防汛抗旱》登载的从2004年至2012年的每次洪水灾害损失，共225组数据，并以2010年CPI为定基指数，对从2004年至2012年每次洪涝灾害的损失数据进行了调整.

2.2 散点图

为初步观察样本数据的统计分布，现用SPSS软件以时间为横坐标，样本数据为纵坐标做散点图.

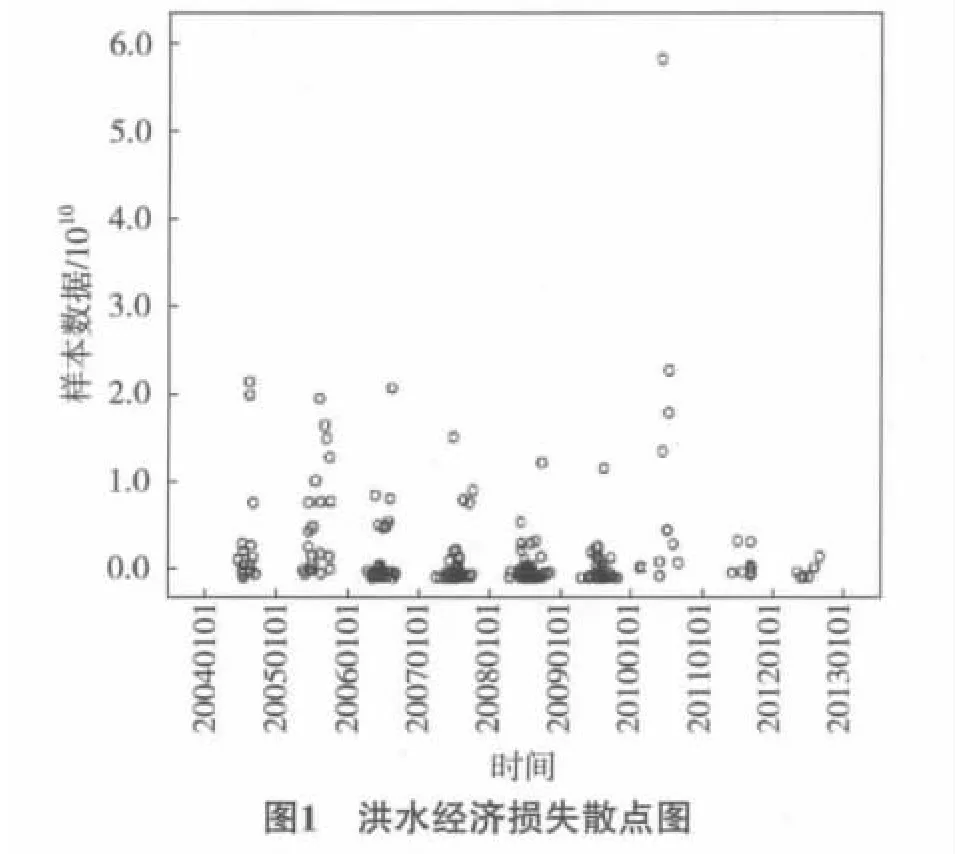
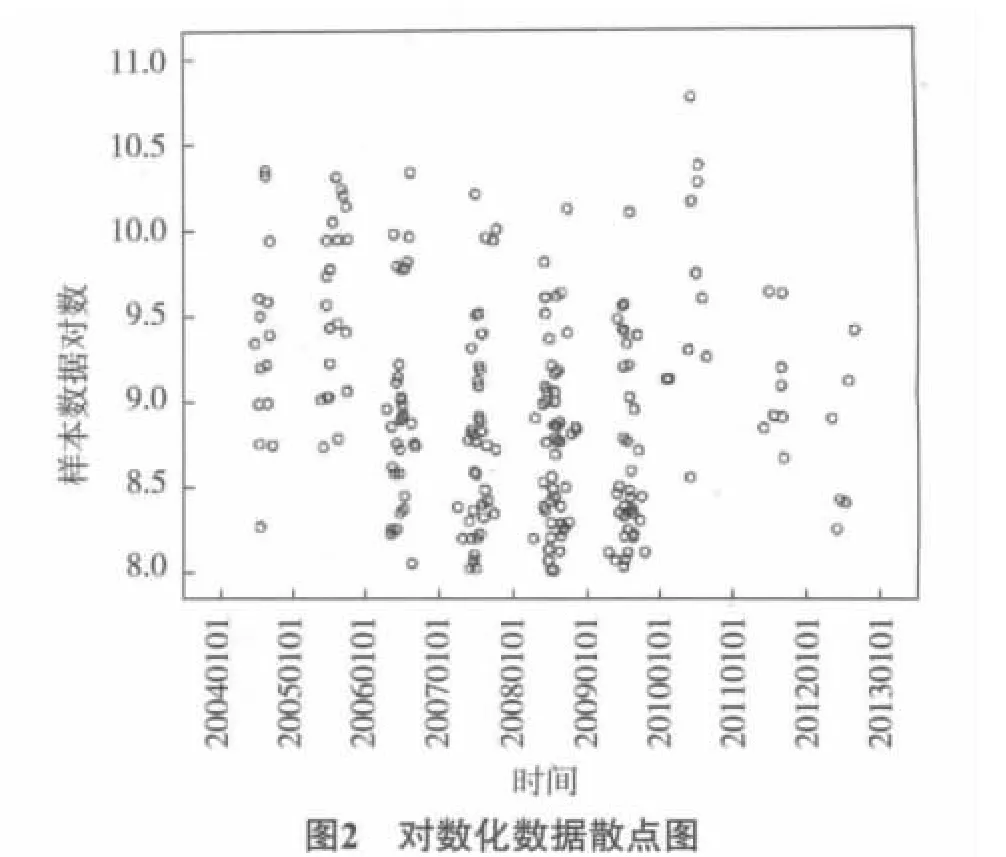
通过发现，点的分布过分密集，无法对其分布进行准确的回归，为克服这一弊端，需将样本数据对数化(图2).

2.3 对数化数据的厚尾性检验

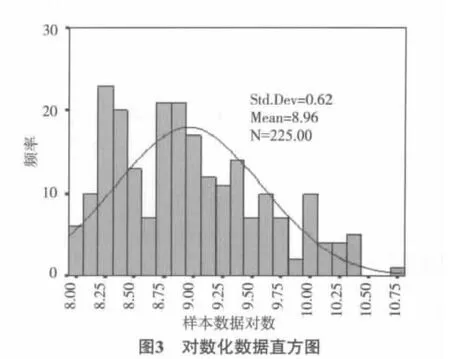
我们通过频率直方图(图3)和正态p-p图(图4)对对数化数据的厚尾性进行检验.检验结果如图5所示.

通过频率直方图3可以看出，与正态分布曲线相对比，对数化数据的尾部分布更为频繁，具有明显的右偏、厚尾、长尾特性，且在正态p-p图4中，对数化数据偏离直线下凸，厚尾特征显著.

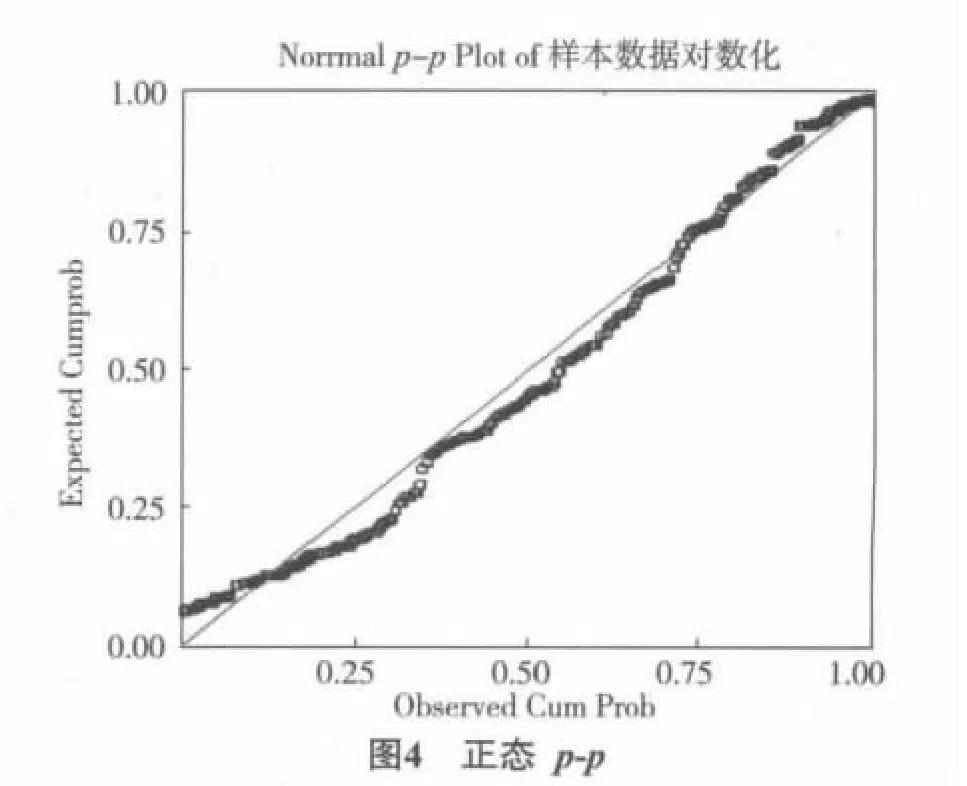
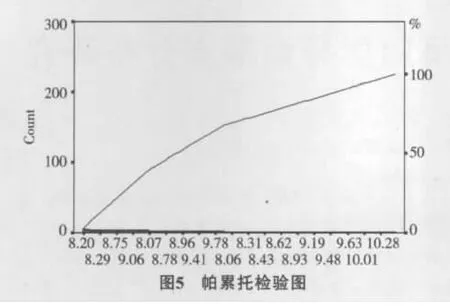
2.4 帕累托检验

将与其标准化后的数据yi相对应，共得到225个点(xi，yi)，将数据代入，画出帕累托检验图(图5)，由图5可见，函数图象近似一条直线，所以对数化数据满足帕累托分布.

2.5 门限值估计

将对数化数据分别代入正态分布与广义帕累托分布的方程中，解二元方程，得μ=8.1.

2.6 ε，σ估计

将 xi，yi，μ 代入公式(7)中，结果见表 1.

表1 分布函数估计

2.7 K－S拟合优度检验

3 结语

本文将基于广义帕累托分布的POT模型用于洪水损失的拟合中，尽管在以往的文献中，Gamma，Weibull和Lognormal等分布被广泛应用，但是在拟合具有强大厚尾特征的巨灾损失分布时，大大降低拟合效果的准确度.POT模型比以往模型具有更好的拟合效果和拟合精度，是一种值得推广的巨灾损失拟合模型，运用该模型进行拟合，对在今后巨灾债券产品进行定价研究具有重要的实际意义.

［1］CHEN S C，FERNG J W，WANG Y T，et al.Assessment of disaster resilience capacity of hillslope communities with high risk for geological hazards［J］.Engineering Geology，2008，98(3):86-101.

［2］KLEINDORFER P R，KUNREUTHER H.The complementary roles of mitigation and insurance in managing catastrophic risks［J］.Risk Analysis，1999，19(4):727-738.

［3］ROOTZÉN H，TAJVIDI N.Extreme value statistics and wind storm losses:a case study［J］.Scandinavian Actuarial Journal，1997(1):70-94.

［4］柳会珍.统计极值理论及其应用研究进展［J］.统计与决策，2006(8):150-153.

［5］徐志勇.极值理论在风险度量与建模中的应用［D］.南京:南京信息工程大学，2006.

［6］解强.极值理论在巨灾损失拟合中的应用［J］.金融发展研究，2008(7):68-71.

［7］王栋，潘少明，吴吉春，等.洪水风险分析的研究进展与展望［J］.自然灾害学报，2006，15(1):103-109.

［8］张琳，孔小玲.洪水风险的可保性分析［J］.上海保险，2008(9):23-27.

［9］卓志，王伟哲.巨灾风险厚尾分布:POT模型及其应用［J］.保险研究，2011(8):13-19.

［10］李海芬.Pareto分布的统计分析［D］.上海:华东师范大学，2004.

［11］欧阳资生，龚曙明.广义帕累托分布模型:风险管理的工具［J］.财经理论与实践，2005，26(137):88-92.