陶瓷材料在滑动接触中的裂纹扩展模拟

胡健锋 廖传伟 李林涛

(三一重工股份有限公司，湖南长沙 410000)

0 引言

裂纹的产生和扩展作为目前很多情况下的主要失效形式，对工程产品的寿命影响巨大，因此研究裂纹的扩展行为对于指导工程产品的加工和制造有着非常重要的意义。而陶瓷材料作为一种新型的工程材料在各个领域应用已经越来越广泛。SIC陶瓷材料的划痕实验是陶瓷材料在滑动接触过程中的裂纹扩展行为的典型实际应用。而裂纹的扩展模拟主要是在有限元软件平台上进行，但在离散元软件PFC2D［1］中也进行过类似的数值模拟。

对于在裂纹扩展的数值模拟中，通常对于断裂准则的选取尤为讲究，断裂准则主要有最大主应力断裂准则、最大主应变断裂准则、延性损伤准则等，而从数值模拟的角度来看，更多的使用的是最大主应力准则，这对于结果更易于控制其精确度。

在有限元模型中其裂纹主要有两种形式，一种是预设了裂纹的扩展路径使之按预定的路径进行节点开裂，另一种是让裂纹根据其设定的判定准则来进行扩展，其中第二种方法就是目前在长裂纹扩展研究中扮演重要角色的扩展有限元方法［2］。

1 扩展有限元(XFEM)及应用

扩展有限元法(Extended Finite Element Method，XFEM)是20世纪末提出的用来求解不连续力学问题的一种数值方法，它能够解决常规有限元法(CFEM)无法解决的一些问题，对于模拟裂纹的随机扩展等不连续问题时特别有效，特别在近几年在不同的应用领域得到了快速发展与应用。XFEM与CFEM的最主要的区别在于它在模拟裂纹扩展的过程中不需要对网格进行重划分而不会导致产生数据奇异。

XFEM方法在目前研究裂纹的扩展中的作用非同小可［2］，文献［3］［4］中采用XFEM方法模拟了摩擦接触裂纹的扩展，其中均采用迭代法求解裂纹面的接触非线性。迭代法的缺点是求解过程复杂，且不能保证收敛到正确解。在此基础上余天堂［5］建立了摩擦接触裂纹问题的XFEM线性互补模型，将裂纹面非线性接触转换为一个线性互补问题求解，不需要迭代求解，且方法具有一定的准确性和有效性。而杨万托［6］采用改进的XFEM对有限板单边裂纹的应力强度因子和I形裂纹的扩展分析，这种方法的优点在于可以直接求出裂纹的表征参数，但局限于I形裂纹扩展，而工程实际中的裂纹扩展绝大部分均为复合型裂纹。董玉文等［7］利用最大环向拉应力开裂准则对基于XFEM的裂纹扩展进行了模拟。Stolarska等把水平集法(LSM)和XFEM结合起来研究裂纹扩展问题，LSM用以表征裂纹和裂尖位置，XFEM用于计算应力和位移，以确定裂纹扩展率［8］。这些方法在不同角度上分析了以XFEM方法为基础的裂纹扩展问题。

2 扩展有限元方法(XFEM)模拟陶瓷裂纹扩展

2．1 裂纹扩展前处理

在前处理建模过程中，裂纹的存在是一种几何不连续性的表现，裂纹的扩展表现为产生新的裂纹面，即几何不连续性的演变。在ABAQUS等有限元软件分析中，一般来讲裂纹可以在三个不同的层次上进行描述:1)整个模型上;2)单元内部;3)节点之间。

而本文则采取的是在单元内部预制裂纹，利用XFEM法来模拟裂纹的扩展。

因为只需要得到平面中裂纹扩展中的参数，因此对于柱面建模的过程中有两种方法，第一种方法是建立和平面一样的变形体，然后在ABAQUS相互作用的模块下将柱面约束成刚体;第二种方法是直接将柱面建模成刚体，本文运用的是第二种方法。

其模型尺寸为500 mm×200 mm，刚体的尺寸为R60的下半圆的2/3，预制裂纹的长度为6 mm，平面的单元类型为CPS4R，在网格的划分中采取的是Structured网格，这样能够划分出比较好的网格。材料的密度为3 210 kg/m3，弹性模量为420 GPa，泊松比为 0．15。

其建模之后的装配体和网格划分如图1所示。

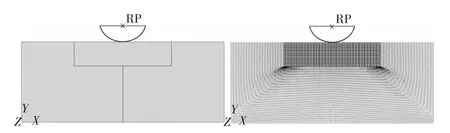
图1 装配体模型和网格划分

2．2 裂纹模拟过程及模拟结果

在模拟裂纹的扩展当中，柱面在平面上面进行滑动使裂纹得以扩展，因为SIC陶瓷材料在滑移的过程中表面残余应力比较小，所以在裂纹扩展的过程中滑过去的部分应力云图显示不明显。其扩展过程及扩展完之后如图2，图3所示。

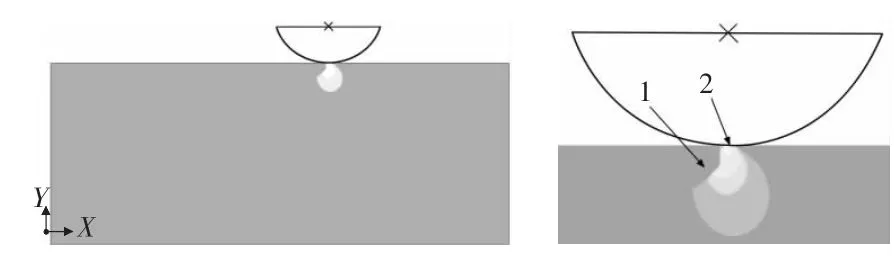
图2 裂纹扩展的过程

图2中数字1、数字2分别代表裂纹及应力区。

裂纹扩展完毕后通过选择裂纹尖端单元可以得出裂纹尖端单元最大剪切应力及最大主应力曲线，如图4，图5所示。

图3 裂纹扩展完成

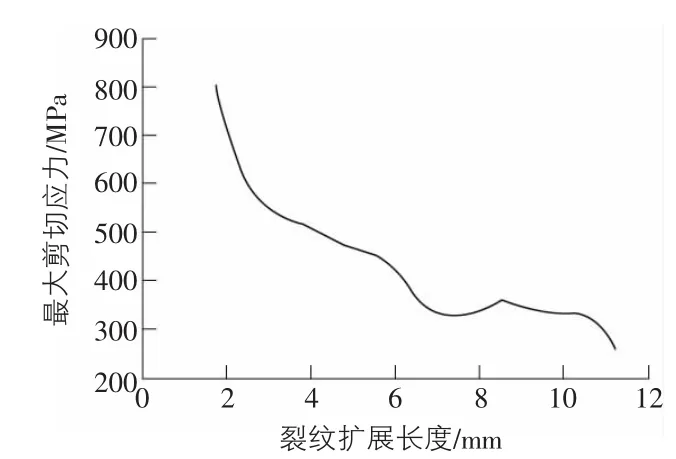
图4 裂纹尖端单元最大剪切应力

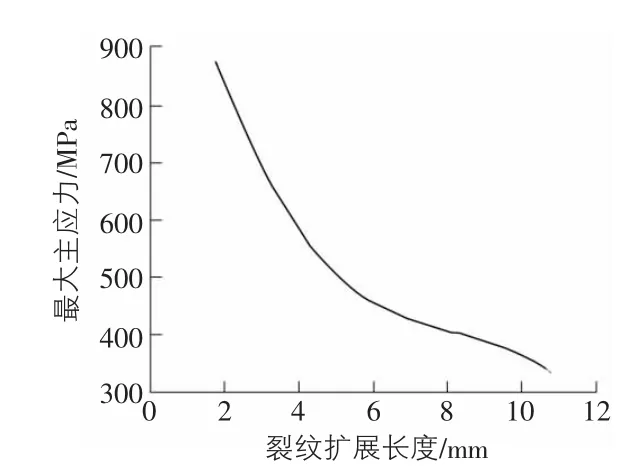
图5 裂纹尖端单元最大主应力

在本模拟中所采取的断裂准则为最大主应力准则，因此其最大主应力可以作为裂纹扩展的重要的参数。在裂纹扩展完的单元中，其最大主应力超过了陶瓷材料所设置的最大主应力，而未扩展到的单元中其最大主应力未达到其设定值，符合断裂准则的判定。

2．3 裂纹扩展路径及裂纹扩展角

SIC陶瓷材料裂纹在有限元软件ABAQUS和离散元软件PFC2D中模拟出来的裂纹扩展路径方向如图6所示，由图6可知裂纹扩展的方向近似，这也在一定程度上证明在ABAQUS中模拟陶瓷裂纹扩展的行为是有效的。

图6 有限元软件和离散元软件模拟出来的裂纹扩展角方向

对于实际裂纹扩展的过程中，裂纹扩展的角度决定了裂纹扩展的轨迹，而在整个裂纹扩展的过程中，在理论上主要利用最大周向拉应力来计算应力强度因子求得扩展角［8］。

在公式中通过对断裂过程中的应力强度因子的求解，可以得出理论解析解与模拟出的对于裂纹的开裂角，分析得到其解析式为:

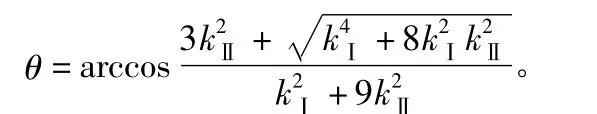
其中，θ为裂纹扩展角;kⅠ，kⅡ分别为第一型和第二型应力强度因子。

而对于陶瓷材料而言 kⅠ=3．5 MPa·m1/2，kⅡ=2．85 MPa·m1/2，将应力强度因子代入上式可以得到裂纹扩展角的解析解θ≈49．7°，得到的裂纹扩展角是在裂纹刚开始扩展的时候的张开方向。

而通过有限元模拟结果及离散元模拟结果测量其裂纹扩展角分别为48°，51°，其误差基本控制在有效范围内。

3 结语

本文对刚性柱面与SIC陶瓷平面的滑动接触过程中的裂纹扩展进行了数值模拟，得出了以下结果:

1)在ABAQUS中运用XFEM法和最大主应力断裂准则来模拟陶瓷材料的裂纹扩展行为，得到其裂纹扩展的过程及应力场的变化规律，并求得其裂纹扩展角;

2)其裂纹扩展角能够与离散元模拟结果及解析解匹配，其误差在允许的范围内，为无损探伤提供了理论的测量视角。

同时本文在模拟方面还存在一定的不足，比如说对于扩展角的求解过程中，因为网格的原因导致了扩展路径只在一定的单元中进行扩展，使得扩展角在后续的测量当中存在着一定的误差，这也是测量解与解析解存在差距的主要原因，同时这也是在裂纹扩展方面进行更深入的研究的一个切入口。

［1］Yang D．Discrete element modeling of the microbond test of fiber reinforced composite［J］．Computational Materials Science，2010(1):16-18．

［2］李录贤，王铁军．扩展有限元法(XFEM)及其应用［J］．力学进展，2005(2):23-25．

［3］Liu Fushen，Borja Ronaldo I．A contact algorithm for frictional crack propagation with the extended finite flementmethod［J］．International Journal for Numerical methods in engineering，2008，76(10):1489-1512．

［4］Khoei A R，NikbakhtM．An enriched finite element lgorithm for numerical computation of contact friction problems［J］．International Journal of Mechanical Sciences，2007，49(2):183-199．

［5］余天堂．摩擦接触裂纹问题的扩展有限元法［J］．工程力学，2010(4):39-40．

［6］杨万托．扩展有限元法在线弹性断裂力学中的应用研究［J］．山西建筑，2006，32(12):36-37．

［7］董玉文，任青文．基于XFEM的混凝土开裂数值模拟研究［J］．重庆交通大学学报(自然科学版)，2009(2):66-67．

［8］张 行．断裂力学［M］．北京:中国宇航出版社，1990．