小型水库大坝稳定分析计算

娄健康 李 慧 张玉辉

(1.华北水利水电大学，河南郑州 450011;2.河南天禹水利工程建设有限责任公司，河南信阳 464000)

1 工程概况

某水库是一座以防洪、灌溉为主，兼顾养殖等综合利用的小(Ⅰ)型水利工程。水库大坝为均质土坝，大坝上游面为干砌块石护坡。水库溢洪道位于大坝右侧，紧邻大坝，为开敞式正堰溢洪道。水库放水设施位于水库右岸，折悬臂表层放水闸，共6孔放水闸门。涵管为人工隧道，进口和出口都为浆砌石结构，无启闭设施。经过方案比选［1］，选择在大坝上游坝坡铺设复合土工膜，并在上游坡脚开挖回填粘土截渗槽，在下游坡脚设棱体排水的除险加固技施。

2 大坝渗流分析

2.1 大坝渗流计算工况

根据SL 274-2005碾压式土石坝设计规范［2，3］规定，渗流分析须对以下水位组合的工况进行复核:1)正常工况:设计洪水位(648.60 m)稳定渗流期;正常水位(647.35 m)稳定渗流期。2)非常工况:水位骤降时(由校核水位降至正常蓄水位)非稳定渗流期;校核洪水位(649.07 m)稳定渗流期。

2.2 大坝允许渗透坡降计算

根据坝体、坝基土体的级配状况，确定坝体、坝基可能的渗透变形类型，再根据坝体、坝基土料的物理性质指标确定其临界水力坡降(Jcr)，依据工程特点及重要性，确定相应的安全系数，求出允许水力坡降(［J］);结合坝体的运行情况，求出下游坝坡出逸点的出逸水力坡降值(J)，最后进行判别。

2.2.1 判别土体变形类型［4］

1)孔隙直径法判别:

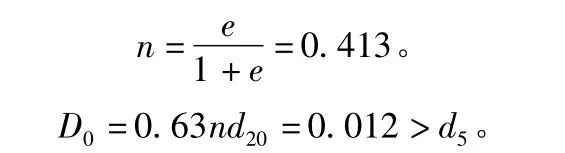
经孔隙直径法判别为管涌型渗透变形。

2)细粒含量法判别:

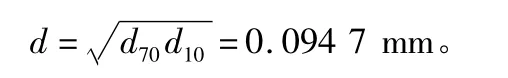
d=0.094 7 mm粒径的细粒含量查级配曲线知P=32%。

经细粒含量法判别为管涌型渗透变形，两种方法判别的结果一致，故该土应属于管涌型土。

2.2.2 计算允许水力坡降

2.3 大坝稳定计算

渗流分析计算断面为大坝主河槽段最大坝高断面，桩号0+136.94处。大坝结构计算断面图见图1。

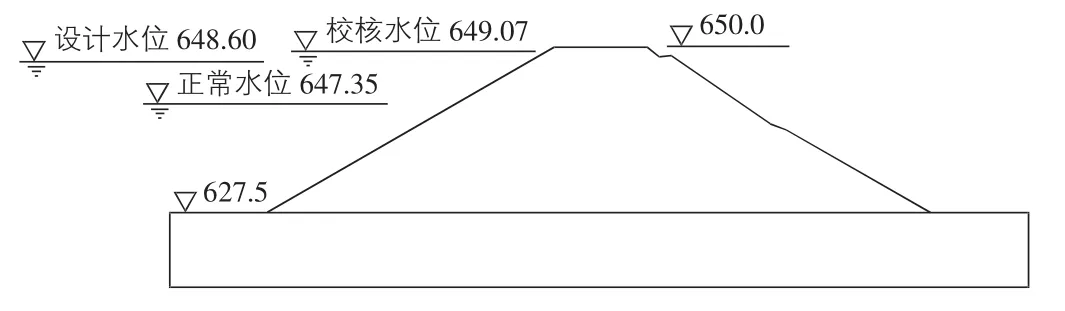
图1 大坝结构计算断面图

将计算断面各重要节点导入理正软件用渗流有限元分析法计算结果如下:正常水位(647.35 m)稳定渗流期正常水位下大坝流网图见图2。

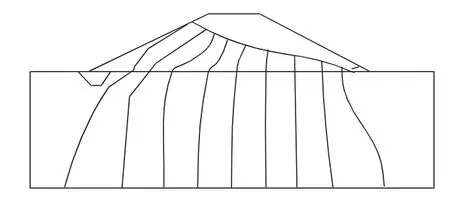
图2 大坝流网图

出逸点高程:627.508 m;单宽渗流量:0.160 97 m/d;坝体出逸点渗透坡降:0.17;坝址附近渗透坡降:0.10;坝基渗透坡降:0.35。

同理对其他工况进行稳定分析，计算所得的水力坡降均小于允许渗流坡降，大坝的浸润线逸出点都在棱体排水内，坝体以及坝基渗流稳定均满足要求。因此，除险加固过后的坝体满足渗流稳定性要求。

3 大坝抗滑稳定分析

3.1 计算工况及参数选取

计算采用北京理正软件，按有效应力计算，计算坝坡抗滑稳定采用不计块间作用力的瑞典圆弧法计算。坝坡抗滑稳定最小允许安全系数在正常运用条件为1.25，非常运用条件一为1.15，非常运用情况条件二为1.10。

稳定分析计算工况分为以下几种:1)正常工况:设计洪水位(648.60 m)稳定渗流时上、下游坝坡稳定分析;正常水位(647.35 m)稳定渗流时上、下游坝坡稳定分析。2)非常工况:水位骤降时(由校核水位降至正常蓄水位)上游坝坡稳定分析。校核洪水位(649.07 m)稳定渗流时下游坝坡稳定分析。3)正常运用遇地震上、下游水位(647.35 m)坝坡稳定分析。

3.2 计算方法

根据SL 274-2001碾压式土石坝设计规范认可的方法不计条块间作用力的瑞典圆弧法。该法［5］假定土坡失稳破坏滑动面为一圆弧面，计算时将可能滑动面以上的土体划分成若干铅直土条，不考虑土条间的相互作用力的影响，据此，可计算出产生滑动的作用力S和抗滑力T。稳定安全系数K定义为抗力相对于圆心的阻滑力矩与作用力产生的滑动力矩的比值:

1)依据B.B.方捷耶夫法确定可能产生的滑动面圆心，即在一扇形区域内。其确定方法如下:从坝坡线AB的中点做一条铅垂线oa和一条与坝坡面成85°夹角的直线ob，然后以o为圆心，分别以R1和R2为半径，做圆弧于oa线交于a，c两点，与ob线交于b，d两点，形成一个环形面积abdc，最危险滑弧面圆心就可能在这个环形面积内。以表1确定环形面积的半径值(H为坝体高度)。

表1 确定环形面积的半径值表

2)费兰纽斯法，在坝坡坡肩A作一条与水平线成β2角的直线，在坡脚B点作一条与坝坡线AB成β1的直线，两直线相交于M1点。然后从坡脚B点垂直向下量取高度H(H为坝高)，并从该点沿水平方向量取4.5H，得 M点，连接 M和 M1点，得直线MM1，并将其延长到M2点。最危险圆弧滑面圆心就在扇形区域内直线附近，如图3所示。

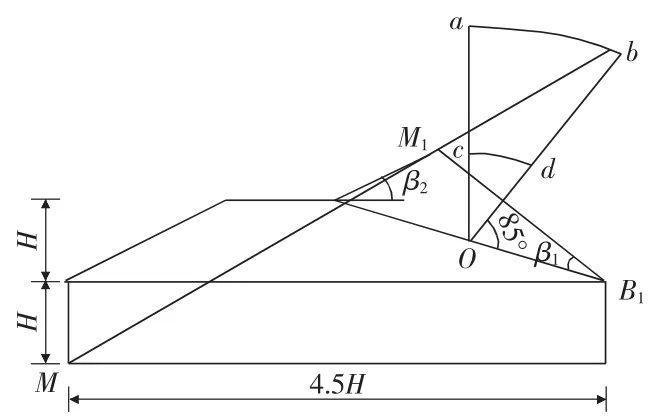
图3 瑞典圆弧原理图

3)采用SL 274-2001碾压式土石坝设计规范规定的瑞典圆弧法计算公式:

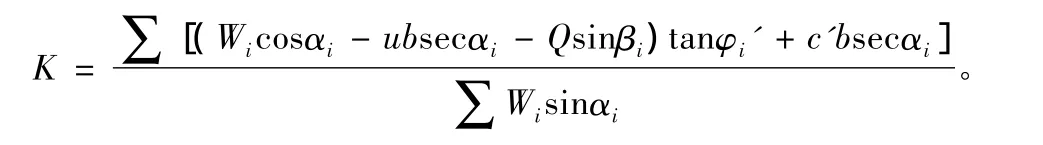
4)计算时可以首先假定滑动圆弧过坝址B1点，在直线MM1上分别选定点1，2，3为圆心画圆弧求解，得出最小K值，假如最小K值圆心在2点，过2点作垂线，再在此垂线上选几个圆心点如4，5点求解K值，假如在5点求得最小K值，圆心5点即为过坝踵B1最危险圆弧滑动面的圆心。计算时将计算出的K值标于圆心之上，连成曲线，从中找出最小的K点。

5)再一次假定滑动圆弧过坝址处B2，B3……按照上面2)的计算方法重复计算B2，B3……的最小安全系数，求出的最小的K值即是最危险滑动面的安全系数Kmin。

3.3 抗滑稳定计算成果

以正常水位(647.35 m)上游坝坡稳定计算为例，计算结果简图如图4所示。

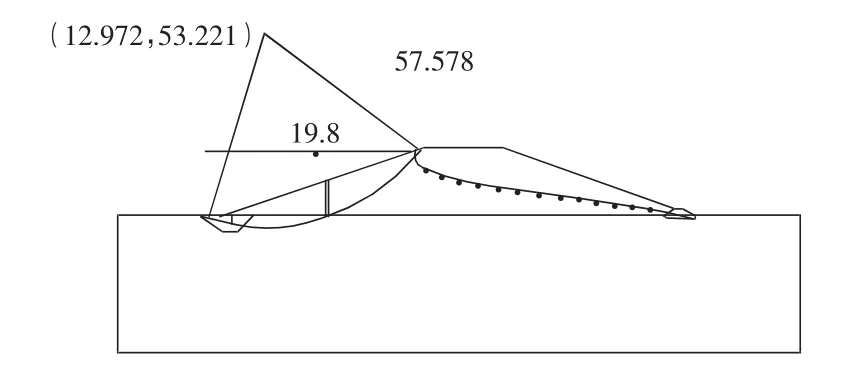
图4 稳定计算结果图

计算得:坝坡抗滑稳定系数最小值为1.644。同理，计算其他工况抗滑稳定系数。计算得各工况的抗滑稳定最小安全系数均满足规范要求。因此，大坝上下游坡在任何情况下均不存在坝坡不稳定的安全隐患问题。

4 结语

在某水库大坝经过水库除险加固技施以后，对其进行渗流及稳定分析计算，结果表明:经水库除险加固技施以后，各工况下浸润线出逸点的渗透比降均小于渗透变形允许水力比降，大坝渗流稳定;大坝上游坝坡在任何工况下抗滑稳定安全系数均小于规范值，下游坝坡在任何工况下抗滑稳定安全系数均大于规范值，大坝抗滑稳定满足规范要求，抗滑稳定安全。

［1］顾慰慈.土石(堤)坝的设计与计算［M］.北京:中国建材工业出版社，2006.

［2］SL 274-2001，碾压式土石坝设计规范［S］.

［3］SL 189-96，小型水利水电工程碾压式土石坝设计导则［S］.

［4］孙明权，樊 静.深覆盖层土石坝渗流性能分析［J］.山西建筑，2012，38(3):234-235.

［5］卢延浩.土力学［M］.第2版.南京:河海大学出版社，2005.

［6］天津大学，林继镛.水工建筑物［M］.第4版.北京:中国水利水电出版社，2006.