基于数值模拟的滑带土蠕变特性研究
2014-11-08李翔,程聪
李 翔,程 聪
(中国地质大学工程学院,湖北 武汉430074)
滑坡是一种重要的地质灾害,给人类的生命财产带来重大威胁。滑带是滑坡最重要的结构,滑坡动态演化规律的三个阶段:蠕动缓滑阶段、等速变形阶段和加速滑动阶段的内因直接与滑带土的蠕变特性有关,而滑带土的长期强度对滑坡的稳定性起着至关重要的控制作用。目前室内岩石三轴蠕变试验主要用于滑坡滑带土的蠕变特性及其长期稳定性研究,通过大量的试验可以揭示滑坡的蠕变力学属性,确定其参数,并建立力学模型[1—5]。但是由于室内岩石蠕变试验费时长、耗资大,在实际操作中比较困难。而数值模拟技术的经济性和快速性,使岩石蠕变试验数值模拟得到了广泛的应用[6—8]。因此,通过实验技术及蠕变理论分析,确定滑带土的蠕变特性,建立其蠕变模型,进而对滑坡演化趋势进行分析,具有重要的理论意义和应用价值。
1 滑带土的室内三轴蠕变试验
本次三轴蠕变试验的滑带土取自位于黄土坡临江Ⅱ号崩滑堆积体上TP4平硐内,滑带土样品的物质组成为粉质黏土夹(含)碎石(角砾),其中黏土矿物以蒙脱石、高岭石、绿泥石、伊利石等亲水矿物为主。为了研究黄土坡滑坡滑带土长期蠕变特性,选择了Burger’s蠕变方程,并对参数进行辨识,同时利用FLAC 3D内置的cvisc模型进行了三轴蠕变试验数值模拟,研究了滑带土的蠕变特性及其长期强度。
1.1 室内三轴蠕变试验
黄土坡滑坡滑带土的三轴蠕变试验在中科院武汉岩土所经过改装的三轴流变仪上进行。轴向加载采用砝码加载,并保持原有的围压系统、反压系统和孔隙水压力系统不变,加载增量一般根据土样的常规力学指标推算出土样达到破坏时的应力值,并确定蠕变试验的加载分级,一般取n=4~8,则每级应力水平的增量为(qf/n),其中qf为在一定的围压σ3下的破坏应力值,加载方法采用陈氏加载法;固结压力一般根据滑带土的埋深来确定,垂向固结压力σ3分别设定为200kPa、300kPa、400kPa。本次三轴固结不排水蠕变试验的稳定标准规定为24h内变形量小于0.01mm,则可进入下一级应力水平试验。
在黏弹性体假设的前提下,利用Boltzmann迭加原理对蠕变试验原始数据进行处理,可以得到各级剪应力作用下的剪应变(ε)随时间(t)变化的蠕变曲线,即分别加载蠕变曲线,详见图1至图3。

图1 围压σ3为200kPa时各级剪应力下滑带土的蠕变曲线Fig.1 Results of creep experiments under differentσ levels with 200kPaσ3
由图1至图3可以看出:当剪应力较小时,剪应变速率逐渐减小,最后趋向于零,试样主要以瞬时变形为主,而没有达到破坏,即发生衰减蠕变;随着剪切力的增加,试样开始出现等速蠕变阶段,最后发生非衰减蠕变,试样发生破坏。
此外,从各蠕变曲线可见,在任何一个剪切荷载作用下,试样都存在着瞬时变形,因此可使用一个弹性元件来模拟该现象。当剪应力较低(小于长期强度)时,随着时间的增加,剪应变速率逐渐降低,近似呈负指数的形式趋于某一渐近线,这种性质可以采用Kelvin体来模拟。将弹性元件和Kelvin体串联起来,可以反映滑带土蠕变变形的瞬时变形和衰减变形阶段。当剪应力大于长期强度时,试样将出现等速蠕变,并最终进入加速蠕变阶段而破坏,因此在上述模型的基础上再串联一个黏性元件就可以模拟滑带土的等速蠕变阶段。这样,模拟瞬时变形的弹性元件和模拟等速蠕变的黏性元件串联,则构成了Maxwell体。

图2 围压σ3为300kPa时各级剪应力下滑带土的蠕变曲线Fig.2 Results of creep experiments under differentσ levels with 300kPaσ3

图3 σ3为400kPa时各级剪应力下滑带土的蠕变曲线Fig.3 Results of creep experiments under differentσ levels with 400kPaσ3
1.2 Burger’s模型及参数辨识
Burger’s模型是由Kelvin体和 Maxwell体串联而成,如图4所示。该模型的蠕变方程为

式中:ε(t)为三轴蠕变试验过程中某级围压σ3及剪应力σ作用下的轴向应变;E1、E2、β1、β2分别为Maxwell和Kelvin单元的弹性模量(kPa)及黏滞系数(kPa·min)。
在剪切蠕变试验中,对于每一个固定剪切荷载值τ,在固定的围压下可将式(1)改写为如下形式:

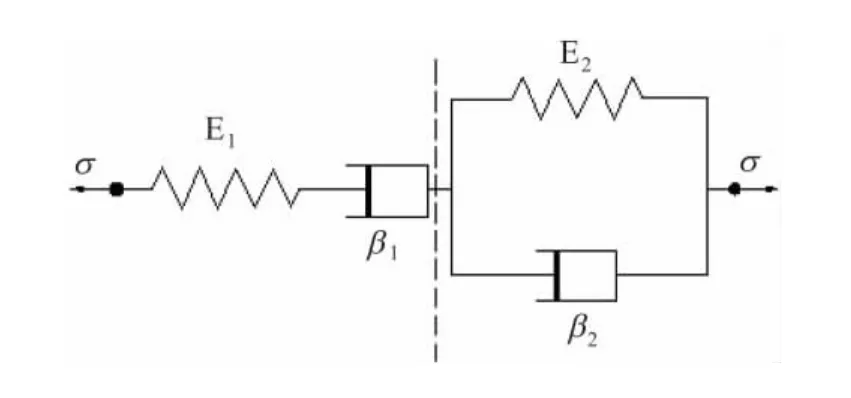
图4 Burger’s模型Fig.4 Burger’s model
式(2)可以进一步简化为

令t=0,式(3)右端等于A,即可以根据瞬时变形来确定A;当时间足够大时,式(3)右端最后一项趋于常数C,则式(3)可看作是直线方程,直线斜率即为B。当土体中的应力小于长期强度时将产生衰减蠕变,此时蠕变过程可能减速进行,蠕变速率逐渐减小,最后趋向于零,变形值也趋向于稳定值。由于衰减蠕变过程中没有等速蠕变阶段,因此式(3)可简化为

将上式中常数项移至等式左边,在等式两边取对数,该式在对数坐标系中也为一直线方程,A已确定,D为直线的斜率,再将D值代入式(4)即可解出C。由此可确定一组初值,然后在 Matlab中利用lsqcurvefit非线性回归工具可回归出A、B、C、D的稳定解,这样Burger’s模型所有的参数均可获得。按上述方法,得到了各固结压力和不同剪切力作用下的Burger’s模型的参数,详见表1。
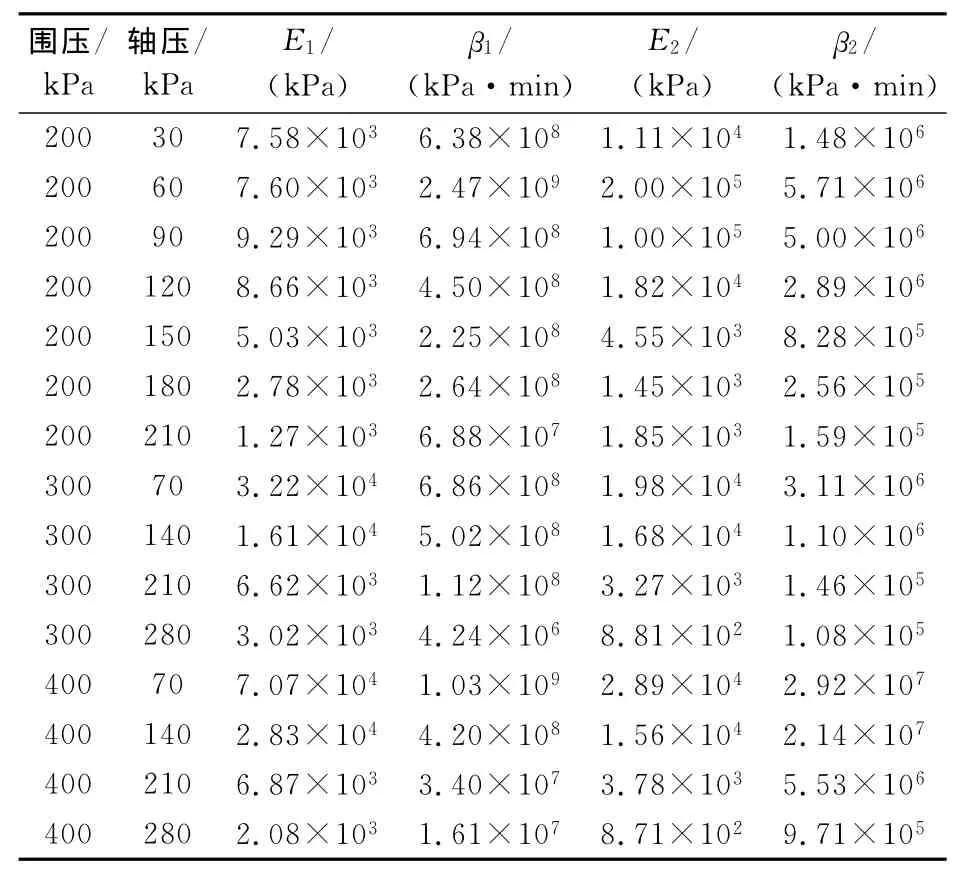
表1 Burger’s模型的参数Table 1 Parameters of Burger’s model
根据蠕变试验数据,本文仅对围压为200kPa时各级剪应力下的蠕变曲线进行分析,Burger's模型的拟合曲线见图5和图6。由图5和图6可以看出:Burger’s模型能较好地拟合出试样在低剪应力情况下的蠕变特性,即试样主要以瞬时变形为主,发生衰减蠕变,随着剪应力的增加,开始出现等速蠕变阶段。

图5 围压为200kPa、剪应力为30kPa时Burger’s模型的拟合曲线Fig.5 Fitting curve of Burger’s model with 200kPaσ3 and 30kPaσ
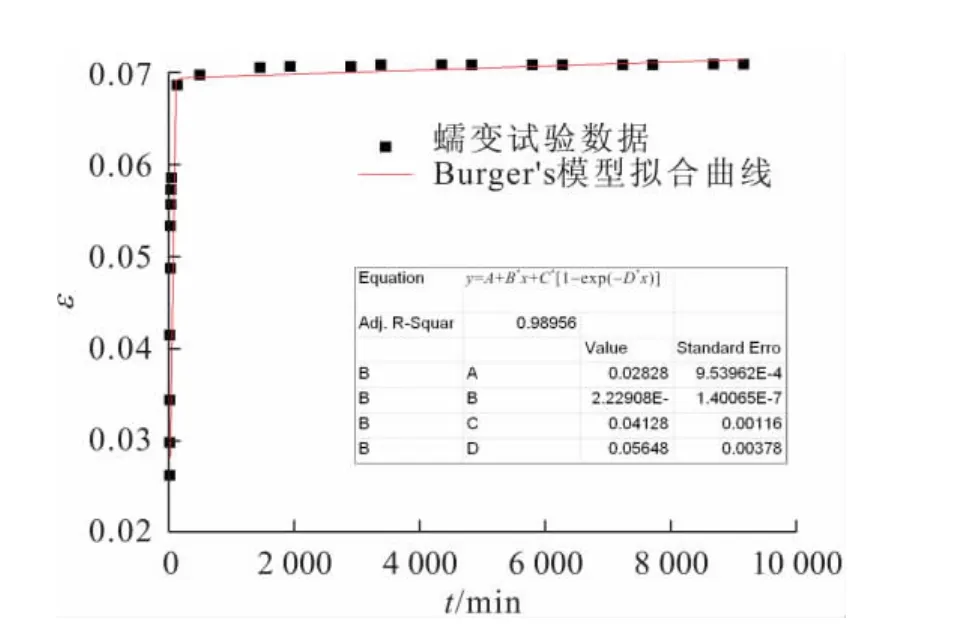
图6 围压为200kPa、剪应力为180kPa时Burger’s模型的拟合曲线Fig.6 Fitting curve of Burger’s model with 200kPaσ3 and 180kPaσ
2 滑带土室内三轴蠕变试验的数值模拟
本文利用Burger's模型拟合参数并借助FLAC 3D对室内三轴蠕变试验进行了数值模拟研究。模型的运行条件与实际的室内试验条件相同,三轴试样尺寸为:d=3.91cm,h=8cm。模型体为圆柱体,网格采取均匀划分,划分的网格为10×10×10,单元底面为竖向位移约束,周围采用应力边界条件;模型顶部荷载为分别加载,荷载为实际室内试验的多级加载值。蠕变模型选用FLAC 3D内置的cvisc模型,即Burger’s(伯格斯)蠕变模型和摩尔-库仑模型合成的伯格斯蠕变粘塑性模型,且采用蠕变大变形模式,根据室内三轴蠕变试验的结果以及室内试验时各级荷载下轴向位移量的大小,对滑带土试样的蠕变参数进行必要的调整后取值,并通过对室内三轴蠕变试验进行数值模拟,可以得出不同围压、不同轴向应力时滑带土分别加载的蠕变模拟曲线,见图7至图9。
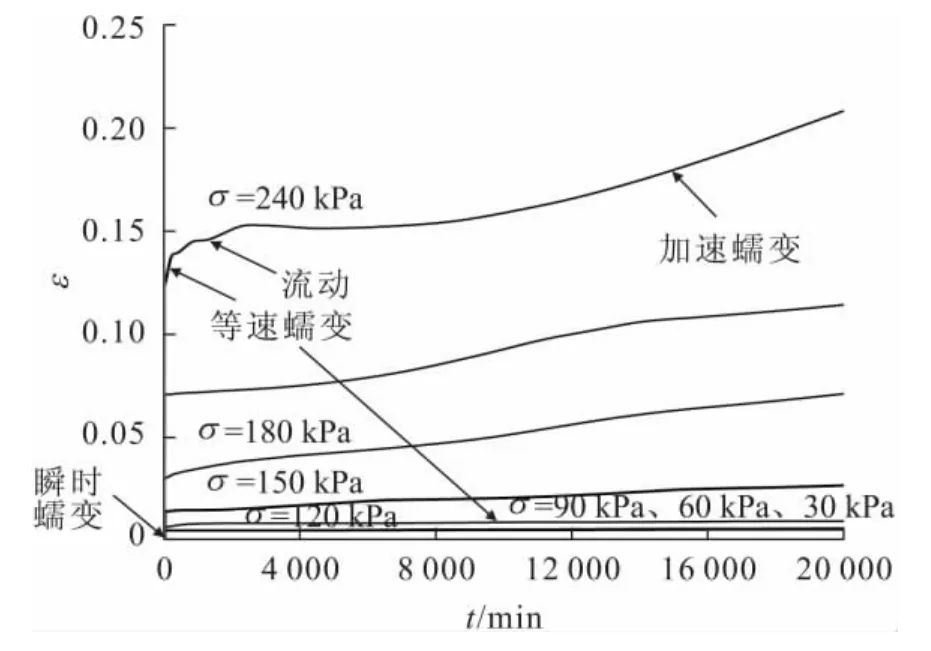
图7 围压σ3为200kPa时滑带土分别加载的蠕变模拟曲线Fig.7 Simulation curves of the creep of the slip soil under different loads with 200kPaσ3

图8 围压σ3为300kPa时滑带土分别加载的蠕变模拟曲线Fig.8 Simulation curves of the creep of the slip soil under different loads with 300kPaσ3
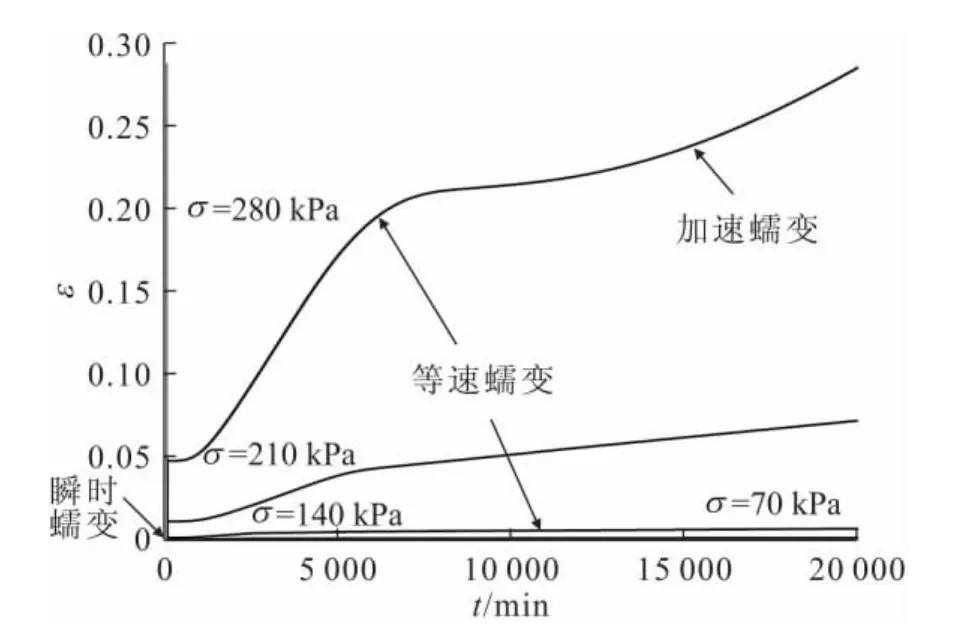
图9 围压σ3为400kPa时滑带土分别加载的蠕变模拟曲线Fig.9 Simulation curves of the creep of the slip soil under different loads with 400kPaσ3
由图7至图9可见,随着围压的增大,滑带土蠕变强度具有明显的提高。较低轴向应力水平下,试件存在明显的瞬时变形,而后产生等速蠕变;较高轴向应力水平下,试件没有明显的瞬时变形,而是一开始即产生等速蠕变,之后岩体的应变速率减小,随着时间的增加,其变形趋于稳定或出现流动,直至试件发生加速蠕变破坏。
3 滑带土的长期强度
土的非衰减蠕变的发展可引起具有加速特征的流动,并最后导致土体破坏,因此土的长期破坏强度可能小于短期荷载作用下的强度值。在实际工程中,一些线性土坡其安全系数达到或甚至超过设计要求,然而在施工完成若干年后,其强度却降低并产生破坏,因此土的长期强度越来越引起人们的重视。在实验室一般采用以下方法来确定土的长期强度:一种方法是将梯级加载的试验结果在对数坐标下绘制应力-应变曲线,找到对数坐标中曲线上有明显拐点的应力作为长期强度极限值τ∞,这是因为在非衰减蠕变阶段变形值急剧增长的结果;另一种方法是根据流动速度来判断,长期强度极限值是区别衰减蠕变和非衰减蠕变的界限值,因此可以通过绘制应力和该应力下的应变速率之间的关系曲线来判断,曲线和应力轴的交点就是长期强度极限值τ∞。
本文采用等时曲线来确定滑带土的长期强度,即为某时刻的应力-应变曲线。首先从数值模拟试验中导出滑带土分别加载蠕变曲线数据,如图10右半部分τ1~τ6等荷载作用下的分别加载蠕变曲线;接着利用Excel,将对应于t4时间的各级应力作用下的时间-应变点A、B、C、D、E投影到图10左半部分,并将横坐标转换成对应的剪应力,然后在新的坐标轴下将投影点连接起来得出其等时曲线。当试验时间足够长时,可以通过t∞直接获取滑带土的长期强度;当试验时间较短时,也可以通过不同时刻的应力-应变曲线的拐点连线来确定长期强度。图11至图13为不同围压、不同时刻滑带土的轴向应力-轴向应变关系曲线,即等时曲线。
由图11至图13可以看出:不同轴向应力下的等时曲线由近似线性段和非线性段组成,并且有转折点,将各个转折点连接起来,并利用指数函数进行拟合,在轴向应变达到0.15时可以认为该试样在不同围压下的长期强度。采用这种方法可以得出:围压为200kPa下滑带土的长期强度为130kPa,围压为300kPa下滑带土的长期强度为180kPa,围压为400kPa下滑带土的长期强度为200kPa。通过绘制莫尔应力圆可以得到滑带土的长期强度参数:内聚力c∞为21.20kPa,内摩擦角φ∞为18.56°。
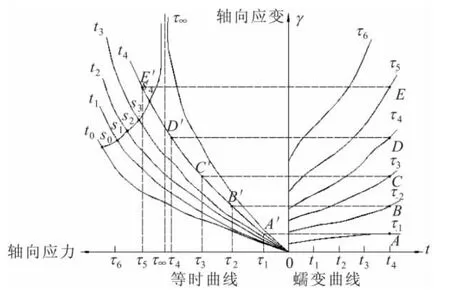
图10 滑带土的等时曲线图解法示意图Fig.10 Sketch map of isochronal curve graphical method

图11 围压σ3为200kPa时滑带土的等时曲线Fig.11 Isochronal curves of the slip soil with 200kPaσ3

图12 围压σ3为300kPa时滑带土的等时曲线Fig.12 Isochronal curves of the slip soil with 300kPaσ3
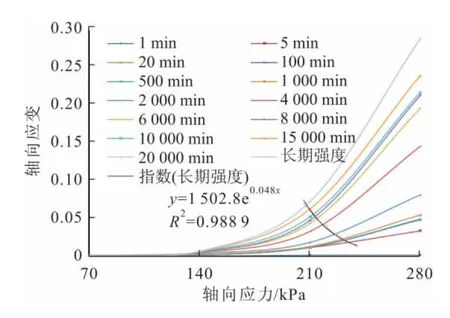
图13 围压σ3为400kPa时滑带土的等时曲线Fig.13 Isochronal curves of the slip soil with 400kPaσ3
4 结 论
(1)本文以室内三轴蠕变试验结果为依据,通过对Burger's蠕变方程中各参数进行辨识,从而为描述黄土坡滑坡滑带土的力学特性,特别是其长期蠕变特征打下了一定的基础。
(2)数值模拟试验结果与室内三轴蠕变试验结果具有很好的相似性。数值模拟试验主要依托三轴蠕变试验结果,在满足其误差的基础上,利用数值模拟,试验结果可以获取滑带土分别加载下的等时曲线,从而得到滑带土的长期强度参数:内聚力c∞为21.20kPa,内摩擦角φ∞为18.56°。
[1]汪斌,朱杰兵,唐辉明,等.黄土坡滑坡滑带土的蠕变特性研究[J].长江科学院院报,2008,25(1):49-52.
[2]严绍军,项伟,唐辉明.大岩淌滑坡滑带土蠕变性质研究[J].岩土力学,2008,29(1):58-63.
[3]邹良超,王世梅.古树包滑坡滑带土蠕变经验模型[J].工程地质学报,2011,19(1):59-64.
[4]曹运江,黄润秋.某水电站高边坡煤系软弱结构面流变特性试验研究[J].岩石力学与工程学报,2008,27(增2):3732-3740.
[5]王琛,唐明.三峡泄滩滑坡滑动带土的Singh-Mitchell蠕变方程[J].四川大学学报(工程科学版),2003,35(5):93-95.
[6]王旭东,付小敏.压缩蠕变力学试验的数值模拟研究[J].工程地质学报,2009,17(4):533-537.
[7]郑俊.某滑坡滑带土流变模型构建及FLAC3D二次开发[D].宜昌:三峡大学,2009.
[8]陈育民,刘汉龙,邓肯·张.本构模型在FLAC3D中的开发与实现[J].岩土力学,2007,28(10):2123-2126.
[9]Itasca Consulting Group.FastLagrangianAnalysisofContinua in3Dimensions[M].MN.USA:Itasca Consulting Group Inc.,Minneapolis,2002.
[10]周德培等.流变力学原理及其在岩土工程中的应用[M].成都:西南交通大学出版社,1995.
