莱钢锯机万向接轴故障分析

2014-11-06李雪涛

冶金设备 2014年1期

关键词：动轴主动轴万向节

李雪涛

（山钢集团莱钢设备检修中心山东莱芜 271104）

1 前言

锯机作为冶金轧材生产线的主题设备，其稳定的工作状态至关重要，但在实际生产过程中，经常出现锯机震动过大造成轧件切斜、传动接轴十字包断裂等事故，影响生产的稳定运行，因此依据原设计，结合现场实际，对接轴设计进行适应性改造。

2 锯机万向接轴故障分析

莱钢轧材生产线主要使用型号为SWP250的进口万象接轴，作为锯机设备的传动部件。万向接轴在生产中的常见故障主要是运行中出现动平衡破坏，震动过大，轧件切斜，万向节十字轴处出现裂纹或断裂等现象，这些问题是万向节传动形式当中典型的疲劳破损现象引起的。

图1 十字轴总成结构图

3 锯机万向接轴受力分析

锯机万向接轴采用十字轴式刚性万向节传动形式。从动十字轴旋转的角度是不均匀的。其运动学特点简单分析如下（如图2所示）。

设主动十字轴与从动十字轴夹角为α，主动十字轴以等角速度ω1旋转，十字轴万向节转动半径为r。先看两个特殊位置的速度：

1）主动十字在垂直位置，并且十字轴平面与主动轴垂直，如图2 a）所示。主动叉与十字轴连接点a的线速度Va在十字轴平面内，Va＝ω1r；从动叉与十字轴连接点b的线速度Vb在与主动叉平行的平面内，并且垂直于从动轴，点b的线速度Vb可分解为在十字轴平面内的速度V＇b和垂直于十字轴平面的速度Vb″。由速度直角三角形可看出在数值上Vb＞V＇b。十字轴是对称的，oa＝ob。当万向节传动时，十字轴是绕O点转动的，其上a、b两点于十字轴平面内的线速度在数值上应相等，即V＇b＝Va，因此Vb＞Va。因此可知，当主从动叉转到所述位置时，从动轴的转速大于主动轴的转速。

图2 万向节运动学图示

2）主动叉在水平位置，并且十字轴平面与从动轴垂直，如图2b）所示。此时主动叉与十字轴连接点a的线速度在平行于从动叉的平面内，并且垂直于主动轴。线速度Va可分解为在十字轴平面内的速度V＇a和垂直于十字轴平面的速度Va″，根据同样道理，在数值上，Va＞V＇a，而V＇a＝Vb，因此，Va＝Vb即当主从动叉转到所述位置时，从动轴转速小于主动轴转速。

3）显然，由a点，Va＝ω1r，V＇b＝Vbcosα＝ω2rcosα，可知

ω1＝ω2cosα或ω2＝ω1／cosα

由（2）点，V＇a＝Vacosα＝ω1rcosα，Vb＝ω2r，可知

ω1＝ω2／cosα或ω2＝ω1cosα

即当主动十字轴以等速度ω1转动，主动叉由垂直位置转到水平位置时，从动十字轴的角速度由大于主动十字轴角速度的最大值ω1／cosα变化至小于主动叉角速度的最小值ω1cosα。主动轴再转90°，从动轴的角速度又由最小值变至最大值。从动轴角速度的变化周期为180°。即在一圈内变化两次，而且从动轴不等速的程度是随两轴间夹角α的加大而加大。

4）刚性十字轴式万向节从动轴以每周变化两次的周期进行不等角速度旋转，其旋转的角加速度会引起较大的惯性力矩，从而可能引起传动系统的扭转振动，刚性十字轴式万向节传动中主动十字轴扭矩M1与从动十字轴扭矩M2的变化关系即动力学特征。简要说明如下：

5）如果不计万向节里的摩擦损失，即有M1ω1＝M2ω2由万向节运动学特征可知，当ω1以等速旋转时，随万向节旋转所处位置不同，从动轴角速度ω2在ω1／cosα至ω1cosα之间不均匀变化。显然，当万向节主动叉处在垂直位置，万向节十字轴平面与主动轴垂直时，如3a）图所示，从动叉轴上的扭矩最小，即M2min＝M1cosα。当万向节主动叉在水平位置，万向节十字轴平面与从动叉轴垂直时，从动叉轴上的扭矩最大，即M2max＝M1／cosα。

6）主动叉对十字轴的作用力矩，除主动扭矩M1之外，还有作用在主动叉平面的弯曲力矩M＇1。同理，从动叉对十字轴也作用有从动轴反扭矩M2和作用在从动叉平面的弯曲矩M＇2。

如图3a）所示，由于M1作用在十字轴平面，M＇1必为零，因M2的作用平面与十字轴不共平面，必有M＇2存在。向量M＇2是垂直于M2的，合向量M＇2＋M2指向十字轴平面的法线方向，而与M1方向相反，大小相等。由力矩向量三角形可知M＇1＝M1sinα。当万向节主动叉处于水平位置，十字轴平面与从动轴垂直时，同理可知M＇2＝0主动叉上的附加弯曲力矩M＇＝M1tgα，如图3b）所示。

由此可见，附加弯曲力矩的数值零与以上两公式所表示的最大值之间变化的，其变化周期为180°。即每转变化两次。附加弯矩可在万向节主、从动轴支承上引起周期性变化的径向载荷，并有可能激起支承的振动。

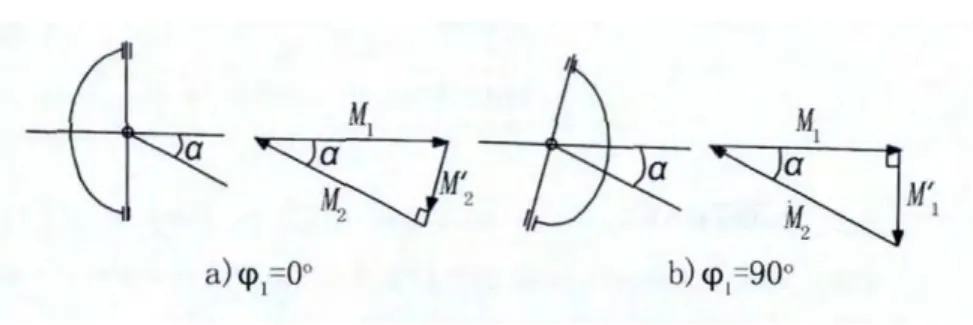
图3 十字轴万向节的力矩平衡

7）万向接轴在某个工作角度下，在十字轴对称轴的平面内将产生二次力偶。二次力偶产生在十字轴的轴心交点，形成力偶矩使十字轴弯曲，使滚针轴承和十字轴受到附加的二次载荷。根据图4、图5进行受力分析

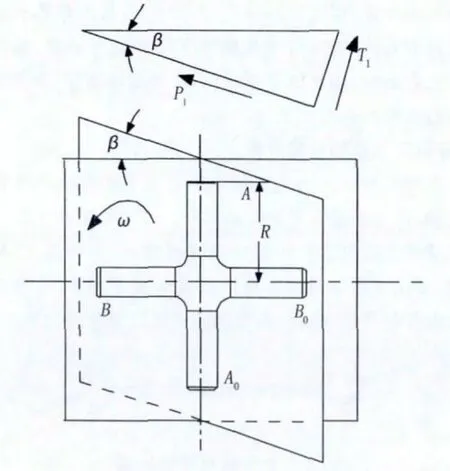
图4 驱动轴AAO受力分析

驱动轴AA0受力分析：

作用于十字轴A A0上的力P1、T1：

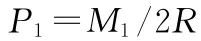
式中M1—驱动轴力矩；

P1—作用于十字轴上的力；

R—力的作用半径。

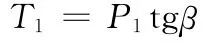
式中T1—作用于驱动轴轴承座上的二次载荷；

β—倾角。

二次载荷T1形成的力偶矩为：

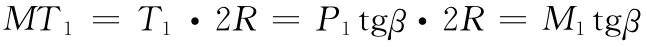
当被动轴B B0位于轴承座的旋转轨迹交线时，受力分析如图5。

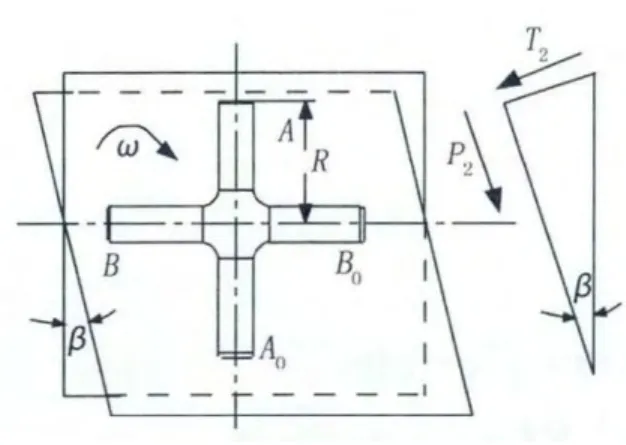
图5 BB0驱动轴受力分析

同理可计算出作用在十字轴BB0上的二次载荷T2：

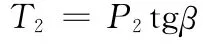
又因

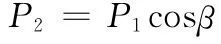
二次载荷T2及形成的力偶矩为：

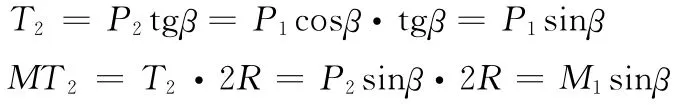
式中M2—从动轴力矩；

P2—作用于十字轴上的力；

R—力的作用半径。

根据计算结果分析，接轴每旋转90°，驱动轴和从动轴的二次载荷力矩从零到最大，当十字轴的中心线与轨迹交线相重合时达到最大值。此外，每当转过180°时，作用在十字轴上的力改变方向。

4 万向接轴的受力计算

图6为万向接轴力学模型简图。

图6 万向接轴力学模型简图

根据瞬时功率相等的原则，从动轴上的转矩为

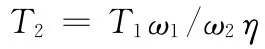
当φ1＝90°或270°时从动轴上的转矩达到最大值

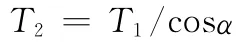
当φ1＝0°或180°时从动轴上的转矩达到最小值

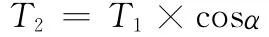
当轴间角α不等于零时，由于主从动轴的回转平面不在同一平面，因而产生附加转矩，其值与主动轴转角和轴间角的大小有关，即当φ1＝90°或270°时，作用在主动轴叉上的附加弯矩达到最大值。

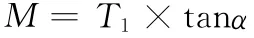
式中φ1—主动轴和中轴的转角；

α—主动轴与中轴的轴间角；

ω1、ω2—主动、从动轴的角速度。

由于传动轴转速波动引起的附加惯性转矩可按经验公式将计算出的最大转矩乘以系数1.1。

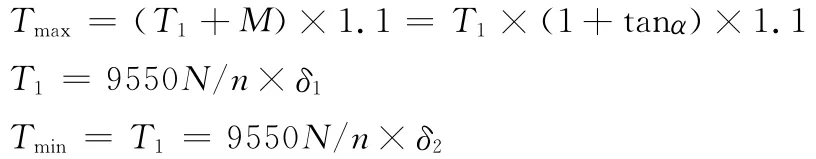
式中δ—电机输出系数。

计算结果为

同时对锯机驱动电机的工作电流进行随机抽查，通过电机工作电流对照电机的电流、功率曲线推算矫锯机电机输出转矩，见表1。

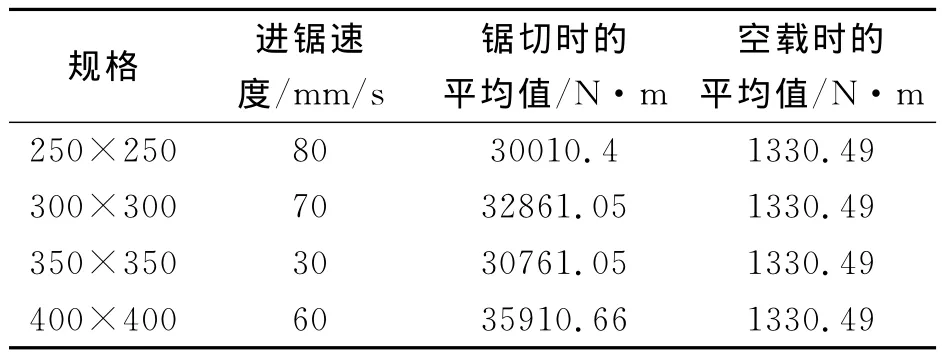
表1 驱动电机技术参数

通过表1对照，计算结果与实际输出转矩基本相符，证明计算结果是正确的。

5 万向接轴的校核

锯机万向接轴在锯切时受交变载荷，在强度校核中取万向接轴疲劳转矩23000N·m。通过对照现场万向接轴输入转矩计算值，万向接轴在锯切时的转矩最大值远大于万向接轴疲劳转矩小于万向接轴的额定转矩。当工作转矩大于万向接轴的疲劳转矩时，万向接轴就会发生疲劳损坏，但不会立即表现出来，只有疲劳损坏累积到一定程度，万向接轴才会发生断裂。因此将矫直机万向接轴更换为国产SWP285（公称转矩90kN·m，疲劳转矩45kN·m，轴线转角15°）。