微分中值定理常见题型的解题方法

曹金亮，谢锦涛

(1.浙江海洋学院数理与信息学院,浙江舟山 316022;2.浙江海洋学院东海科学技术学院,浙江舟山 316000)

微分中值定理常见题型的解题方法

曹金亮1，谢锦涛2

(1.浙江海洋学院数理与信息学院,浙江舟山 316022;2.浙江海洋学院东海科学技术学院,浙江舟山 316000)

微分中值定理建立了导数与函数的关系.与微分中值定理有关的常见题型在高等数学的学习中占有重要的地位,构造辅助函数是证明微分中值定理和解题的主要方法,可以起到化繁为简,大大降低解题难度的效果.本文主要介绍与微分中值定理有关的常见题型的解题方法.

微分中值定理;辅助函数;常见题型

1 绪论

微分中值定理建立了导数与函数之间的联系,是应用导数的局部性质研究函数整体性质的重要工具,其中构造辅助函数是解决微分中值定理中证明的关键,但也是解题的困难所在,熟练掌握部分构造法及其几种常用的题型,对解题能力和发散性思维的培养有一定促进作用.几个主要的微分中值定理如下:

1.1 (Rolle中值定理)[1]如果函数f（x）满足

(1)在闭区间［a，b］上连续;

(2)在开区间（a，b）内可导;

(3)在区间端点处的函数值相等,即f（a）=f（b）;

那么在（a，b）内至少有一点ζ（a＜ζ＜b）,使得f（ζ）=0.

1.2 (Lagrange中值定理)[1]如果函数f（x）满足

(1)在闭区间上［a，b］连续;

(2)在开区间内（a，b）可导,

那么在（a，b）内至少有一点ζ（a＜ζ＜b）,使等式f（b）-f（a）=f＇（ζ）（b-a）成立.

1.3 (Cauchy中值定理)[1]如果函数f（x）及g（x）满足

(1)在闭区间上0［a，b］连续;

(2)在开区间内（a，b）可导;

(3)对任一x∈（a，b）,g＇（x）≠0,

2 微分中值定理的应用

2.1 罗尔中值定理的应用

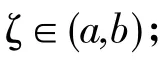
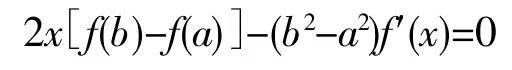
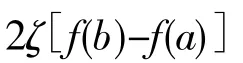
注:此类题型因含中值ζ的两项已分居在中值等式的两旁,其他各项均为常数,而这两项导数又可倒用导数公式求出其原函数,便可求出辅助函数F（x）:

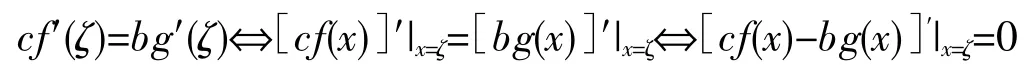
令F（x）=c·f（x）-b·g（x）即为所求的辅助函数.

例2:设函数f（x）在［1，2］上连续,在（1，2）内可导,且f（2）=0,证明至少有一点∈（1，2）,使

证明:取g（x）=ln x,则有［f（x）g（x）］＇=［f（x）ln（x）］＇=f＇（x）ln（x）+（ln x）＇f（x）=0.

注:常利用导数公式［f（x）g（x）］＇=f（x）g＇（x）+f＇（x）g（x）找出辅助函数F（x）=f（x）g（x）.

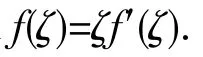
(4)题型四[2]:研究函数或导数所对应的方程根的个数.

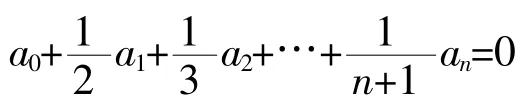
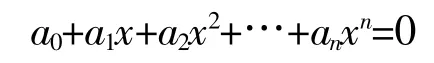
在（0，1）内至少有一个实根.

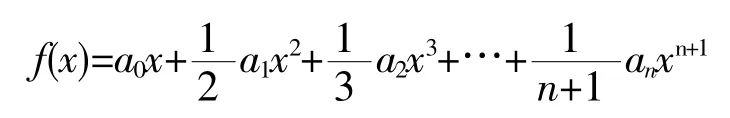
则f（x）在[0，1]上连续,在（0，1）内可导,且f（0）=f（1）=0,于是由罗尔定理即可得证.

注:此类题型常常从所要证明的结论入手.

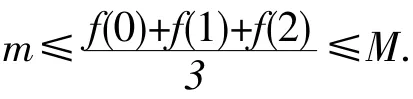
注:该题型的特点是除给出区间端点a,b的函数值外,还给出(或能求出)另一点的函数值,且找出辅助函数F（x）后,一般不满足F（a）=F（b）,此时一般通过介值定理再找F（x）的一个零点,最后在小区间内对F（x）使用罗尔中值定理,使问题得到解决.

2.3 拉格朗日中值定理的应用

(1)题型六:证明与函数差值有关的中值命题.

例6:设f（x）在[a，b]上可导,且ab＞0,试证:存在ζ∈（a，b）,使

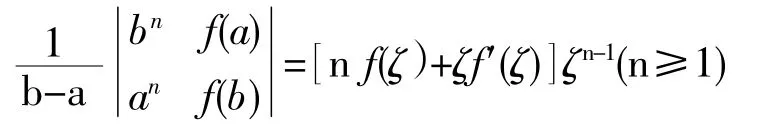
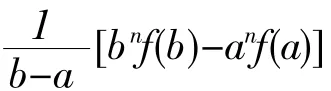
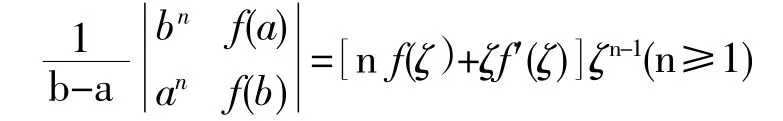
(2)题型七:证明含有或可化为函数差值的不等式.

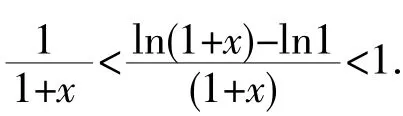
注:这类不等式常用拉格朗日中值定理证明,有时为了构造函数改变量常利用函数性质及f（0）=0的条件作恒等变形或在等式中增添一项及相反项,或增添其值恒为零的常数项如ln1,sin0为使用拉格朗日中值定理创造条件.

(3)题型八:用来求极限.

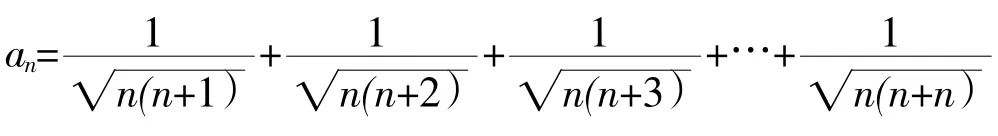
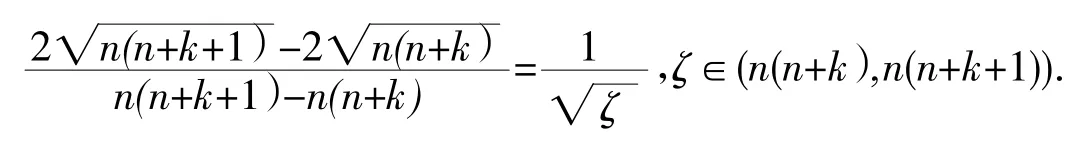
故

当k=0，1，2，…,n-1时,共有n个不等式,将这n个不等式相加得:

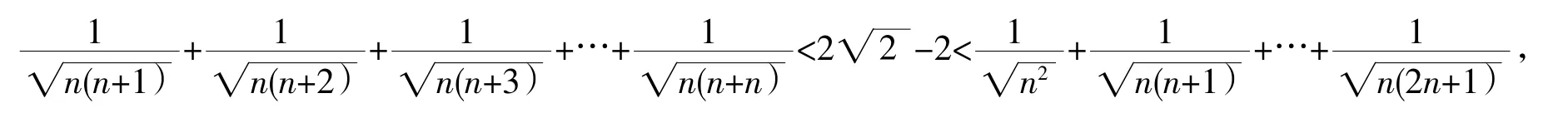
即

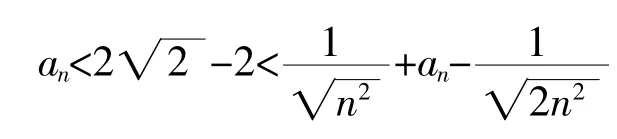
从而

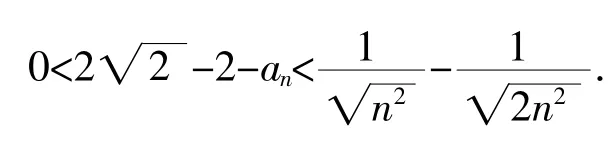
注:求数列极限问题时,运用辅助函数法、递推法和累加法等,往往可使问题得到解决.在应用微分中值定理时,仔细观察、认真分析,适当变换待证明的式子巧妙构造辅助函数是解题的关键.

2.4 柯西中值定理的应用

(1)题型九[4]:证明两函数差值之比的等式(若表达式关于端点处的函数值具有对称性常可利用常数K值法）

例10:设f（x）函数在[a，b]上连续,在（a，b）内可导,试证明存在∈（a，b）,使

例12:设g（x）＞0,g＇（x）≠0（a≤x≤b）,则存在ζ∈（a，b）,使得

注:在构造函数时,若表达式关于端点处的函数值具有对称性,通常用常数K值法来求构造辅助函数,这种方法一般选取所证等式中不含ζ的部分作为K,即使常数部分分离出来并令其为K,恒等变形使等式一端为a与f（a）构成的代数式,另一端为b与f（b）构成的代数式,将所证等式中的端点值(a或b)改为变量x,移项即为辅助函数F（x）,再用中值定理或待定系数法等方法确定K.

(2)题型十:证明两函数导数之比的中值等式

例11:设f（x）在[0，x]（x＞0）上连续,在（0，x）内可导,且f（0）=0.试证明在（0，x）内存在ζ,使f（x）=（1+ζ）f＇（ζ）ln（1+x）.

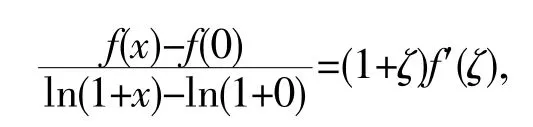
说明:待证等式也可化为左端为函数f（x）与ln（1+x）在两点的差值比.同样可以想到对f（x）,ln（1+x）在[0，x]上使用柯西中值定理来完成证明.

注:这类题型中两函数的导数至少其中之一没有给出,往往需凭想象,倒用导数公式求出.

3 结论

微分中值定理在高等数学中占有很重要的地位,与之有关的题目也是学习与应试的重点和难点.本文对与微分中值定理有关的常见题型的进行了归纳和总结,对各种题型如何构造辅助函数进行了提炼,使我们在解题时能做到思路清晰、胸中有数.

[1]同济大学数学系.高等数学上册（第六版）[M].北京:高等教育出版社,2007.

[2]应六英.中值定理证明的归一性及应用[J].江西电力职业技术学院学报,2004,17（1）：37.

[3]朱智和.微分中值定理在解题中的若干应用[J].绍兴文理学院学报:自然科学版,2009,29（10）：116.

[4]唐 帅,王志华.微分中值定理证明题中辅助函数的构造方法[J].邵阳学院学报:自然科学版,2009,6（4）：27-28.

Common Approaches to Problem s Related to M ean Value Theorem of Differentials

CAO Jin-liang1,XIE Jin-tao2
（1.School of Mathematics，Physics and Information Science，Zhejiang Ocean University，Zhoushan 316000；2.Donghai School of Science and Technology，Zhejiang Ocean University，Zhoushan 316022，China）

One theorem of particular significance in advanced mathematics is the Mean Value Theorem of Differentials（for short，MVTD）which establishes a relation between functions and their derivatives.The Construction of auxiliary functions in proving MVTD greatly simplifies the problems.This paper introduces some common approaches to problems related to MVTD.

Mean Value Theorem of Differentials；auxiliary functions；common problems

O172.1

A

1008-830X（2014）05-0478-05

2014-02-03

曹金亮(1971-),男,江西上饶人,讲师,博士研究生,研究方向:交能信息工程及控制.