载荷不确定条件下的结构拓扑优化算法

赵军鹏 王春洁

(北京航空航天大学 机械工程及自动化学院，北京100191)

结构拓扑优化通常是在给定的载荷工况下寻找材料的最佳分布.然而外界载荷一般存在不确定性，在确定性载荷工况下获得的最优结构形式通常在抵抗载荷扰动时是比较脆弱的，因此有必要研究在载荷不确定条件下的结构拓扑优化问题.现阶段通常采用概率方法和非概率方法表示载荷的不确定性[1].概率方法通过指定载荷的概率分布来表示其不确定性，而非概率方法则通过指定载荷允许的变化范围来表示其不确定性.在结构拓扑优化中，概率方法通常要求结构在不确定载荷作用下柔度的均值与方差最小，而非概率方法则要求结构的最大柔度最小.对于非概率载荷不确定性问题，一般利用椭球表示其不确定性，然后将最大最小问题转化为半定规划形式的优化模型进行求解[2－4];对于概率载荷不确定性问题，求解难度则集中在如何有效计算结构柔度的均值与方差以及它们对设计变量的灵敏度[5－6].结构柔度均值的计算已经出现较为有效的方法[5，7]，然而其方差的计算问题还没有得到很好的解决.对于桁架结构，针对载荷各分量服从多元正态分布的情形已给出了结构柔度均值与方差的解析表达式，并基于此发展了考虑柔度方差的拓扑优化方法[6]，但是实际工程中载荷的不确定性通常采用载荷大小和作用方向描述，载荷各分量一般不服从多元正态分布.对于连续体结构，针对载荷大小不确定的情形同样发展了结构拓扑优化方法[8]，但由于未考虑载荷方向不确定性，因此在实际工程中可以应用的情形有限.

本文针对载荷不确定条件下以结构柔度均值与标准差的加权和最小为目标的连续体结构拓扑优化问题，首先利用线弹性结构的位移叠加原理给出结构柔度均值与方差的计算公式，其次在此基础上给出结构灵敏度分析方法，然后给出载荷不确定条件下的结构拓扑优化算法，最后通过算例说明本文方法的有效性以及考虑载荷不确定性的结构拓扑优化结果的稳健性.本文的讨论基于平面结构问题，但很容易推广到三维情形.

1 载荷不确定条件下的结构拓扑优化问题

本文采用密度法进行连续体结构拓扑优化问题的求解，并采用约束最小刚度的插值模型将单元的材料属性Ee与单元密度ρe联系起来[9]:

其中，E0为材料的弹性模量;Emin是为了防止刚度矩阵奇异而赋予无材料单元的很小的刚度值;p≥1为惩罚因子，可以迫使单元密度在优化过程中取值趋向0或1，从而获得构型清晰的结构.

假设结构被离散为N个单元，单元e的体积为ve，密度为ρe.则载荷不确定条件下的连续体结构拓扑优化问题可以表示为

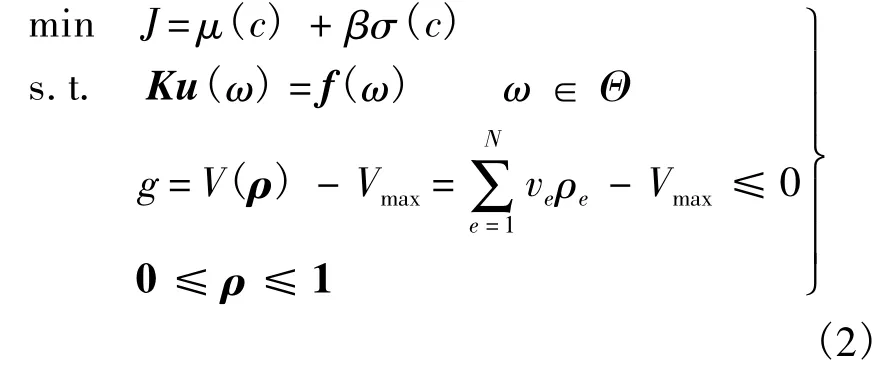
其中，μ(c)与σ(c)分别为结构柔度的均值和标准差;非负常数 β用于权衡σ(c)的重要性;Ku(ω)=f(ω)为结构的有限元平衡方程;ω∈Θ表示载荷具有不确定性，ω为概率空间Θ上的任意实现;Vmax为许用材料体积;ρ为由各单元密度组成的设计变量向量.

2 结构柔度均值与方差的计算

假设结构承受n个不确定载荷，并且每个载荷的大小hi和作用方向与x方向的夹角θi的概率分布均已知.设f2i－1和f2i分别为单独在第i个不确定载荷作用点沿x方向和沿y方向施加单位载荷时的整体载荷向量，并且在f2i－1和f2i作用下结构的位移向量分别为u2i－1和u2i，则根据叠加原理，对于任意的载荷:

相应的结构位移为

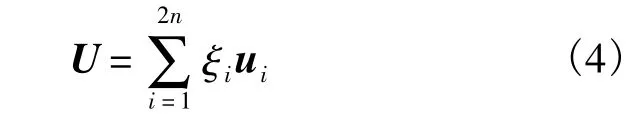
其中

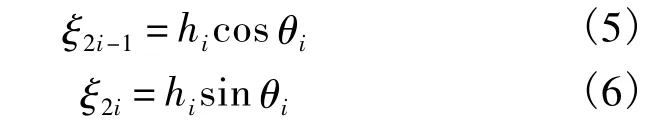
从而结构的柔度为

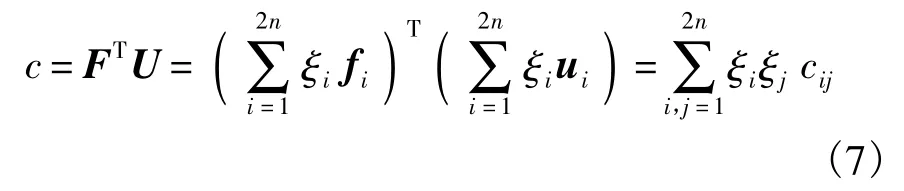
为了书写简洁，在下面的讨论中记m=2n，并引入ξi的二阶和四阶中心矩:

ξij与ξijkl的解析表达式通常很难给出，但可以通过蒙特卡罗方法对它们的值进行精确估计.

结构柔度的均值为结构在各种可能载荷工况下柔度的期望:

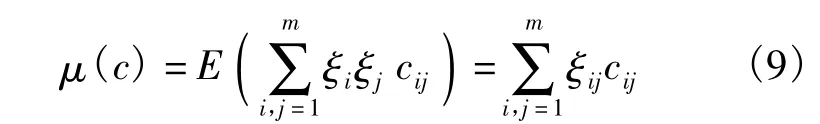
结构柔度的方差可以表示为结构在各种可能载荷工况下柔度平方的期望与结构柔度均值的平方之差:

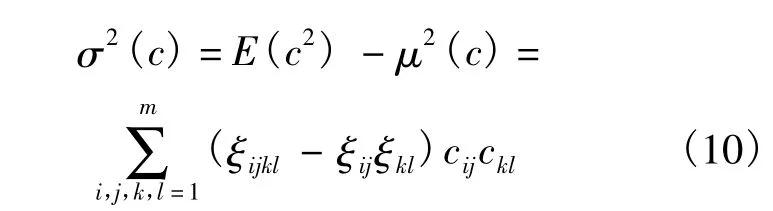
由此可知，在ξij与ξijkl已知的情况下，只要获得结构在载荷工况f1，f2，…，fm作用下的位移向量u1，u2，…，um，就可以求得结构柔度的均值与方差，而并不需要对所有可能工况进行结构分析.注意到cij为向量fi与uj的内积，因此相对于结构有限元分析，其计算量可以忽略不计.

3 结构灵敏度分析

根据式(9)和式(10)可知，结构柔度均值与标准差对密度ρe的偏导数分别为

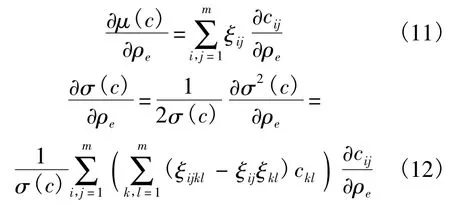
引入变量:

则目标函数对ρe的偏导数为

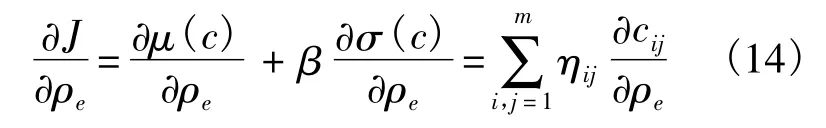
利用拉格朗日乘子法容易证明:

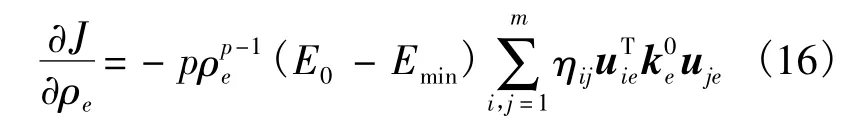
体积约束对于设计变量的灵敏度为

4 载荷不确定条件下的结构拓扑优化算法

综合以上内容可以给出载荷不确定条件下的结构拓扑优化算法，其流程如图1所示.首先利用蒙特卡罗方法计算ξij与ξijkl;然后离散设计域并初始化设计变量;在此基础上对结构进行多载荷工况有限元分析;根据有限元分析结果计算结构柔度均值与方差并进行灵敏度分析;为了消除结构拓扑优化过程中经常出现的棋盘格等现象，采用灵敏度过滤器[10]对灵敏度信息进行过滤，然后利用移动渐近线[11]方法更新设计变量并判断优化过程是否收敛.若收敛，则迭代结束;否则重新进行有限元分析等直至优化过程收敛.

从图1中可以看出，在载荷不确定条件下进行结构拓扑优化，如果承受n个不确定载荷，则每次迭代需要对2n个工况进行有限元分析，而不考虑载荷不确定性时则仅需要进行单个工况有限元分析.因此载荷不确定条件下的结构拓扑优化算法计算量要大于确定性条件下的结构拓扑优化算法.

图1 载荷不确定条件下的结构拓扑优化流程

5 数值算例

本节以两个算例来说明载荷不确定条件下的最优结构与确定条件下的最优结构不同，并且前者要比后者能够更好地抵抗载荷的扰动.两个算例均采用单位双线性正方形单元对设计域进行离散.蒙特卡罗方法计算 ξij与 ξijkl时样本数目为1000000.实体与空单元的弹性模量分别为E0=1，Emin=10－9，材料的泊松比 μ 均为 0.3，惩罚因子p=3.优化结束的准则为每个单元的伪密度变化量均不超出0.01.

5.1 简单立柱结构的拓扑优化

如图2a所示，问题的设计域为100×100的矩形区域，底部边界固定，结构顶端中心承受不确定载荷F.该载荷的大小为10，作用方向与水平方向的夹角服从均值为－π/2(竖直向下)，标准差为π/48的正态分布.材料的许用体积为设计域的20%.

结构拓扑优化结果如图2b～图2d所示.载荷确定条件下材料全部聚集在载荷作用线附近，形成立柱状结构，这与工程直觉相符，但该结构的水平方向承载能力比较弱.考虑载荷不确定性得到的结构均类似于两个顶端相交杆件组成的结构，这样的结构虽然竖直方向承载能力有所下降，但是水平方向承载能力却得到很大提高，从而增强了结构的稳健性.

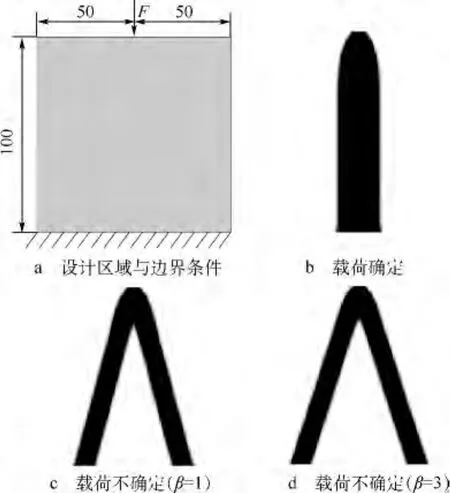
图2 拓扑优化设计区域及不同条件下的优化结果

结构拓扑优化过程收敛曲线如图3所示，优化结果的目标函数值如表1所示.

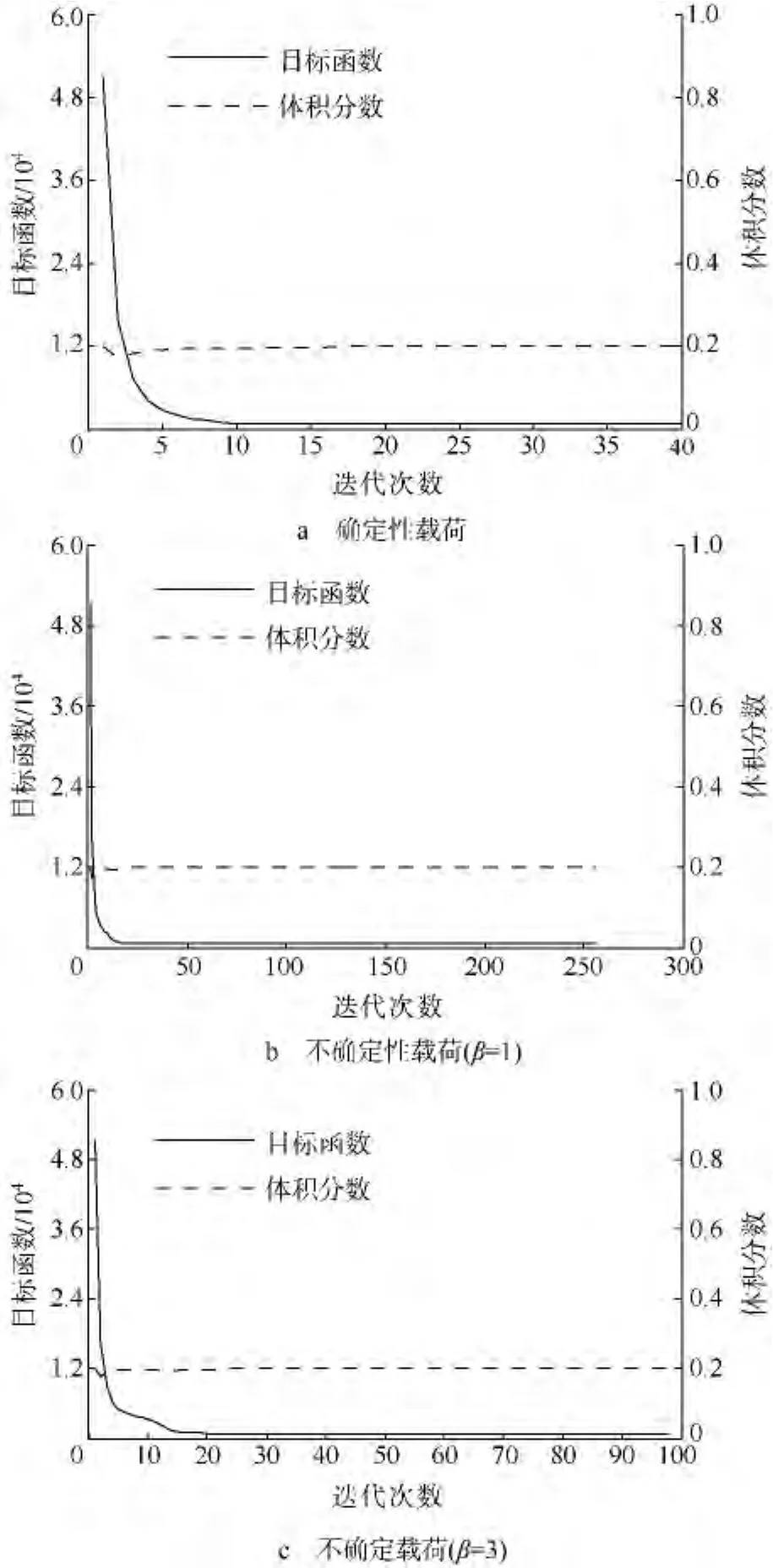
图3 简单立柱结构拓扑优化收敛曲线

表1 简单立柱结构优化结果的目标函数值

可以看出，确定性载荷条件下得到的优化结果在考虑载荷不确定性时的目标函数值要高于不确定载荷条件下得到的优化结果的目标函数值，这证明了本文算法的有效性.

载荷不确定性条件下的最优结构与优化目标中柔度标准差的权重有关，权重增大，两个杆件之间的夹角也增大，结构柔度由于载荷不确定性而引起的波动会减小，但是柔度均值可能会加大.鉴于篇幅的限制，本文不对β如何合理取值的问题进行深入讨论.

5.2 米歇尔结构的拓扑优化

如图4a所示，问题的设计域为240×120的矩形区域，底部两端均简支，并且承受3个不确定载荷 P1，P2，P3.3 个载荷的大小 hi和作用方向与水平方向夹角θi均服从正态分布，它们的均值μhi，μθi和标准差σhi，σθi如表 2 所示.材料的许用体积为设计域的30%.

表2 载荷大小和方向的均值与标准差

取目标函数中的权重β=1，结构拓扑优化结果如图4所示.由于结构的设计域、边界条件以及作用载荷均左右对称，因此优化后的结构也均左右对称.其中只考虑载荷大小不确定性时获得的结构与载荷确定条件下获得的结构构型基本一致，同时考虑载荷大小与方向不确定性时获得的结构与只考虑载荷方向不确定性时获得的结构构型基本一致.对本例而言，载荷方向不确定性比大小不确定性对结构的影响更大.考虑载荷方向不确定性得到的结构中间两根较粗的杆件直径有所减小，两根较细的杆件与水平方向的夹角也变小，而其下方呈现出连接左右两个端点以及3个载荷作用点的杆件.这样的结构虽然竖直方向承载能力有所下降，但是却更加稳健.这是由于载荷作用方向的不确定性，其可能含有水平方向分量，而水平方向杆件具有较好的承受水平方向载荷的能力，其存在使得结构可以更好地抵抗载荷的不确定性，从而使得结构更加稳健.

图4 米歇尔结构拓扑优化问题及优化结果

结构拓扑优化过程收敛曲线如图5所示，优化结果的目标函数值如表3所示.

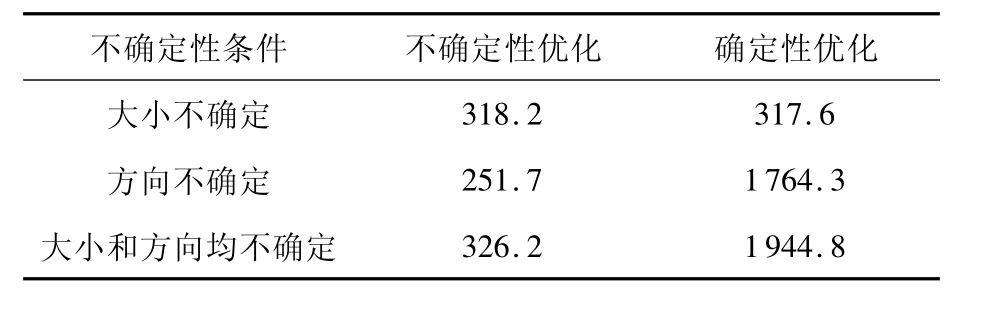
表3 米歇尔结构优化结果的目标函数值

可以看出，确定性载荷条件下得到的优化结果在考虑载荷不确定性时的目标函数值一般高于不确定载荷条件下得到的优化结果的目标函数值，这证明了本文算法的有效性.注意到载荷大小不确定条件下优化结果的目标函数值与确定条件下优化结果的目标函数值相差不超过0.5%，二者的优化结果也几乎相同.

图5 米歇尔结构拓扑优化收敛曲线

6 结论

1)与确定性载荷作用下的结构拓扑优化方法相比，本文方法得到的优化结果在载荷不确定条件下具有更小的柔度均值和方差，因此更加稳健;

2)优化目标中柔度均值与标准差的相对权重对结构拓扑优化结果有较大影响;

3)对于本文中的算例，相对于载荷大小不确定性，方向不确定性对优化结果有更显著的影响.

致谢 衷心感谢瑞典皇家理工学院的Krister Svanberg教授提供移动渐近线法的代码.

References)

[1]Calafiore G C，Dabbene F.Optimization under uncertainty with applications to design of truss structures[J].Structural and Multidisciplinary Optimization，2008，35(3):189 －200

[2]Ben-Tal A，Nemirovski A.Robust truss topology design via semidefinite programming[J].SIAM Journal on Optimization，1997，7(4):991－1016

[3]李东泽，于登云，马兴瑞.不确定载荷下的桁架结构拓扑优化[J].北京航空航天大学学报，2009，35(10):1170 －1173

Li Dongze，Yu Dengyun，Ma Xingrui.Truss topology optimization with uncertain loading scenarios[J].Journal of Beijing University of Aeronautics and Astronautics，2009，35(10):1170 － 1173(in Chinese)

[4]De Gournay F，Allaire G，Jouve F.Shape and topology optimization of the robust compliance via the level set method [J].Esaim-Control Optimisation and Calculus of Variations，2008，24(1):43－70

[5]Alvarez F，Carrasco M.Minimization of the expected compliance as an alternative approach to multiload truss optimization[J].Structural and Multidisciplinary Optimization，2005，29(6):470－476

[6]Carrasco M，Ivorra B，Ramos A.A variance-expected compliance model for structural optimization[J].Journal of Optimization Theory and Applications，2012，152(1):136 －151

[7]Dunning P D，Kim H A，Mullineux G.Introducing loading uncertainty in topology optimization[J].AIAA Journal，2011，49(4):760－768

[8]Dunning P D，Kim H A.Robust topology optimization:minimization of expected and variance of compliance[J].AIAA Journal，2013，50(11):2656 －2664

[9]Andreassen E，Clausen A，Schevenels M，et al.Efficient topology optimization in MATLAB using 88 lines of code[J].Structural and Multidisciplinary Optimization，2011，43(1):1 －16

[10]Sigmund O.On the design of compliant mechanisms using topology optimization[J].Mechanics of Structures and Machines:An International Journal，1997，25(4):493 － 524

[11]Svanberg K.The method of moving asymptotes:a method for structural optimization[J].International Journal for Numerical Methods in Engineering，1987，24(2):359 －373