采煤机行走机构啮合参数对动力学特性的影响
2014-11-03吴卫东张志飞
吴卫东, 张志飞
(黑龙江科技大学 机械工程学院, 哈尔滨 150022)
采煤机行走机构啮合参数对动力学特性的影响
吴卫东,张志飞
(黑龙江科技大学 机械工程学院, 哈尔滨 150022)
为提高薄煤层采煤机行走机构工作平稳性,分析两销轨间节距及摆线轮与销轨中心距啮合变化的影响,建立了相应的数学模型,应用ADAMS软件分析不同啮合参数对行走机构动力学特性的影响。结果表明:在最小节距118.5 mm时,当摆线轮与销轨前齿啮出,后齿还未进入啮合时,发生速度突降;在最大节距131.5 mm时,当中心距为理论值139.27及变化±10 mm时,其最大速度与啮合力分别是节距为125 mm、中心距139.27 mm理论条件下的1.29、1.24及1.60倍与1.57、1.37及2.48倍,中心距减小要比中心距增大时所引起速度与啮合力波动大。为减小牵引速度等波动量,建议在设计该机构时,中心距在理论值基础上可增加2~3 mm。
薄煤层采煤机; 行走机构; 动力学分析; ADAMS
0 引 言
我国薄煤层储量占煤炭总量的20%左右,由于其开采条件等原因,导致薄煤层开采的自动化及生产效率普遍较低,产量仅占7%左右[1-2]。薄煤层工作面采高低,要求采煤机机身矮且尽可能短,以适应煤层起伏变化,且需要有足够的过煤和过刮板输送机高度[3]。由于受开采空间限制,薄煤层采煤机整机结构需要更加紧凑。行走机构作为薄煤层采煤机的重要组成部分,主要承担整个采煤机的行走和导向作用。行走机构在工作过程中由于受到摆线轮与销轨啮合冲击的影响,常会造成行走轮失效及其他传动机构的损坏,导致其传动失效,影响采煤机的正常工作[4-5]。王振乾对采煤机行走机构进行运动学分析,得到其中心距和中心高变化对其运动学特性的影响[6]。笔者对采煤机摆线轮-销轨无链牵引机构进行运动分析,得出中心距及节距变化对啮合传动特性的规律[7];由于薄煤层采煤机行走机构中摆线轮齿数较少,容易产生较大的速度波动和冲击载荷。因此,对薄煤层采煤机行走机构进行动力学分析有着非常重要的意义,文中应用ADAMS软件模拟两销轨间节距以及摆线轮与销轨啮合中心距变化对行走机构动力学特性的影响。
1 行走机构的传动模型
1.1摆线轮的轮廓
目前,采煤机行走轮常用的轮齿齿廓主要有摆线和渐开线两种。薄煤层采煤机行走轮齿郭通常采用摆线形成,其轮齿齿廓的曲线生成原理,如图1所示。其中摆线轮模数m=39.79 mm、z=7,基圆半径R=mz/2=139.27 mm。外、内滚动圆半径分别为
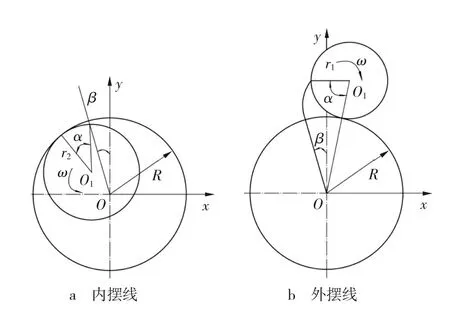
图1 摆线轮齿廓
r1=70 mm、r2=87.5 mm,摆线轮节圆齿厚δ=60 mm,内、外圆沿固定圆内、外表面纯滚动所转过的角度分别为α和β。
内摆线齿廓曲线方程:
(1)
外摆线齿廓曲线方程:
(2)

(3)
1.2摆线轮与Ⅰ型销轨
针对某型号薄煤层采煤机,行走机构采用的Ⅰ型销轨,如图2所示。

图2 Ⅰ型销轨
根据式(1)~(3),运用Pro/E软件建立行走机构中摆线轮三维实体,如图3所示。
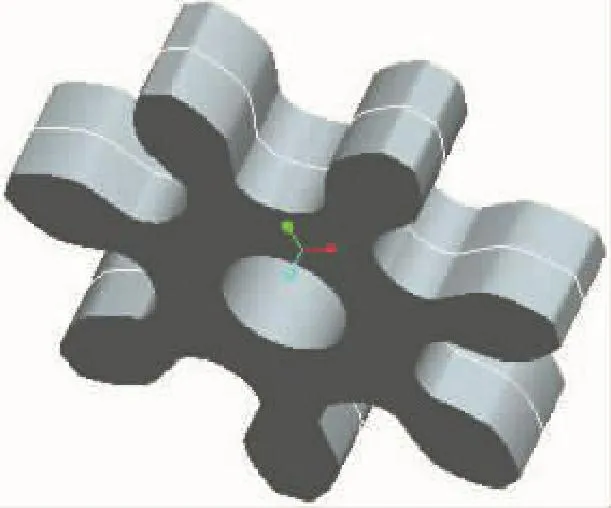
图3 摆线轮三维实体
2 行走机构的动力学仿真
行走机构在工作过程中,除受到机身重力、牵引力等基本载荷,还受到其他冲击载荷,导致行走轮在工作过程中出现严重磨损甚至断裂。文中采用多体动力学软件ADAMS,应用Hertz弹性碰撞理论来模拟行走机构的动力学特性。
2.1仿真模型
将建立的行走机构模型导入ADAMS中,参考齿轮齿条传动的约束方式,添加相应约束[8-11],分别为
(1)摆线轮上添加转动副,选择大地为机架;
(2)销轨添加移动副,选择大地为机架;
(3)摆线轮与销轨啮合处添加实体碰撞力。
为了更好地分析两销轨连接处动力学特性,避免产生较大的冲击,在施加转速驱动和牵引阻力时均采用STEP函数,在0.2 s内平缓变化,ADAMS中所建立的行走机构模型,如图4所示。

图4 摆线轮-销轨添加约束
2.2模拟工况类型
通常情况下,刮板输送机可沿工作面起伏±3°,故根据销排安装结构特性,其可沿工作面±1.5°倾角变化;另外,考虑销排连接U型销孔间隙,导致行走机构节距l变化±6.5 mm和中心距h变化±10 mm。为此在对行走机构进行仿真分析时,对理论工况与两销轨间最小、最大节距分别为118.5与131.5 mm,理论中心距139.27 mm及变化±10 mm时行走机构的动力学变化规律进行分析。仿真啮合参数,如表1所示。

表1 仿真啮合参数
3 仿真结果
采煤机牵引功率为30 kW,在摆线轮上施加最大角速度为6.86 rad/min,对该机构进行仿真分析,为避免因仿真步长等原因而造成仿真结果失真,对仿真结果进行平滑和滤波处理。
3.1理论工况
行走机构在标准节距125.0 mm、中心距139.27 mm理论工况下仿真结果,如图5所示。
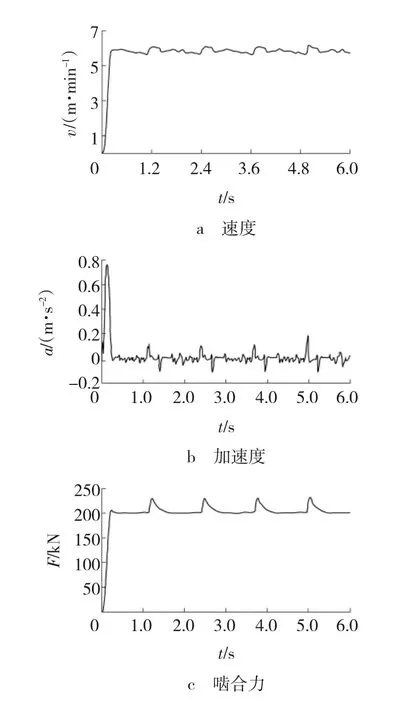
图5 理论工况的仿真曲线
由图5可见,行走机构在稳定工作状态下,速度围绕均值5.87 m/min做周期性变化,其相对于理论值误差为2.17%,速度最大值vmax为6.13 m/min,最小值vmin为5.57 m/min,加速度a最大值为0.19 m/s2;啮合力最大值Fmax为228.45 kN,最小值Fmin为200.03 kN。
3.2最小节距
当工作中相邻两销轨连接处最小节距为118.5 mm,中心距分别为139.27、129.27及149.27 mm时,仿真结果如图6~8所示。

图6 中心距139.27 mm的仿真曲线
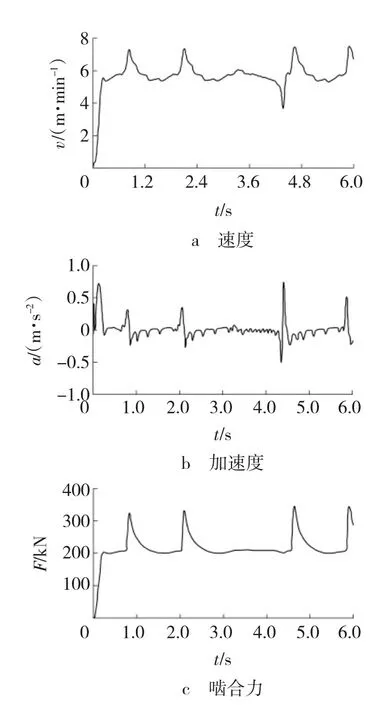
图7 中心距129.27 mm的仿真曲线
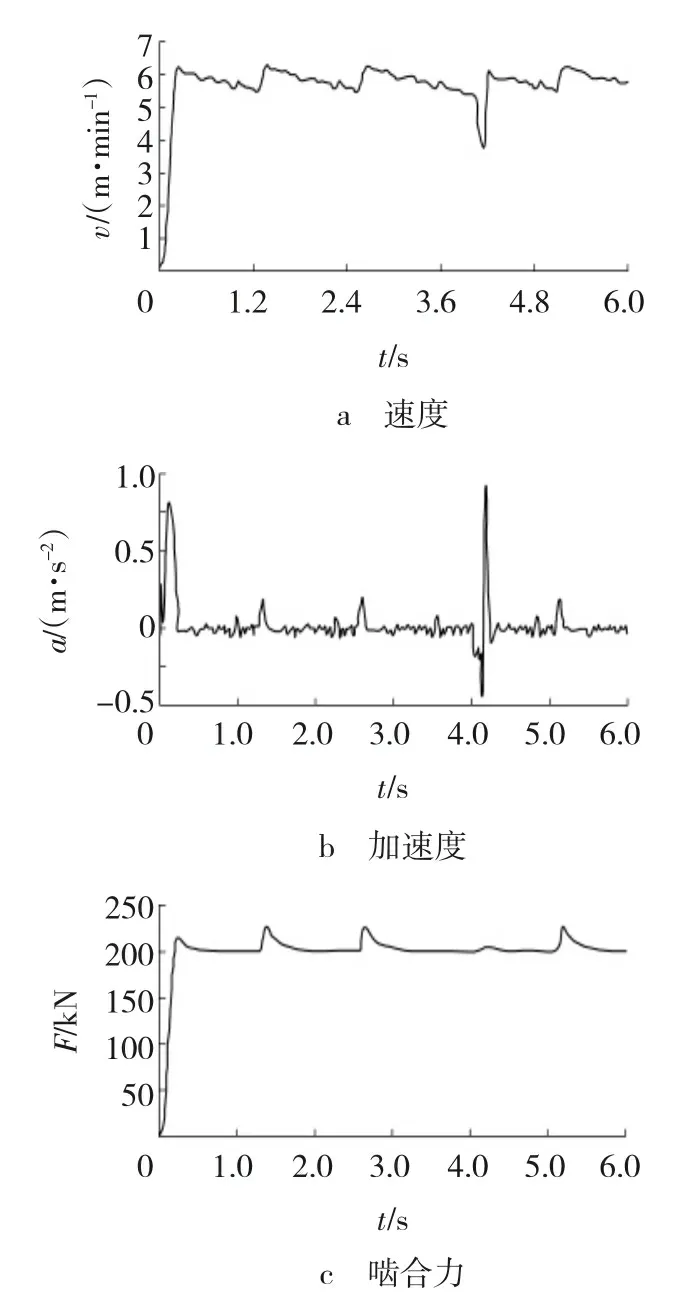
图8 中心距149.27 mm的仿真曲线
由图6~8可见,行走机构在稳定工作状态下,与单一销轨啮合,速度、加速度及啮合力均呈周期性变化。在两销轨连接处最小节距为118.5 mm时,发生速度突降,在理论中心距139.27及变化±10 mm时,最小速度分别为4.18、3.89和3.66 m/min;最大加速度值分别为0.68、0.91和0.77 m/s2。
3.3最大节距
当工作中相邻两销轨间连接处最大节距为131.5 mm,中心距分别为139.27、129.27及149.27 mm时的仿真结果如图9~11所示。
由图9~11可见,行走机构在稳定工作状态下,与在单一销轨啮合,其速度、加速度及啮合力均呈周期性变化。当两销轨连接处最大节距为131.5 mm时,由于摆线轮提前与销轨进入啮合,会造成较大的速度波动和冲击载荷,在中心距为139.27mm及变化±10 mm时,其速度最大值分别为7.89、7.58和9.76 m/min;加速度最大值分别为0.71、0.60和1.71 m/s2;啮合力最大值分别为357.93、313.88和567.58 kN。
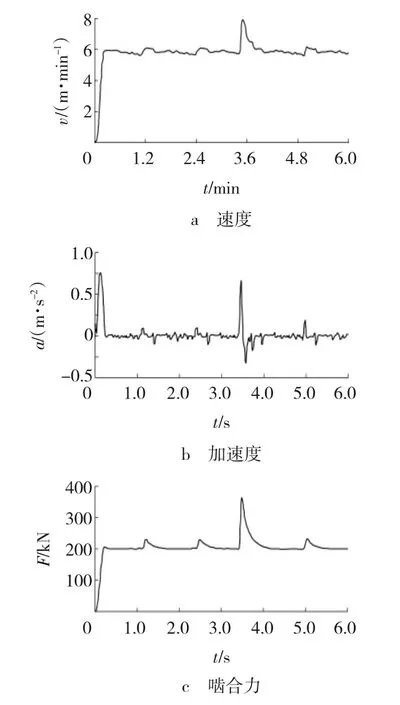
图9 中心距139.27 mm的仿真曲线
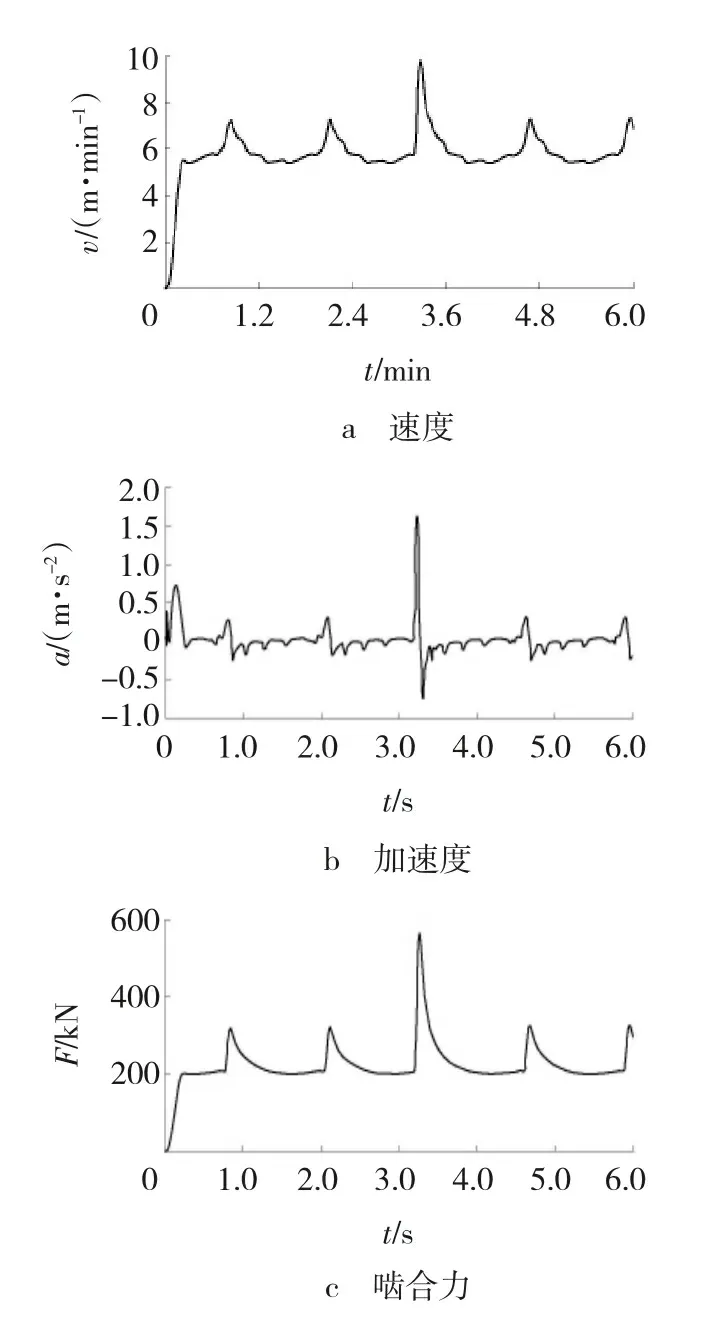
图10 中心距129.27 mm的仿真曲线
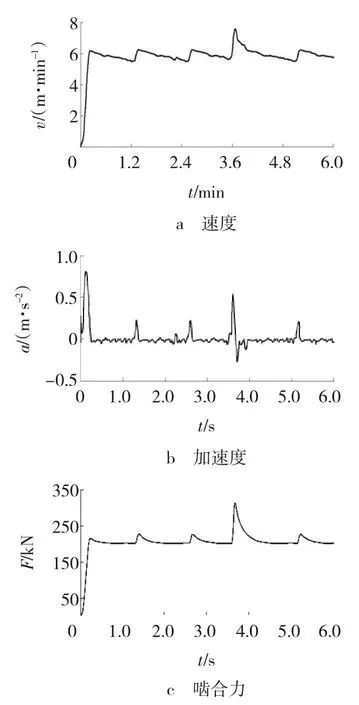
图11 中心距149.27 mm的仿真曲线
4 仿真分析
为了便于分析,列出对行走机构7种工况模拟所得速度和啮合力的特征值,分别如表2和表3所示。

表2 速度特征值
由表2和表3可知,行走机构工作过程中,当销轨节距和摆线轮与销轨啮合中心距发生变化时,会产生较大的牵引速度波动和啮合力变化,对行走机构造成冲击,进而影响其使用寿命。在两销轨连接处最小节距为118.5 mm,中心距为139.27 mm及变化±10 mm时,其速度减小量分别为理论工况下速度均值的29.13%、33.39%及38.16%;在两销轨连接处最大节距为131.5 mm,中心距为139.27 mm及变化±10 mm时,最大速度分别是理论工况的1.29、1.24及1.60倍;啮合力最大值分别为理论工况的1.57、1.37及2.48倍。
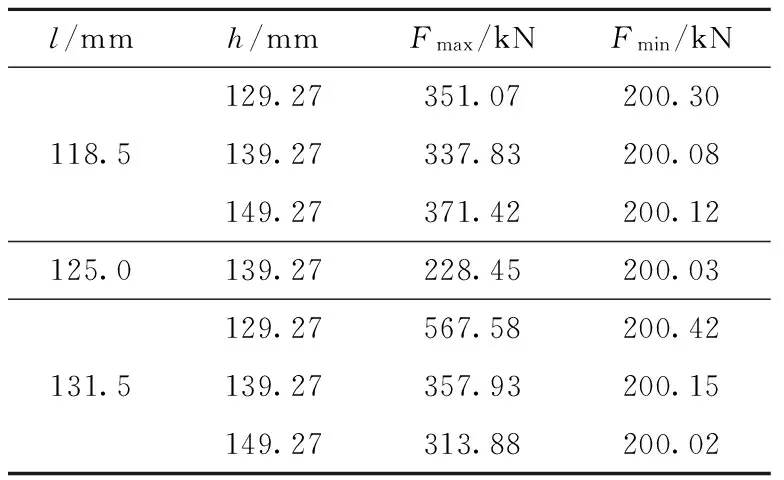
表3 啮合力特征值
为了进一步分析两销轨间节距以及摆线轮与销轨啮合中心距变化对行走机构牵引速度波动的影响,按照上述方法,节距在125~130 mm及中心距在130~152 mm变化时所得的72组仿真数据,利用MatLab软件,绘制如图12所示的牵引速度超调量关系图。
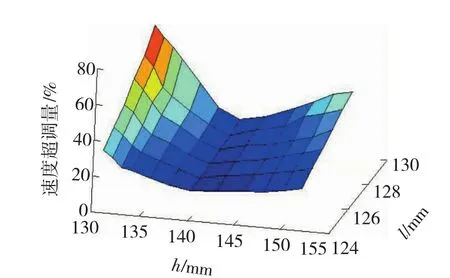
图12 不同节距及中心距变化与牵引速度超调量关系
由图12可见,随着中心距减小或增大,其速度超调量均增大,但中心距减小时,要比中心距增大引起的速度超调量要显著。
5 结 论
(1)在理论条件下,牵引速度均值为5.87 m/min,加速度最大值为0.19 m/s2。当两销轨连接处最小
节距为118.5 mm时,摆线轮与销轨啮合时会发生前齿啮出时,后齿还未进入啮合,导致速度发生突降;中心距为理论值139.27 mm及变化±10 mm时,牵引速度减小均为理论条件下值的1/3左右,瞬间加速度相比理论值变化较大,其分别为1.08、1.37和1.28 m/s2。
(2)当两销轨连接处最大节距为131.5 mm时,由于摆线轮提前与销轨进入啮合,会产生较大的速度波动和冲击载荷;当中心距为139.27 mm及变化±10 mm时,其最大速度与啮合力分别是理论工况的1.29、1.24及1.60倍与1.57、1.37及2.48倍。
(3)中心距的减小对行走机构牵引速度波动的影响要大于其中心距的增大所带来的影响,从减小速度波动量考虑,建议设计该机构时,在理论中心距的基础上可适量增加2~3mm。
[1]徐亚军, 王国法. 基于滚筒采煤机薄煤层自动化开采技术[J]. 煤炭科学技术, 2013, 40(11): 6-9.
[2]乔红兵, 吴淼, 胡登高. 薄煤层开采综合机械化技术现状及发展[J]. 煤炭科学技术, 2006, 34(2): 1-5.
[3]李建平, 杜长龙, 张永忠. 我国薄与极薄煤层开采设备的现状和发展趋势[J]. 煤炭科学技术, 2005, 33(6): 65-67.
[4]杜成林, 张芝侠, 贾龙. 基于ABAQUS的采煤机行走机构啮合动态仿真[J]. 煤矿机电, 2013(5): 66-67.
[5]陈伟, 杜长龙, 夏丽建, 等. 基于 ANSYS Workbench 采煤机行走轮与销轨啮合瞬态动力分析[J]. 矿山机械, 2011, 39(2): 20-23.
[6]王振乾. 滚筒式采煤机行走机构运动学分析及强度研究[D]. 上海: 煤炭科学研究总院, 2007.
[7]吴卫东, 刘春生, 孙月华, 等. 采煤机摆线轮-销排式无链牵引机构运动仿真[J]. 黑龙江矿业学院学报, 1998, 8(3): 29-33.[8]苏艳, 李涛涛, 郭燕. 基于ADAMS的齿轮-齿条变幅驱动动力学研究[J]. 武汉理工大学学报:信息与管理工程版, 2013, 35(6): 856-858.
[9]徐方舟, 魏小辉, 张明, 等. 基于ADAMS 的齿轮齿条刚柔耦合啮合分析[J]. 机械设计与制造, 2012, 7(7): 200-202.
[10]刘春生, 任春平, 李德根. 修正离散正则化算法的截割煤岩载荷谱的重构与推演[J]. 煤炭学报, 2014, 39 (5): 981-986.[11]葛正浩. ADAMS 2007虚拟样机技术[M]. 北京: 化学工业出版社, 2007.
[12]崔景昆, 赵晋洋, 张学峰. 大倾角仰斜综采工艺在郭二庄矿的应用[J]. 河北工程大学学报: 自然科学版, 2008, 28(3): 92-94.
(编辑李德根)
Influence of meshing parameters on dynamics characteristics of shearer’s running gear
WUWeidong,ZHANGZhifei
(School of Mechanical Engineering, Heilongjiang University of Science & Technology, Harbin 150022, China)
This paper proposes a mathematical model of cycloid profile intended to improve the performance stability of the thin seam shearer running gear and specifically identify the influence of pin pitch and center distance on the meshing of cycloid-pin, and offers an analysis of the influence of meshing parameters on the dynamic characteristics of the running gear using ADAMS software. The analysis suggests that cycloidal wheels tend to experience a sudden drop of speed, as occurs when the front teeth is in the state of meshing outside while the rear teeth is out of engagement, in the case of the minimum distance of 118.5 mm;when the max pitch is 131.5 mm and the ideal center distance is 139.27 with a change of ±10 mm, the max speed is 1.29, 1.24 and 1.60 times, and the meshing force is 1.57, 1.37 and 2.48 times, depending on the theoretical condition that the pitch is 125 mm and the center distance is 139.27 mm.The decreased center distance triggers a larger fluctuation in meshing force and speed than does the increased center distance.This is why the reduction of the fluctuation magnitude of traction speed requires a recommended increase of 2~3 mm in center distance on the basis of the theoretical value when it comes to designing the mechanism.
thin seam shearer; running gear; dynamic analysis; ADAMS
2014-04-10
国家自然科学基金面上项目(51274091);黑龙江省自然科学基金项目(E200825)
吴卫东(1967-),男,江苏省沛人,教授,硕士,研究方向:矿山机械设计及理论,E-mail:wu-weidong@163.com。
10.3969/j.issn.2095-7262.2014.03.008
TD421.6
2095-7262(2014)03-0256-06
A
