模拟退火算法在电磁兼容领域的应用
2014-11-02吕明珠刘世勋
吕明珠,刘世勋
(1.辽宁广播电视大学 自控学院,辽宁 沈阳 110043;2.中认(沈阳)北方实验室,辽宁沈阳 110141)
有限元法和线性矩阵法在电磁兼容领域的推广[1],为我们在电磁理论研究、原理剖析、产品电磁设计、产品整改、标准理解、天线参数、接地分析、屏蔽腔体等诸多方面提供技术帮助和理论支撑。但伴随着研究的升级,产品设计、产品整改均亟待解决最优化的问题。电磁领域的最优化就是对于结构、参数的改善达到产品或设备的电磁发射水平最低、工艺最为可行、理论上最为合理的解决方案,这就将本为边缘学科的电磁兼容与智能优化算法第一次有机地结合在一起,使电磁兼容技术服务迈上新的台阶。
1 优化算法
优化算法是通过数值分析和模拟解析的方法得到最优解的计算,针对不同的优化问题,例如可行解变量的取值(连续还是离散)、目标函数和约束条件的复杂程度(线性还是非线性)等,应用不同的算法。对于连续和线性等较简单的问题,可以选择一些经典优化算法,例如梯度、Hessian矩阵、拉格朗日乘数、单纯形法、梯度下降法等;而对于更复杂的问题,则可考虑用一些智能优化算法,例如神经网络、遗传算法、模拟退火法和蚁群算法,此外还包括禁忌搜索、粒子群算法等。智能优化算法和经典优化算法的区别就是,经典优化算法解析速度快捷、简单,但是容易陷入局部最优解,且无法解决非线性问题,而智能优化算法(见图1)虽然算法复杂、收敛条件苛刻,但是其对非线性问题、对无法套用计算公式的问题以及对全局最优解的获取、跳出局部最优解的概率都是经典优化算法所不具备更是无法比拟的。
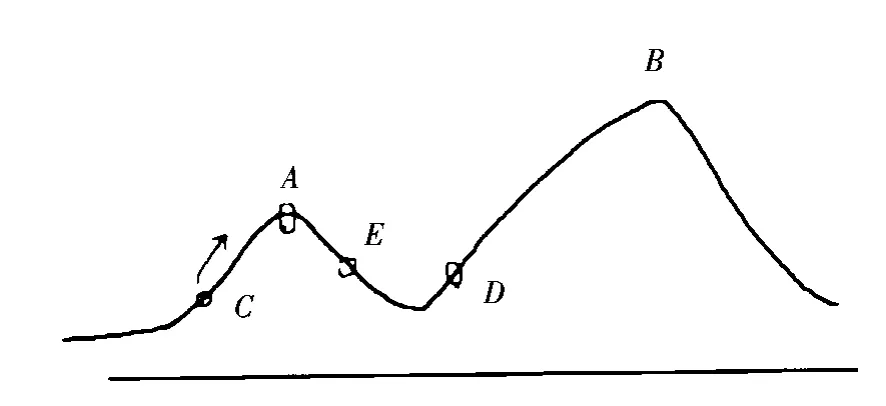
图1 智能优化算法原理图Fig.1 The schematic diagram of intelligent optimization algorithm
1.1 优化算法的选择
随着神经网络和遗传算法研究的深入,随之而来的衍生算法层出不求,尤其是神经网络算法,可以进行超多元的优化计算。但是神经元的训练、突触阈值权加的迭代使寻求全局最优解的过程漫长而复杂;遗传算法同样是收敛困难。为了克服此类弊端,本文引入模拟退火算法,其结构揭开中存有单一变量,引入性价比较高。
1.2 模拟退火法原理
模拟退火算法(Simulated Annealing Algorithm,SAA)是一种通用概率演算法,用来在一个大的搜寻空间内找寻命题的最优解。模拟退火算法可以分解为解空间、目标函数和初始解3部分[2]。
模拟退火算法新解的产生和接受可分为如下4个步骤:第1步是由一个产生函数从当前解产生一个位于解空间的新解;第2步是计算与新解所对应的目标函数差;第3步是判断新解是否被接受,判断的依据是一个接受准则,最常用的接受准则是Metropolis准则:若Δt'<0则接受S'作为新的当前解S,否则以概率exp(-△t'/T)接受S'作为新的当前解S;第4步是当新解被确定接受时,用新解代替当前解,这只需将当前解中对应于产生新解时的变换部分予以实现,同时修正目标函数值即可[3]。
模拟退火算法与初始值无关,算法求得的解与初始解状态S(S是算法迭代的起点)无关;模拟退火算法具有渐近收敛性,已在理论上被证明是一种以概率1收敛于全局最优解的全局优化算法;模拟退火算法具有并行性[4]。
2 电磁兼容应用实例
以实际20英寸液晶显示器为例,模拟其LCD控制电路主芯片对带铆接屏蔽壳主板内部的干扰及耦合情况,使用模拟退火法优化带接地铆接点的个数或密度,以期最大限度的减少或避免谐振频率的出现,目标函数为场强最小[5]。
求解变量为铆钉接地点的个数,而求解域的确定是根据实际加工工艺(20英寸液晶屏屏蔽罩长度约为47 cm,铆钉间距需大于1.5 cm)所能达到的极限,一般为[2,30]内的整数,因此,在2~30个铆钉范围内寻求最优解,其电场强度最小。下面用几组仿真图来说明采用模拟退火算法寻求最优解的过程,图2表示加2个铆钉时的屏蔽罩模型,图3则表示其对应的电场强度分布情况,图中蓝色区域表示电场强度的低能量区,橙色区域表示高能量区,能量区面积越大,表示电磁谐振程度越强。
变更求解变量也就是铆钉数量,计算并重新形成电场强度分布。
图4和图5分别表示加5个铆钉时的屏蔽罩模型及其对应的电场强度分布情况,经过对比图3和图5场强情况,不难发现,带有不同个数铆钉的屏蔽罩在电场强度分布上明显不同,而且相比于2个铆钉屏蔽罩,5个铆钉屏蔽罩的谐振程度明显得到了改善,谐振点分布明显收缩,也反映出该算法朝着电磁发射水平降低的方向进行迭代。
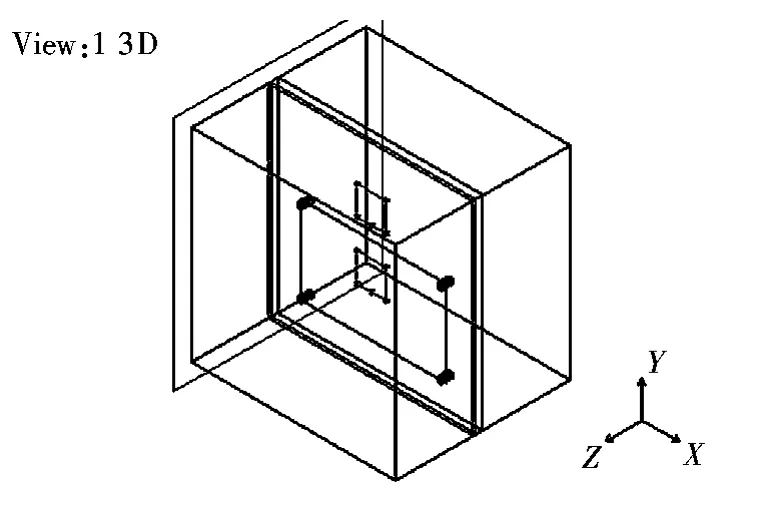
图2 加2个铆钉屏蔽罩示意图Fig.2 The EMC shield with 2 rivets
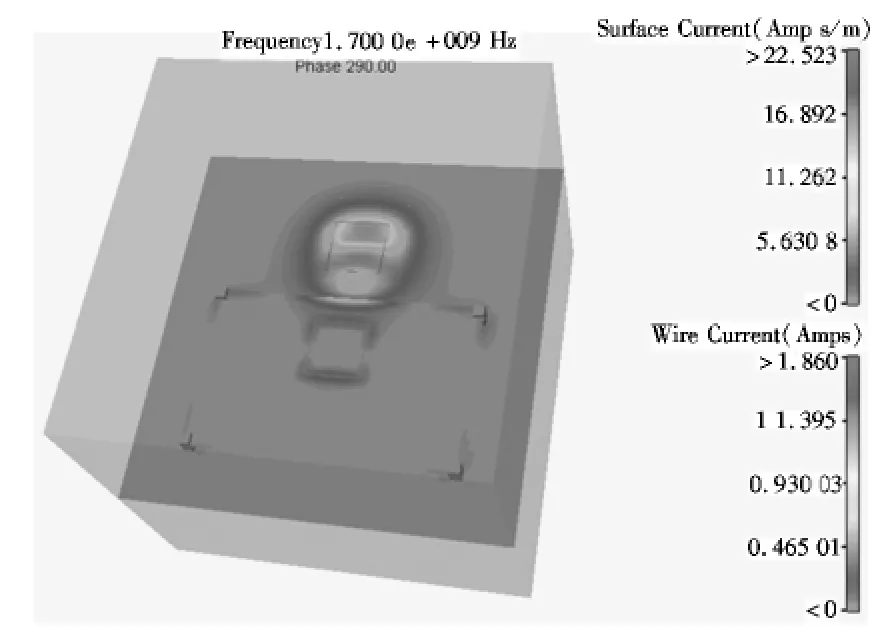
图3 加2个铆钉屏蔽罩电场强度分布图Fig.3 Distribution charts of the electric field intensity for the EMC shield with 2 rivets
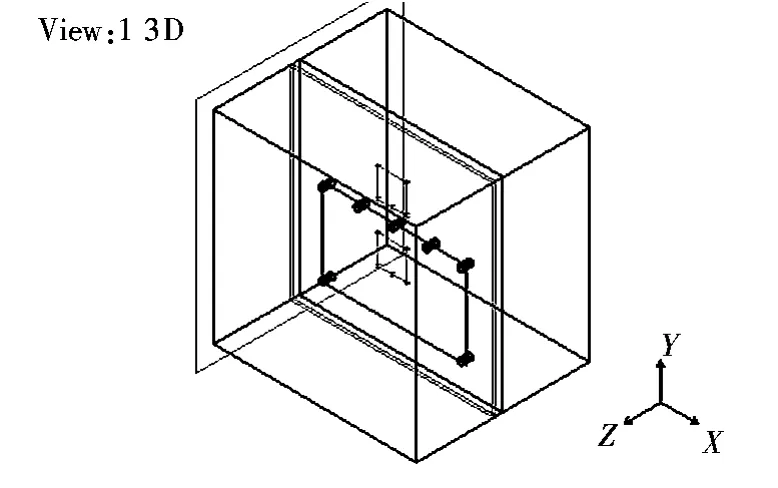
图4 加5个铆钉屏蔽罩Fig.4 The EMC shield with 5 rivets

图5 加5个铆钉屏蔽罩电场强度分布图Fig.5 Distribution charts of the electric field intensity for the EMC shield with 5 rivets
随着优化的继续,陆续出现个别局部最优解,但全局最优解业已出现。图6和图7分别表示当迭代铆钉个数增至24个时的屏蔽罩模型及其对应的电场强度分布情况,将图3、图5、图7的场强分布进行比较,可以看出图7的电磁谐振程度已得到显著降低。为证明图7的电场强度最小,可再继续迭代,图8和图9表示铆钉个数增到26个时的情况。
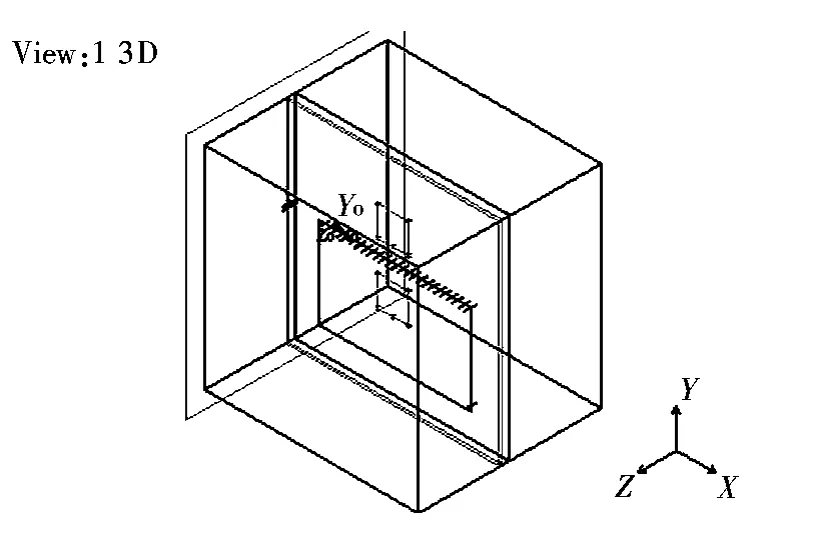
图6 加24个铆钉屏蔽罩Fig.6 The EMC shield with 24 rivets

图7 加24个铆钉屏蔽罩电场强度分布图Fig.7 Distribution charts of the electric field intensity for the EMC shield with 24 rivets
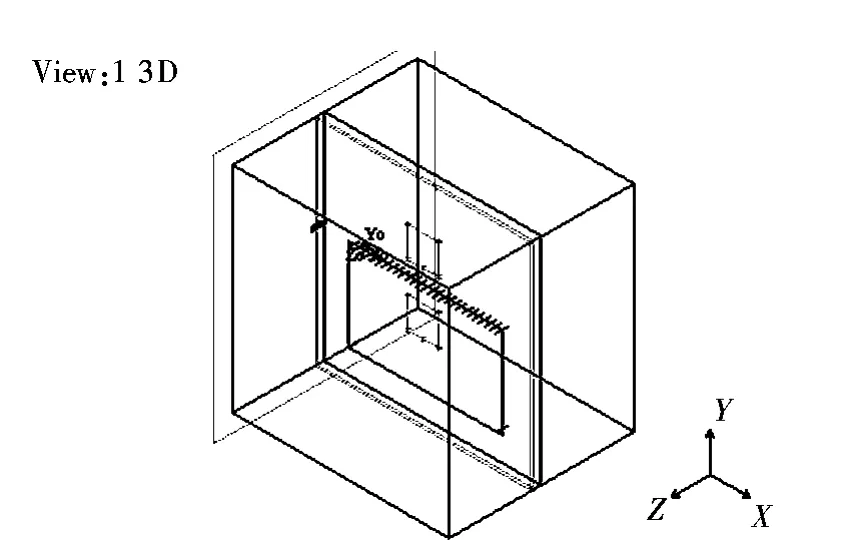
图8 加26个铆钉屏蔽罩Fig.8 The EMC shield with 26 rivets
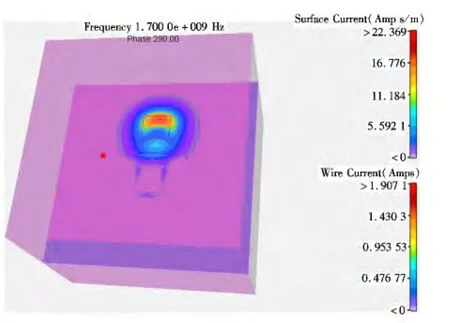
图9 加26个铆钉屏蔽罩电场强度分布图Fig.9 Distribution charts of the electric field intensity for the EMC shield with 26 rivets
为确保全局最优,迭代仍旧继续。
由图7和图9的对比可以看出,24个铆钉屏蔽罩为全局最优解,谐振分布在铆钉接地附近,没有再继续延展,在所有计算结果中,图7电磁发射水平最低,谐振程度基本得到了抑制,射频表面电流降低到低能量区(呈蓝色),图9表明射频表面电流再次形成上升趋势(呈橙色),换言之,再增加铆钉数量对电磁发射水平的控制失去意义,射频接地电流的逐渐增大,产生了耦合效应,射频能量有了新的感应途径,即增加了电磁污染又增大了加工难度[6]。
现将2个铆钉屏蔽罩和24个铆钉屏蔽罩进行实际频谱分析,采用罗德与斯瓦茨ESU系列接收机(Meas.Time 1000 ms;Bandwidth 120 kHz;Frequency 30 MHz-1 GHz,对数坐标)得到的测试结果如图10和图11所示。
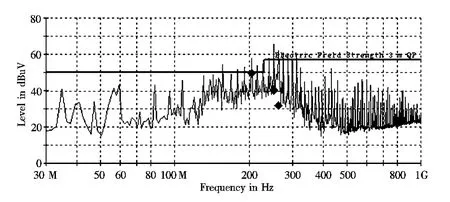
图10 加2个铆钉屏蔽罩实际测试结果图Fig.10 The result of the test for the EMC shield with 2 rivets
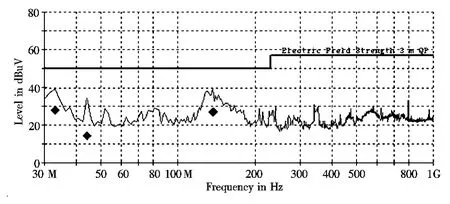
图11 加24个铆钉屏蔽罩实际测试结果图Fig.11 The result of the test for the EMC shield with 24 rivets
现场实际测试效果与仿真结果基本吻合,图10中的谐振频点通过增加铆钉数量在图11中得到了有效的削弱。
由以上数据得出结论,在求解域[2,30]内,24个铆钉为最优解,其场强分布均匀,且值小无畸变,对屏蔽层的穿透能力最小,辐射骚扰最低,在面对诸如5铆钉和26铆钉结构的局部最优解有较高概率的摆脱能力,确保最优结构和最优结果的设计和产生。
3 结束语
本次模拟退火法优化在电磁领域屏蔽隔离中的应用属于探索性的研究,其变量单一且求解域简单。该范例的成功应用,为产品结构参数的电磁优化建立了理论基础,为多变量和复杂问题的求解和优化进行了技术储备,为越来越丰富且针对不同求解问题的优化方法的引入扫清了技术障碍。
[1]陈炜峰,刘伟莲,周香.电磁兼容及其测试技术[J].电子测量技术,2008,31(1):101-104.
[2]蒋龙聪,刘江平.模拟退火算法及其改进[J].工程地球物理学报,2007,4(2):120-126.
[3]马坤,于海平,彭启山.改进的遗传模拟退火算法在TSP中的应用[J].武汉科技大学学报:自然科学版,2006,19(3):210-214.
[4]赵晶,唐焕文,朱训芝.模拟退火算法的一种改进及其应用研究[J].大连理工大学学报,2006,46(5):60-66.
[5]区健昌.电子设备的电磁兼容性设计[M].北京:电子工业出版社,2003:50-55.
[6]陈安伟,陈晓刚,裘愉涛.智能变电站的电磁兼容性测试[J].电力系统自动化,2012,36(12):42-45.
