二维曲线相似与统计学原理在旋转设备故障识别中的应用

2014-11-02李广敏陈江伟纪晓轮张旭野王星星

盐城工学院学报（自然科学版） 2014年3期

李广敏，陈江伟，纪晓轮，张旭野，王星星

(江苏国电南自海吉科技有限公司，江苏南京 210009)

在工业领域中大量使用旋转机械，如风机、水泵、发电机等，这些设备一旦出现故障，往往会造成经济损失甚至安全事故。为防止旋转设备严重故障的发生，工业领域中越来越多的采用状态监测及故障诊断技术［1］。

目前工业诊断中通常采用设置阈值或数值的变化趋势实现故障预警，再通过大量的故障诊断算法实现故障识别。但是不同种类和大小的旋转设备需要研究不同的振动诊断算法，这使得故障诊断的通用性很差，降低了设备故障识别的准确率，往往当确定设备存在故障后，需要通过人力来实现诊断［2］。

通过对旋转设备常见故障的研究发现，相同类型故障的信号频谱之间存在相似性，通过将设备信号的频谱与典型故障频谱进行比对，容易识别出设备的故障类型，并且此工作可由计算机完成。本文主要从数学的角度，借助于统计手段，研究任意曲线几何形态相似性的定义、度量与应用问题。

1 曲线相似性定义与相似度计算

定义:设T为相似阈值，a为两种频谱的相似度，且a和T在0到1闭区间取值，当a＞T时，认为两种故障频谱曲线相似，T为经验值。

设图1曲线为f(x)，图2曲线为g(x)，如果图1与图2曲线几何形态相似，则必满足f(x)=k×g(x)(k＞0)。

图1 f(x)曲线图Fig.1 Curve of f(x)

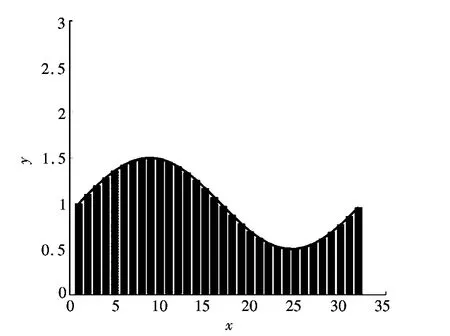
图2 g(x)曲线图Fig.2 Curve of g(x)

可以得出曲线f(x)与g(x)相似的必要条件为:f(x)=k×g(x)(k＞0)。

下面论述f(x)=k×g(x)(k＞0)是曲线f(x)与g(x)相似的充分条件。引用欧几里得几何里关于三角形相似的说法:存在两个三角形，其中一个三角形通过放大或缩小n倍后能够与另外一个三角形完全重合，那么这两个三角形相似。由该定理扩展到曲线相似可得:存在两条曲线f(x)与g(x)，当其中一条曲线经过放大或缩小后能够完全与另外一条曲线重合，那么这两条曲线相似。

f(x)=k×g(x)(k＞0)说明g(x)经过k倍变化后能与f(x)完全重合，所以f(x)=k×g(x)(k＞0)是曲线f(x)与曲线g(x)相似的充分条件。并且定义当曲线f(x)与曲线g(x)相似时，相似度为1。

当f(x)=k×g(x)(k＞0)在x的定义域范围内不能完全成立时，那么曲线f(x)与曲线g(x)不完全相似，引入相似度数学量表示两曲线的相似程度［3］。

由f(x)=k×g(x)得k=f(x)/g(x)

对于定义域范围内的任意x成立，设集合X={x0，x1，x2，x3，…，xn}为 x 在定义域范围内的取样序列，则可得出:

当两曲线不完全相似时此连等式将不成立，由此推导相似度计算方法，图1与图2为两曲线，X轴为频率，Y轴为幅值。将两曲线等间隔的分割，将曲线看成由多个矩形组成，设R1(n)表示图1中自左向右第n个矩形高度，R2(n)表示图2中自左向右第n个矩形高度，两曲线分割的矩形数量相等为 m，设［4］:

几何中三角形相似定理指出，两个三角形对应三条边成比例，即可得出两个三角形相似，由此以曲线被分割的小矩形类比三角形的边给出曲线相似度计算的公式，设:

相似度a=1－［R1(1)/R2(1)+R1(2)/R2(2)+R1(3)/R2(3)+… +R1(m)/R2(m)］/m。通过比较a与T的大小判断两波形是否近似相似［5］。

2 应用算例

图3为函数f(t)=sin(2×pi×15×t)+2×sin(2×pi×40×t)的时域波形和经过FFT变换后频谱波形，图4为函数g(t)=0.8×sin(2×pi×40×t)+0.3×sin(2×pi×15×t)的时域波形和经过FFT变换后的频谱波形，图中采样点m=128，振幅单位为数学约化单位1(下同)。通过函数表达式和频谱图可以定性看出两者是相似的。

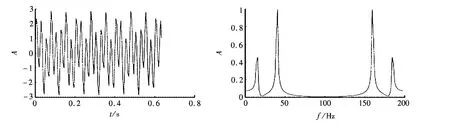
图3 f(t)时域与频域波形Fig.3 f(t)in frequency domain and time domain waveform

设F(f)为f(t)的频谱函数，G(f)为g(t)的频谱函数，f为频率，f在定义域［0，200］内等间隔取样128点，计算可得集合A={F(f0)，F(f1)，F(f2)，…，F(f128)}，B={G(f0)，G(f1)，G(f2)，…，G(f128)}

设 D={A0/B0，A1/B1，A2/B2，…，A128/B128}，则相似度 a=1－sum(D)/128=0.9069。可以说明f(t)与g(t)的频谱有90%的相似度，该计算方法可以很好的给出两曲线相似度的度量方法。

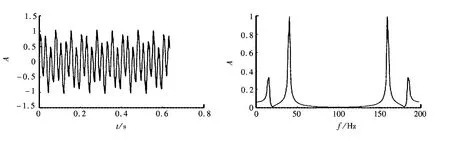
图4 f(x)曲线图Fig.4 g(t)in frequency domain and time domain waveform

图5 k(t)时域与频域波形Fig.5 k(t)in frequency domain and time domain waveform

对f(t)作出修改，使k(t)=2×sin(2×pi×15×t)+1×sin(2×pi×40×t)，图(5)为该函数的时域和频域波形。按以上方法计算修改后的f(t)与g(t)的频谱相似度为0.4200，说明两者相似度很低。通过图(5)与图(4)的对比可以看出两函数在时域与频域上的相似度也是很低的，说明此相似度计算方法可以很好地反应曲线间相似程度。

由计算公式可以看出，两曲线的相似度值受计算时m的取值影响，表1列出m为128、256、512、1024、1536时函数 f(t)=sin(2×pi×15×t)+2×sin(2×pi×40×t)与函数 g(t)=0.8×sin(2×pi×40×t)+0.3×sin(2×pi×15×t)频域的相似度值。

通过对表1数据的分析，m的取值变化对相似度值影响不大，建议工程运用中采用多种m值求相似度平均值的方法。