城市交叉口混合交通流到达模型分析
2014-07-24王春娥王世榉
王春娥,周 磊,王 焱,王世榉
(1.盐城工学院 材料工程学院,江苏 盐城 224051; 2.盐城工学院 电气工程学院,江苏 盐城 224051)
城市交叉口混合交通流到达模型分析
王春娥1,周 磊2,王 焱1,王世榉1
(1.盐城工学院 材料工程学院,江苏 盐城 224051; 2.盐城工学院 电气工程学院,江苏 盐城 224051)
以城市交叉口机动车、电动车、行人为对象,研究混合交通流的到达模型。通过调查获得3种交通流每10 s的到达数据,运用数理方法对其到达特性进行分析。结果表明,机动车的到达特性不一致,电动车、行人的到达特性都符合负二项分布。最后确定3种交通流的到达模型和单位时间内到达交叉口的概率。结果表明,单位时间内交通流到达数越少,概率越大。
交通工程;混合交通流;到达特性;到达模型;到达概率
混合交通流是指机动车、电动车、自行车、行人等交通流在同一道路空间内行驶。在城市交叉口,混合交通流相互交叉,导致交通秩序混乱,交通拥堵与事故频发,通行能力下降等不利影响。
目前对交通流到达模型的研究主要集中于机动车,且相关理论也非常成熟[1-2]。国外对自行车的到达特性进行了研究,认为在自行车流量不大时,泊松分布能较好地描述一定时间间隔内自行车到达量的分布规律[3-4]。国内的彭锐博士对上海4个路口的自行车到达情况进行了分析,认为在流量为2 760~3 720辆/当量小时的情况下,自行车1 min到达量大部分符合负二项分布[5];钱大琳对2个交叉口的自行车流在不同流量时的到达特性进行研究,得出自行车流量每小时在232辆以下时,泊松分布比较适用于描述自行车到达量的统计分布;而当自行车流量很大时(如800辆/h以上),负二项分布比较适合描述自行车到达量的统计分布[6]。由于目前城市道路中自行车数量很少,因此本文只对交叉口机动车、电动车、行人的到达特性进行分析。
1 混合交通流的到达分布模型
概率统计方法是最早应用于交通流理论的数学方法,它为解决交通中具有随机性现象的问题提供了有效手段。
1.1 到达模型的选择
到达规律是交通流运行的基本规律之一。车辆的到达在某些程度上具有随机性,所得的数列可以用离散型分布描述。主要模型有以下3种[1-2]。
1.1.1 泊松分布
(1)基本公式
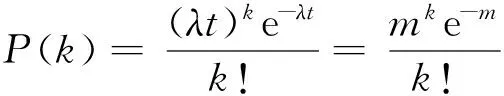
(1)
式中:P(k)为在计数间隔t内到达k辆车的概率;λ为单位时间内的平均到达率;t为每个计数间隔持续的时间;e为自然对数的底,取值为2.718 28。
(2)适用条件
车流密度不大,车辆间相互影响微弱,其他外界干扰因素基本上不存在,即车流是随机的,此时应用泊松分布能较好的拟合观测数据。因此当观测数据m/S2接近于1时,泊松分布适用。
若令m=λt为在计数间隔t内平均到达的车辆,参数m、S2可按下式计算。
(2)
式中:g为观测数据分组数;fj为计算间隔t内到达kj辆车的频数;kj为计数间隔t内到达数;N为观测的总计间隔数。
1.1.2 二项分布
(1)基本公式
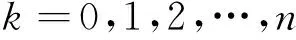
(3)
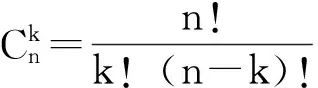
(4)
(2)适用条件
车流比较拥挤、自由行驶机会不多时用二项分布拟合较好。由于二项分布的均值大于方差,所以当观测数据m/S2>1时,二项分布适用。
1.1.3 负二项分布
(1)基本公式
(5)
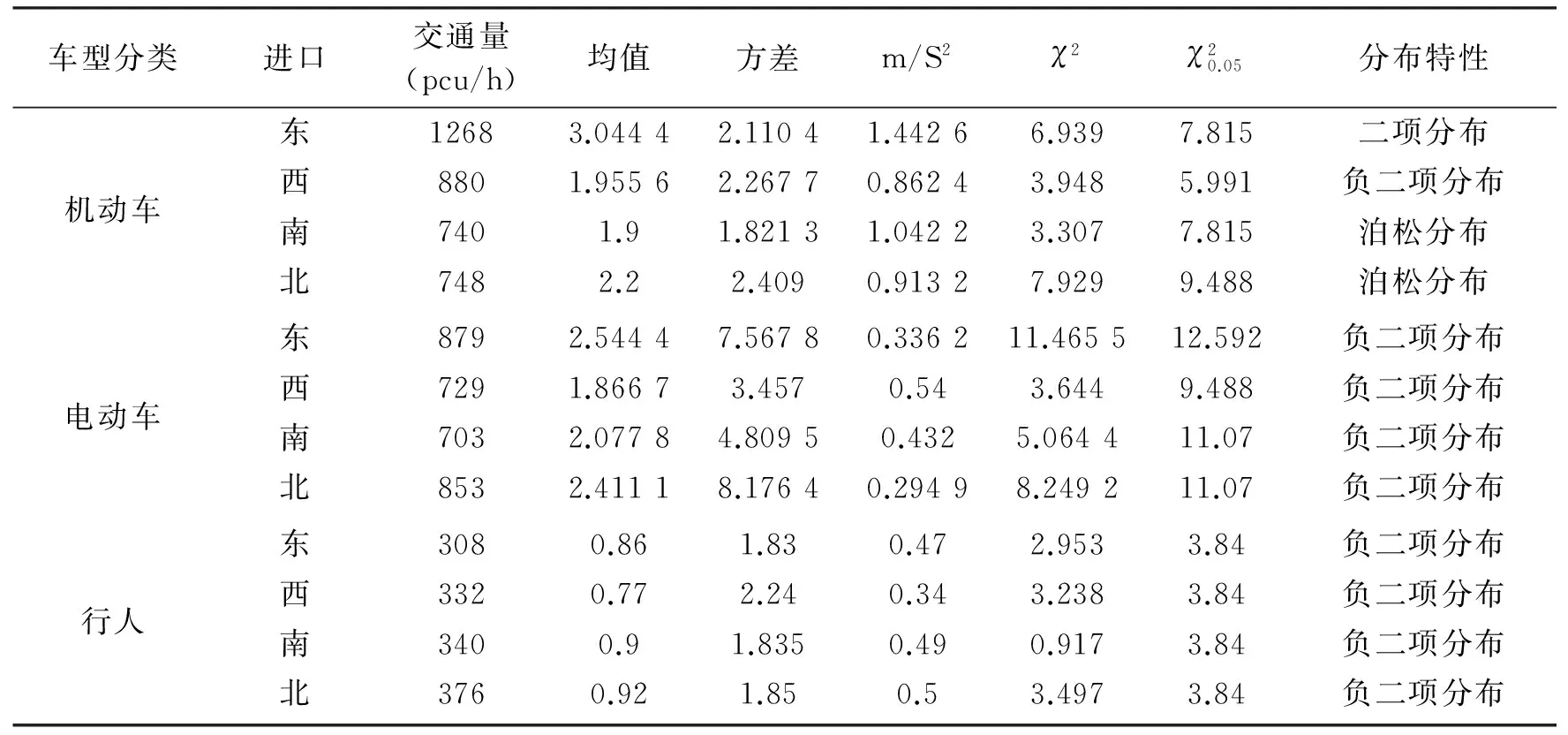
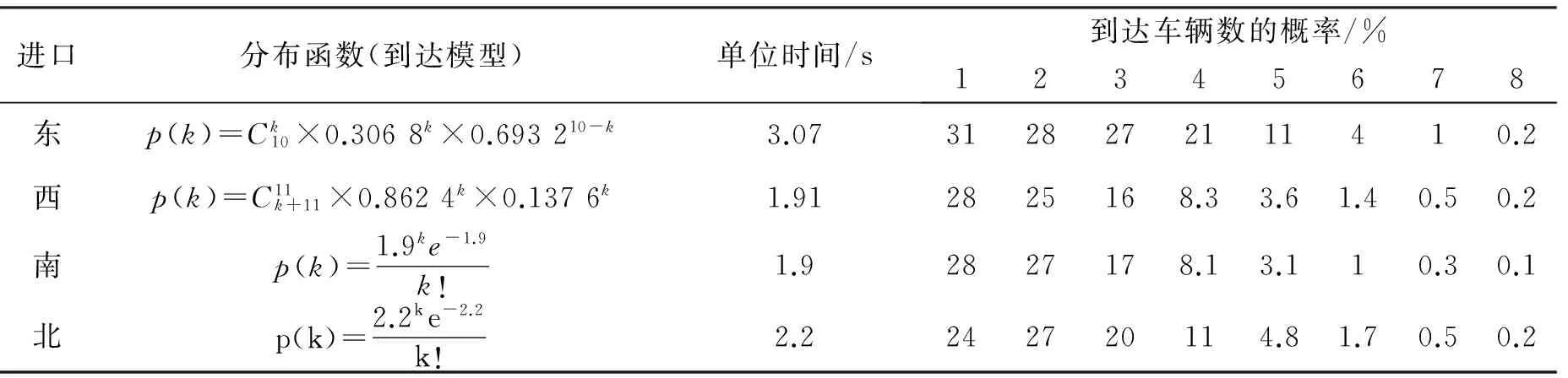
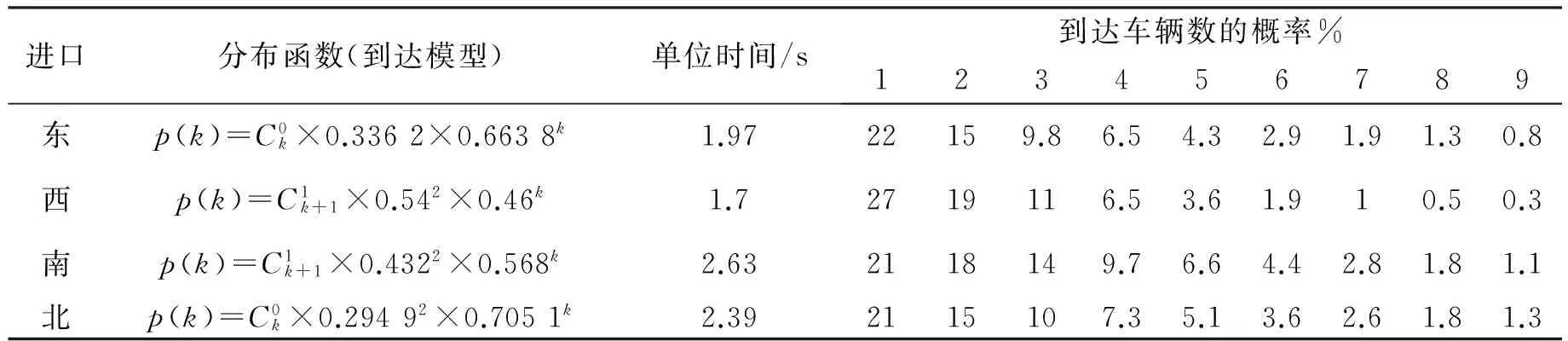
式中p,β为负二项分布参数;0 (6) (2)适用条件 当到达的车流波动性很大时,所得数据可能有较大的方差。当观测数据m/S2<1时,应使用负二项分布拟合观测数据。 1.2 到达模型的验证—χ2检验 进行χ2检验的步骤为: 1.2.1 建立原假设H0 原假设H0是:随机变量X服从某完全给定的概率分布。 1.2.2 选择适宜的统计量 把数据分成g组,fj表示落入第j段的个数(j=1,2,…,g),fj称作频数,fj/n则称频率。假设频率分布在第j段区间上的概率记为pj,Fj=npj称为理论频数。χ2可按下式计算: (7) 1.2.3 确定统计量的临界值 表1 常用离散型分布的DFTable 1 DF of discrete distribution 1.2.4 判定统计检验结果 χ2分布是一种渐近分布,为了正确使用χ2检验法,在应用过程中应注意: (1)总频数n应较大,即样本容量应较大。 (2)分组应连续,分组数g应较大,通常要求g不小于5。 (3)各组内的理论频数Fj=npj不少于5。如果某组内的理论频数Fj<5,则应将相邻若干组合并,直至合并后的理论频数大于5为止,但此时应以合并后的实有组数作为计算χ2自由度的g值。 (4)在交通工程中,通常取α=0.05。 2.1 调查方案及数据处理 本文调查对象为盐城市建军路-文港路交叉口。建军路是东西主干道,西边是盐城老城区,人口密集、商业繁华,东边是亭湖新区,有大量的工厂;文港路是南北干道,周围有学校、小区等人流集中地,附近有火车站、汽车站等交通吸引点,因此该交叉口是进出盐城老城区的枢纽,并且大型客货车比重很大,交通流比较复杂。 调查时段选取工作日高峰时段的11:00-12:00。因为在高峰时段,交通流更复杂,交通秩序更混乱。调查采用人工计数法,分东、西、南、北4个进口对机动车、电动车、行人每10 s的到达情况进行统计,其中机动车分大型、中型、小型3种车型分别记录,然后换算为标准小汽车。 根据上面的分析过程,对该交叉口混合车流的到达特性进行分析,得到表2。 由表2可知,在该时段机动车的到达特性不一致;其中,东进口交通量非常大,使得数据的均值大于方差,到达特性符合二项分布;西进口为从市区驶出的车流,车流波动性大,因此数据的方差较大,车流符合负二项分布;南、北进口交通量不大,车流的到达是随机的,车流到达符合泊松分布。此外,机动车的到达特性还与交叉口的渠化情况有关。当交通量相同时,进口车道数越多,车流之间的干扰相对较少,机动车越趋向于泊松分布。因此,当交通量少、交叉口车道数多时,机动车趋向于符合泊松分布;交通量多、交叉口车道数少时,机动车趋向于符合负二项分布或二项分布。 表2 交叉口混合车流的到达特性分析表Table 2 The arrival characteristic of mixed-traffic flow in intersection 由于车型小、机动灵活、信号控制等因素,电动车在交叉口的速度差别较大,造成数据的方差远大于均值,故该交叉口电动车的到达特性都符合负二项分布。行人的到达也都符合负二项分布,原因是行人数量比较小,且到达比较分散,导致m/S2<1。 2.2 到达模型的确定及应用 根据表2的数据可确定出交叉口机动车、电动车和行人的到达模型。根据概率分布函数,可预测出3种交通流在单位时间内的到达概率,分别如表3~表5所示。表3中,东进口一行的数据表示根据概率分布函数计算出在单位时间3.07 s内机动车分别到达1~8辆的概率。 由表3可知,因为机动车的到达特性不一致,由此得出的到达模型差别较大。在单位时间内,东进口到达机动车数概率较大的为1~4辆,超过8辆的概率为0;其他进口到达机动车数概率较大的为1~3辆。 由表4、表5可知,由于电动车、行人的到达特性一致,由此得出的到达模型和概率值差别不大。在单位时间内,到达电动车数概率较大的为1~3辆,行人到达数概率较大的为1~2人。 表3 机动车到达模型及概率表Table 3 The arrival model and probability of motor vehicle 表4 电动车到达模型及概率表Table 4 The arrival model and probability of electric bicycle 表5 行人到达模型及概率表Table 5 The arrival model and probability of pedestrian 通过调查和数据分析,得到交叉口机动车、电动车、行人的到达特性,然后确定其到达模型,主要结论为: (1)受交叉口渠化情况、交通量大小、到达随机性等因素的影响,交叉口各个进口机动车的到达特性不完全一致。当交通量少、交叉口车道数多时,机动车之间的干扰较少,车辆到达趋向于符合泊松分布;车流的到达波动性较大时,趋向于符合负二项分布;交通量多、交叉口车道数少时,趋向于符合二项分布。 (2)当交叉口非机动车道、人行道宽度一定时,电动车、行人的到达特性比较一致。 (3)利用数理方法和调查的数据,分别确定3种交通流在交叉口各个进口方向的分布函数,并预测了3种交通流在单位时间内的到达概率。结果表明,单位时间内到达数越少,概率越大。 由于数据有限,本文得出的结论有一定的局限性,要得到成熟的模型需要对大量的交叉口进行广泛的数据调研,这将是以后的工作内容。 [1] 徐吉谦,陈学武.交通工程总论[M].北京:人民交通出版社,2008. [2] 王炜,过秀成.交通工程学[M].南京:东南大学出版社,2009. [3] Faghri,Egyhaziova. Development of a computer simulation Model of Mixed Motor Vehicle and Bicycle Traffic on Urban Road Network[J].Transportation Research Record, 1999, 1674: 86-93. [4] Southwest Region University Transportation Center. Behavioral Models and Characteristics of Bicycle-Automobile Mixed-Traffic:Planning and Engineering Implications, SWUTC/98/60056-1[R]. Texas:Center for Transportation Research, 1998. [5] 彭锐.自行车交通流理论[D].上海:同济大学,1993. [6] 钱大琳,黄迪,赵春龙,等.中国特大城市自行车到达的统计分布研究[J].数学的实践与认识,2005,35(9):67-70. (责任编辑:李华云) Analysis of Arrival Model of Mixed-Traffic Flow in Urban Intersection WANG Chune1, ZHOU Lei2, WANG Yan1, WANG Shiju1 1.School of Material Engineering, Yancheng Institute of Technology, Yancheng Jiangsu 224051,China;2.School of Electrical Engineering, Yancheng Institute of Technology, Yancheng Jiangsu 224051, China In order to study the arrival model of mixed-traffic flow in urban intersection,the paper put motor vehicles, electric bicycles and pedestrians as the research object. Firstly the arrival data in every 10 s could be got through the survey. Then the arrival characteristics of motor vehicle, electric bicycle and pedestrians were analyzed using the mathematical method. The results show that the arrival characteristics of motor vehicle in each intersection entrance are inconformity; the arrival characteristics of electric bicycle and pedestrians all conform to negative binomial distribution. Finally, the arrival models of motor vehicles, electric bicycles and pedestrians were determined and the smaller arrival probability in a unit time were predicted. The results show that the arrival number in unit time, the greater probability. traffic engineering; mixed-traffic flow; arrival characteristic; arrival model; arrival probability 2014-02-24 王春娥(1983-),女,山东潍坊人,讲师,硕士,主要研究方向为交通设施设置、交通流理论及交通控制理论与方法。 U491.4 A 1671-5322(2014)03-0075-04

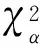
2 实例验证

3 结论
