高职院校高等数学与专业课教学相融合的探讨

陶华

(江苏建筑职业技术学院 基础部,江苏 徐州 221008)

高职院校高等数学与专业课教学相融合的探讨

陶华

(江苏建筑职业技术学院 基础部,江苏 徐州 221008)

高职院校高等数学应当遵循“以应用为目的,以必须、够用为度”的原则,实现与专业课教学的融合,充分发挥数学思维方法在解决专业问题中的作用,不断提高学生分析和解决实际问题的能力.对高等数学与专业课教学相融合的途径进行了分析,并通过教学实例探讨了数学方法在相关专业教学中的应用.

高职院校;高等数学;专业;教学;融合

高等数学是高职院校各专业重要的基础课程.该课程不仅是讲授数学知识,更重要的是传授高等数学的思想、文化、工具和方法.高等数学对于培养学生最基本的科学文化素养具有不可替代的作用,其实质在于只有使学生理解并掌握了高等数学博大精深的思想和文化,才能真正提高其逻辑思维能力、分析问题和解决实际问题的能力,进而得心应手地应用其思想、工具和方法处理生产实践中的相关技术难题[1-2].因此,在高等数学教学中,特别是在现今专业课实践环节增多,基础课学时有所减少的情况下,如何将高等数学与专业课教学相融合,使教学内容与生产实际有机融合,达到高数课程学时虽有所减少,而学生的应用能力不会随之削弱的效果,是十分值得探讨的问题.

本文拟以上述考虑为前提,分析高等数学与高职专业教学相融合的途径,并以教学实例探讨教学方法在相关专业教学中的应用.

1 高职高等数学与专业课教学相融合的途径

高等数学作为高职教育的一门公共基础课程,承担着为学生提供学习后续课程和解决实际问题的数学基础与方法的重任,对高职专业教育的成效起着至关重要的作用.在教学改革加强专业实践环节,基础课学时相对减少的态势下,高等数学亟待从传统的教学模式中走出来,寻找新的、与之相适合的教学模式.从目前来看,高职高等数学的教学模式基本是班级集中式授课,不论何种专业,学生学习的只是抽象的概念和公式,与所学专业毫无关联,学生在学习中看不到所需,找不到方向,因而失去了学习的动力和热情.因此,笔者认为高等数学必须坚持教学改革方向,在课程教学中着力突出基本概念的清晰性和准确性,突出基本理论的应用,以及突出用基本方法解决生产实际问题[1],积极探索与专业教学相融合的有效途径.

首先,可根据专业的多样性设置模块教学.即根据不同专业的教学要求,将高等数学教学内容分为公共模块、专业模块和选学模块三部分[3].公共模块为各类专业的必学内容,包括一元函数微积分、数学实验等.专业模块根据不同专业的拓展而设置,包括二元函数微积分、线性代数及应用、概率统计初步、数学建模案例等.专业模块也是重点模块,内容可由各专业教师和数学教师共同研讨确定,以解决与专业相关的实际问题为重点,突出一个“用”字.如对于电信系学生而言,专业学习和实践需用到线性代数知识,在专业模块中即安排这部分的学习内容;而对于经管系学生,其业务实践多用到概率知识,在专业模块中则安排与之相应的内容.因此,不同的专业选择不同的专业模块,应充分体现高职数学课程大纲所要求的“以应用为目的,以必须、够用为度”的教学原则,使学生能更有针对性地学习.选学模块依据各模块教学要求以及生源构成,使内容深度呈现层次性变化,也可适当安排一些数学史及趣味数学等,用以培养学生对数学的兴趣.

其次,在课堂教学中,应将数学建模、数学实验的思想与方法融入高等数学课程中,着重培养学生分析、解决问题的能力.要通过引入不同情景模型案例教学,以专业应用案例为载体,将数学教学与专业学习紧密结合,并通过对一些经典的模型进行分析、讲解、练习,使学生学会将实际问题转化为数学问题,进行分析后予以解决.

其三,将考核方式与专业相融合.要改变以往单纯的考核方式,努力实现多元化考核.以往高数考核一般为平时成绩+期末成绩=总成绩,即囿于“平时看出勤,期末一张卷”的传统模式.为突破单纯考核模式,更好地开展和检验高等数学与专业的融合,可以将学生解决专业课中数学问题的能力纳入考核范围,列为实践成绩,使之参与构成学生期末总成绩,以鼓励和促进学生变被动学习为主动学习,不断提高对高等数学的学习热情.

2 高职高等数学与专业课教学相融合的实例

下面以定积分的学习探讨数学方法在对相关专业教学中的应用.定积分是高等数学理论体系的重要构架之一,其解决问题的思想方法对于生产实践具有重要的指导作用[4].在解决实际问题中,微元法作为是一种有效的方法,广泛应用于解决流体力学、应用力学、热学、电学等实际问题中 .通过对微元法运用的熟练程度,可考察学生分析问题、解决问题的能力[5].为探讨高数理论知识与专业知识的深度融合,笔者以在热环系和经管系教学中的应用实例进行阐述.

2.1 微元法在流体力学中的应用实例

1)背景知识：堰塞湖指地震后引起的大规模山体滑坡,河水冲击泥土、山石而造成堆积,堵截河谷或河床后贮水而形成的湖泊.四川汶川强震造成山区土石大量崩塌,形成多处堰塞湖.图1是卫星二号在2008年5月14日和5月18日航拍所得到的图像.专家们预测：堰塞湖如果崩塌,一夕间即会毁村灭镇.

专家们的预测并非耸人听闻,而是实实在在的重大隐患.这是因为随着堰塞湖水面不断增高,堰塞湖堤坝所受的压力越来越大,当压力超过其所能承受的压力时,堰塞湖堤坝就会崩塌.显然,解决隐患的关键在于密切观测和竭力缓解堰塞湖堤坝承受的压力.那么,如何观测计算堰塞湖堤坝所承受的压力?这个问题实际上就是数学上的液体压力问题.根据观测结果,可用微元法进行计算.

2)剖析：堰塞湖堤坝所受压力相当于将形似堰塞湖横截面的一个薄板斜插入水中所受的水压力.薄板倾角即堤坝与水平面的夹角.该问题可抽象为如下数学问题进行求解.

将边长为a和b的矩形薄板与液面成α角斜沉于液面,位于深h处,设a＞b,液体的比重为Y,求薄板受的液体静压力.

3)解：建立坐标系如图2所示.

图2 矩形薄板所承受的静压力Fig.2 Static pressure on rectangle sheet

薄板一长边的深度为h,另一长边的深度为h+b sinα.用微元法在[h,h+b sin a]中任取[x,x+d x],相应的微元(薄板上阴影部分小横条)长a,宽于是所受压力为

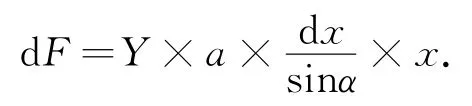
整块板所受静压力为

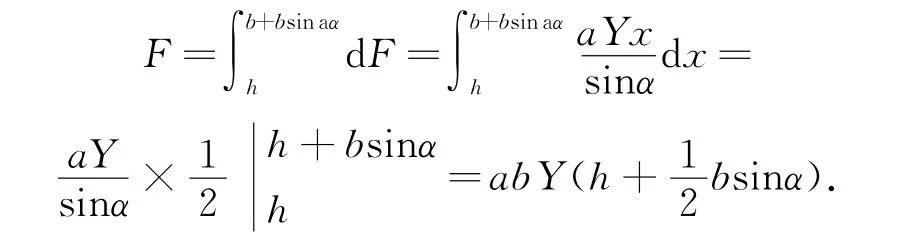
由以上结果可看出,薄板所受静压力与薄板长、宽及所处水深有关.薄板面积越大、所处水深越深,静压力越大.同样,对于堰塞湖堤坝,随着水位的升高、水面的变宽,堤坝所受压力变大,决堤的可能性即变大.

2.2 微元法在经济管理中的应用实例

1)问题：设某产品的总成本C(单位：万元)的变化率是产量x(单位：台)的函数总收益R(单位：万元)的变化率是产量x的函数R′(x)=8-x.

(1)求产量由100台增加到500台时总成本与总收益各增加多少;(2)求产量为多少时,总利润L最大;(3)已知固定成本C(0)=1(万元),分别求出总成本、总利润与总产量的函数关系式;(4)求总利润最大时的总利润、总成本与总收益.

2)解：(1)产量由100台增加到500台时总成本与总收益分别为

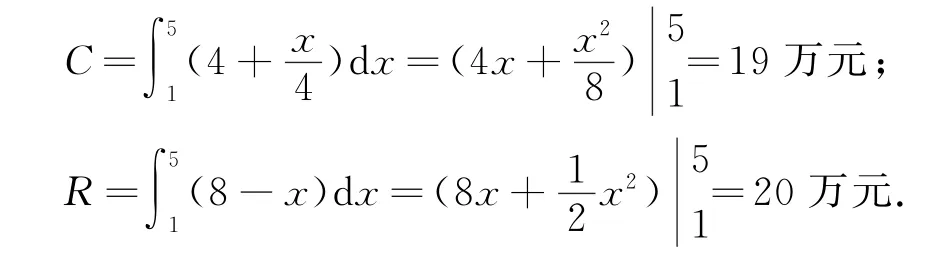
(2)由于总利润L(x)=R(x)-C(x),故

(3)因总成本是固定成本与可变成本之和,故

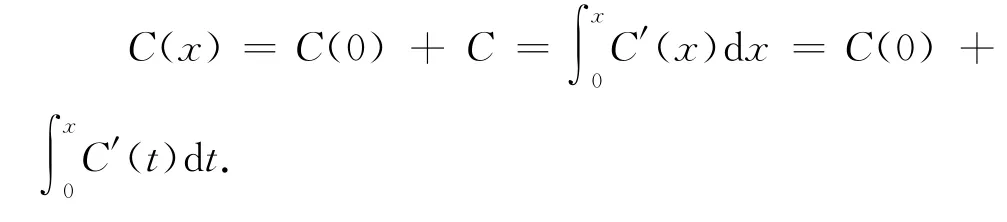
则总成本函数为

3 结语

实践证明,在高等数学的教学中以实际问题为载体,把问题逐层展开,将数学基础知识与专业知识相互融合,使学生感到学有所用,有利于激发学生对高数的学习兴趣,进而调动其课堂学习的积极性和主动性,提高课堂教学效率.这种与专业课相融合的教学方式深受学生的欢迎.高等数学与专业课教学相融合,并不在于讲授多少定理和公式,而在于以“用”为主,密切联系相关专业的实际问题.将高数蕴含的数学思维方法传授给学生,不断提高学生分析问题、解决问题的能力,使高等数学课程真正服务于专业课程,既是高职院校高等数学教学应该达到的目的,也是高职数学教学与专业课教学相融合的应有之义.

[1] 刘家春.高职教育应突出三基在解决生产实际问题中的应用[J].江苏建筑职业技术学院学报,2012,12(4)：44-47.

[2] 张福珍,姜咏梅.民办高职院校高等数学教材改革探索[J].江苏建筑职业技术学院学报,2013,13(2)：40-42.

[3] 高明海,王宝乾,靖晓英.高等数学模块教学模式的探索与构建[J].内蒙古师范大学学报：教育科学版,2006,19(9)：102-104.

[4] 阎章杭.高等数学与工程数学[M].第2版.北京：化学工业出版社,2003.

[5] 陶华.微元法及其应用探讨[J].常州信息职业技术学院学报,2008,7(6)：49-51.

Integration of advanced mathematics and specialized course teaching in higher vocational colleges

TAO Hua
(Department of Basic Education,Jiangsu Jianzhu Institute,Xuzhou,Jiangsu 221116,China)

Advanced mathematics teaching in higher vocational colleges should follow the principles that the purpose is application and the limit is necessity and sufficiency.Through integration of advanced mathematics and specialized course teaching,we should give full play to mathematical thinking method in solving specialized problems and continually improve students'ability to analyze and solve practical problems.This paper analyzes the paths of integration of advanced mathematics and specialized course teaching and discusses application of mathematical methods in relevant specialized course teaching.

higher vocational colleges;advanced mathematics;specialty;teaching;integration

G 640

A

2095-3550(2014)01-0047-03

2013-11-28

院级教研课题：以专业群为目标的高等数学教学培养模式的研究 (2012-19)

陶华,女,江苏徐州人,副教授,硕士.

E-mail：469534365@qq.com

(责任编辑：赵国淮)