正交长迹线裂隙岩体REV存在性与裂隙平均间距探讨

2014-10-27张辛宋宏伟于青春

江苏建筑职业技术学院学报 2014年1期

张辛,宋宏伟,于青春

(1.中国矿业大学深部岩土力学与地下工程国家重点实验室,江苏徐州 221116;2.江苏建筑职业技术学院经济管理与人文学院,江苏徐州 221116;3.中国矿业大学力学与建筑工程学院,江苏徐州 221116;4.中国地质大学水资源与环境学院,北京 100083)

张辛1,2,宋宏伟1,3,于青春4

裂隙岩体表征单元体的大小是岩体水力学特征的尺度效应的客观反映,表征单元体的性质也决定了岩体水力学参数选取的合理性和可靠性.在以理论推导和多元线性回归分析方法验证Fracture-ToKarst软件可靠性的基础上,讨论了正交长迹线裂隙岩体表征单元体的存在性与裂隙平均间距之间的关系,以及表征单元体的合理尺寸,并利用统计学方法求解了表征单元体的渗透系数张量.

裂隙岩体;正交长迹线;表征单元体;渗透系数;平均间距

在水利工程、石油工程、高放射性核废料地下贮存等领域,水文地质参数的选取具有至关重要的作用.其中裂隙岩体渗透系数是最重要的参数之一.岩体与岩块的不同在于其受结构面切割,是具有特定结构的多裂隙体[1].在一般情况下,裂隙的导水性远强于岩块.因此,裂隙结构面的空间分布及自然特性在很大程度上决定着地下水在岩体内的运动规律和透水性质.通过对结构面的产状、间距、分布类型和裂隙张开度等几何特征的研究,可以间接地掌握裂隙岩体地下水渗透的基本规律.多裂隙体的渗流问题一直是地下水科学研究的重点和难点.目前采用的办法多是将裂隙体等效成多孔介质模型,即将非连续问题在一定程度上等效成连续介质问题处理.Witherspoon提出了裂隙岩体渗流的尺寸效应并讨论了裂隙粗糙度对渗透性的影响[2].“尺寸”问题的本质即表征单元体(以下简称REV)的问题,REV概念(即指可以宏观反映研究区域渗透特性的最小区域)最早由Bear提出[3],并证明了二维条件下方向渗透系数与极坐标下与椭圆的关系,即当Kp为流线方向渗透系数时,若使极半径,在极坐标作圆,将成为一个椭球(二维条件为椭圆).Long等人随后提出了裂隙介质可以等效多孔介质的2个基本条件[4].JohanÖhmam和Auli Niemi对等效介质作了大量研究[5-6],为比较方向等效渗透系数与椭圆的相似程度,基于最小二乘法原理提出了判断渗透椭圆相似性的指标RMS,并指出当其不超过0.2时,多孔介质模型可以较好地等效裂隙介质.

近年来国内外有很多学者采用数值模拟方法研究裂隙岩体的渗流问题[79].为了解不同裂隙间距对岩体REV的影响,根据国际岩石力学协会对岩石裂隙的建议分类,本文利用Fracture To Karst软件,讨论了正交长迹线裂隙岩体REV的存在性与裂隙平均间距的关系.此前,张莉丽、张辛等人已论证迹线长度更短时(小于10 m)裂隙模型在20、60、200 mm裂隙间距时肯定有REV的存在[1013],且由于裂隙迹线长度的增加,长迹线的裂隙模型在平均间距小于600 mm时REV均有存在.因此,本文中的裂隙模型间距从大于600 mm开始计算.

1 裂隙岩体的渗透系数张量

裂隙岩体的渗透张量是建立在单一裂隙水流运动规律基础上的.当水流服从达西定律,等宽,两壁光滑的裂隙中流体的平均速度计算公式为

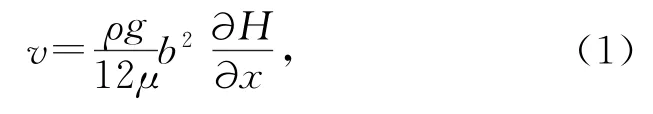
式中：v为平均速度,m/s;ρ为流体密度,kg/m3;μ为动力粘滞系数,kg·m/s;g为重力加速度,m/s2;b为裂隙宽度,m;为x方向上的水头梯度.

如果将裂隙岩体等效成多孔介质模型,即假想流体充满整个岩体流动(流体的流动速度称当量渗透速度),裂隙分布均匀,且裂隙面与水力梯度平行,若有一组符合上述假定的裂隙(如图1所示),则其当量渗透速度为

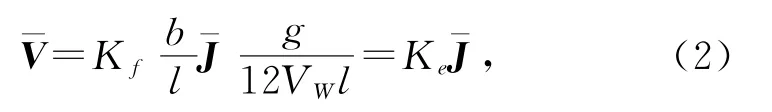
式中：¯V为当量渗透速度,m/s;Kf为单裂隙渗透系数,m/s;Ke为裂隙组的当量渗透系数,m/s;l为裂隙的平均间距,m;¯J为水力梯度;VW为水的运动粘滞系数,m/s2.若图1中裂隙模型裂隙间距为1 m,隙宽为8 mm,水力梯度为0.1,通过式(2)计算得到当量渗透系数=0.418 33 m/s,利用FractrueTo Karst计算得到的当量渗透系数亦为0.418 33 m/s.

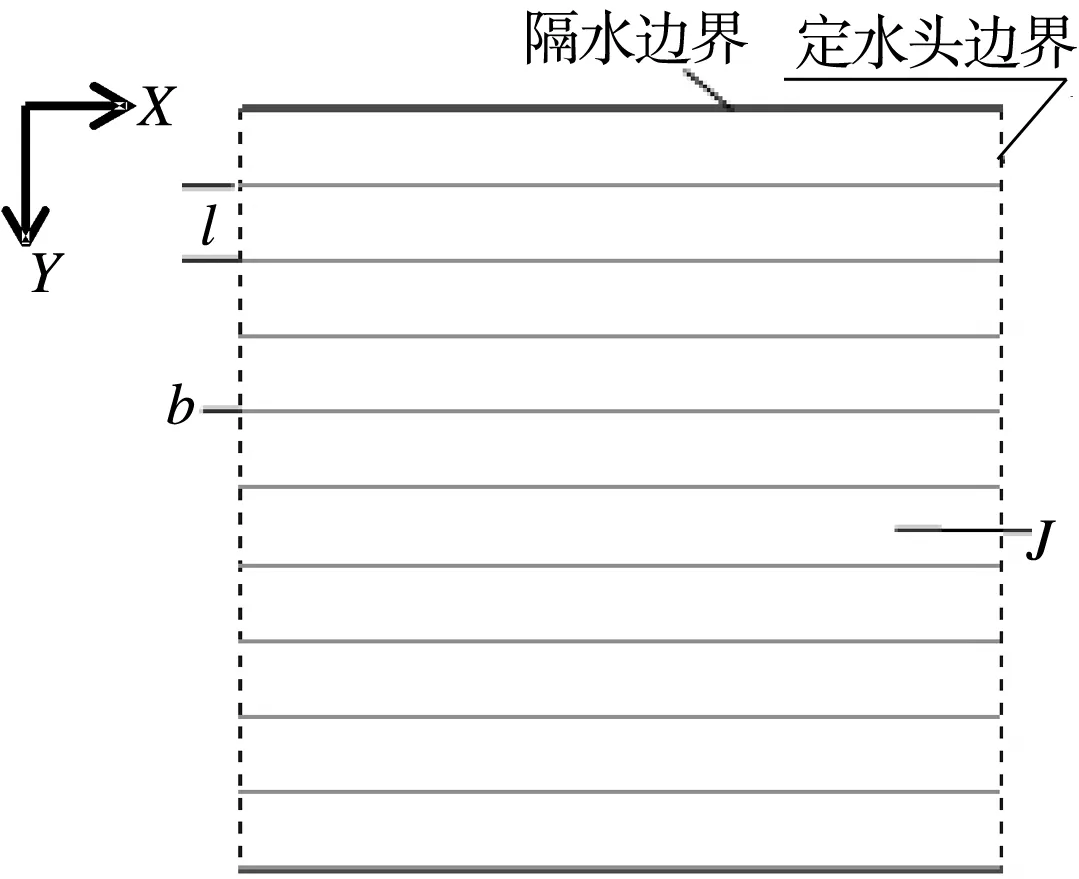
图1 水力梯度与裂隙面平行渗透示意Fig.1 Schematic diagram of hydraulic gradient and parallel permeate of fissure surface

由于水力梯度往往与裂隙面不平行,而水流速度与平行于裂隙面的水力梯度有关,因此水力梯度可以分解为平行裂隙面方向和垂直方向两个矢量,它们之间的关系表达式为

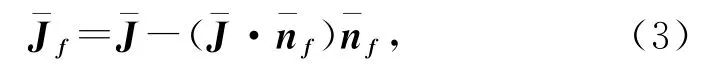
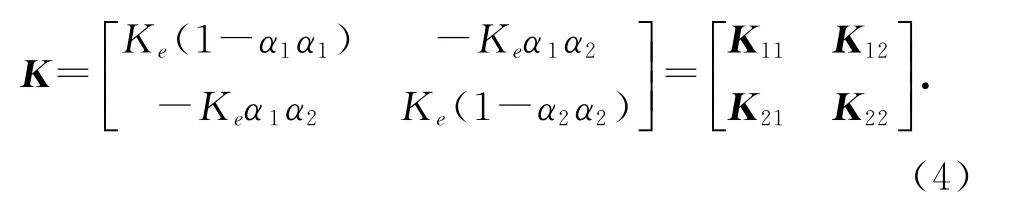
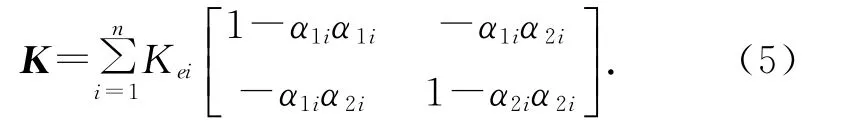
若在图1所示裂隙模型基础上增加一组相同间距及相同隙宽的垂直裂隙,则根据式(5)可求得此裂隙介质的渗透系数张量 K=.利用Fractrue To Karst求得的方向渗透等效系数见表1.

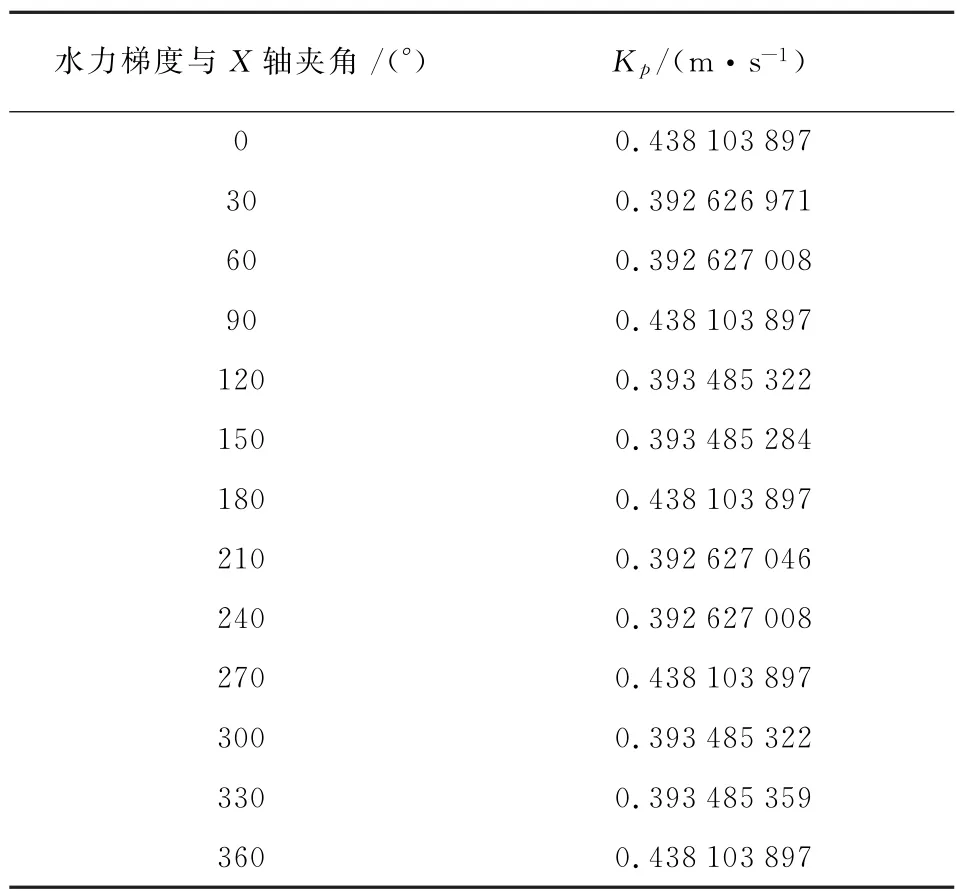
表1 方向等效渗透系数Tab.1 Permeable coefficient of equivalent direction

利用多元线性回归分析方法[14],通过方向等效渗透系数可求解出裂隙介质渗透张量.方向渗透系数Kp(m)可以写作方向矩阵与渗透系数张量相乘的形式：

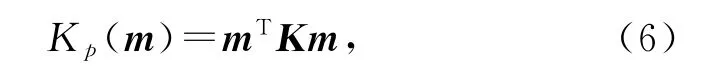
式中：K为裂隙介质的渗透系数张量,m/s;m为方向向量.

如果相互独立的方向渗透系数N≥3,则N个含有K11、K22、K123个未知变量的线性代数方程组,可写作矩阵的形式：

其中：

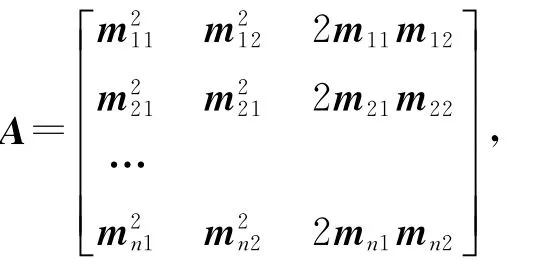
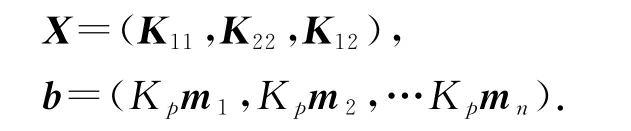
通过多元线性回归分析模型,利用最小二乘法原理即可求得回归系数为K11、K22、K12的裂隙介质模型.利用回归分析方法可以求得其渗透系数张量为,该结果与根据理论计算出的结果比较接近.因此,可认为通过Fracture-To Karst计算的等效渗透系数是可靠的.

2 正交长迹线裂隙模拟

根据1978年国际岩石力学协会的分类表,长迹线裂隙是指裂隙最大迹长大于10 m、小于20 m的裂隙.根据裂隙间距分类表,间距在0.6～2 m间的裂隙为宽间距.由于REV的存在性随间距的增加而减小,如果在间距2 m时REV存在,则在更密的间距也存在.因此,可在80 m×80 m范围内生成2组正交裂隙(隙宽均为0.000 1 m,平均间距为2 m),2组裂隙的参数见表2.共生成裂隙384条,其中水平裂隙192条,垂直裂隙192条.生成的裂隙如图2所示.

图2 模拟裂隙及研究区域示意Fig.2 Schematic diagram of simulated fractures and study area

根据以往的经验,研究图2随机裂隙模型渗透性质的均匀性,只要在研究区域内的各方向渗透系数不随着区域小的变化而剧烈变化,即可确定该模型区域为均匀介质(这也是Long提出的REV存在的第一条件).为此,我们在图2中设计了A、B、C、D 4个研究区域,并保持每个区域的水力梯度均为1.经过数值计算,可以得到每个区域各方向的等效渗透系数.经过渗透系数比较(如图3所示),可以看出从20 m×10 m～30 m×15 m渗透系数发生剧烈变化,而比较30 m×15 m、40 m×20 m、60 m×30 m研究区域,其边界增大时渗透系数并未发生突变.

可见,研究区域大于30 m×15 m时裂隙模型表现出较好的均匀特性,可将其视为最小的均匀尺度.

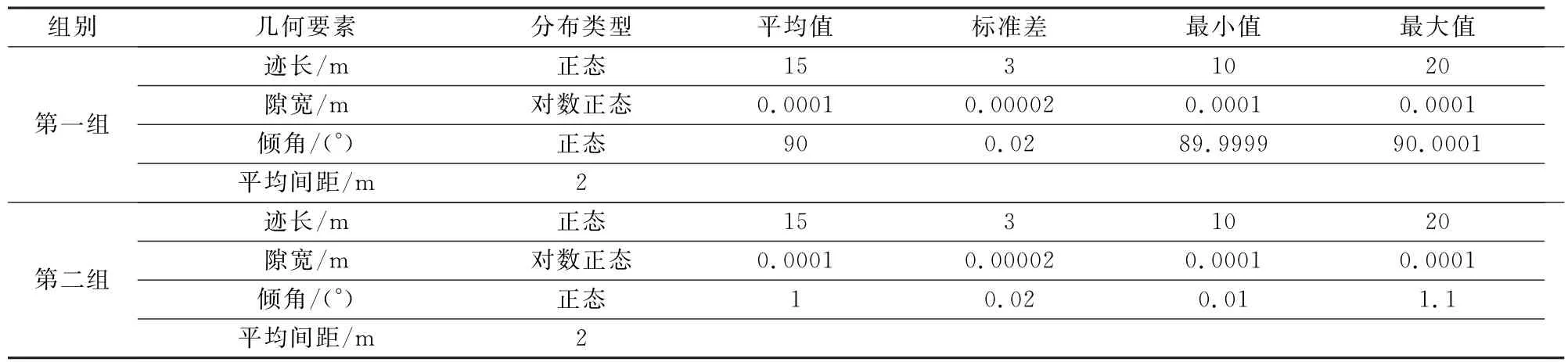
表2 宽间距模拟裂隙几何要素设计值Tab.2 Design value of geometric element of simulated fractures with wide spacing

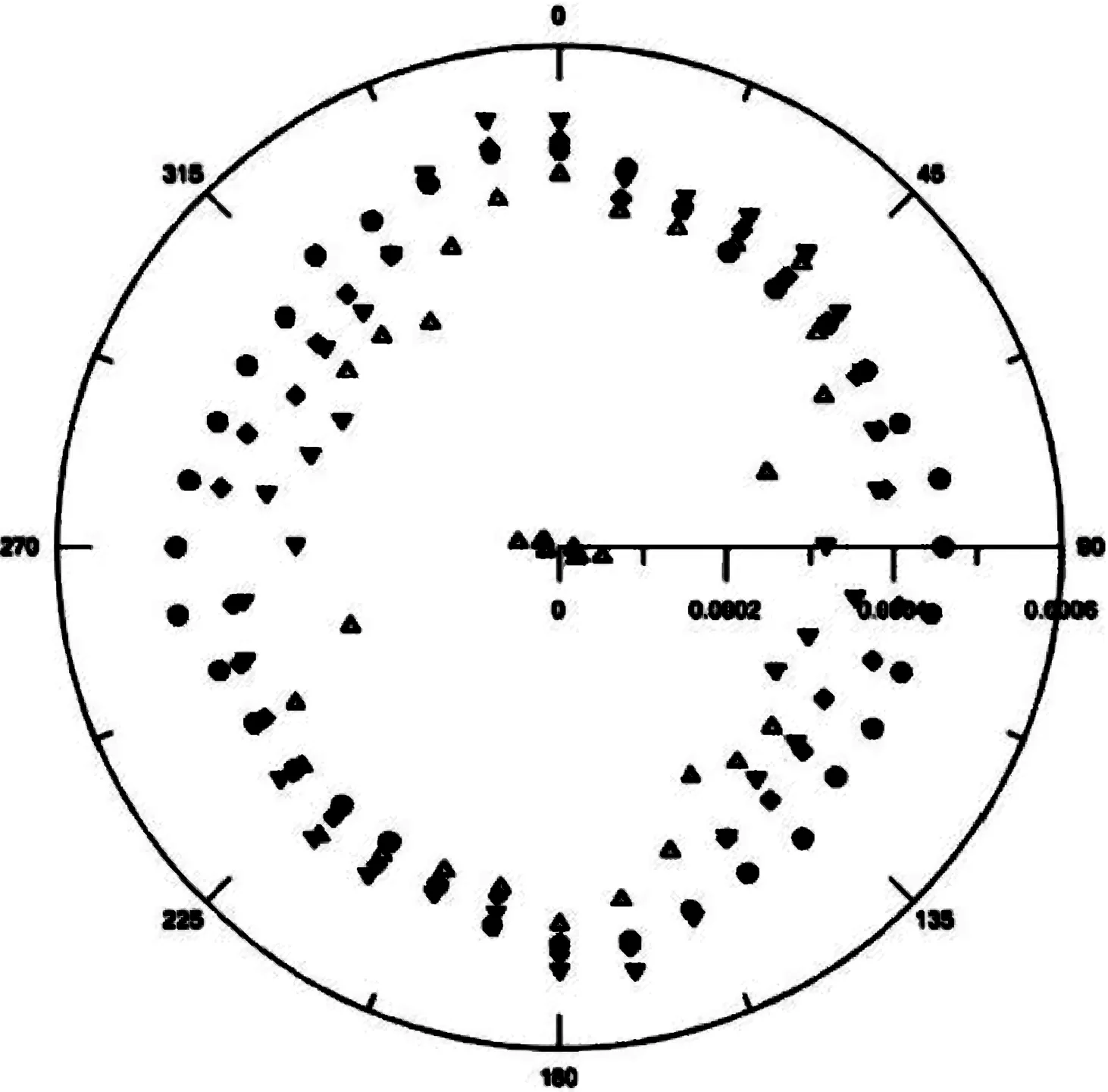
图3 4个区域的方向渗透系数比较Fig.3 Comparison of direction permeable coefficient of 4 study areas

3 方向渗透系数计算与REV的确定

在求得最小均匀区域的基础上,当隔水边界长度大于2倍的透水边界时所得到的等效渗透系数为流线方向渗透系数[13],以流线方向与X轴方向夹角0°为初始角,顺时针旋转,每间隔10°,计算一个等效渗透系数,这样即可得到36个方向的渗透系数.利用极坐标下的椭圆方程[12]对方向渗透系数进行拟合,可以得到拟合曲线(如图4所示),评价拟合度系数RMS为0.20.由此可知,对于该类裂隙岩体模型,当区域大于30 m×15 m时,适宜于用多孔介质等效,其水力学行为也适宜用连续介质模型表示,该区域大小即可视作此类裂隙岩体的REV.根据多元线性回归分析,可得到此裂隙岩体的渗透系数张量

用同样方法计算长迹线裂隙平均间距(4 m和6 m)时发现,当平均间距等于4 m时REV存在且小于100 m×50 m;当裂隙间距为等于6 m时,裂隙在研究区域内无法相互连接构成导水系统,因此REV可能不存在.可以得到的正交长迹线裂隙岩体REV存在的情况见表3.

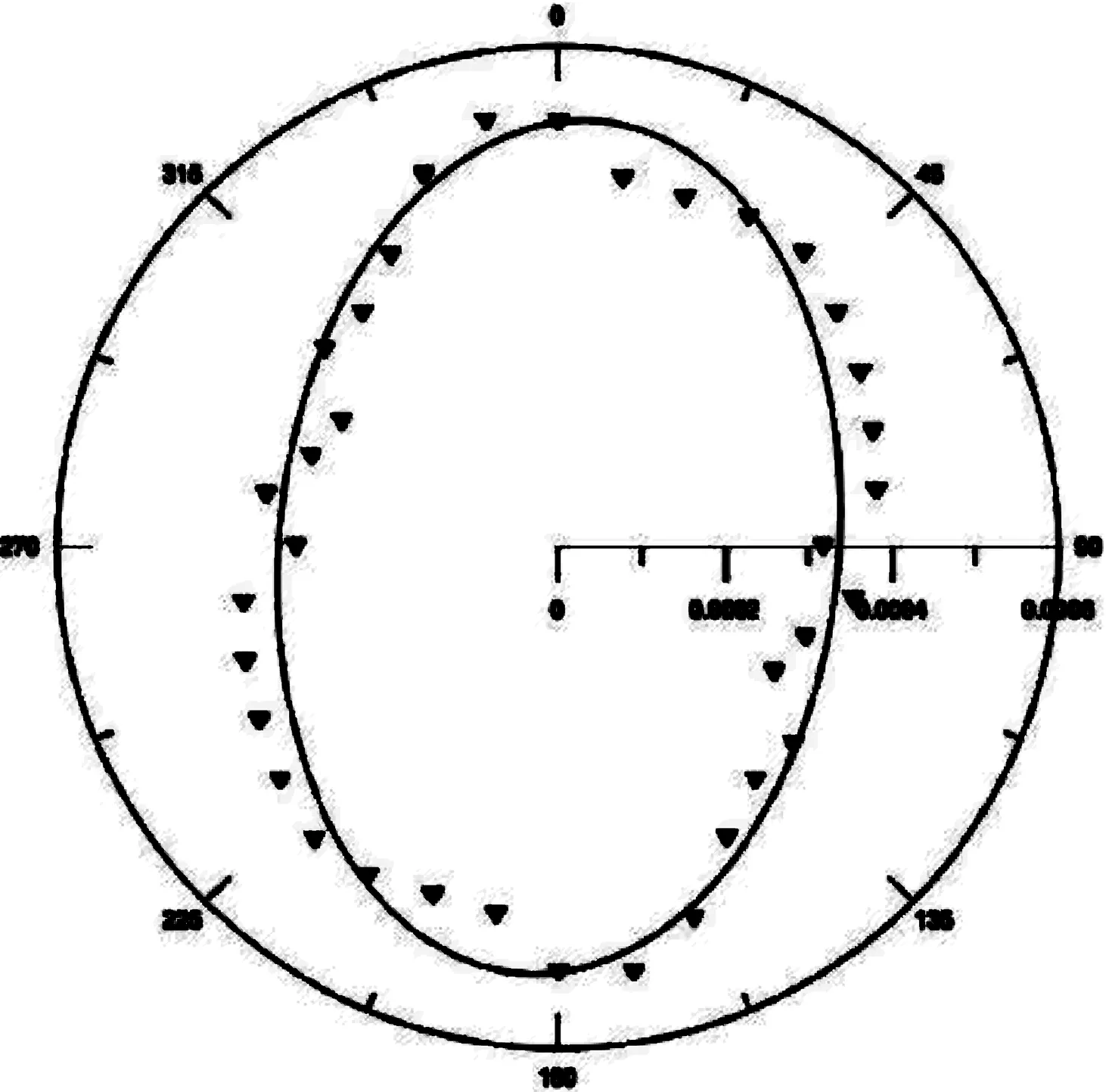
图 4 30 m×15 m区域渗透系数与椭圆曲线拟合Fig.4 Matching of permeable coefficient and elliptic curve in 30 m×15 m area

表3 正交长迹线裂隙岩体REV存在性Tab.3 REV existence of orthogonal long stitch fractured rock

4 结论

综上所述,当正交裂隙迹线长度大于10 m时,对于岩体的等效多孔介质性质可得出以下结论：

1)在裂隙岩体等效连续介质性质研究中,其等效性质与裂隙的间距及迹线长度的组合形式有着密切的联系.一般情况下裂隙的迹线越长、间距越密,其岩体性质越接近连续介质,水力学性质也越接近多孔介质.

2)当裂隙平均间距小于4 m时,REV一定存在,且小于100 m×50 m.而REV的具体尺度需要具体问题具体分析.

3)当裂隙平均间距大于6 m时,岩体可能无法等效多孔介质模型.

文中介绍的方法可以有效地用于裂隙岩体的水力学作用的研究,并且结论比较可靠.但也可以看出,在其研究过程中还需继续考虑裂隙面的开合程度和粗糙度对岩体水力学性质的影响,同时也要进一步讨论多组裂隙的多种方向的组合对渗流的影响.

[1] 周志芳.裂隙介质水动力学原理[M].北京：高等教育出版社,2007：2-3.

[2] Paul A.Witherspoon.Effect of Size on Fluid Movement in Rock Fractures[J].Geophysical Research Letters,1981,8(7)：659.

[3] Bear J.Dynamics of Fluids in Porous Media[M].Dover Publications Inc.,1972.

[4] Long J S,Remer J S,Wilson,et al.Porous Media Equivalents for Networks of Discontinuous Fractures[J].Water Resources Research,1982,18(3)：645-658.

[5] Öhmam J,Niemi A.Upscaling of Fracture Hydraulics By Means of an Oriented Correlated Stochastic Continuum Model[J].Water Resources Research,2003,39(10)：1277.

[6] Öhmam J,Niemi A,Chin F.A Regional-scale Particletracking Method for Nonstationary Fractured Media[J].Water Resources Research,2005,41(3)：1-16.

[7] Baghbanan A,Jing L.Hydraulic Properties of Fractured Rock Masses with Correlated Fracture Length and Aperture[J].International Journal of Rock Mechanics and Mining Sciences,2007,44(5)：704-719.

[8] 吴月秀,刘泉声,刘小燕.岩体节理粗糙度系数与统计参数的相关关系研究[J].岩石力学与工程学报,2011,20(S1)：2593-2598.

[9] 刘晓丽,王恩志,王思敬,等.裂隙岩体表征方法及岩体水力学特性研究[J].岩石力学与工程学报,2008,27(9)：1814-1821.

[10] 张莉丽,王云,张辛,等.低延展性裂隙岩体REV存在性研究[J].现代地质,2013,27(3)：743-749.

[11] 张莉丽,张辛,王云,等.非常低延展性裂隙岩体REV存在性研究[J].水文地质工程地质,2011,55(5)：20-25.

[12] 张辛.基于等效渗透张量的裂隙岩体表征单元体存在性研究[D].北京：中国地质大学(北京),2010.

[13] 于青春,陈德基,薛果夫.岩体非连续裂隙网络水力学特征[J].地球科学：中国地质大学学报,1995,39(4)：474-478.

[14] Wang M,Kulatilake P H S W,Um J,et al.Estimation of REV size and three-dimensional hydraulic conductivity tensor for a fractured rock mass through a single well packer test and discrete fracture fluid flow modeling[J].International Journal of Rock Mechanics and Mining,2002,39(7)：887-904.

Discussion on REV existence and average fracture spacing of orthogonal long stitch fractured rock

ZHANG Xin1,2,SONG Hong-wei1,3,YU Qing-chun4,ZHANG Li-li5
(1.State Key Laboratory for Geomechanics and Deep Underground Engineering,China University of Mining and Technology,Xuzhou,Jiangsu 221116,China;2.School of Economic Management and Humanity,Jiangsu Jianzhu Institute,Xuzhou,Jiangsu 221116,China;3.School of Mechanics and Civil Engineering,China University of Mining and Technology,Xuzhou,Jiangsu 221116,China;4.School of Water Resources and Environment,China University of Geosciences,Beijing 100083,China)

Respective element volume(REV)of fractured rock is objective response of scale effect of hydraulic feature and property of REV decides the rationality and reliability of selecting hydraulic parameters of rocks.Based on verifying the reliability of FractureToKarst by theoretical derivation and multiple linear regression analysis,this paper discusses the relationship between REV existence and average fracture spacing of orthogonal long stitch fractured rock,as well as reasonable size of REV.Meanwhile,it calculates permeable coefficient tensor of REV with statistical method.

fractured rock;orthogonal long stitch;respective element volume;permeable coefficient;average spacing

TU 452

2095-3550(2014)01-0021-05

2013-12-20

江苏建筑职业技术学院科技计划项目 (JYA13-39)

张辛 ,男,江苏徐州人,讲师,博士研究生.

E-mail：malkwax@163.com

(责任编辑：赵国淮)