复合射孔枪爆压数值分析与动态塑性设计准则
2014-10-27霍一飞舒淑宁刘荫忠
霍一飞,舒淑宁,刘荫忠,田 毅
(1.西北工业大学 航空学院,陕西 西安 710072;2.西安通源石油公司,陕西 西安 710065)
1 引言
复合射孔的结构设计离不开工况载荷,也离不开设计准则。否则该设计只是经验之谈,无法成为科学技术加以传承。在复合射孔过程中,爆燃压力除了与炸药本身所具有的化学能相关外,火药的装药量也对爆压的峰值以及脉宽有密切的影响。长期以来工程结构设计一直沿用的强度理论,无论是静强度还是动强度,都无法移植应用到射孔枪结构设计体系之中。这是因为射孔枪的结构设计既需要完成动态设计,又需要进行塑性设计分析。而目前现有设计理论体系中缺乏这类动态塑性设计准则,因此,这种动态塑性流变设计准则将会成为射孔枪结构设计的主要依据,建立该准则的意义就显得十分重要。
爆燃压力载荷实验的研究文献很多,主要探讨载荷与装药关系的道理;这里应用LS-DYNA爆炸冲击软件分析复合射孔的爆燃载荷也是一种数值试验方法,能够大量节约复合射孔器的设计成本。LS-DYNA是美国为武器设计提供的分析软件,它以Lagrange算法为主,兼有Euler算法;以显式求解为主,兼有隐式求解功能;以结构分析为主,兼有热分析、流体-结构耦合功能;以非线性动力分析为主,兼有静力分析功能。LS-DYNA还具有很广泛的分析功能,可模拟许多二、三维结构的物理特性。射孔枪设计的文献也不少,但是除了实验摸索、验证和说明之外,没有任何设计准则可以直接应用在结构设计中。虽然射孔枪的行业标准已经完成,并且规定了射孔后枪身胀形量的标准,但是如何做到这一标准却是一个不断实践和理论升华的过程,也是本文抛砖引玉的目的之一。
通过LS-DYNA软件对不同装药量所产生的压力进行了数值模拟,以得到不同装药量下复合射孔的载荷规律。通过现有的强度设计准则比较和分析,探索一种全新的动态塑性流变的设计方法,期望能够真正用于的射孔枪结构设计之中。
2 理论基础
2.1 火炸药的状态方程
爆轰产物状态方程式炸药爆轰C-J状态之后的爆轰产物系统中各物理量(压力、体积、温度)之间的关系,JWL状态方程能够比较精确的满足描述爆轰产物的膨胀驱动过程。从状态方程中可以看到,炸药爆炸产生的压力除了与炸药本身所含有的化学能有关之外,火炸药所处环境的体积也是影响爆压的原因之一。因此有理由推断,火药除了能够提供与炸药耦合时候的压力外,其在炸药爆炸时候挤占的体积也会增加炸药爆炸产生的压力。
JWL状态方程:
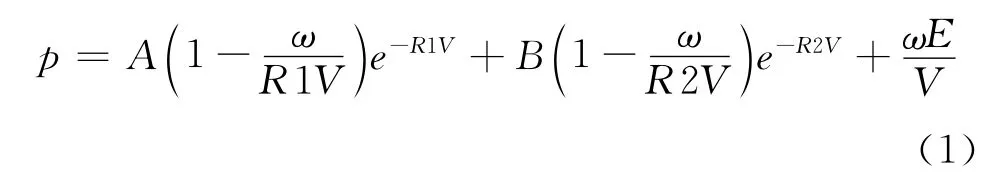
式中A,B,R1,R2,ω —材料常数;E—初始内能;V—相对体积。其中RDX炸药的参数如下表1所示:

表1 RDX炸药材料参数
2.2 材料动态本构模型
Johnson-Cook模型是一个基于经验的材料本构关系式。此模型是大应变、高应变率和高温状态下的金属本构方程。射孔枪32CrMo4材料采用Johnson-Cook热粘性本构方程:
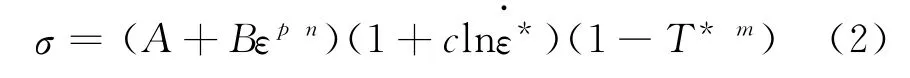
式中εp—等效塑性应变;等效塑性应变率;T*—相对温度。
由试验研究确定的射孔枪材料32CrMo4的五个参数如下表2所示。据此,得到32CrMo4动态塑性流变特性的Johnson-Cook材料本构模型,能够用于LS-DYNA爆燃数值仿真中。

表2 射孔枪身材料动态本构方程的相关参数
3 数值模拟及结果分析
3.1 复合射孔爆压数值分析
用LS-DYNA软件进行建立有限元模型进行数值模拟。其中图1为复合射孔的枪身内部几何结构(a)以及网格剖分(b),采用轴对称模型计算。对几何模型进行单元剖分,单元类型为六面体网格。火药单元、炸药单元、药形罩单元、射孔弹壳体单元、空气单元用任意拉格朗日欧拉网格(ALE)划分,射孔枪身单元用拉格朗日网格划分。其中火药单元、炸药单元、药形罩单元、射孔弹壳体单元与空气单元共节点,空气单元网格覆盖射孔枪单元网格。

图1 射孔枪枪身结构和网格剖分
如图2所示射流密度云图,射孔时枪内形成射流杵体,并且该射流穿透了射孔枪壁。
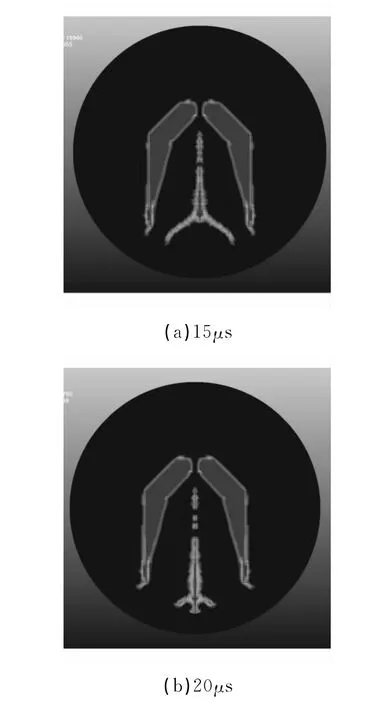
图2 射流过程的射流密度云图
为了研究复合射孔爆燃的空间体积对爆压的影响,分别将火药装药量调整为0g(火药将不占体积)和15g计算,得到的对比曲线如图3所示,该曲线为射流前端区域(非射流区)的压力曲线。图3中横坐标单位是毫秒ms,纵坐标单位为GPa。
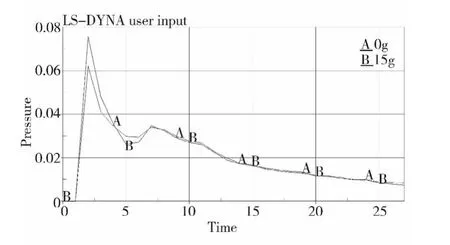
图3 不同装药体积的射流前端区域爆压曲线
由于火药在射孔后3ms开始燃烧,从图3可以看出在1ms到3ms之间出现压力峰值,火药装药量为15g的爆压峰值大于0装火药的爆压峰值,这说明复合射孔爆燃压力峰值的影响因素不仅是炸药以及火药的化学能,还与复合射孔爆燃空间有关。下面分别计算了装药量为15g、25g、35g、40g、50g时枪身内壁与射流轴垂直区的压力,计算结果得到如图4所示的压力曲线。图中的横坐标单位是毫秒ms,纵坐标单位为GPa。
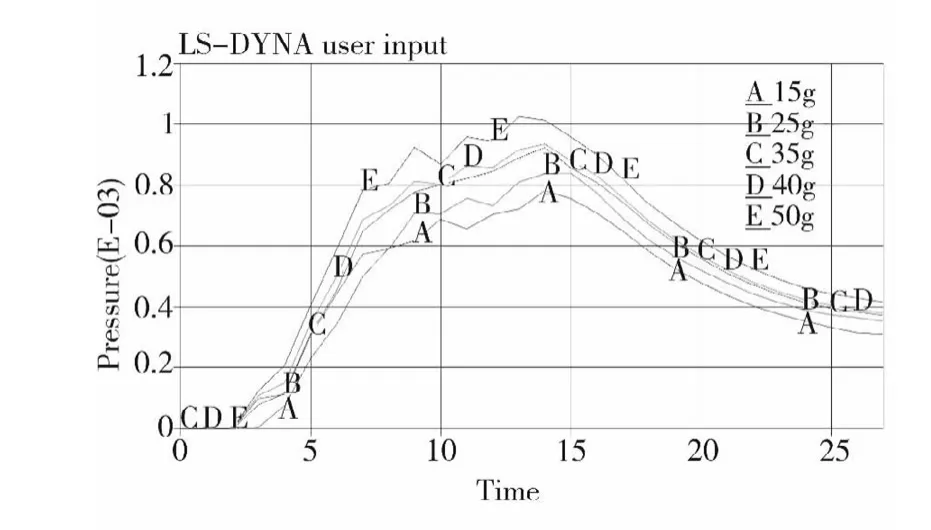
图4 不同装药量压力曲线
通过观察图4的曲线,火药装药量除了对压力峰值有影响(如图5(a)所示的压力峰值与装药量的递增关系曲线)之外,对峰值区的脉宽也有影响,这是由于火药燃烧是产生的高温高压对外膨胀做功,火药越多,做功就越大,反映到P-T曲线上就是压力峰值的脉宽与火药装药量成正比,综合考虑不同装药量下火药的比冲能,将P-T曲线压力对时间积分,如式(3),得到如图5(b)所示的装药量的比冲能曲线。可以看到随着火药装药量与爆炸比冲成正比关系。
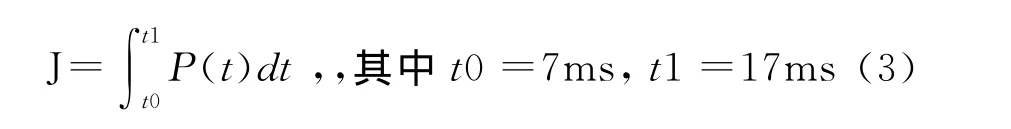
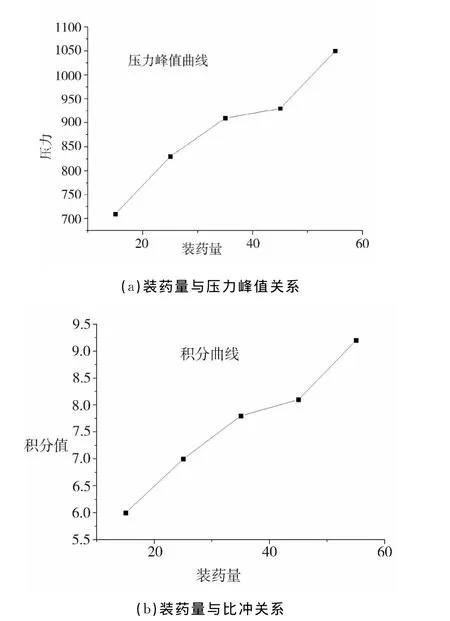
图5 复合射孔装药量与压力和比冲关系
3.2 塑性数值模拟及结果分析
根据射孔枪塑性变形以及复合射孔爆压的数值模拟结果,射孔弹爆炸以及火药燃烧产生的爆压大于弹性极限载荷,小于极限塑性载荷,因此射孔枪必然存在塑性变形。随着枪身内压力的不断增加,射孔枪从弹性变形状态进入到塑性状态,在枪身内壁形成塑性区,并且塑性区在卸载后出现了残余变形。
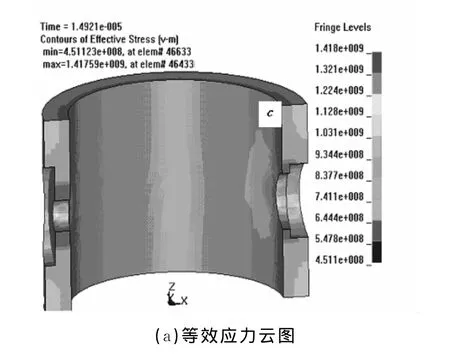
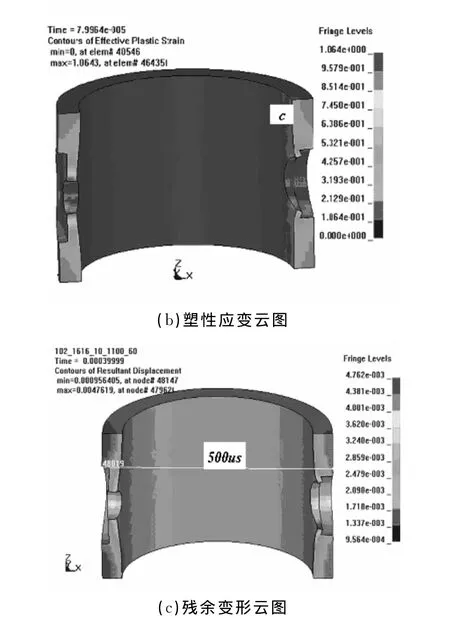
图6 射孔枪身的应力、塑性应变与残余变形
图6(a)为枪身的等效应力云图,射孔枪结构大部分的应力水平进入塑性应力状态。从图6(b)中可以看出最大塑性应变值出现在射流孔和泄压孔的边界。当压力超过弹性极限载荷时,射流孔和泄压孔从弹性状态进入塑性状态,即在内壁出现塑性区。图6(c)是射孔枪的残余变形量,可以看到孔口边界存在的最大变形量为4.8mm。
复合射孔不同装药量的爆压存在差异,这种差异传导到结构上也对应产生应力、应变和变形的差异。图7分别绘制了不同装药量下的枪身应力、应变曲线,表明在不同的装药量下,复合射孔器最大的应力和应变响应关系。
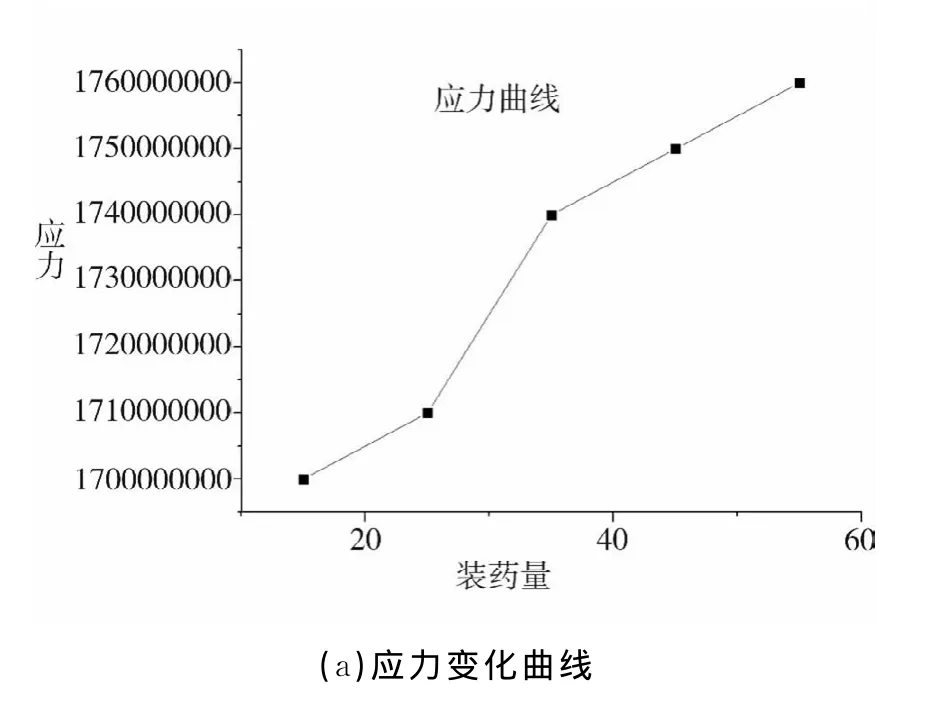
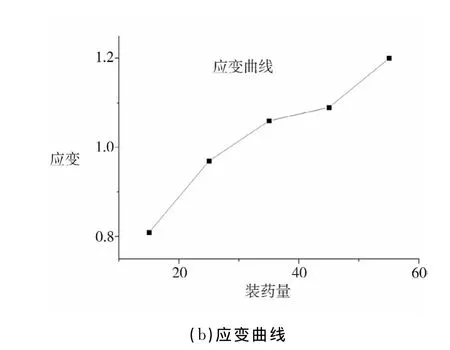
图7 复合射孔枪结构对装药量的影响
4 弹塑性设计准则
4.1 静态强度设计准则
基于Tresca屈服准则,在不考虑枪身外壁压力情况下的枪身结构准静态弹性载荷为:
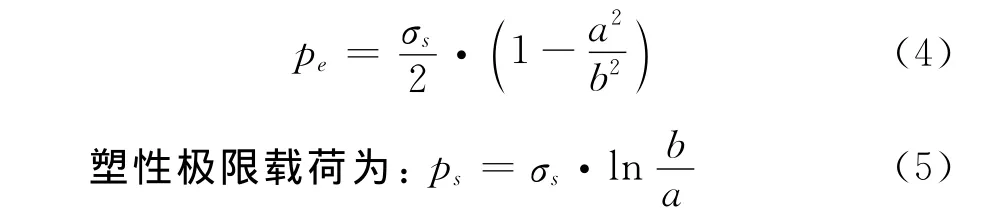
式中a,b为枪身内外径。枪身材料静态屈服强度为835MPa的32CrMo4钢,选用壁厚为10mm的102枪计算,得到在准静态下射孔枪弹性极限载荷为:Pe=158MPa,塑性极限载荷为:Ps=230MPa;枪身材料动态屈服强度为1215MPa的32CrMo4钢,同样得到在动态下射孔枪弹性极限载荷为:Pe=291MPa。Tresca强度理论计算结果比对见表3,从表3可以看出在准静态载荷条件下对枪身强度设计的最大承载载荷远远小于数值模拟得到的载荷,因此用静强度和动强度准则设计塑性变形的射孔枪,缺乏实际应用意义。
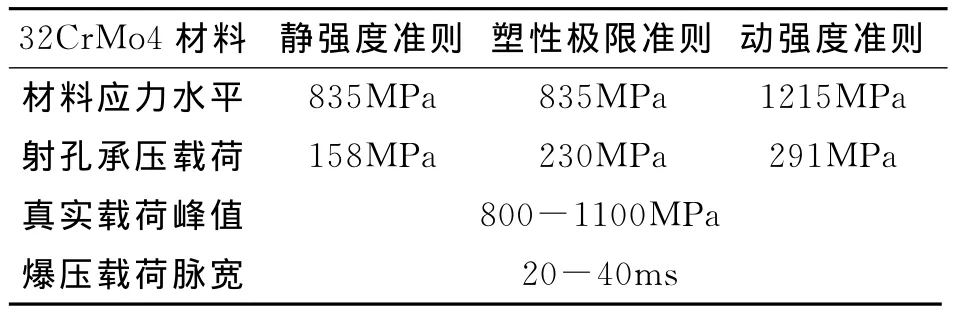
表3 静强度、动强度、塑性流变设计的极限载荷
4.2 动态塑性设计准则
强度校核结果与数值结果的比较,说明静强度弹塑设计准则无法应用到复合射孔器的设计之中:静强度和塑性极限差异大,动强度屈服也不对,因为这里还存在一个时间的因素没有考虑,因此,需要一个与时间相关的动态塑性流变设计准则。基于冲量守恒定律,射孔枪爆燃所产生的载荷P(t)随着时间变化,射孔枪身材料动态塑性应变 也随时间变化。如此,射孔枪身的动态塑性流变设计就应该满足式(6)的不等式,也就是动态塑性流变设计的新方法。动态塑性设计新方法既然已经提出来,就需要大量的理论细节完善和实验验证,最终才能够成为复合射孔器的动态塑性流变设计准则,也是复合射孔器基础研究的一个发展方向。
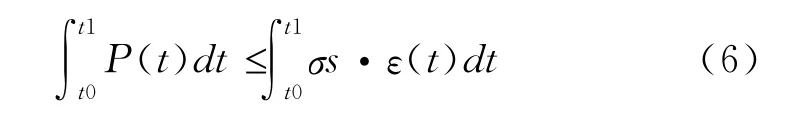
式中,t0、t1为内压峰值区间的时间区间,σs为枪身材料动态屈服极限;ε(t)为塑性应变。
动态塑性设计新方法既然已经提出来,就需要大量的理论细节完善和实验验证,最终才能够成为复合射孔器的动态塑性流变设计准则,也是复合射孔器基础研究的一个发展方向。以一个一维塑性变形设计问题为例,则式(6)可以改写为式(7),具体设计过程仍然离不开结构冲击变形的数值仿真,需要确定其中应变收敛的时差参数Δt。
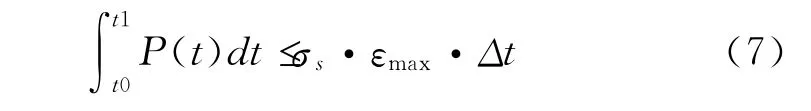
式中的εmax为工程设计许用的最大塑性应变。
5 结语
通过上述的数值研究,得到如下几点结论:
(1)数值模拟的结果,解释了装药量与爆燃载荷之间正相关的关系,爆压的峰值和脉宽都随着装药量的增加而增加;其后,火药持续燃烧的爆燃载荷加大了爆燃载荷峰值的脉宽;
(2)射孔枪在爆燃载荷作用下,应力、塑性应变、变形量主要集中在孔口的纵轴向边界部位,在射流孔口边界处应力、应变的变化更为剧烈,枪身从这一点开始发生塑性变形,并随着压力的增加塑性区不断扩大;
(3)静态载荷与动态载荷对枪身的作用有明显差异,传统设计准则不适用于动载荷的强度设计,需要建立新的结构动态塑性流变设计准则。
(4)提出新的设计方法源于冲量守恒理论,细节仍然需要进一步发展,以方便动态塑性设计的应用。
[1]赵莉,赵开良,申梅英,等.不同类型复合射孔器火药燃烧特征研究[J].测井技术,2006,30(1):44-46.
[2]刘会娟,刘荫忠,田毅,等.复合射孔爆炸与燃烧机理数值模拟分析[J].测井技术,2012,36(1):78-83.
[3]赵铮,陶钢,杜长星.爆轰产物JWL状态方程应用研究[J].高压物理学报,2009,24(3):277-282.
[4]朱公志,张建为,朱敏捷.石油射孔枪墙体结构优化设计[J].科学技术与工程,2011,11(25):6049-6053.
[5]陶亮.射孔枪几个结构设计问题的数值分析[J].测井技术,2006,30(1):25-28.
[6]张昭,刘亚丽,胡海飞,等.射孔枪射孔过程数值模拟及参数控制[J].塑性工程学报,2008,15(6):151-156.
[7]王培禹,刘荫忠,徐波.准静态下射孔枪的枪身弹塑性理论分析[J].西部探矿工程,2011,7:70-72.
