基于华氏宏观经济数学模型的高等职业教育动态投入产出模型

张 静，权双燕

（1.东莞职业技术学院 继续教育学院，广东 东莞 523808；2.陕西理工学院 数学与计算机科学学院，陕西 汉中 723000）

伴随着经济的发展和产业结构的变化，对高技能人才的培养已经成为必然趋势。高等职业教育作为培养高技能人才的重要途径，已经得到许多学者的关注，其中高职教育投入产出关系受到普遍重视。早在60年代，美国学者就开始关注学校的投入与产出的关系。我国学者也根据投入产出的一般原理，应用华西里·列昂惕夫宏观经济模型提出了我国教育系统的投入产出模型。其后，黄银忠、阮陆宁等人在文献［1］的基础上进行了深入研究。20世纪80年代初，华罗庚建立了华氏宏观经济数学模型，该模型是在劳动生产力未充分发挥的情况下，得到的投入、产出关系。本文分析了高等职业教育的产业特性和产业流程，建立了高等职业教育投入产出表，并结合华氏宏观经济数学模型建立了高等职业教育的动态投入产出模型。应用该模型可对学生培养量、教师需求量、固定资产租金使用量等教育因素进行预测。

1 模型分析

教育系统和生产系统一样，其活动结果有一定的产出，从此意义上讲，教育系统具有一定的产业特征。教育系统的产出是合格的学生，其中一部分留在教育系统进行再培养、学习，称为教育系统的中间产品，另一部分学生达到毕业要求，进入社会，称为教育系统的最终产品。高等职业教育作为教育系统的一部分，同样具有完整的产业特征。其主要投入包括学生、教职工、固定资产、教育费用；产出包括学生、科研成果、社会服务。因为高等职业教育主要的产出是学生，所以本文只考虑学生作为产出的情况。并假设培养出的学生的质量相同。并根据教育系统的特点，将周期定为学年。

高等职业教育系统可以看为包含3个培养部门的模型。培养流程分析如图1所示。

第1部门为1年级学生培养部门：培养出1年级学生Q1人，投入教师L1人，平均工资为ω万元／人·年；投入U1万元的其他费用，此费用用于学校正常运转开支；投入rK1亿元固定资本租金，其中r表示固定资本租金率，K1表示固定资本。

第2部门为2年级学生培养部门：培养出2年级学生Q2人，投入教师L2人，平均工资为ω万元／人·年；投入U2万元的其他费用，此费用用于学校正常运转开支；投入rK2亿元固定资本租金，其中r表示固定资本租金率，K2表示固定资本。

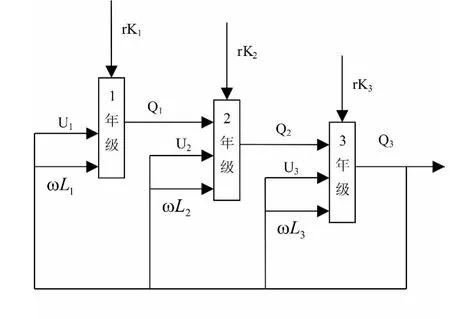
图1 学生培养流程

第3部门为3年级学生培养部门：培养出3年级学生Q3人，每人p万元（它反映的是每个毕业生售予社会的价格，可以用培养一个高职毕业生国家给予的全部费用或民办学校收取的全部学费来衡量），所以可以把第3部门看做“生产”资金的部门，即“生产”毕业生售出获得资金。投入教师L3人，平均工资为ω万元／人·年；投入U3万元的其他费用，此费用用于学校正常运转开支；投入rK3亿元固定资本租金，其中r表示固定资本租金率，K3表示固定资本。

在考虑不增加投资的基础上，每个部门需要的费用和教师工资可以看做均来自第3部门“生产”的资金。因为固定资本的投入是预先投入的，所以固定资本租金的投入可看做外部投入。

2 投入产出表

根据以上模型分析，投入产出表见表1。

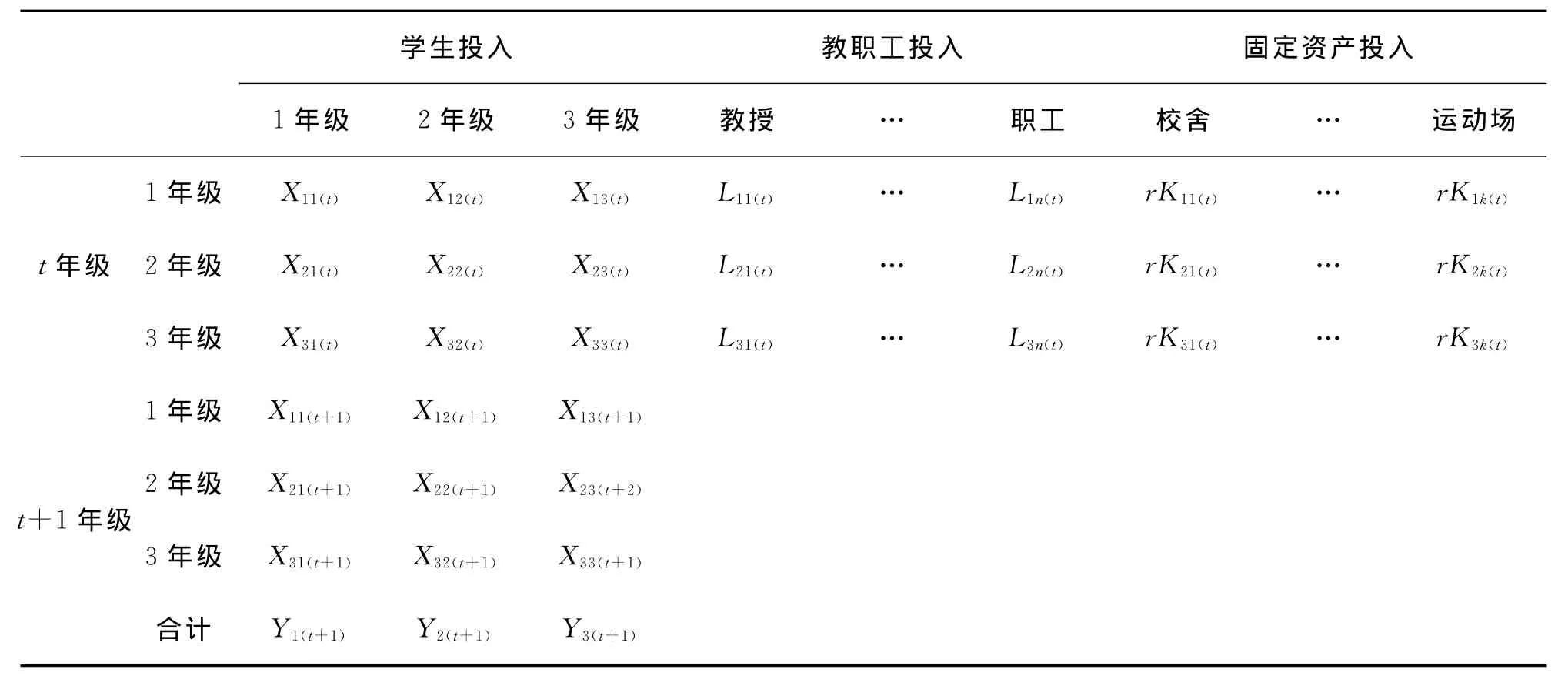
表1 投入产出表

Xi3：表示培养i年级学生投入教育费用，此费用来自售出3年级毕业生获得的资金，包括教师工资以及学校正常运转的其他费用。

Xij（j≠3）：表示培养i年级学生投入的j年级学生数。

Lij（t）：表示t学年培养i年级学生投入的第j种教职工数。

rKij（t）：表示t学年培养i年级学生投入的第j种固定资产的租金。

Yi（t＋1）：表示t学年各部门的产出，也可表示t＋1学年各部门的投入。

投入产出表写成矩阵形式为：

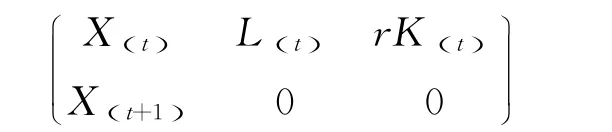
其中X（t），X（t＋1） 分别表示t学年和t＋1学年学生投入产出矩阵，L（t）表示t学年教职工投入矩阵，rK（t）表示t学年固定资产租金投入矩阵。

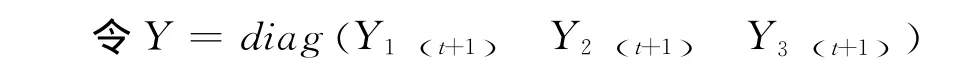
3 模型的建立

根据以上建立的模型和高等职业教育的投入产出表，在不考虑增加教育投入的基础上，教育系统是一个封闭的系统，并假设教育规模不受现有条件的限制，因此上述建立的教育模型的特征与华氏宏观经济模型类似，可以用华氏宏观经济数学模型描述高等职业教育的投入产出关系。

设第一年（t＝0）各个年级的投入为 Y0＝（Y1（0）Y2（0）Y3（0））。t年后，各个年级的产出为 Yt＝（Y1（t）Y2（t）Y3（t））。如果学生消耗系数矩阵A不因年份而改变，那么 Y（0），Y（t）满足以下关系：

定理 如果A是一个不可约的非负方阵，则对任何非A的正特征向量X（0），必有一l0＞0，使正整数l≥l0时，X（l）＝A－lX（0）一定是变号向量，即此向量有些分量是正，有些是负。

定理说明对于高等职业教育系统，各个年级学生的培养量也要以A的正特征向量为比例。否则，若干年后，某个年级的学生培养量为负值。

4 模型的应用

4.1 预测学生培养量

t学年各年级学生的培养量可由 Y（t）＝Y（0）A－t式求得。

4.2 预测各类教师的需求量

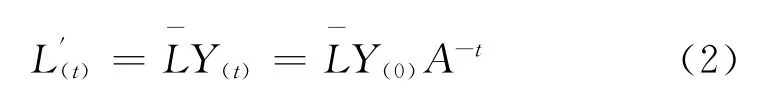
4.3 预测固定资产租金使用量

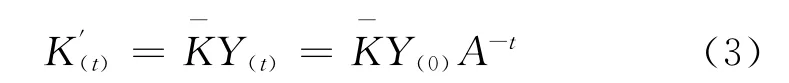
5 结语

高校在固定资产的管理过程中，其价值是不进行折旧处理的。因此，在确定固定资本租金率r时，只有借鉴企业同类固定资产折旧标准，同时兼顾高校使用的实际，对企业折旧标准进行适当的修正。在教育过程中，常会受到师资、校舍等因素的制约，从而限制教育事业的发展，而本模型没有将各种限制因素加以考虑，所以模型还存在一定的局限性，可以进一步对模型进行优化研究。虽然模型存在局限性，但对研究高等职业教育的投入产出关系仍具有一定实际意义。

［1］钟契夫，陈锡康.投入产出分析［M］.北京：中国财政经济出版社，1987：627－634.

［2］黄银忠.教育系统投入产出模型及其应用［J］.系统工程理论与实践，1991（3）：51－58.

［3］阮陆宁，曹小秋，秦澎涛.地方普通公立高等教育投入产出模型分析［J］.南昌大学学报（理工版）.2002，26（3）：235－238.

［4］华罗庚.计划经济大范围最优化的数学理论（I）［J］.科学通报，1984，29（12）：6－11.

［5］徐大举，刘家壮，窦方军.有消费或投资的华氏宏观经济模型［J］.经济数学，2003，20（2）：27－32.

［6］向蓉美.投入产出法［M］.四川：西南财经大学出版社，2007.