双层金属环形阵列的太赫兹表面等离子体研究
2014-10-25杨冬晓
夏 松,杨冬晓
(浙江大学信息与电子工程学系,浙江杭州310027)
1 引言
自1998年Ebbesen观测到周期性孔阵列金属薄膜的光波段透射谱出现由表面等离子体(surface plasmon,SP)引起的超强透射效应以来[1],这种周期性阵列在太赫兹(terahertz,THz)频段的透射研究也取得了很大的进展[2]。表面等离子体是由电子沿着金属/介质界面连续振荡而形成的电磁波,可分为传播型表面等离子体(propagating surface plasmon,PSP)和局域型表面等离子体(localized surface plasmon,LSP)[3]。
传播型表面等离子体是由电子的连续振荡激发并可在界面上传播的电磁波。周期性的阵列可以为激发传播型表面等离子体提供动量补偿。单层或多层金属的周期性阵列结构的太赫兹透射研究表明,传播型表面等离子体、波导以及表面等离子体之间的耦合都能对共振透射效应产生影响[4-5]。局域型表面等离子体则是微小金属颗粒上的电子振荡,局限在金属颗粒周围的非传播性的电磁波[6]。其共振频率与金属颗粒的尺寸、形状以及周围的介质环境有关[7]。目前,传播型表面等离子体和局域型表面等离子体的技术已经在激光等领域应用[8]。
本文采用由MIT开发的基于时域有限差分(finite-different time-domain,FDTD)法的 MEEP软件包[9]对金属-介质-金属结构的太赫兹透射特性进行仿真。分析表明,太赫兹的共振透射受传播型表面等离子体、局域型表面等离子体、准波导效应以及表面等离子体之间耦合的影响。
2 仿真分析
金属-介质-金属三层结构由两层金属和中间层石英介质组成,两个金属层上刻有相同的环形空气槽,如图1插图所示。相关参数为:介质厚度d,金属厚度h,周期P,内径rin和槽宽w,因此可得到外径rex和中心半径 rcen为:rcen=rin+w/2,rex=rin+w。

图1 结构的频谱透射率谱(插图为一个单元结构的示意图)Fig.1 Calculated THz transmittance of structure(Inset:schematically illustration of a cell)
光滑的金属表面不能束缚电磁波,但是周期性的阵列结构则可以实现电磁波的束缚,此时金属可近似为完美导体(perfectelectricconductor,PEC)[10]。
石英在太赫兹波段的折射率为1.9,参数选择为:h=10 μm,d=100 μm,P=200 μm,rin=80 μm,w=10 μm,仿真中太赫兹波沿z方向垂直入射。计算得到该结构在0.2~0.6太赫兹的频谱透射图,如图1所示。可以看到有两个很明显的透射峰,它们由表面等离子体引起,分别标记为f1和f2,两个频率中间有一个明显的凹陷,并在以f1和f2为边界的频段内,其透射率相对较高,两个峰的边缘比较陡峭。
图2表示f1和f2处沿y方向电场Ey在各个平面的分布图。在x-y平面,场主要集中在空气环内,金属表面几乎不存在场,如图2(A1)、2(A2)所示;在x-z平面,Ey几乎存在自由空间,金属表面几乎没有场,如图2(B1)、2(B2)所示;在y-z平面,场集中在空气环里,如图2(C1)、2(C2)所示。因此,Ey场几乎分布在自由空间和介质中,几乎不存在于金属表面,这与表面等离子体特性是相吻合的。
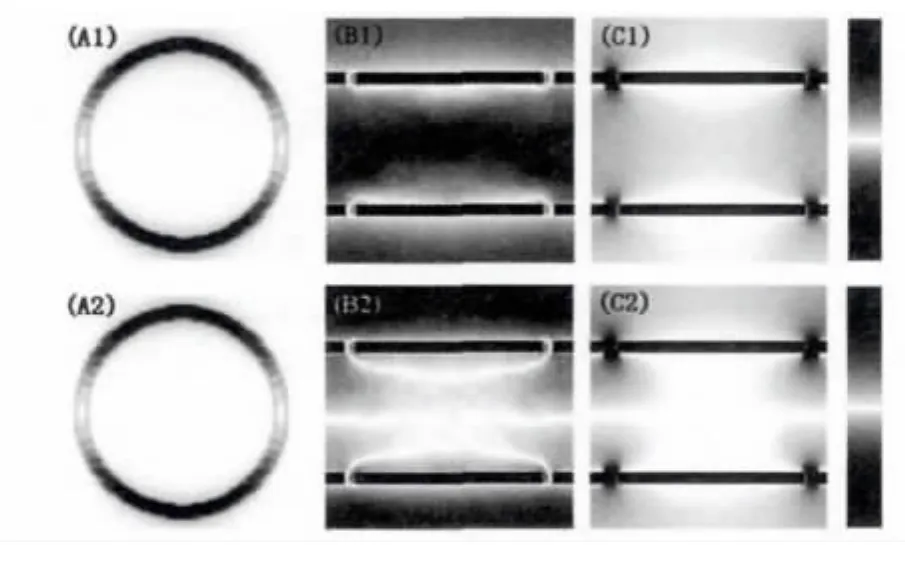
图2 (A1)~(C1)和(A2)~(C2)分别表示了f1和f2处Ey的分布(其中(A1)与(A2)、(B1)与(B2)和(C1)与(C2)分别表示的是在x-y、x-z和y-z平面的Ey分布图)Fig.2 Distributions of Ey are shown for f1 in(A1)~(C1)and f2in(A2)~(C2)
f1和f2处沿z方向电场Ez在各个平面的分布如图3所示。在x-y平面,f1和f2的场分布几乎一样并集中于金属边缘,如图3(A1)、3(A2)所示;在x-z平面与y-z平面,Ez分布都反映了场束缚在金属的表面和边缘,只是f1和f2在同一面上Ez的方向不同,如图3(B1)、3(B2)、3(C1)、3(C2)所示。Ez主要集中在金属的边缘的特性,也是表面等离子体一个重要的特征。

图3 (A1)~(C1)和(A2)~(C2)分别表示了f1和f2处Ez的分布(其中(A1)与(A2)、(B1)与(B2)和(C1)与(C2)分别表示的是在x-y、x-z和y-z平面的Ez分布图)Fig.3 Distributions of Ez are shown for f1in(A1)~(C1)and f2in(A2)~(C2)
基于以上场分布的分析,电磁波在结构中的传输过程如下:入射波在第一层金属的上表面激发出表面等离子体,这时由Ey表征的入射波转化为由Ez表征的表面等离子体,一直传播到空气环的边缘,再通过环的耦合作用,将表面等离子体恢复为由Ey表征的电磁波,在环中传播到第一层金属的另一表面,并激发出相应的由Ez表征的表面等离子体,沿着此表面传播,然后表面等离子体再次转化为由Ey表征的电磁波,在中间层介质传播到第二层金属。接下来的过程与以上类似,电磁波最后离开金属-介质-金属结构。
为进一步探究这些共振现象,计算得到了该结构沿x方向的色散曲线,如图4所示。

图4 沿x方向的色散曲线图(当a=200 μm时,纵坐标频率标尺为1.5 THz)Fig.4 Calculated dispersion relation along x direction(For the case of a=200 μm,the coordinate frequency is c/a=1.5 THz)
这里,重点研究光锥线以下的模式,因为光锥线以上的模式是自由空间的散射模式,其能量不能束缚在金属表面,只有光锥线以下的模式才能束缚在金属表面[3]。可以看到,全部在光锥线以下的模式有4条,分别标记为 P1-mode、P2-mode、P3 -mode、P4-mode。对于比较浅的金属孔,金属两表面的传播型表面等离子体通过金属孔中的衰减场进行耦合,形成新的传播型表面等离子体模式[11]。当金属的厚度与入射波的波长和结构的其他尺寸相比足够小,会发生传播型表面等离子体的耦合并产生上述模式。另外,还有一条模式与光锥线交叉,记为T-mode。对于环中间的金属片,电荷振荡仅仅局限在其周围,可以看做孤立“粒子”,这样会激发局域型表面等离子体。典型的局域型表面等离子体具有横模与纵模两条色散模式[12]。根据这两条模式的特征得知,此处的T-mode是由局域型表面等离子体主导的横模。
结合图1与图4,共振峰f1和f2分别对应于P3-mode和T-mode,分别由传播型表面等离子体和局域型表面等离子体激励。同时,透射率中的通带(f2-f1)位置也对应色散曲线的阴影部分,其中P3-mode和T-mode在kx=0.5处(M)耦合减弱,相应的能量由于非线性作用,转移到其他频率,形成如图1所示的凹陷。随着频率的偏移,交叉点M的耦合作用逐渐减小,使得相应的透射率逐渐增大,如图1所示。
此外,图4的模式仅仅对应于存在于金属表面的模式,只有能够穿过整个结构的模式才能在透射率中显示出来,其他存在于金属表面的模式在z方向上衰减掉了,因此在图1透射率谱中没有相应的共振峰。
通过对透射谱、场分布、色散等特性的仿真分析,此结构可用于实现太赫兹滤波、谐振、调制等功能。
3 结构参数对特性的影响
改变结构参数,计算得到了共振峰位置的变化特性。图5显示了f1和f2随内径rin和外径rex的变化。图5(a)中参数为:P=200 μm,d=100 μm,h=10 μm,rex=90 μm。图 5(a)中,rin有一临界值rc=30 μm。当rin< rc时,f2稳定在0.79 太赫兹,而rin>rc时,f2随rin增大而减小。这是由于太小的金属片尺寸rin(<0.1λ),会使局域型表面等离子体效应逐渐消失。此外,当rin从10 μm增加到80 μm时,f1从0.49太赫兹减小到0.35太赫兹。图5(b)中参数为:P=200 μm,d=100 μm,h=10 μm,rin=40 μm,当 rex从45 μm增加到90 μm时,f2几乎稳定在0.73太赫兹,而f1从0.67太赫兹减小到0.45太赫兹。可见,f2对金属片半径rin很敏感,体现了局域型表面等离子体的特性。
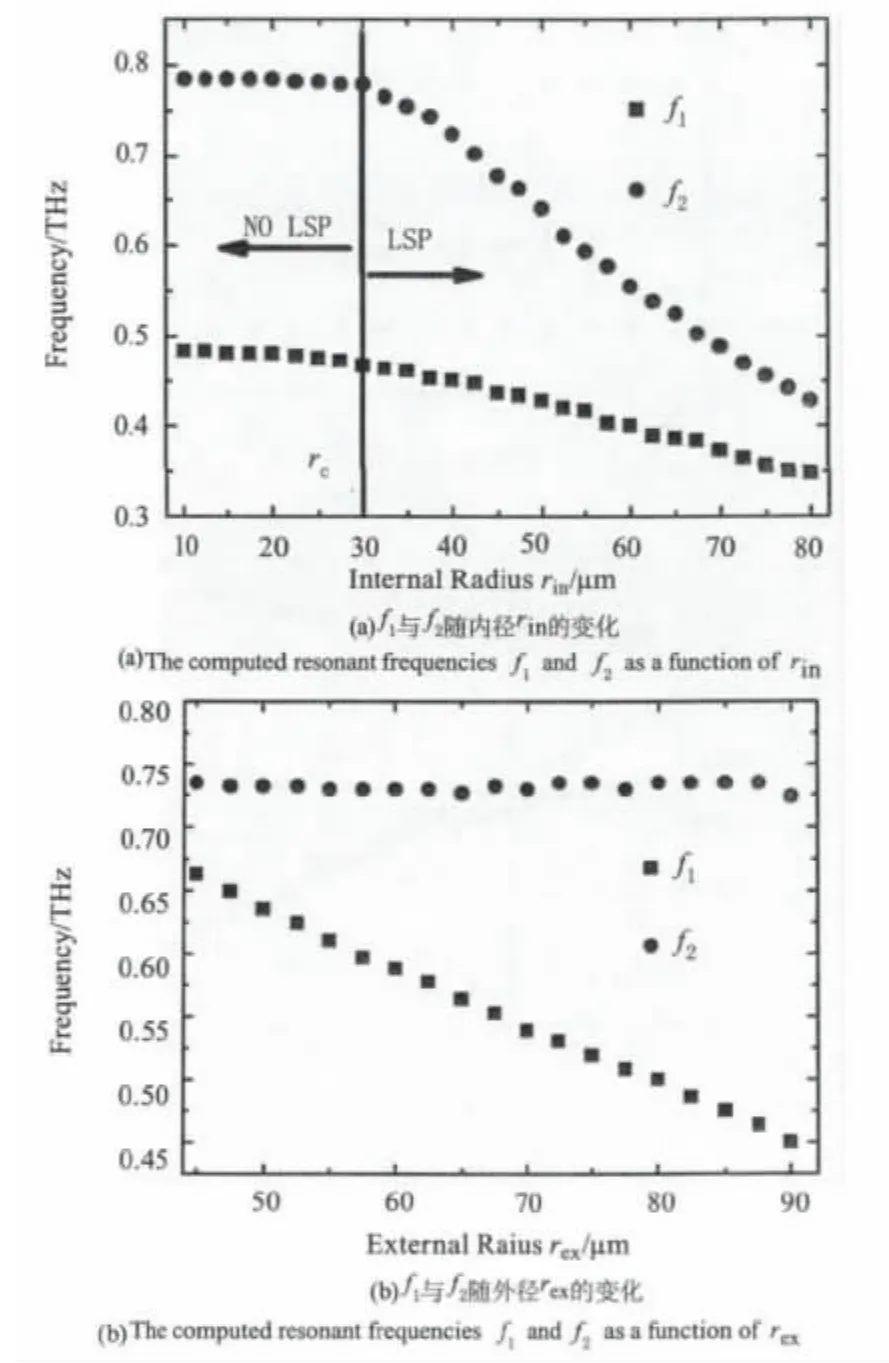
图5 f1与f2随内径、外径的变化
图6为f1和f2随中心半径rcen和宽度w的变化趋势。当 rcen=70 μm,w 从5 μm 增加到40 μm 时,f1几乎保持不变,f2则逐渐增加,如图6(a)所示。其他参数为:P=200 μm,d=100 μm,h=10 μm,rcen=70 μm。插图分别为双层圆孔阵列一个单元示意图及其太赫兹透射率谱。当rcen=70 μm并且w从10 μm增加到80 μm时,f1从0.64太赫兹减小到0.46太赫兹,f2则比较缓慢地增加。为了解释这种现象,引入一种类似结构:双层圆孔阵列结构,其单元结构与透射率分别如图6(a)与6(b)的插图所示。
图6(b)插图中出现了两个峰与一个谷,记为fL,fH和fW。其他参数为:P=200 μm,d=100 μm,h=10 μm,rcen=45 μm。插图分别为双层圆孔阵列一个单元示意图及其太赫兹透射率谱。实际上,Wood Anomaly和传播型表面等离子体的基模决定了fH和fW,而fL由波导效应和表面等离子体之间的耦合形成[11]。类似的,当改变孔径rex时,其共振峰fL与fH频移特性如图6所示。为方便比较,用w通过w=rex-rin来表示rex。根据图6(a)与6(b),当w(rex)增加时,fH几乎保持不变,fL则逐渐减小。
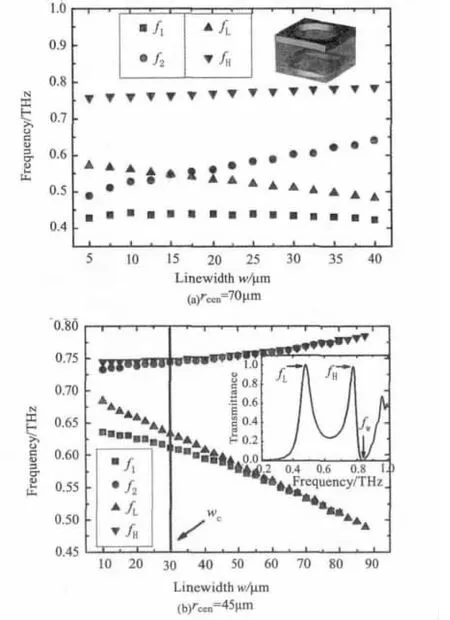
图6 环的宽度f1,f2,fL和fH的影响
当rcen=45 μm,如图6(b)所示,环的宽度w有一临界值 wc=30 μm。当 w > wc,f1、f2分别和 fL、fH几乎重合,这表明当粒子尺度(rin=rcen-w/2)足够小,粒子作用逐渐消失,环形阵列就近似为圆孔阵列,导致局域型表面等离子体的消失和相应传播型表面等离子体模式的产生;当w<wc,局域型表面等离子体的作用逐渐出现,表现出来的是环形阵列与圆孔阵列的共振峰不重合。
当rcen=70 μm,如图6(a)所示,此时环形阵列中局域型表面等离子体作用能够体现出来,f1几乎保持不变,f2逐渐增加。用准波导效应可以解释谐振频率f1:空气环可近似为准矩形波导,其长边的平均值为2πrcen,短边为w,截止频率由矩形的长边决定[4]。因此,尽管w的变化引起了该准矩形波导短边的变化,但是其截止频率依然不受影响。该近似需要满足两个条件:一是rcen足够大,保证局域型表面等离子体能够起作用;二是w足够小,保证环可以近似为矩形。此外,由于w的变化影响了rin的值,当w增大时,f2会逐渐增加。
改变rcen的值,本质上改变的是环的内径rin和外径rex,仿真结果与以上分析是一致的,如图7(a)所示,其他参数:P=200 μm,d=100 μm,h=10 μm,w=10 μm。图7(b)给出了 f1和 f2随周期P的变化情况,其他参数:rin=80 μm,d=100 μm,h=10 μm,w=10 μm。
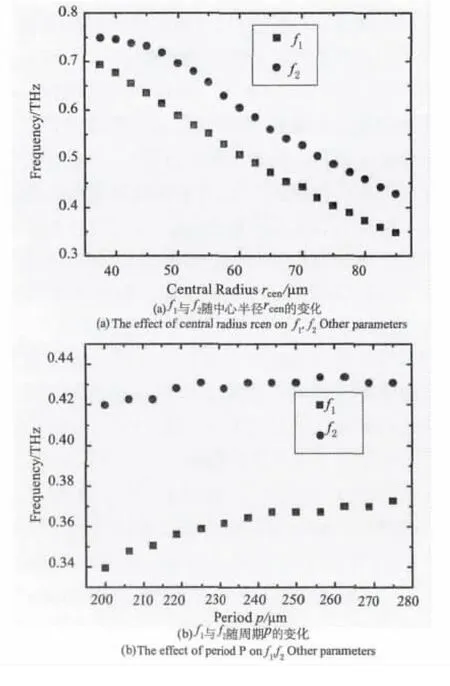
图7 f1与f2随中心斗径和周期变化图
对于大量粒子,粒子间有近场耦合与远场耦合两种方式[13]。近场耦合需要粒子间距足够小,一般为纳米数量级[14];远场耦合要求粒子尺寸比粒子间距小的多[6]。这里,两相邻金属片边缘相距为40 μm ≤ Δd=P -2 rin≤ 115 μm,远大于纳米数量级;另一方面,金属片直径为2 rin=160 μm,比粒子间距大。因此,近场和远场耦合条件均不满足,耦合不会发生,则 f2不会随着周期而变,如图7(b)所示。
当周期P增加时,传播型表面等离子体共振峰f1增加,如图7(b)所示,这与公式 f传播型表面等离子体=c(i2+j2)1/2/(Pneff)的变化趋势相反。由于该公式近似计算传播型表面等离子体的共振频率,对于相对复杂的结构就不适用了,此时有其他耦合模式产生了相应的作用。
介质层的特性(厚度d与介电常数εd)对太赫兹传输的影响如图8所示。图8(a)中εd=1,图8(b)中 εd=3.61,其他参数:P=200 μm,rin=80 μm,h=10 μm,w=10 μm。根据以上关于表面等离子体的传输与能量流动机制的分析,上层金属要激发下层金属的表面等离子体必须会经过中间层介质,因此无论是传播型表面等离子体还是局域型表面等离子体都必然会受到影响。
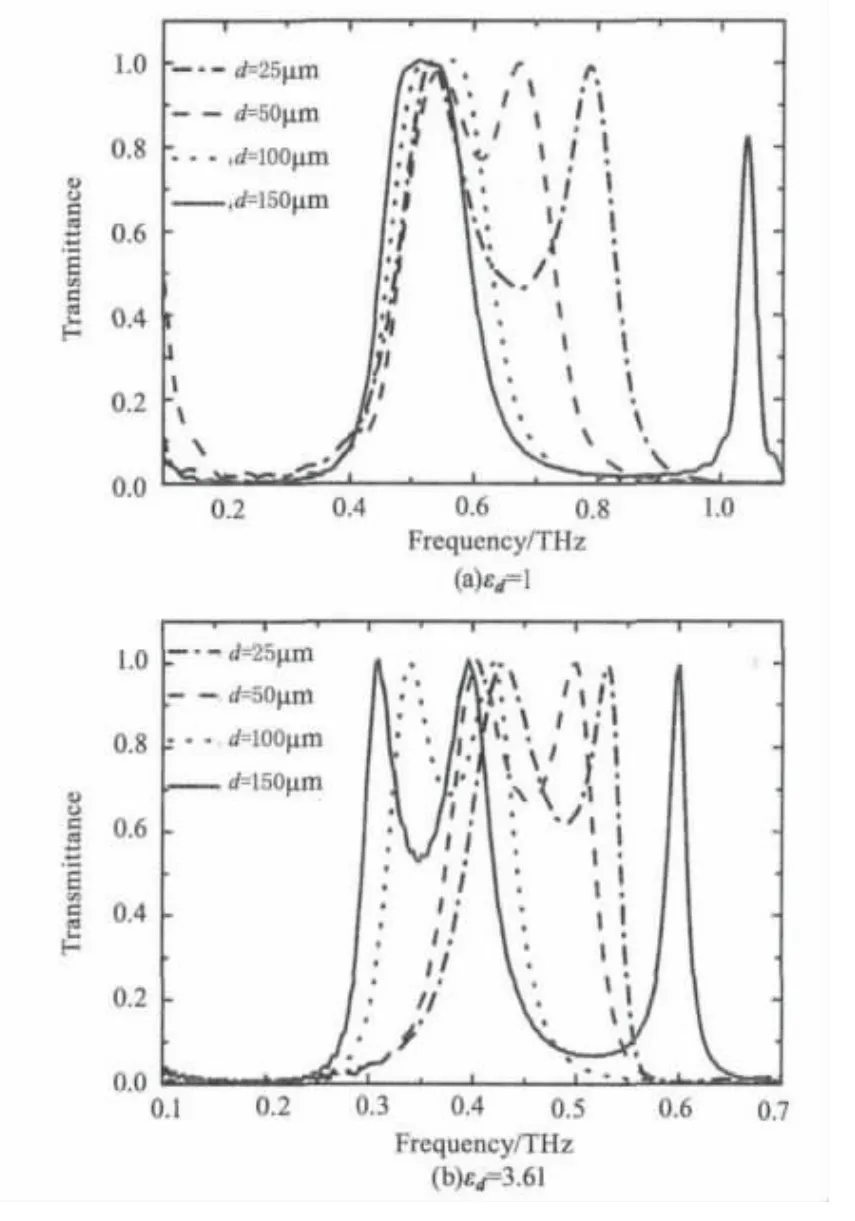
图8 f1与f2随介质厚度d的变化Fig.8 The calculated THz transmittance for various d
图8中,当 εd=1且d由25 μm 增加到150 μm时,f1几乎保持不变;而当εd=3.61时,随d的增加f1逐渐减小。对于传播型表面等离子体模式,这种三层结构可用等效介电常数模型来近似[5]:当金属层有亚波长结构而介质层没有时,中间层介质介电常数及其厚度共同决定传播型表面等离子体的特性,即当金属两界面的介质介电常数相等时传播型表面等离子体几乎不受介质厚度影响,而当金属两界面的介质介电常数不相等时,传播型表面等离子体受介质厚度的影响较大,因而得到上述结果。
对于上下金属层间局域型表面等离子体的耦合,因为介质厚度对应的是z方向的尺度,该方向的粒子尺寸应该是金属的厚度h,它比粒子(金属片)的间距(介质厚度d)小得多,满足远场耦合条件,所以会发生局域型表面等离子体远场耦合。图8显示εd和d都对局域型表面等离子体的共振产生影响,共振峰f2随介质厚度d增加而降低,其变化趋势与参考文献[6]一致。
结合上述关于表面等离子体的传输过程,本质上来说,电磁波沿z方向的传播必然会受到中间介质影响,比如散射、吸收等,也必然会发生各种耦合。
电子云的行为可以用来帮助更好地理解这些现象。对于局域型表面等离子体,由于孤立离散的电荷振荡集中于金属片表面,局域型表面等离子体的激发、耦合以及从金属片的一个表面到另一个表面的传输,需要的是表面电子的转移,电子的这些行为受金属片的特性影响较大,比如尺寸、形状等。但是对于传播型表面等离子体的激发、耦合和传输等,孔、狭缝、环等耦合结构显得尤为重要,它们不仅是一个传输通道,而且能够改变传播型表面等离子体的相关特性。本文中,整个表面的表面电流将会分配到每一个环,连续的表面电流截断成许多局域化的电流集中在环的周围,环的特性会影响传播型表面等离子体的传输。所以,f1受中心半径和周期支配,f2受金属片半径主导,以及表面等离子体之间的耦合等特性符合这两个共振峰的形成机制。
可见,以上分析除了进一步揭示表面等离子体在太赫兹透射中的作用外,也为设计具有不同性能的太赫兹功能器件奠定了基础。
4 结论
本文采用时域有限差分法研究了双层金属环形阵列结构的太赫兹透射特性,产生的共振峰主要是由表面等离子体引起。共振频率处的电场分布和沿x方向的色散曲线进一步表明了表面等离子体的作用,其中f1和f2分别由传播型表面等离子体和局域型表面等离子体主导。对该结构的参数变化对特性影响的研究表明,周期对f1影响大,而金属片的半径对f2影响大,体现了传播型表面等离子体和局域型表面等离子体的特征。在一定条件下,空气圆环可以近似为准波导,对f1有很大影响。此外,中间层介质的几何与光学特性也会影响各个界面上的表面等离子体耦合,进而对太赫兹的透射产生相应影响。该结构的太赫兹共振透射特性有望在太赫兹波功能器件方面得到实际应用。
[1] T W Ebbesen,H J Lezec,H F Ghaemi,et al.Extraordinary optical transmission through sub-wavelength hole arrays[J].Nature,1998,391(6668):667 -669.
[2] M Dragoman,D Dragoman.Plasmonics:Applications to nanoscale terahertz and optical devices[J].Progress in Quantum Electronics,2008,32(1):1 -41.
[3] S Hayashi,T Okamoto.Plasmonics:visit the past to know the future[J].Journal of Physics D:Applied Physics,2012,45(433001):1 -24.
[4] Z C Ruan,M Qiu.Enhanced transmission through periodic arrays of subwavelength holes:the role of localized waveguide resonances[J].Physical Review Letters,2006,96:233901.
[5] R Ortuño,C García - Meca,F J Rodríguez - Fortuño,et al.Role of surface plasmon polaritons on optical transmission through double layer metallic hole arrays[J].Physical Review B,2009,79:075425.
[6] S A Maier.Plasmonics:Fundamentals and applications[M].London:Springer,2007.
[7] P Frank,J Srajer,A Schwaighofer,et al.Double - layered nanoparticle stacks for spectro-electrochemical applications[J].Optics Letters,2012,37(17):3603 - 3605.
[8] P Berini,I Leon.Surface plasmon - polariton amplifiers and lasers[J].Nature Photonics,2012,6:16 -24.
[9] A F Oskooi,DRoundy,M Ibanescu,P Bermel,J D Joannopoulos,S G Johnson.MEEP:A flexible free - software package for electromagnetic sumulations by the FDTD method[J].Computer Physics Communications,2010,181(3):687-702.
[10] A Pors,E Moreno,L Martin - Moreno,J B Pendry,et al.Localized spoof plasmons arise while texturing closed surfaces[J].Physical Review Letters,2012,108:223905.
[11] L Rao,D X Yang,L Zhang,et al.Design and experimental verification of terahertz wideband filter based on double- layered metal hole arrays[J].Applied Optics,2012,51(7):912-916.
[12] S Y Park,DStroud.Surface - plasmon dispersion relations in chains of metallic nanoparticles:An exact quasistatic calculation[J].Physical Review B,2004,69:125418.
[13] B Lamprecht,G Schider,R T Lechner,et al.Metal nanoparticle gratings:influence of dipolar particle interaction on the plasmon resonance[J].Physical Review Letters,2000,84(20):4721 -4724.
[14] M Quinten,A Leitner,J R Krenn,et al.Electromagnetic energy transport via linear chains of silver nanoparticles[J].Opt.Lett.1998,23(17):1331 -1333.
