基于FAHP的住房公积金社会效益评价指标体系研究
2014-10-24骆智娟周云
骆智娟,周云
(苏州科技学院 土木工程学院,江苏 苏州215011)
基于FAHP的住房公积金社会效益评价指标体系研究
骆智娟,周云
(苏州科技学院 土木工程学院,江苏 苏州215011)
为了全面科学衡量住房公积金的社会效益,根据影响住房公积金社会效益的关键指标,进行了住房公积金社会效益评价指标体系的研究.在建立住房公积金社会效益评价指标体系的基础上,采用模糊层次分析法(FAHP),构建了具有多层次、多指标的复合体系.研究结果表明:支持保障性住房面积、保障房受益家庭数、本期个贷发放金额、购房提取额和租房提取额等单项指标为影响住房公积金社会效益的关键指标.建议政策制定部门从上述几个指标调整相关条款,提高住房公积金的社会效益.
住房公积金;社会效益;评价指标体系;模糊层次分析法 (FAHP);关键指标;
近年来住房公积金的社会效益受到关注.相关研究从住房公积金对住房消费、社会福利及公积金运行效率等角度对住房公积金的社会效益进行了评价[1-3],但缺乏完整的常态化的评价指标体系,评价角度和方法较为单一,提出的改进措施和政策建议顾此失彼,不能保证评估结果全面真实,科学有效.因此,构建全面的、科学的、客观的评价指标体系,对政策制定、调整与建议,显得格外必要而迫切.
确定住房公积金社会效益评价指标权重时,最难把握的是指标彼此间重要性量化的确定.本文运用模糊层次分析法(FAHP),构造模糊判断矩阵,确定指标相对于总目标的相对权重,提高评价指标体系的信度和效度,从而较准确地衡量住房公积金社会效益的整体水平.为住房公积金制度建设提供帮助,为政府主管部门制定住房公积金相关政策法规提供参考.
1 住房公积金社会效益评价指标体系的构建原则
1)全面性原则.全面性原则是要求评价指标体系应从不同层面反映出住房公积金社会效益的总体情况.因此,设计的评价指标应该涵盖住房公积金所产生社会效益的主要方面.
2)一致性原则.一致性是指住房公积金社会效益的评价指标体系与住房公积金社会效益评价的目标之间的一致性.住房公积金社会效益评价的目标是帮助政府制定政策,促进住房市场均衡发展.因此,在设计和选择社会效益评价指标时,应从住房公积金社会效益评价的总目标出发来设定和选择评价指标.
3)层次性原则.层次性原则是要求评价指标不但能反映对住房公积金整体社会效益水平,而且应相互协调,便于全面评价所研究的对象.即评价指标体系中的单项评价指标之间,在内涵、计算方法、计算时间和范围等方面,要求相互衔接,力求全面、系统地反应住房公积金社会效益各构成要素之间的内在联系及其规律性.
2 基于模糊层次分析法的数学模型
1)递阶层次模型指标体系构建.在模糊层次分析法中[4],指标体系结构包括目标层、准则层和指标层.其中最高层为目标层,中间层为准则层,是连接着目标层和指标层.中间层的因素属于目标层,同时又受指标层的影响.最底层为指标层,也称为因素层.
2)模糊判断矩阵的构建.在建立了模糊层次分析结构模型之后,可以根据层次结构模型和专家判断信息,构建各层次因素的模糊判断矩阵.本文在进行因素的比较判断时,采用三角模糊数方法来定量[5].三角模糊数定义为

式中:L ij≤M ij≤U ij,且L ij,M ij,U ij∈[1/9,1]∪[1,9]分别表示aij的下界、中值和上界.在FAHP的应用中,可将多为评估专家用1- 9标度法表示的判断抽象为三角模糊数,其中Lij=min(Bijk),M ij,U ij=max(Bijk).Bijk表示第K个专家对Ci、Cj两因素相对重要性的判断.
有多位评估专家对各层次各因素的相对重要性进行判断,并用三角模糊数表示出来,即形成模糊判断矩阵为A=[aij]=.其中,三角模糊数aij表示C i对C j的相对重要性.
3)去模糊化.去模糊化的方法有多种,本文采用下式方法将三角模糊数aij去模糊化[6].

式中:=(M ij-L ij)a+L ij,U aij=U ij-(U ij-M ij)a,分别为aij的a截集的左端值和右端值.a为决策者偏好系数,值a的大小反映了判断的不确定性,a=0时不确定性最大;λ表示决策者的风险容忍度,λ值越小表示决策者越乐观,反之,越悲观.这里,分别取a=0.5,λ=0.5表示理性的决策者.
去模糊化后,矩阵如下式所示.

4)计算单层次权重子集.对于去模糊化的判断矩阵(Aa)λ,计算满足[(Aa)λ-λ]W=0的特征根和特征向量,并将特征向量归一化.对应于最大特征根λmax的特征向量,就是相应元素单排序的相对权重向量.本文应用AHP层次单排序的方根法,计算去模糊化后各判断矩阵的权重向量.
5)一致性检验.上述得到的权重值是否合理,还应该进行一致性检验.当结果偏离一致性时,则表明该矩阵不具备满意一致性,该权重向量不能作为决策依据.一致性指标CI和随机一致性比率CR分别由下式给出:

式中:n为判断矩阵阶数,IR为平均一致性指标.当CR<0.1或者CI等于0时,即认为判断矩阵具有满意一致性,说明权重分配是合理的,否则要重新调整判断矩阵,直至具有满意一致性为止.
6)排序.排序是计算下一层元素对于上一层准则相对重要性的权重,由最高层到最低层逐层计算,从而得到各指标对目标层的重要性权重,按下式计算.

式中:Wj为第j个指标相对于目标层的权重;Wi表示准则层Ci相对于目标层的权重;Wij表示指标C ij相对于准则层C i的权重.
3 住房公积金社会效益评价指标体系分析
1)构建递阶层次模型.根据上述分析评价指标体系的构建原则,结合模糊层次分析法的特点,采用调查问卷的形式,征询了相关专家对评价指标体系的意见,然后进行统计处理,形成了三层四类共20个指标组成的住房公积金社会效益评价指标层次结构模型,如图1所示.

图1 住房公积金社会效益评价指标体系Fig.1 Evaluation index system of socia benefit of housing fund
2)构造模糊判断矩阵.成立由5位专家组成的评价小组.每位专家根据对各层因素两两之间相对于上层因素的重要性,按1- 9标度法进行比较.综合5位专家的判断结果,取5位专家中最大值、最小值和5位专家赋值的几何平均数,并用式(1)中三角模糊数表示出来,构成模糊判断矩阵.表1为准则层相对于目标层的模糊判断矩阵.
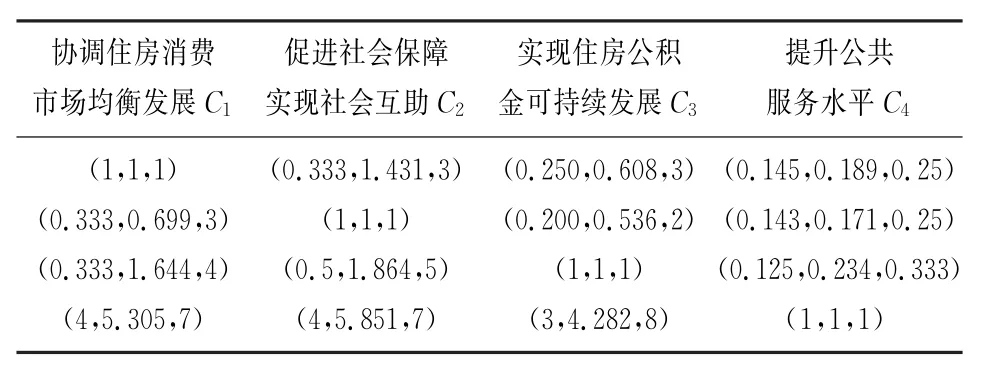
表1 准则层各因素相对于目标层的模糊判断矩阵Tab.1 Fuzzy judgment matrix of criterion layer factors relative to destination layer
3)去模糊化.根据以上方法在构造模糊判断矩阵后,首先去模糊化,再分别计算一级、二级指标权重.在这里只给出运用FAHP法计算一级指标权重的具体算法,二级指标权重计算大致相同,本文只给出计算结果.
根据式(2)和式(3),取a=0.5,λ=0.5对上述模糊判断矩阵去模糊化.从而得到去模糊化后的判断矩阵,见表2.

表2 准则层各因素相对于目标层去模糊化后的判断矩阵Tab.2 Defuzzification judgment matrix of criterion layer factors relative to destin ationlayer
4)层次单排序及一致性检验.应用AHP层次单排序的方根法,可以计算出去模糊化后各判断矩阵的权重向量,计算重要性排序.以一级权重指标的计算为例:



5)一致性检验.
n
=4,
RI
=0.90,
CI
=
=0.019 7,
CR
=
CI
/
IR
=0.022<0.10.它表明判断矩阵具有满意一致性.
因此,得到一级评价指标的权重为G=(0.373,0.365,0.205,0.057).
以此类推,检测每个判断矩阵的一致性,得出各个矩阵都具有满意一致性λmax,一致性检验指标CR及各指标权重见表3.

表3 住房公积金社会效益评价指标权重Tab.3 Evaluation index weights of social benefit of housing fund
4 结论
本文运用模糊层次分析法确定各指标的权重,构建了具有多层次和多指标,相对重要性不同的复合体系,解决住房公积金社会效益评价中的一个难题.并最终得到影响住房公积金社会效益的关键指标.即支持保障性住房面积、保障房受益家庭数、本期个贷发放金额、购房提取额和租房提取额等单项指标.从一定程度上反映出协调住房消费市场均衡发展,促进社会保障.实现社会互助是住房公积金社会效益产生的主要来源.
[1] 杨刚,王红卫.住房公积金制度对上海住房市场量价波动的影响研究[J].上海财经大学学报,2012,14(1):85- 91.
[2] 徐峰,胡昊,丛诚.住房消费中住房公积金的贡献度:以典型城市为例的实证研究[J].建筑经济,2007(4):47- 50.
[3] 李燕,周勇,刘传哲.住房公积金的住房保障作用探析[J].特区经济,2010(8):142- 144.
[4] 韩彦峰,王蕊.基于模糊层次分析的房地产企业并购风险指标体系研究[J].财会通讯,2013(2):110- 112.
[5] Fei J.Yao R M,Yu L H.Fuzzy Analytic Hierarchy Process Application to E—government Performance Evaluation.In Proceedings of the Fifth International Conference on Fuzzy Systems and Knowledge Discovery.V01.3.2008.21- 24.
[6] Liou S,Wang M J.Ranking fuzzy numbers with integral value.Fuzzy Sets and Systems,1992.50(3).40-42.
On evaluation index system of social benefit of housing fund based on FAHP
LUO Zhi-juan,ZHOU Yun
(School of Civil Engineering,Suzhou University of Science and Technology,Suzhou,Jiangsu 215011,China)
In order to evaluate the social benefit of housing fund fully and scientifically,this paper studies on evaluation index system of social benefit of housing fund according to key indexes which influence the social benefit of housing fund.Based on establishing evaluation index system of social benefit of housing fund,this paper establishes a compound system with multiple levels and indexes through fuzzy analytical hierarchy process(FAHP).Results show that indexes including security housing area,number of beneficiary families,granting amount of current loans,and withdrawal amount of house-purchase and house-renting are key indexes to influence the social benefit of housing fund.We suggest that policy makers adjust related policies from aforementioned indexes and improve the social benefit of housing fund.
housing fund;social benefit;evaluation index system;fuzzy analytical hierarchy process(FAHP);keyindexes
C 913.7
A
2095- 3550(2014)03- 0017- 04
2014-06-19
江苏省普通高校研究生科研创新计划项目 (CXLX13_862)
骆智娟,女,江苏徐州人,硕士研究生.
E- mail:cxksh1989@126.com
(责任编辑:陶红林)
