求解优先函数的改进型Floyd方法
2014-10-24吴大非
吴大非
(湖南科技学院 信息技术与教育系,湖南 永州 425199)
有关算符优先文法及其语言的研究虽可往后追溯到Floyd于1963年所开展的工作[1],但其影响深远,仍然是我们分析部分上下文无关语言所采用的重要技术之一。
针对优先语言的分析问题而被设计和引入的自动分析手段叫算符优先分析法。该法包括分析总控程序和操作支持部件即栈两部分。前者是固定的,不因所面对的文法的改变而改变,后者则依据分析对象间的优先关系制约、组织着整个分析过程。因而,优先关系一定意义上可视为算符优先分析法的灵魂所在。因为算符优先分析法简洁易于实现,现已成为借助栈实施表达式处理的经典方法。
优先关系的实施技术主要有矩阵表示法和优先函数两种[1],前者在信息刻画方面清晰详尽,但美中不足是空间损耗大,远不如优先函数带来的优越性能。本文深入探讨优先函数的Floyd计算方法,指出其存在的问题,并给出相应的改进办法。
1 预备知识与背景
算符优先文法(Operator Precedence Grammar, OPG)及其语言自Floyd提出以来,得到了广泛关注和应用。文献[12-14]等是早期的研究,主要致力和介绍语言分析方法的改进与应用。例如在优先关系的实施问题上,Martin在文献[12]基础上解答了有关优先函数计算中涉及的发现和存在性问题。文献[14]又将文献[13]涉及的布尔矩阵予以分块,再利用数学手段在分块阵的分步求值基础上将原有运算重叠于必要的公共空间上,从而获得物理资源利用上的性能提升。
表达式是科学研究过程中经常碰到的数学概念,涉及表达、解读两个环节,一般用以刻画研究对象间的复合、相互表征等问题。算符优先文法除却适合表达式的描述以外,也适合程序语言、半结构数据的描述。如Floyd就以优先文法刻画、分析过ALGOL60。因为它简洁易用,现也是借助栈实施表达式处理的常用方法。
文献[2, 15-16]给出了一些新近成就。著名的VPL ( Visibly Pushdown Language)[17]是既适合描述程序分析问题又能像正规语言那样而易于处理的确定型上下文无关语言。因为算符优先文法可以定义 VPL, 看似无关的两个语言又变得水乳交融起来。这为人们重新考量和关注OPG的价值、应用迎来新的契机。
本工作旨在探讨OPG关键支撑技术即优先函数计算方法的改进问题。为方便后续讨论,先对它的基本知识与问题做一交代。
1.1 基本概念
定义1(算符文法) 一个上下文无关文法叫做算符文法,如果其任何句型中都不含两个及以上相继出现的非终结符。

定义3(算符优先文法) 一个算符文法叫做算符优先文法,如果其任意终结符对之间最多只能满足上述三种优先关系之一。
优先关系一般用矩阵表示。以图1所示的两个算符优先文法为例,它所规定的俩优先矩阵见表1.该表界定了理解句子的一个基本原则,而凭此就可以设计实现一个基于栈的表达式或句子处理算法。这一方法也叫算符优先分析法,是栈的经典应用之一。

图1 算符优先文法
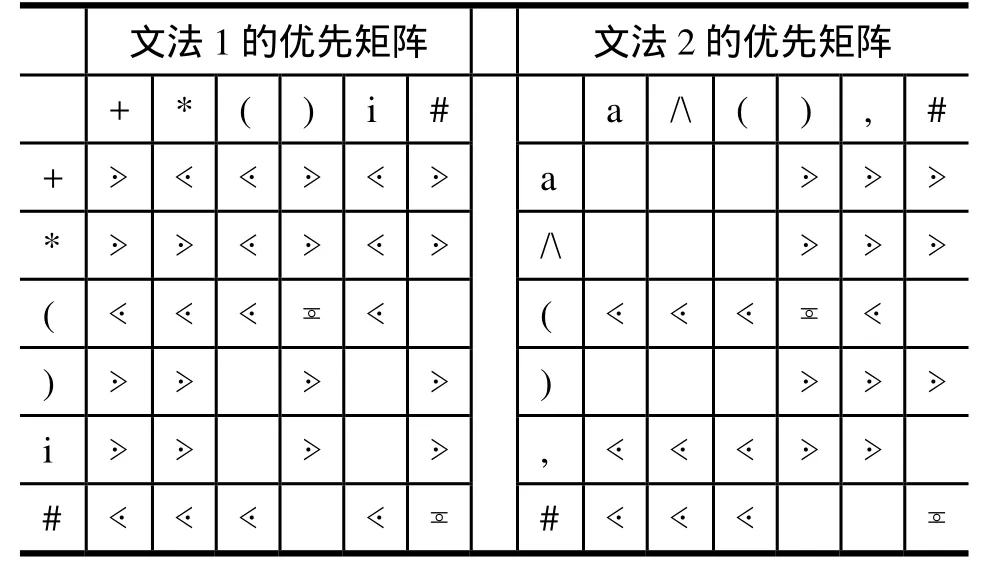
表1 算符优先文法1和2的优先矩阵
定义4(优先函数) 给定算符优先文法及算符优先矩阵,如果存在满足以下性质的函数f、g,则说它们为相应关系的优先函数。
(1)a⋗b,则f(a)>g(b);
(2)a⋖b,则f(a)<g(b);
(3)a≖b,则f(a)=g(b)。
显然优先函数较准确地刻画了优先关系,就存贮而言,可以节省大量空间。
1.2 问题与动机
算符优先语言的分析方法通常叫做算符优先分析法。它的句型分析原理是:以移进-归约的自下而上分析方式,反复读取和处理待分析的表达式或源码,并将分析过程所得的结果保存在分析栈中;归约原则是按最左素短语进行归约,即依据优先矩阵,一旦发现栈顶呈现出可称谓最左素短语的可归约子串,就将该子串替换为适当产生式的左部符号。这一分析过程周而复始,直到所有源码处理完毕。有关更详尽的内容,读者可以参见文献[1, 4-10]。
上述分析原理表明,优先关系控制着移进/归约的实施过程,是算符优先分析法的核心技术与灵魂所在。照实保存优先矩阵不失为一种实现技术,但会消耗过多的存贮资源,总计可达O(n2)存贮单元。因此通常采用优先函数作为其信息压缩手段。这样可将空间消耗量降至O(n)个。
给定算符优先矩阵情形下,优先函数既可通过人为设置也可采用Bell方法或Floyd方法来自动获得。鉴于Floyd方法简洁易于实现,一直沿用至今,以下对它深入分析,以期对其进行有效改进、提升性能。
2 优先函数的计算
2.1 Floyd方法
Floyd方法是便捷易用的优先函数计算方法。它与Bell方法类似,两者均以优先关系矩阵为基础。以下是它的具体描述。由循环体可见,该算法的主要问题是数据的访问或修正量过大,每次迭代都需进行全体优先矩阵元素的检测。这便值得关注,自然成为我们改进的目标。
算法1 (Floyd方法) 设G为算符优先文法, T、P分别为终结符集和相应的优先矩阵, 则优先函数f、g存在情况下可按下述步骤获得[1,5,7-10]:

2.2 改进算法与原理
算法1中fa、gb分别代表f(a)和g(b)的取值。可见,只要fa、gb因循环体的执行有一小小改变就有可能引发f、g的既有计算结果的动荡;而每一动荡的修正、调整又会招致新一轮迭代检测(需n2次检测运算)。特别地,优先矩阵某些情形下还可能是稀疏矩阵。例如假设某算符文法的终结符集为T,关于开始符S的产生式为S→N1a1N2a2…Nm-1am-1Nm,又设各Ni(1≤i≤m)能导出的终结符集相对独立且一道构成T-{a1,…,am-1}的一个划分,则优先矩阵即为稀疏矩阵刻画的优先关系R(⊂T×T )。鉴于此,对算法1进行了必要改进。
下面介绍改进算法的思想和所依据的数学原理。总体而言,我们希望做到:检测、函数调整要有针对性,即尽量调整那些可能需要调整的fa和gb。
在给定优先矩阵的前提下,我们将优先关系按⋖、≖、⋗分成Less、Equal和Great三组(每组中的终结符偶对间都满足同一类优先关系)。进而再设每一组中的优先关系具有一定的局部秩序(依据优先矩阵按行或列序原则组织同类优先关系的排列),如对a ∈T而言,让{a⋖b| b∈T, 且a和b之间满足⋖关系}中的元素占据Less序列(满足“⋖”关系的全体终结符偶对组成的序列)某连续位置区域,那么,针对优先矩阵获得的以下Great、Less序列为改进算法提供了有用的性质。
Less的性质:若Less是按行序原则排列优先矩阵的一切“⋖”关系所得的序列,那么关于g函数的一个增大的变化可能会在Great中引起局部变化,但对于Less中满足f(X)<g(Y )的一切实例具有保向性。
Great的性质:若Great是按列序原则排列优先矩阵的一切“⋗”关系所获得的序列,那么关于f函数的一个增大的变化可能会引起Less的局部变化,但对于Great中满足f(X )>g(Y )的一切实例具有保向性。
根据以上性质,可以改进Floyd算法如下。其中FofModifiedLess表示为了满足Less关系描述而被调整过的f的定义点;GofModifiedGreat表示为了满足Great关系描述而被调整过的g的定义点。
算法2(改进方法):设Less为按行存放的优先矩阵中具有“⋖”关系的偶对序列,Great为按列存放的优先矩阵中具有“⋗”关系的偶对序列,Equal是优先矩阵中一切具有“≖”关系的偶对序列,且初始FofModifiedLess= {a | a⋖b ∈ Less},GofModifiedGreat= {b | a⋗b ∈ Great},则优先函数f、g存在情况下可按下述改进方法获得。


3 例证与分析
为比较和了解两个算法的迭代过程,我们以表1所示的两个优先矩阵为例来检证以上算法。Floyd方法与改进算法的执行对比分别见表2和表3。
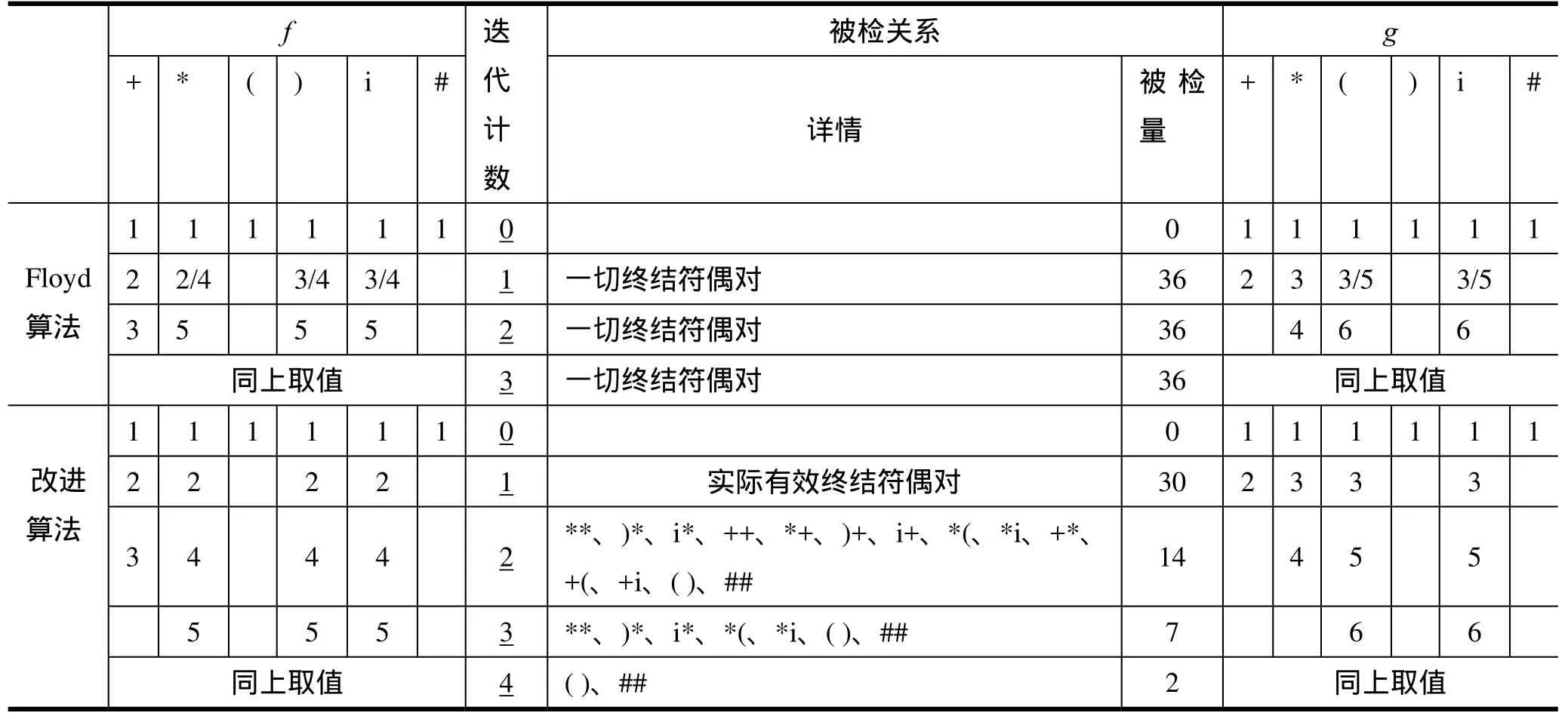
表2 针对优先矩阵1的迭代过程

表3 针对优先矩阵2的迭代过程

Floyd算法1 1 1 1 1 1 0 0 1 1 1 1 1 1 2 2 2/3 2/3 1一切终结符偶对 36 2 2 2 2 3 3 2一切终结符偶对 36 4 4 4同上取值 3一切终结符偶对 36 同上取值改进算法1 1 1 1 1 1 0 0 1 1 1 1 1 1 2 2 2 2 1实际有效终结符偶对 23 2/3 2/3 2/3 2 3 3 3 3 2a,、/,、),、,,、, a、, /、, (、()、## 9 4 4 4同上取值 3 ()、## 2 同上取值
由表2和3可见,两个算法的迭代结果完全一样,但改进算法每次迭代中基本只对需要调整的函数定义进行必要的修正或访问,因而提高了处理性能。就文法1和2的分析(不计初始化)而言,原方法的迭代执行对终结符偶对一共进行了3*36=108次的检测操作或访问,改进方法则对终结符偶对分别进行约53次和34次检测或访问。
4 结束语
优先关系的技术实施问题是算符优先分析法的关键所在。以上分析和改进了一直被广泛采用的Floyd的优先函数计算方法,取得了满意的结果。在改进算法基础上,关系检测操作基本做到量需进行,因而成倍减少了冗余的比较等操作。
[1]R.W.Floyd.Syntactic Analysis and Operator Precedence[J].J.Assoc.Comput.Mach,1963,10(3):316-333.
[2]Alessandro Barenghi,Stefano Crespi Reghizzi,Dino Mandrioli,Matteo Pradella.Parallel parsing of operator precedence grammars[J].Information Processing Letters, 2013,1-11.
[3]D.Grune and C.J.Jacobs.Parsing Techniques: A Practical Guide[M].Springer,2008.
[4]Michael Main,Walter Savitch, Data Structures and Other Objects Using C++ (4thEdition) [M].Pearson Education Asia Limited and Tsinghua University Press,2012.
[5]He Yan-xiang,Wu Chun-xiang,Wang han-fei.Compiler Principle[M].Beijing: China Machine Press, 2010.
[6]Chen Huo-wang, Liu Chun-lin, Tan Qing-ping, et al.Programming Language:Compiler Principle (3rdEdition) [M].Beijing:National Defence Industry Press,2009.
[7]Chen Ying,Chen Shuo-ying,Ji Wei-xing.Compiler Principle[M].Beijing: Tsinghua University Press,2009.
[8]Liu Ming, Xu Lan-fang, Luo Ting.Compiler Principle (3rdEdition)[M].Beijing: Publishing House of Electronic Industry, 2011.
[9]Zhang Jing.Compiler Principle[M].Harbin: Harbin Engineering University Press,2011.
[10]Jiang Li-yuan,Kang Mu-Ning.Compiler Principle (3rdEdition)[M].Xi An: Northwestern University Press,2005.
[11]Yan Wei-min,Wu Wei-min.Data Structure Using C[M].Beijng:Tsinghua University Press,2012.
[12]J.R.Bell.A New Method for Determining Linear Precedence Functions for Precedence Grammars.CACM,1969,12:567-569.
[13]D.E.Martin.A Boolean Matrix Method for the Computation of Linear Precedence Functions.CACM,1972,15:448-454.
[14]C.Duong-Kien, H.J.Hoffman, D.Muth[J].A improvement to Martin's algorithm for computation of linear precedence functions,CACM, 1976,19(10): 576-577.
[15]Violetta Lonati,Dino Mandrioli,and Matteo Pradella.Precedence Automata and Languages[J].CSR 2011,LNCS 6651,2011,291-304.
[16]Stefano Crespi Reghizzi, Dino Mandrioli.Operator Precedence and the Visibly Pushdown Automata[J].J.Computer and System Sciences, 2012,78:1837-1867.
[17]Rajeev Alur,P.Madhusudan.Visibly Pushdown Language[M].In STOC: ACM Symposium on Theory of Computing, STOC 2004.
