Al体弹性模量与压强关系的嵌入原子模型研究

朱湘萍 廖树帜

(1.湖南科技学院 电子工程系，湖南 永州 425199；2.湖南师范大学 物理系，湖南 长沙 410081)

1 引 言

随着计算材料学的发展以及高性能计算机的出现，采用理论计算方法开发和设计新型材料已成为材料研发的重要手段之一[1]。由于金属铝具有轻量化、再生利用等优点，轻质铝材料及其合金已成为现代材料工程领域，特别是汽车工业、航空航天工业中不可缺少的结构材料[2-4]。体弹性模量是金属材料性能的一个重要指标，影响金属的体弹性模量的因素比较多，其中压强在一定程度上制约了铝及铝合金在相关领域的应用，所以，深入研究压强对金属铝体弹性模量的影响，在材料的应用等方面具有重要的实际意义。

上世纪80年代中期，Daw 和Baskes提出了一种嵌入原子方法(Embedded Atom Method，简称EAM)模型，主要应用于计算固体中原子总能量[5]。但这种模型计算比较复杂，难推广应用，于是Johnson 采用最近邻嵌入原子方法，提出分析型嵌入原子方法(AEAM)理论[6-7]。为了更好描述金属以及其合金的性能，张邦维等提出了改进分析型嵌入原子方法(MAEAM)理论[8-10]。文献[11]利用嵌入原子模型理论，考虑了压强效应，推导出体心立方体铁的体弹性模量与压强的关系，突出了MAEAM理论在一定条件下的合理性和优越性。本文用改进分析型嵌入原子方法，结合非简谐理论，进行一些近似处理，推导出面心立方体金属铝的体弹性模量与压强的关系，为铝和铝合金的应用提供一个参考依据。

2 理论模型

2.1 基于MAEAM模型金属铝总势能函数的表达式

基于MAEAM模型，采用经典的处理方法，假设面心立方体金属铝由N个原子组成，那么每个原子的平均嵌入原子势可表示如下：

至于参数a、b、c、d和e的值采用张邦维提出的方法确定[9]。考虑平均嵌入原子势φ （r）随两原子的间距r增大而按指数规律迅速衰减，对于面心立方结构的金属Al的总势能，只要虑近邻的前四项，嵌入原子势就比较精确了，如果用R表示面心立方体晶体中两原子的最短距离，则式(1)可写为：

假设金属铝是由N个原子组成的，基于MAEAM模型，则金属铝的总嵌入原子势可以表示如下：

2.2 简谐系数和非简谐系数

设面心立方结构金属Al的体系是由N个原子组成，当晶体平衡后，设R0为两原子间的间距，将原子的平均嵌入原子势φ （R）在平衡点R0附近展开，即有

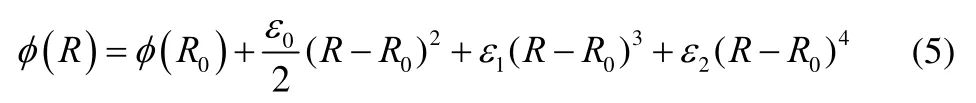
对于势函数的相关系数：简谐系数为0ε、第一非简谐系数为1ε、第二非简谐系数2ε，并可以通过以下式子求出相应的值：

3 结果和讨论

3.1 简谐系数和非简谐系数的计算

金属Al的MAEAM势参数值[9]：a=3.348，b=2.6733，c=0.4025，d=1.7087103，e=3.348数据，代入（3），再把结果分别代入（6）、（7）和（8）式，得到：

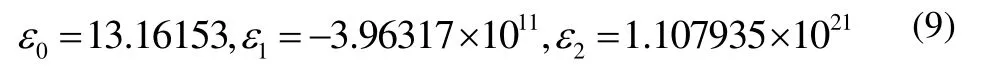
3.2 金属Al的体弹性模量随压强的变化

面心立方(FCC)结构金属Al，晶体体积为：

于是得到压强P和体弹性模量B分别为：

对于FCC结构金属：

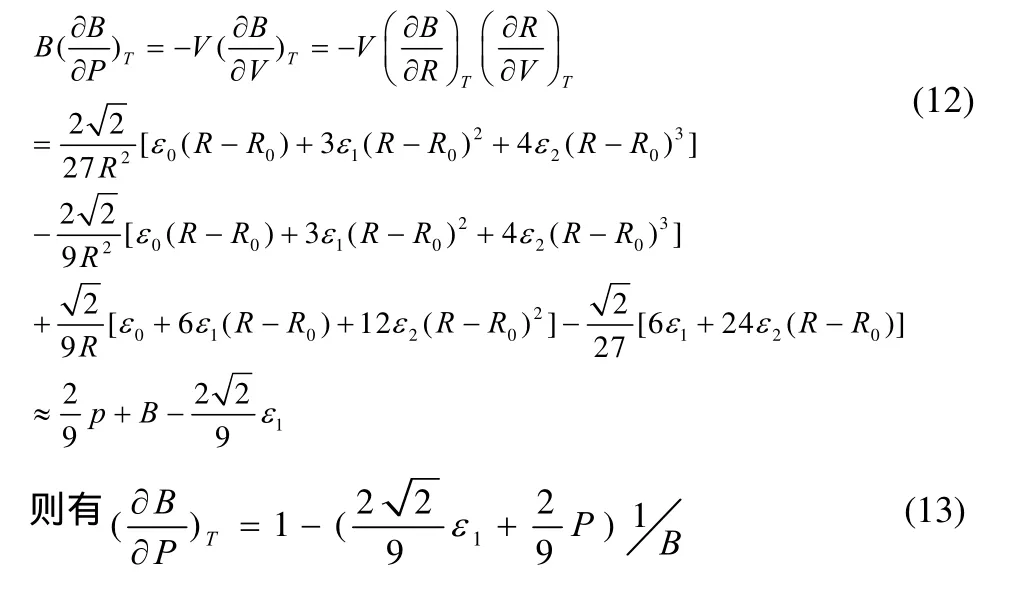
这就是面心立方结构金属的体弹性模量与压强满足的微分关系式。一般情况洗，金属的体弹性模量的数量级约为1011N/m2，就算压强的大小为一万个大气压，其值约为109N/m2，远远比金属的体弹性模量的值小，所以（13）式括号中第二项可以忽略，当采用零级近似处理后，把结果代入（13）式的右端，可得（13）式一级近似解为：

其中B0为P=0时的体弹性模量,将（3）式代入（4）式，将结果代入（14）式得到求得面心立方结构金属Al压强为零时的体弹性模量B0=0.802Mbar，于是得到FCC结构金属铝的体弹性模量随压强变化的规律：

为了形象描述金属铝的体弹性模量随压强的关系，采用了Origin软件，作出了图1，其中用五角星表示曲线是本文基于MAEAM模型下推导的金属铝的体弹性模量与压强的关系曲线，方便比较，在同一坐标上也作出了其它势模型下理论值和实验值。

图1.Al体弹性模量B随压强P的变化

3.3 分析与讨论

（1）在一定条件下，压强会影响金属铝和铝合金的体弹性模量。当压强比较小时，压强增大，金属铝的体弹性模量几乎不变，当压强比较大时，由于受到第一非简谐系数的影响，压强增大，金属铝的弹性模量也增大。解释如下：低压时，压强对晶体的体积变化小，几乎接近0，所以低压情况时，压强对金属铝的体弹性模量影响比较小，几乎没变化；由于金属的弹性模量的大小主要决定于金属的自排斥力大小，当压强比较大时，自排力比较大，所以体弹性模量就比较大[19]。

（2）探讨铝金属的体弹性模量影响因素时，需要考虑非简谐效应的影响，且所构建的MAEAM模型在一定条件下是比较合理且可行的。主要体现于：首先金属铝的在零温度零压强的条件，跟实验测量数据[13]和其他模型下推导的结果[14-18]几乎吻合；其次当压强 P＜100Gpa时与理论结果吻合很好文献[12]；再次，采用经典的方法，通过一级近似处理时，只有第一非简谐系数影响金属铝的体弹性模量随压强的变化。

4 结 论

(1)在推导金属铝的体弹性模量与压强变化规律时，所构建的MAEAM模型是合理可行的，特别是结合非简谐理论时，所推导的结果相对而言，更能准确地反映铝的体弹性模量受压强的影响程度。

(2)在一定条件下，压强对金属及其合金的体弹性模量具有一定的影响，主要因素是第一非简谐系数，至于简谐系数和第二非简谐系数，它们对金属及其合金的体弹性模量随压强的变化规律无影响，考虑非简谐振动后的金属及其合金的体弹性模量大于不考虑时的相应值[11]。

(3)构建任何一种势模型，都具有一定的局限性。比如要具体计算某材料的体弹性模量，根据实际条件和实际需要，选择合适的势模型。

[1]代建红.Al 基 Mg 基和 Ti 基合金相稳定性与弹性性质的第一性原理研究[D].哈尔滨:哈尔滨工业大学,2013.

[2]沈保罗.铸造铝基复合材料在汽车工业中的应用[J].稀有金属材料与工程, 1996, 25(6): 46-49.

[3]李猛进,孙晓峰,管恒,等.Pd-Ni-Al 涂层的抗高温循环氧化性能[J].稀有金属材料与工程, 2004, 33(4): 429-403.

[4]迟广俊,范君,姚素薇.抗菌功能性铝基材料的制备及表征[J].稀有金属材料与工程, 2006, 35(4): 659-661

[5]Daw M S, Baske M I.Embedded-Atom Method: Derivation and Application to Impurities, Surfaces, and other Defects in Metals [J].Phys.Rev.B, 1984, 29(12): 6443-6453.

[6]Johnson R.A.Analytic Nearest-Neighbor Model for fcc Metals[J].Phys.Rev.B, 1988, 37(8): 3924-3931.

[7]Johnson R A.Phase Stability of fcc Alloys with the Embedded-Atom Method [J].Phys.Rev.B, 1990, 41(14):9717-9720.

[8]Zhang Bangwei, Ouyang.Yifang.Theoretical Calculation of Thermodynamic Data for bcc Binary Alloys with the Embedded-Atom Method [J].Phys.Rev.B, 1993, 48(5):3022- 3029.

[9]张邦维,胡望宇,舒小林.嵌入原子方法理论及其在材料科学中的应用) [M].长沙:湖南大学,2002, 245-256.

[10]Hu Wangyu, Zhang Bangwei, Huang Baiyun, et al.Analytic modified embedded atom potentials for HCP metals[J].J.Phys.: Condens.Matter, 2001, 13: 1193-1213.

[11]朱湘萍,刘宏贵,廖树帜.金属 Fe体弹性模量与压强关系的嵌入原子模型研究[J].湖南科技学院学报,2008,29(8):20-22.

[12]姬广富.从头算方法研究面心立方铝在高温高压下的热力学状态方程[J].物理学报,2009,58(6):41003-41008.

[13]Greene R G, Luo H, Ruoff.Al as a Simple Solid: High Pressure Study to 220 GPa (2.2 Mbar) [J].Phys.Rev.Lett.1994:732075.

[14]Girifalco L A, Weizer V G.Application of the Morse Potential Function to Cubic Metals [J].Phys.Rev.B, 1959,114(3): 678-690.

[15]Thakur K P.Mechanical Behaviour of FCC and BCC Metals and Their Stability under Hydrostatic Compressive and Tensile Stresses [J].J.Phys.F: Met.Phys., 1985, 15:2421~2443.

[16]Gaudoin R, Foulkes W M C, Rajagopal G.Ab initio Calculations of the Cohesive Energy and the Bulk Modulus of Aluminium [J].J.Phys.: Condens.Matter.,2002,14:8787-8793.

[17]Bercegeay C, Bernard S.First-Principles Equations of State and Elastic Properties of Seven Metals [J].Phys.Rev.B,2005, 72(21): 214101~1-9.

[18]Milstein F, Huang K.Existence of a Negative Poisson Ratio in fcc Crystals [J].Phys.Rev.B, 1979, 19(4):2030-2033.

[19]黄昆.固体物理学[M].北京:高等教育出版社,2004: 51-54.